Zagadnienia

6.1 Przejścia w dół przez przedział
6.2 Zbieżność prawie na pewno
6.3 Jednostajna całkowalność
6.4 Ciągła wersja twierdzenia Dooba
6.5 Zbieżność martyngałów w $L_{p}$
6.6 Uwagi i uzupełnienia
6.7 Zadania

6. Twierdzenia o zbieżności martyngałów

Udowodnimy twierdzenia o zbieżności martyngałów z czasem ciągłym prawie na pewno i w $L_{p}$ . Wykażemy też ciągłą wersję twierdzenia Dooba ,,optional sampling”.

6.1. Przejścia w dół przez przedział

Definicja 6.1

Załóżmy, że $I\subset{\mathbb{R}}$ , $f\colon I\rightarrow{\mathbb{R}}$ oraz $\alpha<\beta$ . Jeśli $I$ jest skończone, to określamy

$\tau _{{1}}:=\inf\{ t\in I\colon f(t)\geq\beta\}\mbox{ oraz }\sigma _{{1}}:=\inf\{ t\in I\colon t>\tau _{{1}},f(t)\leq\alpha\}$

i dalej indukcyjnie dla $i=1,2,\ldots$

$\tau _{{i+1}}:=\inf\{ t\in I\colon t>\sigma _{{i}},f(t)\geq\beta\}\mbox{ oraz }\sigma _{{i+1}}:=\inf\{ t\in I\colon t>\tau _{{i+1}},f(t)\leq\alpha\}.$

Definiujemy

$D_{{I}}(f,[\alpha,\beta]):=\sup\{ j\colon\sigma _{{j}}<\infty\}\vee 0.$

W przypadku, gdy $I$ jest nieskończone kładziemy

$D_{{I}}(f,[\alpha,\beta]):=\sup\{ D_{{F}}(f,[\alpha,\beta])\colon F\subset T\mbox{ skończone}\}.$

Wielkość $D_{{I}}(f,[\alpha,\beta])$ nazywamy liczbą przejść w dół funkcji $f$ przez przedział $[\alpha,\beta]$ .

Przypomnijmy fakt z rachunku prawdopodobieństwa wiążący skończoność liczby przejść ciągu przez przedział z istnieniem granicy.

Lemat 6.1

Ciąg liczbowy $x_{{n}}$ jest zbieżny do pewnej, niekoniecznie skończonej granicy wtedy i tylko wtedy, gdy $D_{{{\mathbb{N}}}}((x_{{n}}),[\alpha,\beta])<\infty$ dla dowolnych liczb wymiernych $\alpha<\beta$ .

Następny lemat jest niewielką modyfikacją poprzedniego.

Lemat 6.2

Jeśli $f\colon[a,b)\rightarrow{\mathbb{R}}$ , $b\leq\infty$ jest prawostronnie ciągłą funkcją taką, że dla dowolnych liczb wymiernych $\alpha<\beta$ , $D_{{[a,b)\cap{\mathbb{Q}}}}(f,[\alpha,\beta])<\infty$ , to istnieje (niekoniecznie skończona) granica $\lim _{{t\rightarrow b}}f(t)$ .

Załóżmy, że postulowana granica nie istnieje, wtedy można znaleźć liczby wymierne $\alpha,\beta$ takie, że

$\liminf _{{t\rightarrow b}}f(t)<\alpha<\beta<\limsup _{{t\rightarrow b}}f(t).$

Stąd wynika, że istnieje rosnący ciąg liczb wymiernych $t_{n}$ z przedziału $[a,b)$ taki, że $f(t_{{2k-1}})\geq\beta$ oraz $f(t_{{2k}})\leq\alpha$ . Przyjmując $I=\{ t_{1},t_{2},\ldots\}$ widzimy, że $D_{{[a,b)\cap{\mathbb{Q}}}}(f,[\alpha,\beta])\geq D_{{I}}(f,[\alpha,\beta])=\infty$ .

∎

Lemat 6.3

Załóżmy, że $X=(X_{{t}})_{{t\in T}}$ jest podmartyngałem względem pewnej filtracji, a $F$ jest przeliczalnym podzbiorem $T$ , wówczas

${\mathbb{E}}D_{{F}}(X,[\alpha,\beta])\leq\sup _{{t\in F}}\frac{{\mathbb{E}}(X_{{t}}-\beta)^{{+}}}{\beta-\alpha}.$

Stosując twierdzenie Lebesgue'a o zbieżności monotonicznej widzimy, że wystarczy udowodnić lemat dla skończonych zbiorów $F$ , dla uproszczenia notacji możemy oczywiście przyjąć, że $F=\{ 1,2,\ldots,N\}$ . Zauważmy, że (przy oznaczeniach jak w Definicji 6.1)

$X_{{\tau _{{i}}\wedge N}}-X_{{\sigma _{{i}}\wedge N}}=\left\{\begin{array}[]{ll}X_{{\tau _{{i}}}}-X_{{\sigma _{{i}}}}\geq\beta-\alpha&\mbox{ gdy }\sigma _{{i}}<\infty,\\ X_{{\tau _{{i}}}}-X_{{N}}\geq\beta-X_{{N}}\geq-(X_{{N}}-\beta)^{{+}}&\mbox{ gdy }\tau _{{i}}<\sigma _{i}=\infty,\\ X_{{N}}-X_{{N}}=0&\mbox{ gdy }\tau _{{i}}=\infty.\end{array}\right.$

Zatem

$\sum _{{i=1}}^{{N}}(X_{{\tau _{{i}}\wedge N}}-X_{{\sigma _{{i}}\wedge N}})\geq(\beta-\alpha)D_{{F}}(X,[\alpha,\beta])-(X_{{N}}-\beta)^{{+}}.$

Na mocy Lematu 5.1, ${\mathbb{E}}X_{{\tau _{{i\wedge N}}}}\leq{\mathbb{E}}X_{{\sigma _{{i\wedge N}}}}$ , więc

$0\geq{\mathbb{E}}\sum _{{i=1}}^{{N}}(X_{{\tau _{{i}}\wedge N}}-X_{{\sigma _{{i}}\wedge N}})\geq{\mathbb{E}}(\beta-\alpha)D_{{F}}(X,[\alpha,\beta])-{\mathbb{E}}(X_{{N}}-\beta)^{{+}}.$

∎

6.2. Zbieżność prawie na pewno

Przypomnijmy twierdzenie dotyczące zbieżności podmartyngałów z czasem dyskretnym:

Twierdzenie 6.1

Załóżmy, że $(X_{{n}})_{{n\in{\mathbb{N}}}}$ jest podmartyngałem względem pewnej filtracji takim, że $\sup _{{n\in{\mathbb{N}}}}{\mathbb{E}}X_{{n}}^{{+}}<\infty$ (lub nadmartyngałem takim, że $\sup _{{n\in{\mathbb{N}}}}{\mathbb{E}}X_{{n}}^{{-}}<\infty$ ), wówczas $X=\lim _{{n\rightarrow\infty}}X_{{n}}$ istnieje i jest skończona p.n., ponadto ${\mathbb{E}}|X|<\infty$ .

Sformułujemy teraz odpowiednik powyższego twierdzenia dla czasu ciągłego.

Twierdzenie 6.2

Załóżmy, że $(X_{{t}})_{{t\in[a,b)}}$ , $b\leq\infty$ jest podmartyngałem o prawostronnie ciągłych trajektoriach takim, że $\sup _{{t\in[a,b)}}{\mathbb{E}}X_{{t}}^{{+}}<\infty$ . Wówczas $X=\lim _{{t\rightarrow b}}X_{{t}}$ istnieje i jest skończony p.n., ponadto ${\mathbb{E}}|X|<\infty$ .

Dla ustalonego $\alpha<\beta$ na podstawie Lematu 6.3 mamy

${\mathbb{E}}D_{{[a,b)\cap{\mathbb{Q}}}}(X_{{t}},[\alpha,\beta])\leq\frac{1}{\beta-\alpha}\sup _{{t\in[a,b)}}{\mathbb{E}}(X_{{t}}-\beta)^{{+}}<\infty,$

zatem ${\mathbb{P}}(D_{{[a,b)\cap{\mathbb{Q}}}}(X_{{t}},[\alpha,\beta])=\infty)=0$ . Niech

$A:=\bigcap _{{\alpha,\beta\in{\mathbb{Q}},\alpha<\beta}}\{ D_{{[a,b)\cap{\mathbb{Q}}}}(X_{{t}},[\alpha,\beta])<\infty\},$

wówczas ${\mathbb{P}}(A)=1$ , bo $A$ jest przecięciem przeliczalnej liczby zbiorów pełnej miary. Jeśli $\omega\in A$ , to $D_{{[a,b)\cap{\mathbb{Q}}}}(X_{{t}}(\omega),[\alpha,\beta])<\infty$ dla dowolnych liczb wymiernych $\alpha<\beta$ , czyli, na podstawie Lematu 6.2, granica $X(\omega):=\lim _{{t\rightarrow b}}X_{{t}}(\omega)$ istnieje (choć apriori może być nieskończona). Zauważmy, że ${\mathbb{E}}|X_{{t}}|=2{\mathbb{E}}X_{{t}}^{{+}}-{\mathbb{E}}X_{{t}}\leq 2{\mathbb{E}}X_{{t}}^{{+}}-{\mathbb{E}}X_{{0}}$ , zatem $\sup _{{t\in[a,b)}}{\mathbb{E}}|X_{{t}}|<\infty$ . Z Lematu Fatou

${\mathbb{E}}|X|={\mathbb{E}}\lim _{{t\rightarrow b}}|X_{{t}}|\leq\liminf _{{t\rightarrow b}}{\mathbb{E}}|X_{{t}}|\leq\sup _{{t}}{\mathbb{E}}|X_{{t}}|<\infty,$

czyli zmienna $X$ jest całkowalna, a więc w szczególności skończona p.n..

∎

Wniosek 6.1

Załóżmy, że $(X_{{t}})_{{t\geq 0}}$ jest niedodatnim podmartyngałem (lub nieujemnym nadmartyngałem) o prawostronnie ciągłych trajektoriach, wówczas granica $X=\lim _{{t\rightarrow\infty}}X_{{t}}$ istnieje i jest skończona p.n., ponadto ${\mathbb{E}}|X|<\infty$ .

6.3. Jednostajna całkowalność

Definicja 6.2

Rodzinę zmiennych losowych $(X_{{i}})_{{i\in I}}$ nazywamy jednostajnie całkowalną, jeśli

$\lim _{{C\rightarrow\infty}}\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{\{|X_{{i}}|>C\}}}=0.$

Stwierdzenie 6.1

Rodzina zmiennych losowych $(X_{{i}})_{{i\in I}}$ jest jednostajnie całkowalna wtedy i tylko wtedy, gdy spełnione są następujące dwa warunki
a) $\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|<\infty$ ,
b) $\forall _{{\varepsilon>0}}\exists _{{\delta>0}}\ {\mathbb{P}}(A)\leq\delta\Rightarrow\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{A}}\leq\varepsilon$ .

$\Rightarrow$ : Ustalmy $\varepsilon>0$ i dobierzmy $C$ takie, że $\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{\{|X_{{i}}|>C\}}}\leq\varepsilon/2$ . Wówczas

$\forall _{{i\in I}}\ {\mathbb{E}}|X_{{i}}|\leq C+{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{\{|X_{{i}}|>C\}}}\leq C+\varepsilon/2<\infty$

oraz, jeśli ${\mathbb{P}}(A)<\delta:=\frac{\varepsilon}{2C}$ , to

${\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{A}}\leq C{\mathbb{P}}(A)+{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{\{|X_{{i}}|>C\}}}\leq C\delta+\frac{\varepsilon}{2}=\varepsilon.$

$\Leftarrow$ : Niech $\alpha:=\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|$ oraz $\delta>0$ będzie takie, że $\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{A}}\leq\varepsilon$ dla ${\mathbb{P}}(A)\leq\delta$ . Wówczas, jeśli $C=\alpha/\delta$ , to ${\mathbb{P}}(|X_{{i}}|>C)<\alpha/C=\delta$ dla dowolnego $i\in I$ , czyli $\sup _{{i\in I}}{\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{\{|X_{{i}}|>C\}}}\leq\varepsilon$ .

∎

Podamy teraz kilka przykładów rodzin jednostajnie całkowalnych.

Przykład 6.1

Rodzina jednoelementowa $\{ Y\}$ taka, że ${\mathbb{E}}|Y|<\infty$ .

Istotnie, na mocy twierdzenia Lebesgue'a o zbieżności zmajoryzowanej mamy $\lim _{{C\rightarrow\infty}}{\mathbb{E}}|Y|{\mathrm{I}}_{{\{|Y|>C\}}}=0$ .

Przykład 6.2

Rodzina wspólnie ograniczona przez zmienną całkowalną tzn. rodzina $(X_{{i}})_{{i\in I}}$ taka, że $\forall _{{i\in I}}|X_{{i}}|\leq Y$ oraz ${\mathbb{E}}Y<\infty$ .

Wynika to ze Stwierdzenia 6.1, poprzedniego przykładu i oczywistej obserwacji ${\mathbb{E}}|X_{{i}}|{\mathrm{I}}_{{A}}\leq{\mathbb{E}}|Y|{\mathrm{I}}_{{A}}$ .

Przykład 6.3

Rodzina uśrednień ustalonej całkowalnej zmiennej losowej, tzn. rodzina postaci $({\mathbb{E}}(X|{\mathcal{F}}_{{i}}))_{{i\in I}}$ , gdzie ${\mathbb{E}}|X|<\infty$ , zaś $({\mathcal{F}}_{{i}})_{{i\in I}}$ dowolna rodzina $\sigma$ -podciał ${\mathcal{F}}$ .

Na podstawie nierówności Jensena ${\mathbb{E}}|X_{{i}}|={\mathbb{E}}|{\mathbb{E}}(X|{\mathcal{F}}_{{i}})|\leq{\mathbb{E}}|X|$ , a zatem

${\mathbb{P}}(|X_{{i}}|\geq C)\leq\frac{{\mathbb{E}}|X_{{i}}|}{C}\leq\frac{{\mathbb{E}}|X|}{C}\leq\delta\quad\mbox{dla }C\geq\frac{{\mathbb{E}}|X|}{\delta}.$

Zbiór $\{|X_{{i}}|>C\}\in{\mathcal{F}}_{{i}}$ , więc z nierówności Jensena

	$\displaystyle{\mathbb{E}}\|X_{{i}}\|{\mathrm{I}}_{{\{\|X_{{i}}\|>C\}}}$	$\displaystyle={\mathbb{E}}\|{\mathbb{E}}(X{\mathrm{I}}_{{\{\|X_{{i}}\|>C\}}}\|{\mathcal{F}}_{{i}})\|\leq{\mathbb{E}}{\mathbb{E}}(\|X\|{\mathrm{I}}_{{\{\|X_{{i}}\|>C\}}}\|{\mathcal{F}}_{{i}})$
		$\displaystyle\leq{\mathbb{E}}(\|X\|{\mathrm{I}}_{{\{\|X_{{i}}\|>C\}}})\leq\varepsilon,$

jeśli tylko dobierzemy odpowiednio małe $\delta$ korzystając z jednostajnej całkowalności $\{|X|\}$ .

Jednostajna całkowalność jest jednym z kluczowych narzędzi (obok twierdzenia o zbieżności zmajoryzowanej) pozwalającym ze zbieżności prawie na pewno wywnioskować zbieżność w $L_{p}$ .

Stwierdzenie 6.2

Załóżmy, że $1\leq p<\infty$ , a $X_{{n}}$ są zmiennymi losowymi takimi, że rodzina $(|X_{{n}}|^{{p}})_{{n=1}}^{{\infty}}$ jest jednostajnie całkowalna. Wówczas $X_{{n}}$ zbiega do zmiennej $X$ w $L_{{p}}$ wtedy i tylko wtedy, gdy $X_{{n}}$ zbiega do $X$ według prawdopodobieństwa.

Wystarczy udowodnić, że zbieżność $X_{{n}}$ według prawdopodobieństwa implikuje zbieżność w $L_{{p}}$ , bo przeciwna implikacja jest zawsze prawdziwa. Załóżmy więc, że $X_{{n}}\overset{{\mathbb{P}}}{\rightarrow}X$ , wówczas dla pewnego podciągu $n_{{k}}$ , $X_{{n_{{k}}}}$ zbiega do $X$ p.n., stąd na mocy Lematu Fatou

${\mathbb{E}}|X|^{{p}}={\mathbb{E}}\lim _{{k\rightarrow\infty}}|X_{{n_{{k}}}}|^{{p}}\leq\liminf _{{k\rightarrow\infty}}{\mathbb{E}}|X_{{n_{{k}}}}|^{{p}}\leq\sup _{{n}}{\mathbb{E}}|X_{{n}}|^{{p}}<\infty.$

Zatem rodzina $\{|X_{{n}}|^{{p}}\colon n=1,2,\ldots\}\cup\{|X|^{{p}}\}$ jest jednostajnie całkowalna. Ustalmy $\varepsilon>0$ i dobierzmy $\delta>0$ tak, by dla ${\mathbb{P}}(A)<\delta$ zachodziło ${\mathbb{E}}|X_{{n}}|^{{p}}{\mathrm{I}}_{{A}}\leq\varepsilon$ oraz ${\mathbb{E}}|X|^{{p}}{\mathrm{I}}_{{A}}\leq\varepsilon$ . Mamy

	$\displaystyle{\mathbb{E}}\|X_{{n}}-X\|^{{p}}$	$\displaystyle\leq\varepsilon^{{p}}+{\mathbb{E}}\|X_{{n}}-X\|^{{p}}{\mathrm{I}}_{{\{\|X_{{n}}-X\|>\varepsilon\}}}$
		$\displaystyle\leq\varepsilon^{{p}}+2^{{p}}{\mathbb{E}}\|X_{{n}}\|^{{p}}{\mathrm{I}}_{{\{\|X_{{n}}-X\|>\varepsilon\}}}+2^{{p}}{\mathbb{E}}\|X\|^{{p}}{\mathrm{I}}_{{\{\|X_{{n}}-X\|>\varepsilon\}}},$

a ponieważ $X_{{n}}\overset{{\mathbb{P}}}{\rightarrow}X$ , więc ${\mathbb{P}}(|X_{{n}}-X|>\varepsilon)<\delta$ dla dużych $n$ , czyli

${\mathbb{E}}|X_{{n}}-X|^{{p}}\leq\varepsilon^{{p}}+2^{{p+1}}\varepsilon\mbox{ dla dostatecznie dużych }n.$

∎

Wniosek 6.2

Jeśli rodzina $(X_{{n}})_{{n=1}}^{{\infty}}$ jest jednostajnie całkowalna oraz $X_{{n}}$ zbiega prawie na pewno do zmiennej $X$ , to $\lim _{{n\rightarrow\infty}}{\mathbb{E}}X_{{n}}{\mathrm{I}}_{{A}}={\mathbb{E}}X{\mathrm{I}}_{{A}}$ dla wszystkich zdarzeń $A$ .

Stosujemy Stwierdzenie 6.2 i oczywiste szacowanie $|{\mathbb{E}}X_{{n}}{\mathrm{I}}_{{A}}-{\mathbb{E}}X{\mathrm{I}}_{{A}}|\leq{\mathbb{E}}|X_{{n}}-X|$ .

∎

6.4. Ciągła wersja twierdzenia Dooba

Jesteśmy teraz gotowi do dowodu ciągłej wersji Lematu 5.1.

Twierdzenie 6.3

a) Załóżmy, że $T$ jest przedziałem, a $(X_{{t}})_{{t\in T}}$ martyngałem prawostronnie ciągłym, zaś $\sigma$ i $\tau$ czasami zatrzymania takimi, że $\sigma\leq\tau\leq t_{{\max}}$ oraz $t_{{\max}}\in T$ . Wówczas ${\mathbb{E}}(X_{{\tau}}|{\mathcal{F}}_{{\sigma}})=X_{{\sigma}}$ p.n..
b) Jeśli $(X_{{t}})_{{0\leq t\leq\infty}}$ jest prawostronnie ciągłym martyngałem z ostatnim elementem $X_{{\infty}}$ to dla dowolnych dwu czasów zatrzymania $\sigma\leq\tau$ , ${\mathbb{E}}(X_{{\tau}}|{\mathcal{F}}_{{\sigma}})=X_{{\sigma}}$ p.n.

Udowodnimy część a) (część b) można za pomocą zmiany czasu sprowadzić do a)). Zdefiniujmy

$\tau _{{n}}(\omega):=\left\{\begin{array}[]{ll}t_{{\max}}-\frac{k}{n}&\mbox{ dla }\tau(\omega)\in(t_{{\max}}-\frac{k+1}{n},t_{{\max}}-\frac{k}{n}],k=0,1,\ldots,n^{{2}},\\ t_{{\max}}-n&\mbox{ dla }\tau(\omega)\leq t_{{\max}}-n\end{array}\right.$

oraz

$\sigma _{{n}}(\omega):=\left\{\begin{array}[]{ll}t_{{\max}}-\frac{k}{n}&\mbox{ dla }\sigma(\omega)\in(t_{{\max}}-\frac{k+1}{n},t_{{\max}}-\frac{k}{n}],k=0,1,\ldots,n^{{2}},\\ t_{{\max}}-n&\mbox{ dla }\sigma(\omega)\leq t_{{\max}}-n.\end{array}\right.$

Wówczas $\sigma _{{n}}\leq\tau _{{n}}\leq t_{{\max}}$ są ograniczonymi czasami zatrzymania przyjmującymi jedynie skończenie wiele wartości. Zatem na mocy Lematu 5.1 mamy ${\mathbb{E}}(X_{{\tau _{{n}}}}|{\mathcal{F}}_{{\sigma _{{n}}}})=X_{{\sigma _{{n}}}}$ p.n., ${\mathbb{E}}(X_{{t_{{\max}}}}|{\mathcal{F}}_{{\sigma _{{n}}}})=X_{{\sigma _{{n}}}}$ p.n. oraz ${\mathbb{E}}(X_{{t_{{\max}}}}|{\mathcal{F}}_{{\tau _{{n}}}})=X_{{\tau _{{n}}}}$ p.n., w szczególności więc rodziny $(X_{{\tau _{{n}}}})_{{n=1}}^{{\infty}}$ oraz $(X_{{\sigma _{{n}}}})_{{n=1}}^{{\infty}}$ są jednostajnie całkowalne. Ponieważ $\tau _{{n}}\rightarrow\tau+$ oraz $\sigma _{{n}}\rightarrow\sigma+$ , więc z prawostronnej ciągłości $X$ oraz Stwierdzenia 6.2, $X_{{\tau _{{n}}}}\rightarrow X_{{\tau}}$ , $X_{{\sigma _{{n}}}}\rightarrow X_{{\sigma}}$ p.n. i w $L_{{1}}$ . Weźmy $A\in{\mathcal{F}}_{{\sigma}}\subset{\mathcal{F}}_{{\sigma _{{n}}}}$ , wówczas

${\mathbb{E}}X_{{\tau}}{\mathrm{I}}_{{A}}=\lim _{{n\rightarrow\infty}}{\mathbb{E}}X_{{\tau _{{n}}}}{\mathrm{I}}_{{A}}=\lim _{{n\rightarrow\infty}}{\mathbb{E}}X_{{\sigma _{{n}}}}{\mathrm{I}}_{{A}}={\mathbb{E}}X_{{\sigma}}{\mathrm{I}}_{{A}},$

co oznacza, że ${\mathbb{E}}(X_{{\tau}}|{\mathcal{F}}_{{\sigma}})=X_{{\sigma}}$ p.n..

∎

Wniosek 6.3

Załóżmy, że $T$ jest przedziałem, a $(M_{t})_{{t\in T}}$ jest prawostronnie ciągłym martyngałem względem $({\mathcal{F}}_{t})_{{t\in T}}$ . Wówczas dla dowolnego momentu zatrzymania $\tau$ proces $M^{{\tau}}=(M_{{\tau\wedge t}})_{{t\in T}}$ jest martyngałem zarówno względem $({\mathcal{F}}_{{\tau\wedge t}})_{{t\in T}}$ , jak i $({\mathcal{F}}_{t})_{{t\in T}}$ .

Niech $s<t$ oraz $s,t\in T$ , wówczas $\tau\wedge s\leq\tau\wedge t\leq t$ , więc z Twierdzenia 6.3 mamy ${\mathbb{E}}(M_{{\tau\wedge t}}|{\mathcal{F}}_{{\tau\wedge s}})=M_{{\tau\wedge s}}$ p.n., czyli $(M_{{\tau\wedge t}},{\mathcal{F}}_{{\tau\wedge t}})_{{t\in T}}$ jest martyngałem.

By udowodnić drugą część ustalmy $s<t$ oraz $A\in{\mathcal{F}}_{s}$ . Nietrudno sprawdzić, że $A\cap\{\tau>s\}\in{\mathcal{F}}_{{\tau\wedge s}}$ , zatem z poprzednio udowodnionej części wniosku mamy

${\mathbb{E}}M_{{\tau\wedge t}}{\mathrm{I}}_{{A\cap\{\tau>s\}}}={\mathbb{E}}M_{{\tau\wedge s}}{\mathrm{I}}_{{A\cap\{\tau>s\}}}.$

Ponadto

${\mathbb{E}}M_{{\tau\wedge t}}{\mathrm{I}}_{{A\cap\{\tau\leq s\}}}={\mathbb{E}}M_{{\tau}}{\mathrm{I}}_{{A\cap\{\tau\leq s\}}}={\mathbb{E}}M_{{\tau\wedge s}}{\mathrm{I}}_{{A\cap\{\tau\leq s\}}}.$

Dodając powyższe tożsamości stronami otrzymujemy ${\mathbb{E}}M_{{\tau\wedge t}}{\mathrm{I}}_{{A}}={\mathbb{E}}M_{{\tau\wedge s}}{\mathrm{I}}_{A}$ dla $A\in{\mathcal{F}}_{s}$ , zatem $(M_{{\tau\wedge t}},{\mathcal{F}}_{{t}})_{{t\in T}}$ jest martyngałem.

∎

6.5. Zbieżność martyngałów w 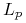$L_{p}$

Zacznijmy od warunków zbieżności martyngałów z czasem ciągłym w $L_{1}$ .

Twierdzenie 6.4

Załóżmy, że $(X_{{t}})_{{t\in[a,b)}}$ , $b\leq\infty$ jest prawostronnie ciągłym martyngałem. Wówczas następujące warunki są równoważne:
a) Rodzina $(X_{{t}})_{{t\in[a,b)}}$ jest jednostajnie całkowalna.
b) Istnieje całkowalna zmienna losowa $X_{{b}}$ taka, że $X_{{t}}$ zbiega do $X_{{b}}$ w $L_{{1}}$ , tzn. $\lim _{{t\rightarrow b}}{\mathbb{E}}|X_{{t}}-X_{{b}}|=0$ .
c) Istnieje całkowalna zmienna losowa $X_{{b}}$ mierzalna względem $\sigma$ -ciała ${\mathcal{F}}_{{b}}:=\sigma(\bigcup _{{t\in[a,b)}}{\mathcal{F}}_{{t}})$ taka, że $X_{{t}}={\mathbb{E}}(X_{{b}}|{\mathcal{F}}_{{t}})$ dla $t\in[a,b)$ .
W przypadku, gdy zachodzą warunki (a)-(c), to $X_{{b}}=\lim _{{t\rightarrow b}}X_{{t}}$ p.n..

a) $\Rightarrow$ b): $X_{{t}}$ jest jednostajnie całkowalny, więc $\sup _{{t}}{\mathbb{E}}|X_{{t}}|<\infty$ , czyli wobec Twierdzenia 6.2 istnieje zmienna całkowalna $X_{{b}}$ taka, że $X_{{t}}\rightarrow X_{{b}}$ p.n. przy $t\rightarrow b$ . Z jednostajnej całkowalności i Lematu 6.2 wynika zbieżność w $L_{{1}}$ .

b) $\Rightarrow$ c): Dla pewnego podciągu $t_{{k}}\rightarrow b$ , $X_{{t_{{k}}}}\rightarrow X_{{b}}$ p.n., stąd możemy zakładać, że zmienna $X_{{b}}$ jest ${\mathcal{F}}_{{b}}$ mierzalna. Ustalmy $t$ i $A\in{\mathcal{F}}_{{t}}$ , wówczas dla $s\geq t$

${\mathbb{E}}X_{{t}}{\mathrm{I}}_{{A}}={\mathbb{E}}X_{{s}}{\mathrm{I}}_{{A}}\rightarrow{\mathbb{E}}X_{{b}}{\mathrm{I}}_{{A}},\ s\rightarrow\infty.$

Zatem $X_{{t}}={\mathbb{E}}(X_{{b}}|{\mathcal{F}}_{{t}})$ p.n..

c) $\Rightarrow$ a) Wiemy, że rodzina uśrednień ustalonej zmiennej jest jednostajnie całkowalna.

Ostatnia część twiedzenia wynika z dowodu implikacji a) $\Rightarrow$ b).

∎

Twierdzenie 6.5

Załóżmy, że $(X_{{t}})_{{t\in[a,b)}}$ jest prawostronnie ciągłym martyngałem. Wówczas następujące warunki są równoważne:
a) $\sup _{{t\in[a,b)}}{\mathbb{E}}|X_{{t}}|^{{p}}<\infty$ .
b) Rodzina $(|X_{{t}}|^{{p}})_{{t\in[a,b)}}$ jest jednostajnie całkowalna.
c) Istnieje zmienna losowa $X_{{b}}\in L_{{p}}$ taka, że $X_{{t}}$ zbiega do $X_{{b}}$ w $L_{{p}}$ , tzn. $\lim _{{t\rightarrow b}}{\mathbb{E}}|X_{{t}}-X_{{b}}|^{{p}}=0$ .
d) Istnieje zmienna losowa $X_{{b}}\in L_{{p}}$ mierzalna względem ${\mathcal{F}}_{{b}}:=\sigma(\bigcup _{{t\in[a,b)}}{\mathcal{F}}_{{t}})$ taka, że $X_{{t}}={\mathbb{E}}(X_{{b}}|{\mathcal{F}}_{{t}})$ dla $t\in[a,b)$ .
W przypadku, gdy zachodzą warunki (a)-(d), to $X_{{b}}=\lim _{{t\rightarrow b}}X_{{t}}$ p.n..

a) $\Rightarrow$ b): Na podstawie Twierdzenia 5.1 wiemy, że

${\mathbb{E}}\sup _{{t\in[a,b)}}|X_{{t}}|^{{p}}\leq\Big(\frac{p}{p-1}\Big)^{{p}}\sup _{{t\in[a,b)}}{\mathbb{E}}|X_{{t}}|^{{p}}<\infty.$

Pozostałe implikacje dowodzimy jak w dowodzie Twierdzenia 6.4.

∎

6.6. Uwagi i uzupełnienia

W wielu twierdzeniach zakłada się, iż $(X_{t})$ jest prawostronnie ciągłym podmartyngałem. Oczywiście modyfikacja podmartyngału jest podmartyngałem – problem jest tylko z mierzalnością, ale znika on, gdy filtracja spełnia zwykłe warunki. Naturalnie jest więc zapytać kiedy dany podmartyngał możemy zmodyfikować tak, by stał się prawostronnie ciągły. Odpowiedź na to pytanie jest bardzo prosta.

Twierdzenie 6.6

Załóżmy, że $T$ jest przedziałem, a $X=(X_{{t}})_{{t\in T}}$ jest podmartyngałem (odp. nadmartyngałem) względem filtracji $({\mathcal{F}}_{{t}})_{{t\in T}}$ spełniającej zwykłe warunki. Wówczas $X$ ma prawostronnie ciągłą modyfikację wtedy i tylko wtedy, gdy funkcja $t\rightarrow{\mathbb{E}}X_{{t}}$ jest prawostronnie ciągła.

6.7. Zadania

Ćwiczenie 6.1

Które z podanych niżej warunków implikują jednostajną całkowalność ciągu $X_{n}$ :
a) $\sup _{n}{\mathbb{E}}|X_{n}|<\infty$ ,
b) $\sup _{n}{\mathbb{E}}|X_{n}|^{2}<\infty$ ,
c) ${\mathbb{E}}\sup _{n}|X_{n}|<\infty$ ,
d) zbieżność $X_{n}$ w $L_{1}$ ,
e) zbieżność $X_{n}$ p.n.?

Ćwiczenie 6.2

Niech $(X_{n},{\mathcal{F}}_{n})_{{n\leq 0}}$ będzie podmartyngałem (z czasem odwróconym!) takim, że $\lim _{{n\rightarrow-\infty}}{\mathbb{E}}X_{n}>-\infty$ . Wykaż, że $(X_{n})$ jest jednostajnie całkowalny.

Ćwiczenie 6.3

Wykaż, że martyngał $M_{{t}}=\exp(\lambda W_{{t}}-\lambda^{{2}}t/2)$ jest zbieżny p.n. i znajdź jego granicę. Czy jest on zbieżny w $L_{{1}}$ ?

Ćwiczenie 6.4

a) Wykaż, że jeśli $f$ jest dwukrotnie różniczkowalna na ${\mathbb{R}}$ oraz $f,f^{{\prime}},f^{{\prime\prime}}$ są ograniczone, to

$M_{t}=f(W_{t})-f(W_{0})-\frac{1}{2}\int _{{0}}^{t}f^{{\prime\prime}}(W_{u})du$

jest martyngałem względem ${\mathcal{F}}_{t}^{W}$ .
b) Ogólniej, jeśli $f$ jest dwukrotnie różniczkowalna na ${\mathbb{R}}^{d}$ , pochodne cząstkowe $f$ rzędu mniejszego niż 2 są ograniczone oraz $W$ jest $d$ -wymiarowym procesem Wienera, to

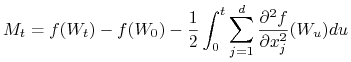$M_{t}=f(W_{t})-f(W_{0})-\frac{1}{2}\int _{{0}}^{t}\sum _{{j=1}}^{d}\frac{\partial^{2}f}{\partial x_{j}^{2}}(W_{u})du$

jest martyngałem względem ${\mathcal{F}}_{t}^{W}$ .

Ćwiczenie 6.5

Niech $\tau$ będzie momentem zatrzymania względem ${\mathcal{F}}_{{t}}^{{W}}$ .
a) Wykaż, że $(W_{{\tau\wedge n}},{\mathcal{F}}_{{\tau\wedge n}})_{{n=1}}^{{\infty}}$ jest martyngałem.
b) Udowodnij, że jeśli ${\mathbb{E}}\tau<\infty$ , to ${\mathbb{E}}\sup _{{n}}W_{{\tau\wedge n}}^{{2}}<\infty$ .
c) Wykaż, że jeśli ${\mathbb{E}}\tau<\infty$ , to ${\mathbb{E}}W_{{\tau}}^{{2}}={\mathbb{E}}\tau$ i ${\mathbb{E}}W_{{\tau}}=0$ .

Ćwiczenie 6.6

Niech $W_{{t}}$ będzie jednowymiarowym procesem Wienera oraz

$\tau _{{a}}:=\inf\{ t>0\colon W_{{t}}=a\},\ \tilde{\tau}_{{a}}:=\inf\{ t>0\colon|W_{{t}}|=a\}.$

Rozpatrując martyngały $W_{{t}}$ i $W_{{t}}^{{2}}-t$ wykaż, że
a) $\tau _{{a}}<\infty$ p.n. dla wszystkich $a\in{\mathbb{R}}$ ,
b) ${\mathbb{P}}(\tau _{{a}}<\tau _{{-b}})=\frac{b}{a+b}$ dla $a,b>0$ ,
c) ${\mathbb{E}}\tilde{\tau}_{{a}}=a^{{2}}$ dla $a\geq 0$ ,
d) ${\mathbb{E}}\tau _{{a}}\wedge\tau _{{-b}}=ab$ dla $a,b>0$ ,
e) ${\mathbb{E}}\tau _{{a}}=\infty$ dla wszystkich $a\neq 0$ .

Ćwiczenie 6.7

Rozpatrując martyngały $M_{{t}}^{{\lambda}}=\exp(\lambda W_{{t}}-\lambda^{{2}}t/2)$ oraz $N_{{t}}^{{\lambda}}=(M_{{t}}^{{\lambda}}+M_{{t}}^{{-\lambda}})/2$ wykaż, że przy oznaczeniach poprzedniego zadania, dla wszystkich $a,\lambda\geq 0$ ,
a) ${\mathbb{E}}e^{{-\lambda\tau _{{a}}}}=e^{{-a\sqrt{2\lambda}}}$ ,
b) ${\mathbb{E}}e^{{-\lambda\tilde{\tau}_{{a}}}}=(\cosh(a\sqrt{2\lambda}))^{{-1}}$ .

Ćwiczenie 6.8

Niech $W_{{t}}=(W_{{t}}^{{1}},\ldots,W_{{t}}^{{d}})$ będzie $d$ wymiarowym procesem Wienera, a $x_{{0}}\in{\mathbb{R}}^{{d}}$ oraz $d>2$ .
a) Wykaż, że $|W_{{t}}-x_{{0}}|^{{2-d}}$ jest nieujemnym nadmartyngałem.
b) Udowodnij, że $|W_{{t}}-x_{{0}}|^{{2-d}}$ zbiega przy $t\rightarrow\infty$ do 0 według prawdopodobieństwa i p.n. oraz wywnioskuj stąd, że $\lim _{{t\rightarrow\infty}}|W_{{t}}|=\infty$ p.n..
c) Wykaż, że dla prawostronnie ciągłego nadmartyngału $(X_{{t}})_{{t\geq a}}$ zachodzi