Zagadnienia
8. Całka izometryczna względem procesu Wienera
Podczas kolejnych wykładów zdefiniujemy całkę względem procesu Wienera - zaczniemy od całkowania funkcji deterministycznych, by później przejść do konstrukcji izometrycznej całki stochastycznej Itô.
Konstrukcja całki stochastycznej ma pewne podobieństwa do konstrukcji całki Lebesgue'a. Najpierw określa się, w naturalny sposób, całki najprostszych funkcji/procesów (funkcje schodkowe, procesy elementarne), później pokazuje się własności tak określonej całki (oparte na liczeniu drugich momentów), które pozwalają uogólnić definicję na bardziej złożone funkcje/procesy.
Należy zwrócić uwagę, że całkę stochastyczną definiujemy globalnie na całej przestrzeni probabilistycznej, a nie dla każdej trajektorii z osobna.
Dla uproszczenia notacji będziemy definiowali całki ![]() . Całkę
. Całkę ![]() dla
dla ![]() można wówczas określić na kilka sposobów - albo uogólniając w naturalny sposób
odpowiednie definicje albo np. jako całkę
można wówczas określić na kilka sposobów - albo uogólniając w naturalny sposób
odpowiednie definicje albo np. jako całkę ![]() .
.
Będziemy zakładać, że ![]() oraz
oraz ![]() jest filtracją spełniającą zwykłe
warunki taką, że
jest filtracją spełniającą zwykłe
warunki taką, że ![]() jest
jest ![]() -mierzalne oraz
-mierzalne oraz ![]() jest niezależne od
jest niezależne od
![]() dla
dla ![]() (za
(za ![]() można przyjąć uzupełnienie
można przyjąć uzupełnienie ![]() ).
).
8.1. Całka Paleya-Wienera
Definiowanie całki stochastycznej względem procesu Wienera zaczniemy od najprostszego przypadku funkcji deterministycznych.
Dla funkcji schodkowej postaci
![h=\sum _{{i=1}}^{k}\alpha _{i}{\mathrm{I}}_{{(t_{{i-1}},t_{i}]}},\quad 0=t_{0}<t_{1}<\ldots<t_{k}=t,\,\alpha _{i}\in{\mathbb{R}},](wyklady/was/mi/mi1062.png) |
określamy
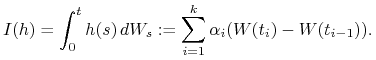 |
Z podstawowych własności procesu Wienera natychmiast otrzymujemy następujące
własności przekształcenia ![]() :
:
Stwierdzenie 8.1
Przy powyżej wprowadzonych oznaczeniach mamy
i) ![]() ,
,
ii) ![]() ,
,
iii) ![]() ma rozkład normalny
ma rozkład normalny ![]() ,
,
iii) ![]() dla
dla ![]() .
.
Oznaczając przez ![]() zbiór funkcji schodkowych na
zbiór funkcji schodkowych na ![]() widzimy, że przekształcenie
widzimy, że przekształcenie
![]() definiuje liniową izometrię
definiuje liniową izometrię ![]() . Ponieważ
funkcje schodkowe są gęste w
. Ponieważ
funkcje schodkowe są gęste w ![]() izometrię w jednoznaczny sposób możemy rozszerzyć na
całe
izometrię w jednoznaczny sposób możemy rozszerzyć na
całe ![]() .
.
Definicja 8.1
Rozszerzenie powyższej izometrii do izometrii na ![]() nazywamy całką Paleya-Wienera z
funkcji
nazywamy całką Paleya-Wienera z
funkcji ![]() i oznaczamy
i oznaczamy ![]() .
.
Stwierdzenie 8.2
Dla dowolnej funkcji ![]() ,
,
i) ![]() ,
,
ii) ![]() ,
,
iii) ![]() ma rozkład normalny
ma rozkład normalny ![]() .
.
Można też udowodnić następujące proste własności całki Paleya-Wienera:
Stwierdzenie 8.3
i) Jeżeli ![]() , to
, to
Ponadto dla dowolnego ![]() ,
,
ii) ![]()
oraz
iii) ![]() p.n. dla dowolnych
p.n. dla dowolnych ![]() .
.
8.2. Procesy elementarne
Starając się przenieść konstrukcję Paleya-Wienera na przypadek całki z procesów, musimy określić stochastyczny odpowiednik funkcji schodkowych - są to tak zwane procesy elementarne.
Definicja 8.2
Powiemy, że proces ![]() należy do
należy do
![]() - rodziny procesów elementarnych
(elementarnych procesów prognozowalnych), jeśli
- rodziny procesów elementarnych
(elementarnych procesów prognozowalnych), jeśli ![]() jest postaci
jest postaci
![X_{t}=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{k=1}}^{{m}}\xi _{{k-1}}{\mathrm{I}}_{{(t_{{k-1}},t_{k}]}}(t),](wyklady/was/mi/mi1122.png) |
(8.1) |
gdzie ![]() , zaś
, zaś ![]() są ograniczonymi zmiennymi losowymi,
są ograniczonymi zmiennymi losowymi,
![]() -mierzalnymi.
-mierzalnymi.
Oczywiście ![]() jest przestrzenią liniową.
jest przestrzenią liniową.
Definicja 8.3
Dla ![]() definiujemy proces
definiujemy proces
wzorem
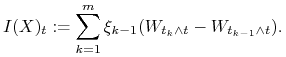 |
Uwaga 8.1
Definicja jest poprawna, tzn. nie zależy od reprezentacji ![]() .
.
Stwierdzenie 8.4
Jeśli ![]() jest procesem elementarnym, to proces
jest procesem elementarnym, to proces ![]() jest
martyngałem względem
jest
martyngałem względem ![]() ,
o ciągłych trajektoriach takim, że
,
o ciągłych trajektoriach takim, że ![]() oraz
oraz
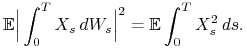 |
Przyjmijmy, że ![]() jest postaci (8.1).
Ciągłość trajektorii i
jest postaci (8.1).
Ciągłość trajektorii i ![]() wynika natychmiast z określenia
wynika natychmiast z określenia ![]() .
Jeżeli
.
Jeżeli ![]() , to zmienna
, to zmienna
jest ![]() mierzalna. Ponadto
mierzalna. Ponadto ![]() dla
dla ![]() .
.
Sprawdzimy teraz, że ![]() jest martyngałem, czyli dla
jest martyngałem, czyli dla ![]() mamy
mamy
![]() .
Wystarczy pokazać to dla
.
Wystarczy pokazać to dla ![]() , ale wtedy
, ale wtedy
wykorzystujemy tu założenie, że ![]() jest
jest ![]() mierzalne.
By zakończyć dowód liczymy
mierzalne.
By zakończyć dowód liczymy
![\displaystyle\sum _{{k=1}}^{{m}}{\mathbb{E}}[\xi _{{k-1}}^{2}(W_{{t_{k}}}-W_{{t_{{k-1}}}})^{2}]](wyklady/was/mi/mi946.png) |
||||
Wykorzystując mierzalność ![]() oraz niezależność przyrostów procesu Wienera mamy
oraz niezależność przyrostów procesu Wienera mamy
![I_{1}=\sum _{{k}}{\mathbb{E}}[\xi _{{k-1}}^{2}{\mathbb{E}}((W_{{t_{k}}}-W_{{t_{{k-1}}}})^{2}|{\mathcal{F}}_{{t_{{k-1}}}})]=\sum _{{k}}{\mathbb{E}}\xi _{{k-1}}^{2}(t_{k}-t_{{k-1}})={\mathbb{E}}\int _{{0}}^{{T}}X_{s}^{2}\, ds](wyklady/was/mi/mi1053.png) |
oraz
bo ![]()
Uwaga 8.2
Jedyne własności procesu Wienera jakie wykorzystywaliśmy w dowodzie, to
![]() oraz
oraz ![]() dla
dla ![]() .
Własności te można formalnie wyprowadzić z faktu, że procesy
.
Własności te można formalnie wyprowadzić z faktu, że procesy ![]() i
i
![]() są martyngałami względem
są martyngałami względem ![]() .
.
8.3. Martyngały ciągłe, całkowalne z kwadratem
Definicja 8.4
Przez ![]() oznaczamy przestrzeń martyngałów
oznaczamy przestrzeń martyngałów ![]() względem filtracji
względem filtracji ![]() o trajektoriach ciągłych takich, że
o trajektoriach ciągłych takich, że ![]() .
.
Uwaga 8.3
i) Jeśli ![]() , to z nierówności Jensena wynika, że
, to z nierówności Jensena wynika, że
![]() , więc
, więc ![]() jest podmartyngałem.
jest podmartyngałem.
ii) Przestrzeń ![]() można utożsamić z przestrzenią
martyngałów ciągłych
można utożsamić z przestrzenią
martyngałów ciągłych ![]() takich, że
takich, że ![]() .
Możemy bowiem określić
.
Możemy bowiem określić ![]() jako granicę p.n.
jako granicę p.n. ![]() przy
przy ![]() (zob. Twierdzenie 6.5 dla
(zob. Twierdzenie 6.5 dla ![]() ).
).
iii) Z nierówności Dooba (Twierdzenie 5.1) wynika, że dla
![]() ,
,
Twierdzenie 8.1
Przestrzeń ![]() jest przestrzenią Hilberta
(tzn. zupełną przestrzenią euklidesową)
z iloczynem skalarnym
jest przestrzenią Hilberta
(tzn. zupełną przestrzenią euklidesową)
z iloczynem skalarnym
oraz normą
Uwaga 8.4
i) Przy rozważaniach dotyczących całki stochastycznej utożsamiamy procesy nieodróżnialne.
Formalnie rzecz biorąc elementy ![]() to klasy abstrakcji martyngałów ciągłych
względem relacji nieodróżnialności.
to klasy abstrakcji martyngałów ciągłych
względem relacji nieodróżnialności.
ii) Przekształcenie ![]() jest izometrycznym włożeniem przestrzeni
jest izometrycznym włożeniem przestrzeni ![]() w
w
![]() .
.
Dowód Twierdzenia
Oczywiście ![]() jest przestrzenią liniową, zaś
jest przestrzenią liniową, zaś ![]() jest iloczynem skalarnym, bo
jest dwuliniowy, symetryczny,
jest iloczynem skalarnym, bo
jest dwuliniowy, symetryczny, ![]() oraz jeśli
oraz jeśli
![]() , to
, to ![]() , czyli
, czyli ![]() p.n., co z własności martygału implikuje, że
p.n., co z własności martygału implikuje, że
![]() p.n., więc z ciągłości
p.n., więc z ciągłości ![]() ,
, ![]() .
.
Musimy jeszcze udowodnić zupełność. Niech
![]() będzie ciągiem Cauchy'ego, czyli
będzie ciągiem Cauchy'ego, czyli
Wówczas ![]() jest ciągiem Cauchy'ego w
jest ciągiem Cauchy'ego w ![]() , zatem z zupełności
, zatem z zupełności
![]() istnieje całkowalna z kwadratem zmienna
istnieje całkowalna z kwadratem zmienna ![]() taka, że
taka, że
![]() przy
przy ![]() .
.
Możemy położyć ![]() , ale taka definicja nie gwarantuje ciągłości
, ale taka definicja nie gwarantuje ciągłości
![]() . Udowodnimy, że można znaleźć martyngał
. Udowodnimy, że można znaleźć martyngał ![]() , który jest ciągłą modyfikację
, który jest ciągłą modyfikację ![]() .
.
Zauważmy, że na mocy nierówności Dooba,
więc możemy wybrać podciąg ![]() taki, że
taki, że
Wówczas
Zatem, jeśli określimy
to ![]() , czyli na mocy lematu Borela-Cantelli,
, czyli na mocy lematu Borela-Cantelli,
![]() .
.
Jeśli ![]() , to
, to ![]() dla
dla ![]() , czyli
, czyli
![]() dla
dla ![]() . Ciąg
. Ciąg
![]() jest zatem zbieżny jednostajnie na
jest zatem zbieżny jednostajnie na ![]() do pewnej funkcji
do pewnej funkcji
![]() . Kładziemy dodatkowo
. Kładziemy dodatkowo ![]() dla
dla ![]() .
.
Z ciągłości ![]() wynika ciągłość
wynika ciągłość ![]() .
Ponieważ
.
Ponieważ ![]() w
w ![]() więc również w
więc również w ![]() , czyli
, czyli
![]() w
w ![]() , a że
, a że
![]() p.n., więc
p.n., więc
![]() p.n.,
czyli
p.n.,
czyli ![]() jest martyngałem ciągłym.
jest martyngałem ciągłym.
8.4. Całka izometryczna Itô. Procesy prognozowalne
Każdemu procesowi elementarnemu ![]() przyporządkowaliśmy martyngał ciągły
przyporządkowaliśmy martyngał ciągły ![]() , co więcej
przekształcenie
, co więcej
przekształcenie ![]()
jest liniową izometrią. Przekształcenie ![]() możemy więc rozszerzyć do liniowej izometrii
(którą też będziemy oznaczać literą
możemy więc rozszerzyć do liniowej izometrii
(którą też będziemy oznaczać literą ![]() )
z
)
z ![]() w
w ![]() , gdzie
, gdzie ![]() oznacza domknięcie
przestrzeni procesów elementarnych w
oznacza domknięcie
przestrzeni procesów elementarnych w
![]() .
.
Definicja 8.5
Tak zdefiniowane przekształcenie ![]() przyporządkowujące każdemu procesowi
przyporządkowujące każdemu procesowi
![]() z przestrzeni
z przestrzeni ![]() ciągły, całkowalny z
kwadratem martyngał
ciągły, całkowalny z
kwadratem martyngał ![]() nazywamy izometryczną całką stochastyczną Itô z procesu
nazywamy izometryczną całką stochastyczną Itô z procesu ![]() i
oznaczamy
i
oznaczamy
Oczywiście natychmiast powstaje pytanie jak wygląda przestrzeń ![]() , czyli
jakie procesy stochastyczne umiemy całkować.
, czyli
jakie procesy stochastyczne umiemy całkować.
Definicja 8.6
![]() -ciało zbiorów prognozowalnych
-ciało zbiorów prognozowalnych ![]() , to
, to ![]() -ciało podzbiorów
-ciało podzbiorów
![]() generowane przez
zbiory postaci
generowane przez
zbiory postaci ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Proces ![]() jest prognozowalny, jeśli traktowany jako funkcja
jest prognozowalny, jeśli traktowany jako funkcja
![]() jest mierzalny względem
jest mierzalny względem ![]() .
.
Z definicji natychmiast wynika, że ![]() jest prognozowalny,
jeśli
jest prognozowalny,
jeśli ![]() oraz
oraz ![]() .
.
Ponieważ każdą ograniczoną zmienną ![]() ,
, ![]() –mierzalną można aproksymować jednostajnie
przez zmienne postaci
–mierzalną można aproksymować jednostajnie
przez zmienne postaci ![]() ,
, ![]() , więc proces
, więc proces
![]() jest prognozowalny dla dowolnej ograniczonej zmiennej
jest prognozowalny dla dowolnej ograniczonej zmiennej ![]() ,
,
![]() –mierzalnej.
–mierzalnej.
Zatem dowolny proces ![]() jest prognozowalny, czyli
jest prognozowalny, czyli
![]() stąd
stąd
W szczególności każdy proces z ![]() jest nieodróznialny od
procesu prognozowalnego.
Okazuje się, że zachodzi również odwrotne
zawieranie.
jest nieodróznialny od
procesu prognozowalnego.
Okazuje się, że zachodzi również odwrotne
zawieranie.
Stwierdzenie 8.5
Mamy ![]() .
.
Wobec poprzednich rozważań musimy tylko pokazać, że
![]() Rozważymy dwa przypadki.
Rozważymy dwa przypadki.
Przypadek I: ![]() .
.
Najpierw pokażemy, że jeśli ![]() , to
, to
![]() .
W tym celu określmy
.
W tym celu określmy ![]() oraz
oraz
Łatwo sprawdzić, że ![]() jest
jest ![]() -układem, ponadto jeśli
-układem, ponadto jeśli
![]() , to
, to ![]() ,
a zatem
,
a zatem ![]() .
Co więcej
.
Co więcej ![]() jest
jest ![]() -układem dla
-układem dla ![]() , bo
, bo
i) ![]() , czyli
, czyli ![]() , gdyż
biorąc ciąg
, gdyż
biorąc ciąg ![]() , otrzymujemy
, otrzymujemy ![]() .
.
ii) ![]() ,
, ![]() ,
,
![]() z
liniowości
z
liniowości ![]() , czyli
, czyli ![]() .
.
iii) ![]() wstępujący, wówczas
wstępujący, wówczas
![]() ,
czyli
,
czyli ![]() .
.
Zatem dla ![]() , z twierdzenia o
, z twierdzenia o ![]() - i
- i ![]() -układach
-układach
![]()
Dalej, jeśli ![]() ,
, ![]() , to
, to
![]() (z liniowości).
Ponadto funkcje proste
(z liniowości).
Ponadto funkcje proste ![]() są gęste w
są gęste w
![]() , czyli
, czyli
![]()
Przypadek II: ![]() .
.
Niech ![]() oraz
oraz ![]() .
Wówczas procesy
.
Wówczas procesy
![]() są prognozowalne, należą do
są prognozowalne, należą do ![]() ,
zatem
,
zatem ![]() na mocy przypadku I.
na mocy przypadku I.
Ponadto ![]() w
w ![]() (tw. Lebesgue'a o zbieżności zmajoryzowanej), czyli
(tw. Lebesgue'a o zbieżności zmajoryzowanej), czyli ![]() .
.
Określiliśmy zatem ![]() dla procesów prognozowalnych całkowalnych
z kwadratem względem miary
dla procesów prognozowalnych całkowalnych
z kwadratem względem miary ![]() na
na ![]() .
Od tej pory przyjmujemy następujące oznaczenie
.
Od tej pory przyjmujemy następujące oznaczenie
 |
Dobrze by było jeszcze wiedzieć, że klasa procesów prognozowalnych jest dostatecznie duża, wynika to z następującego faktu:
Stwierdzenie 8.6
Jeśli ![]() jest procesem adaptowalnym i lewostronnie ciągłym, to
jest procesem adaptowalnym i lewostronnie ciągłym, to ![]() jest prognozowalny.
jest prognozowalny.
Dla ![]() określmy
określmy
![X_{t}^{{(n)}}:=X_{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{k=1}}^{{2^{n}-1}}X_{{\frac{k-1}{2^{n}}T}}{\mathrm{I}}_{{(\frac{k-1}{2^{n}}T,\frac{k}{2^{n}}T]}},](wyklady/was/mi/mi987.png) |
zaś w przypadku ![]() niech
niech
![X_{t}^{{(n)}}:=X_{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{k=1}}^{{n2^{n}}}X_{{\frac{k-1}{2^{n}}}}{\mathrm{I}}_{{(\frac{k-1}{2^{n}},\frac{k}{2^{n}}]}}.](wyklady/was/mi/mi990.png) |
Łatwo zauważyć, że procesy ![]() są prognozowalne oraz z lewostronnej ciągłości
są prognozowalne oraz z lewostronnej ciągłości ![]() wynika, że
wynika, że
![]() punktowo. Prognozowalność
punktowo. Prognozowalność ![]() wynika z faktu, że
granica punktowa ciągu funkcji mierzalnych jest mierzalna.
wynika z faktu, że
granica punktowa ciągu funkcji mierzalnych jest mierzalna.
Uwaga 8.5
Można udowodnić, że dla ![]() -adaptowalnego procesu
-adaptowalnego procesu ![]() takiego, że
takiego, że
![]() istnieje proces prognozowalny
istnieje proces prognozowalny ![]() taki, że
taki, że ![]() dla
dla ![]() prawie wszystkich
prawie wszystkich ![]() . Pozwala to określić
. Pozwala to określić
![]() dla procesów adaptowalnych z
dla procesów adaptowalnych z ![]() .
.
8.5. Zadania
Ćwiczenie 8.1
Oblicz ![]() dla
dla ![]() .
.
Ćwiczenie 8.2
Wykaż, że dla ![]() i
i ![]() zachodzi
zachodzi
Ćwiczenie 8.3
Wykaż, że dla ![]() zachodzi
zachodzi
Ćwiczenie 8.4
Niech ![]() .
Wykaż, że dla
.
Wykaż, że dla ![]() , przekształcenie
, przekształcenie
![]() jest izometrycznym włożeniem
jest izometrycznym włożeniem
![]() w
w ![]() .
.
Ćwiczenie 8.5
Wykaż, że proces
![Y_{{t}}=\left\{\begin{array}[]{ll}(1-t)\int _{{0}}^{{t}}\frac{1}{1-s}dW_{{s}}&0\leq t<1,\\
0&t=1\end{array}\right.](wyklady/was/mi/mi1128.png) |
ma takie same rozkłady skończenie wymiarowe co proces ![]() (most Browna).
(most Browna).
Ćwiczenie 8.6
Wykaż, że jeśli ![]() oraz
oraz
![]() jest ograniczoną zmienną losową
jest ograniczoną zmienną losową ![]() mierzalną to
mierzalną to
![]() oraz
oraz ![]() (Uwaga:
(Uwaga: ![]() definiujemy jako
definiujemy jako ![]() ).
).
Ćwiczenie 8.7
Wykaż, że jeśli ![]() oraz
oraz ![]() są zmiennymi
losowymi w
są zmiennymi
losowymi w ![]() ,
, ![]() mierzalnymi to proces
mierzalnymi to proces
![]() należy do
należy do ![]() oraz
oraz ![]() .
.
Ćwiczenie 8.8
Załóżmy, że ![]() jest procesem prognozowalnym, ciągłym w
jest procesem prognozowalnym, ciągłym w ![]() (tzn.
(tzn. ![]() jest ciągła z
jest ciągła z ![]() w
w ![]() ). Wykaż, że
wówczas
). Wykaż, że
wówczas ![]() oraz dla dowolnego ciągu podziałów
oraz dla dowolnego ciągu podziałów
![]() o
średnicy zbiegającej do zera zachodzi dla
o
średnicy zbiegającej do zera zachodzi dla ![]() ,
,
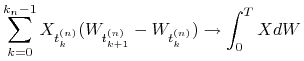 |
w ![]() przy
przy ![]() .
.
Ćwiczenie 8.9
Oblicz ![]() .
.




