Zagadnienia

9.1 Twierdzenie o zatrzymaniu całki stochastycznej
9.2 Uogólnienie definicji całki stochastycznej
9.3 Martyngały lokalne
9.4 Zadania

9. Własności całki izometrycznej. Uogólnienie definicji całki stochastycznej

Poprzednio zdefiniowaliśmy całkę $\int XdW$ dla $X\in{\mathcal{L}}^{2}_{T}$ . Czasami jednak potrzeba zdefiniować całkę względem procesu Wienera z procesu ciągłego $X$ dla którego $\int{\mathbb{E}}X_{t}^{2}dt=\infty$ . Podczas tego wykładu pokażemy jak określić taką całkę.

9.1. Twierdzenie o zatrzymaniu całki stochastycznej

Zacznijmy od prostej obserwacji.

Stwierdzenie 9.1

Jeśli $X\in{\mathcal{L}}_{T}^{2}$ , to dla dowolnego $u<T$ , ${\mathrm{I}}_{{[0,u]}}X\in{\mathcal{L}}_{T}^{2}$ i

$\int _{{0}}^{{t}}{\mathrm{I}}_{{[0,u]}}(s)X_{s}\, dW_{s}=\int _{{0}}^{{t\wedge u}}X_{s}\, dW_{s}\quad\mbox{ dla }0\leq t\leq T.$

Funkcja $(t,\omega)\rightarrow{\mathrm{I}}_{{[0,u]}}(t)$ jest deterministyczna, więc prognozowalna, zatem proces ${\mathrm{I}}_{{[0,u]}}X$ jest prognozowalny jako iloczyn procesów prognozowalnych, stąd ${\mathrm{I}}_{{[0,u]}}X\in{\mathcal{L}}_{T}^{2}$ .

Jeśli $X$ jest procesem elementarnym postaci $X=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{k}\xi _{k}{\mathrm{I}}_{{(t_{{k-1}},t_{k}]}}$ , to $X{\mathrm{I}}_{{[0,u]}}=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{k}\xi _{k}{\mathrm{I}}_{{(t_{{k-1}}\wedge u,t_{k}\wedge u]}}\in{\mathcal{E}}$ oraz

$\int _{{0}}^{{t}}{\mathrm{I}}_{{[0,u]}}(s)X_{s}\, dW_{s}=\sum\xi _{k}(W_{{t_{k}\wedge u\wedge t}}-W_{{t_{{k-1}}\wedge u\wedge t}})=\int _{{0}}^{{t\wedge u}}X_{s}\, dW_{s}.$

Dla $X\in{\mathcal{L}}_{T}^{2}$ weźmy $X^{{(n)}}\in{\mathcal{E}}$ takie, że $X^{{(n)}}\rightarrow X$ w ${\mathcal{L}}_{T}^{2}$ . Wówczas oczywiście również $X^{{(n)}}{\mathrm{I}}_{{[0,u]}}\rightarrow X{\mathrm{I}}_{{[0,u]}}$ w ${\mathcal{L}}_{T}^{2}$ . Stąd

$\int _{{0}}^{{t}}X_{s}{\mathrm{I}}_{{[0,u]}}(s)dW_{s}\leftarrow\int _{{0}}^{{t}}X_{s}^{{(n)}}{\mathrm{I}}_{{[0,u]}}(s)dW_{s}=\int _{{0}}^{{t\wedge u}}X_{s}^{{(n)}}dW_{s}\rightarrow\int _{{0}}^{{t\wedge u}}X_{s}dW_{s}.$

∎

Uogólnieniem faktu jest ważne twierdzenie o zatrzymaniu całki stochastycznej.

Twierdzenie 9.1

Niech $X\in{\mathcal{L}}_{T}^{2}$ oraz $\tau$ będzie momentem zatrzymania. Wówczas ${\mathrm{I}}_{{[0,\tau]}}X\in{\mathcal{L}}_{T}^{2}$ oraz

$\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}(s)X_{s}\, dW_{s}=\int _{{0}}^{{t\wedge\tau}}X_{s}\, dW_{s}\quad\mbox{ dla }0\leq t\leq T.$

(9.1)

Biorąc $\tau\wedge T$ zamiast $T$ możemy zakładać, że $\tau\leq T$ p.n..

Proces ${\mathrm{I}}_{{[0,\tau]}}(t)$ jest lewostronnie ciągły i adaptowalny, a zatem jest prognozowalny, czyli ${\mathrm{I}}_{{[0,\tau]}}X$ jest prognozowalny (iloczyn funkcji mierzalnych jest funkcją mierzalną). Stąd ${\mathrm{I}}_{{[0,\tau]}}X\in{\mathcal{L}}_{T}^{2}$ .

Wzór (9.1) udowodnimy w trzech krokach.

Krok 1. $X\in{\mathcal{E}}$ , $\tau$ przyjmuje skończenie wiele wartości.

Ewentualnie powiększając ciąg $t_{i}$ możemy zakładać, że $\tau$ przyjmuje wartości $0=t_{0}\leq t_{1}\leq\ldots\leq t_{m}\leq T$ oraz $X=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{k=0}}^{{m-1}}\xi _{k}{\mathrm{I}}_{{(t_{k},t_{{k+1}}]}}$ . Mamy

	$\displaystyle{\mathrm{I}}_{{[0,\tau]}}(t)$	$\displaystyle=\sum _{{k=0}}^{{m}}{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{[0,t_{k}]}}(t)=\sum _{{k=0}}^{m}\Big(\Big(\sum _{{j=0}}^{{k-1}}{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t)\Big)+{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{\{ 0\}}}\Big)$
		$\displaystyle={\mathrm{I}}_{{\Omega}}{\mathrm{I}}_{{\{ 0\}}}(t)+\sum _{{j=0}}^{{m-1}}\sum _{{k=j+1}}^{m}{\mathrm{I}}_{{\{\tau=t_{k}\}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t)$
		$\displaystyle={\mathrm{I}}_{{\Omega}}{\mathrm{I}}_{{\{ 0\}}}(t)+\sum _{{j=0}}^{{m-1}}{{\mathrm{I}}_{{\{\tau>t_{j}\}}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t),$

zatem

${\mathrm{I}}_{{[0,\tau]}}(t)X=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}(t)+\sum _{{j=0}}^{{m-1}}\xi _{j}{\mathrm{I}}_{{\{\tau>t_{j}\}}}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}(t),$

czyli ${\mathrm{I}}_{{[0,\tau]}}(t)X\in{\mathcal{E}}$ . Liczymy

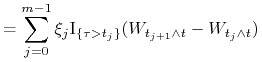	$\displaystyle\int _{{0}}^{{t}}{\mathrm{I}}_{{[0,\tau]}}(s)X_{s}\, dW_{s}$	$\displaystyle=\sum _{{j=0}}^{{m-1}}\xi _{j}{\mathrm{I}}_{{\{\tau>t_{j}\}}}(W_{{t_{{j+1}}\wedge t}}-W_{{t_{j}\wedge t}})$
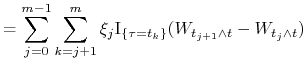		$\displaystyle=\sum _{{j=0}}^{{m-1}}\sum _{{k=j+1}}^{{m}}\xi _{j}{\mathrm{I}}_{{\{\tau=t_{k}\}}}(W_{{t_{{j+1}}\wedge t}}-W_{{t_{j}\wedge t}})$
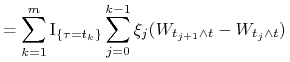		$\displaystyle=\sum _{{k=1}}^{{m}}{\mathrm{I}}_{{\{\tau=t_{k}\}}}\sum _{{j=0}}^{{k-1}}\xi _{j}(W_{{t_{{j+1}}\wedge t}}-W_{{t_{j}\wedge t}})$
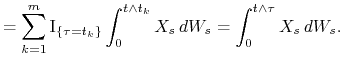		$\displaystyle=\sum _{{k=1}}^{{m}}{\mathrm{I}}_{{\{\tau=t_{k}\}}}\int _{0}^{{t\wedge t_{k}}}X_{s}\, dW_{s}=\int _{0}^{{t\wedge\tau}}X_{s}\, dW_{s}.$

Krok 2. $\tau$ dowolne oraz $X\in{\mathcal{E}}$ .

Weźmy ciąg momentów zatrzymania $\tau _{n}$ przyjmujących skończenie wiele wartości taki, że $\tau _{n}\searrow\tau$ . Na mocy kroku 1, para $(\tau _{n},X)$ spełnia (9.1). Z ciągłości trajektorii całki stochastycznej, $\int _{{0}}^{{t\wedge\tau _{n}}}X_{s}\, dW_{s}\rightarrow\int _{0}^{{t\wedge\tau}}X_{s}\, dW_{s}$ p.n.. Mamy

	$\displaystyle{\mathbb{E}}\Big(\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}(s)X_{s}\, dW_{s}-\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}(s)X_{s}\, dW_{s}\Big)^{2}$	$\displaystyle={\mathbb{E}}\Big(\int _{0}^{t}{\mathrm{I}}_{{(\tau,\tau _{n}]}}(s)X_{s}\, dW_{s}\Big)^{2}$
		$\displaystyle={\mathbb{E}}\int _{0}^{t}{\mathrm{I}}_{{(\tau,\tau _{n}]}}(s)X_{s}^{2}\, ds\rightarrow 0.$

Zbieżność wynika z twierdzenia Lebesgue'a, gdyż proces ${\mathrm{I}}_{{(\tau,\tau _{n}]}}(s)X_{s}^{2}$ dąży punktowo do zera i jest majoryzowany przez $X_{s}^{2}$ . Stąd

$\int _{0}^{{t\wedge\tau}}X\, dW\stackrel{p.n.}{\longleftarrow}\int _{0}^{{t\wedge\tau _{n}}}X\, dW=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\stackrel{L_{2}(\Omega)}{\longrightarrow}\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}X\, dW,$

czyli spełnione jest (9.1).

Krok 3. $\tau$ oraz $X\in{\mathcal{L}}_{T}^{2}$ dowolne.

Weźmy $X^{{(n)}}\in{\mathcal{E}}$ takie, że $X^{{(n)}}\rightarrow X$ w ${\mathcal{L}}_{T}^{2}$ . Z kroku 2, para $(\tau,\, X^{{(n)}})$ spełnia (9.1). Mamy

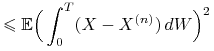	$\displaystyle{\mathbb{E}}\Big(\int _{{0}}^{{t\wedge\tau}}(X_{s}-X_{s}^{{(n)}})\, dW_{s}\Big)^{2}$	$\displaystyle\leq{\mathbb{E}}\Big(\int _{{0}}^{{T}}(X-X^{{(n)}})\, dW\Big)^{2}$
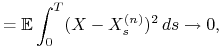		$\displaystyle={\mathbb{E}}\int _{{0}}^{{T}}(X-X^{{(n)}}_{s})^{2}\, ds\rightarrow 0,$

gdzie pierwsza nierówność wynika z nierówności Jensena oraz Twierdzenia Dooba 6.3 dla martyngału $(\int(X-X^{{(n)}})\, dW)$ . Ponadto

	$\displaystyle{\mathbb{E}}\Big(\int _{{0}}^{{t}}{\mathrm{I}}_{{[0,\tau]}}(s)(X_{s}-X_{s}^{{(n)}})\, dW_{s}\Big)^{2}$	$\displaystyle={\mathbb{E}}\int _{{0}}^{{t}}{\mathrm{I}}_{{[0,\tau]}}(s)(X_{s}-X_{s}^{{(n)}})^{2}\, ds$
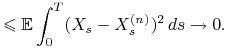		$\displaystyle\leq{\mathbb{E}}\int _{{0}}^{{T}}(X_{s}-X_{s}^{{(n)}})^{2}\, ds\rightarrow 0.$

Stąd

$\int _{0}^{{t\wedge\tau}}X_{s}\, dW_{s}\stackrel{L_{2}(\Omega)}{\longleftarrow}\int _{{0}}^{{t\wedge\tau}}X_{s}^{{(n)}}\, dW_{s}=\int _{{0}}^{{t}}{\mathrm{I}}_{{[0,\tau]}}X_{s}^{{(n)}}\, dW_{s}\stackrel{L_{2}(\Omega)}{\longrightarrow}\int _{0}^{{t}}{\mathrm{I}}_{{[0,\tau]}}X_{s}\, dW_{s},$

czyli (9.1) spełnione jest i w tym przypadku.

∎

Wniosek 9.1

Dla $X\in{\mathcal{L}}_{T}^{2}$ , proces $M:=((\int _{0}^{t}X\, dW)^{2}-\int _{0}^{t}X^{2}\, ds)_{{t\leq T}}$ jest martyngałem.

Dla $X\equiv 1$ otrzymujemy znany fakt, że $W_{t}^{2}-t$ jest martyngałem.

Dowód wniosku oparty jest na następującej prostej obserwacji.

Stwierdzenie 9.2

Załóżmy, że $M$ jest adaptowalnym, prawostronnie ciągłym procesem takim, że $M_{0}=0$ i dla wszystkich t, ${\mathbb{E}}|M_{t}|<\infty$ . Wówczas $M$ jest martyngałem wtedy i tylko wtedy gdy ${\mathbb{E}}M_{{\tau}}=0$ dla wszystkich ograniczonych momentów zatrzymania $\tau$ .

$\Rightarrow$ : Z Twierdzenia Dooba 6.3, ${\mathbb{E}}M_{{\tau}}={\mathbb{E}}M_{0}=0$ .

$\Leftarrow$ : Musimy pokazać, że dla $s<t$ , ${\mathbb{E}}(M_{t}|{\mathcal{F}}_{s})=M_{s}$ p.n., czyli ${\mathbb{E}}M_{t}{\mathrm{I}}_{A}={\mathbb{E}}M_{s}{\mathrm{I}}_{A}$ dla wszystkich $A\in{\mathcal{F}}_{s}$ . Określmy

$\tau:=\left\{\begin{array}[]{ll}s\mbox{ dla }\omega\in A,\\ t\mbox{ dla }\omega\not\in A.\end{array}\right.$

Jak łatwo sprawdzić $\tau$ jest momentem zatrzymania, stąd

$0={\mathbb{E}}M_{{\tau}}={\mathbb{E}}M_{s}{\mathrm{I}}_{A}+{\mathbb{E}}M_{t}{\mathrm{I}}_{{A^{c}}}={\mathbb{E}}M_{s}{\mathrm{I}}_{A}-{\mathbb{E}}M_{t}{\mathrm{I}}_{A},$

gdzie ostatnia równość wynika z faktu, że

${\mathbb{E}}M_{t}{\mathrm{I}}_{{A^{c}}}={\mathbb{E}}M_{t}-{\mathbb{E}}M_{t}{\mathrm{I}}_{A}=0-{\mathbb{E}}M_{t}{\mathrm{I}}_{A}.$

∎

Dowód Wniosku

Jak wiemy $\int X\, dW\in M_{T}^{{2,c}}$ , czyli proces $M$ jest ciągły, adaptowalny i całkowalny oraz $M_{0}=0$ . Dla ograniczonego momentu zatrzymania $\tau\leq T$ otrzymujemy na mocy twierdzenia o zatrzymaniu całki stochastycznej

${\mathbb{E}}\Big(\int _{{0}}^{{\tau}}X\, dW\Big)^{2}={\mathbb{E}}\Big(\int _{{0}}^{{T}}{\mathrm{I}}_{{[0,\tau]}}X\, dW\Big)^{2}={\mathbb{E}}\int _{{0}}^{{T}}{\mathrm{I}}_{{[0,\tau]}}(s)X_{s}^{2}\, ds={\mathbb{E}}\int _{{0}}^{{\tau}}X_{s}^{2}\, ds.$

Zatem

${\mathbb{E}}M_{{\tau}}={\mathbb{E}}\Big[\Big(\int _{{0}}^{{\tau}}X\, dW\Big)^{2}-\int _{{0}}^{{\tau}}X_{s}^{2}\, ds\Big]=0.$

Teza Wniosku wynika ze Stwierdzenia 9.2.

∎

9.2. Uogólnienie definicji całki stochastycznej

Definicja 9.1

Dla $T\leq\infty$ określamy przestrzeń procesów prognozowalnych, lokalnie całkowalnych z kwadratem

$\Lambda^{2}_{T}=\Big\{(X_{t})_{{t<T}}-\mbox{ prognozowalny}\colon\ \int _{0}^{t}X_{s}^{2}\, ds<\infty\mbox{ p.n. dla }0<t<T\Big\}.$

Zatem proces prognozowalny $X$ należy do przestrzeni $\Lambda^{2}_{T}$ wtedy i tylko wtedy, gdy

${\mathbb{P}}\Big(\forall _{{t<T}}\,\,\int _{0}^{t}X_{s}^{2}\, ds<\infty\Big)=1.$

Przestrzeń $\Lambda^{2}_{T}$ jest liniowa, ale nie jest przestrzenią Hilberta.

Lemat 9.1

Dla $X\in\Lambda^{2}_{T}$ określmy

$\tau _{n}:=\inf\Big\{ t\geq 0:\,\int _{0}^{t}X_{s}^{2}\, ds\geq n\Big\}\wedge T\wedge n,\,\, n=1,2,\ldots.$

Wówczas $(\tau _{n})$ jest rosnącym ciagiem momentów zatrzymania, $\tau _{n}\nearrow T$ p.n. Ponadto dla wszystkich $n$ , ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ .

$\tau _{n}$ jest momentem zatrzymania gdyż jest definiowany poprzez moment dojścia przez adaptowalny proces ciągły $\int _{0}^{t}X_{s}^{2}\, ds$ do zbioru domkniętego $[n,\infty)$ . Z założenia o skończoności $\int X_{s}^{2}\, ds$ wynika, że $\tau _{n}\nearrow T$ p.n..

Proces ${\mathrm{I}}_{{[0,\tau _{n}]}}X$ jest prognozowalny jako iloczyn procesów prognozowalnych, ponadto na mocy nierówności Schwarza i definicji $\tau _{n}$ ,

${\mathbb{E}}\Big(\int _{0}^{T}{\mathrm{I}}_{{[0,\tau _{n}]}}(s)X_{s}\, ds\Big)^{2}={\mathbb{E}}\Big(\int _{0}^{{\tau _{n}}}X_{s}\, ds\Big)^{2}\leq{\mathbb{E}}\Big[\tau _{n}\int _{0}^{{\tau _{n}}}X_{s}^{2}\, ds\Big]\leq n^{2}<\infty.$

∎

Załóżmy, że mamy dany rosnący ciąg momentów zatrzymania $\tau _{n}\nearrow T$ p.n. taki, że ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ dla wszystkich $n$ . Niech $M_{n}(t):=\int _{{0}}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X_{s}\, dW_{s}$ . Przypomnijmy też, że przez $X^{{\tau}}$ oznaczamy proces $X$ zatrzymany w chwili $\tau$ (zob. Definicja 4.9).

Lemat 9.2

Dla $m\geq n$ , procesy $M_{m}^{{\tau _{n}}}$ i $M_{n}$ są nierozróżnialne, czyli

${\mathbb{P}}(\forall _{{t\leq T}}\ M_{m}(t\wedge\tau _{n})=M_{n}(t))=1.$

Na mocy twierdzenia o zatrzymaniu całki stochastycznej dla ustalonego $t\leq T$ ,

	$\displaystyle M_{m}(\tau _{n}\wedge t)$	$\displaystyle=\int _{0}^{{\tau _{n}\wedge t}}{\mathrm{I}}_{{[0,\tau _{m}]}}X\, dW=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}{\mathrm{I}}_{{[0,\tau _{m}]}}X\, dW$
		$\displaystyle=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW=M_{n}(t).$

Zatem $M_{m}^{{\tau}}$ jest modyfikacją $M_{n}$ . Teza lematu wynika z ciągłości obu procesów.

∎

Definicja 9.2

Niech $X\in\Lambda^{2}_{T}$ oraz $\tau _{n}$ będzie rosnącym do $T$ ciągiem momentów zatrzymania takich, że ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ dla wszystkich $n$ . Całką stochastyczną $\int X\, dW$ dla $X\in\Lambda^{2}_{T}$ nazywamy taki proces $(M_{t})_{{t<T}}=(\int _{0}^{t}X\, dW)_{{t<T}}$ , że $M^{{\tau _{n}}}_{t}=\int _{0}^{{t\wedge\tau _{n}}}X\, dW=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW$ dla $n=1,2,\ldots$ .

Stwierdzenie 9.3

Proces $M$ zdefiniowany powyżej jest jest ciągły i jednoznacznie określony w klasie procesów nieodróżnialnych.

Na mocy Lematu 9.2 dla każdego $m>n$ istnieje zbiór $N_{{n,m}}$ taki, że ${\mathbb{P}}(N_{{n,m}})=0$ oraz dla $\omega\not\in N_{{n,m}}$ zachodzi $M_{n}(t,\omega)=M_{m}(t\wedge\tau _{{n}}(\omega),\omega)$ dla wszystkich $t<T$ . Niech $N:=\bigcup _{{m>n}}N_{{n,m}}$ , wówczas ${\mathbb{P}}(N)=0$ oraz dla $\omega\notin N$ , $t\leq\tau _{{n}}(\omega)$ ciąg $(M_{{m}}(t,\omega))_{{m\geq n}}$ jest stały. Zatem możemy (i musimy) położyć $M(t,\omega):=M_{n}(t,\omega)$ dla $t\leq\tau _{n}(\omega)$ .

∎

Stwierdzenie 9.4

Definicja $\int X\, dW$ nie zależy od wyboru ciągu $\tau _{n}$ dla $X\in\Lambda _{T}^{2}$ . Dokładniej, jeśli $\tau _{n}$ , $\overline{\tau}_{n}$ - momenty zatrzymania, $\tau _{n}\nearrow T$ , $\overline{\tau}_{n}\nearrow T$ , ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ i ${\mathrm{I}}_{{[0,\overline{\tau}_{n}]}}X\in{\mathcal{L}}_{T}^{2}$ oraz $M,\overline{M}$ określone jak w Definicji 9.2 za pomocą $\tau _{n}$ , $\overline{\tau}_{n}$ odpowiednio, to procesy $M$ i $\overline{M}$ są nierozróżnialne.

Mamy

$M_{{t\wedge\tau _{n}}}=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW,\quad\overline{M}_{{t\wedge\overline{\tau}_{n}}}=\int _{0}^{t}{\mathrm{I}}_{{[0,\overline{\tau}_{n}]}}X\, dW.$

Na mocy twierdzenia o zatrzymaniu całki stochastycznej,

$M_{{t\wedge\tau _{n}\wedge\overline{\tau}_{n}}}=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}{\mathrm{I}}_{{[0,\overline{\tau}_{n}]}}X\, dW=\overline{M}_{{t\wedge\tau _{n}\wedge\overline{\tau}_{n}}}.$

Ponadto $\tau _{n}\wedge\overline{\tau}_{n}\nearrow T$ , więc ${t\wedge\tau _{n}\wedge\overline{\tau}_{n}}=t$ dla $n\geq n(\omega)$ i stąd $M_{t}=\overline{M}_{t}$ p.n., a że są to procesy ciągłe, to są nierozróżnialne.

∎

Sformułujemy teraz uogólnienie twierdzenia o zatrzymaniu całki stochastycznej.

Twierdzenie 9.2

Jeśli $X\in\Lambda^{2}_{T}$ , to dla dowolnego momentu zatrzymania $\tau$ , ${\mathrm{I}}_{{[0,\tau]}}X\in\Lambda^{2}_{T}$ oraz

$\int _{0}^{{t\wedge\tau}}X\, dW=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}X\, dW.$

Proces ${\mathrm{I}}_{{[0,\tau]}}X$ jest prognozowalny jako iloczyn procesów prognozowalnych, jest majoryzowany przez $X$ , stąd ${\mathrm{I}}_{{[0,\tau]}}X\in\Lambda^{2}_{T}$ . Proces $X\in\Lambda^{2}_{T}$ , więc istnieje ciąg $\tau _{n}\nearrow T$ taki, że ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ . Wtedy też ${\mathrm{I}}_{{[0,\tau _{n}]}}{\mathrm{I}}_{{[0,\tau]}}X\in{\mathcal{L}}_{T}^{2}$ . Niech

$M:=\int X\, dW,\quad N:=\int{\mathrm{I}}_{{[0,\tau]}}X\, dW.$

Na mocy definicji,

$M_{{t\wedge\tau _{n}}}=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X,dW,\quad N_{{t\wedge\tau _{n}}}=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}{\mathrm{I}}_{{[0,\tau]}}X\, dW.$

Z udowodnionego wcześniej Twierdzenia 9.1 o zatrzymaniu całki izometrycznej,

$M_{{t\wedge\tau\wedge\tau _{n}}}=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW=N_{{t\wedge\tau _{n}}}.$

Biorąc $n\rightarrow\infty$ dostajemy $M^{{\tau}}_{{t}}=M_{{t\wedge\tau}}=N_{{t}}$ , czyli $M^{{\tau}}=N$ .

∎

9.3. Martyngały lokalne

Definicja 9.3

Jeżeli dla procesu adaptowalnego $M=(M_{{t}})_{{t<T}}$ , istnieje ciąg momentów zatrzymania $\tau _{n}\nearrow T$ taki, że $M^{{\tau _{n}}}$ jest martyngałem, to $M$ nazywamy martyngałem lokalnym. Jeśli dodatkowo $M^{{\tau _{n}}}\in{\mathcal{M}}_{T}^{{2,c}}$ , to mówimy, że $M$ jest ciągłym martyngałem lokalnym całkowalnym z kwadratem. Klasę takich procesów oznaczamy ${\mathcal{M}}_{{T,{\rm loc}}}^{{2,c}}$ ( ${\mathcal{M}}_{{{\rm loc}}}^{{2,c}}$ jeśli wartość $T$ jest jasna z kontekstu).

Uwaga 9.1

$M-M_{0}\in{\mathcal{M}}^{{c}}_{{T,{\rm loc}}}$ wtedy i tylko wtedy, gdy $M-M_{0}\in{\mathcal{M}}^{{2,c}}_{{T,{\rm loc}}}$ , gdzie ${\mathcal{M}}^{{c}}_{{T,{\rm loc}}}$ oznacza rodzinę ciągłych martyngałów lokalnych.

Stwierdzenie 9.5

Załóżmy, że $M=\int XdW$ dla $X\in\Lambda _{{2}}^{T}$ . Wówczas
i) $M$ jest procesem ciągłym, $M_{0}=0$ ,
ii) $M\in{\mathcal{M}}_{{T,{\rm loc}}}^{{2,c}}$ ,
iii) Przekształcenie $X\rightarrow\int XdW$ jest liniowe.

Punkty i), ii) wynikają z definicji. By udowodnić iii) weźmy $X,Y\in\Lambda _{T}^{2}$ . Istnieją wówczas momenty zatrzymania $\tau _{n}\nearrow T$ i $\overline{\tau}_{n}\nearrow T$ takie, że ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ oraz ${\mathrm{I}}_{{[0,\overline{\tau}_{n}]}}Y\in{\mathcal{L}}_{T}^{2}$ . Przyjmując $\sigma _{n}:=\overline{\tau}_{n}\wedge\tau _{n}\nearrow T$ otrzymujemy ${\mathrm{I}}_{{[0,\sigma _{n}]}}X,\,{\mathrm{I}}_{{[0,\sigma _{n}]}}Y\in{\mathcal{L}}_{T}^{2}$ , a zatem ${\mathrm{I}}_{{[0,\sigma _{n}]}}(aX+bY)\in{\mathcal{L}}_{T}^{2}$ dla dowolnych $a,b\in{\mathbb{R}}$ . Stąd na mocy definicji otrzymujemy, że $\int _{0}^{{t\wedge\sigma _{n}}}(aX+bY)\, dW=a\int _{0}^{{t\wedge\sigma _{n}}}X\, dW+b\int _{0}^{{t\wedge\sigma _{n}}}Y\, dW$ i biorąc granicę $n\rightarrow\infty$ , $\int(aX+bY)\, dW=a\int XdW+b\int YdW.$

∎

Uwaga 9.2

Martyngał lokalny $M=\int X\, dW$ dla $X\in\Lambda _{T}^{2}$ nie musi być martyngałem, $M_{t}$ nie musi być nawet całkowalne. Ale, jeśli ${\mathbb{E}}\int _{0}^{t}X_{s}^{2}\, ds<\infty$ dla wszystkich $t<T$ , to $M$ jest martyngałem, bo możemy przyjąć $\tau _{n}=t_{n}$ , gdzie $t_{n}$ jest ciągiem rosnącym zbieżnym do $T$ i wtedy $M_{{t\wedge\tau _{n}}}=M_{{t\wedge t_{n}}}\in{\mathcal{M}}_{T}^{{2,c}}$ .

Uwaga 9.3

Przykłady ciągłych martyngałów lokalnych, które nie są martyngałami są podane w Ćwiczeniach 13.4 i 13.6.

Mimo, że w przypadku ogólnym $\int X\, dW$ nie musi być martyngałem, to zachodzi dla tego procesu nierówność Dooba.

Twierdzenie 9.3 (Nierówność Dooba)

Dla dowolnego procesu $X\in\Lambda _{{2}}^{T}$ oraz momentu zatrzymania $\tau\leq T$ ,

${\mathbb{E}}\sup _{{t<\tau}}\Big(\int _{0}^{t}X\, dW\Big)^{2}\leq 4{\mathbb{E}}\int _{0}^{{\tau}}X_{s}^{2}\, ds.$

Weźmy $\tau _{n}\nearrow T$ takie, że ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}$ . Mamy

	$\displaystyle{\mathbb{E}}\sup _{{t<\tau}}$	$\displaystyle\Big(\int _{0}^{{t\wedge\tau _{n}}}X\, dW\Big)^{2}={\mathbb{E}}\sup _{{t<\tau}}\Big(\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}$
		$\displaystyle={\mathbb{E}}\sup _{{t<T}}\Big(\int _{0}^{{t\wedge\tau}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}={\mathbb{E}}\sup _{{t\leq T}}\Big(\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2},$

${\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{M}}^{{2,c}}_{T}$ , więc $t<T$ można zamienić na $t\leq T$ . Na mocy nierówności Dooba dla martyngałów,

	$\displaystyle{\mathbb{E}}\sup _{{t\leq T}}\Big(\int _{0}^{t}{\mathrm{I}}_{{[0,T]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}$	$\displaystyle\leq 4{\mathbb{E}}\Big(\int _{0}^{T}{\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dW\Big)^{2}$
		$\displaystyle=4{\mathbb{E}}\int _{0}^{T}({\mathrm{I}}_{{[0,\tau]}}{\mathrm{I}}_{{[0,\tau _{n}]}}X_{s})^{2}\, ds=4{\mathbb{E}}\int _{0}^{{\tau\wedge\tau _{n}}}X_{s}^{2}\, ds$
		$\displaystyle\leq 4{\mathbb{E}}\int _{0}^{{\tau}}X_{s}^{2}\, ds.$

Wykazaliśmy zatem, że

${\mathbb{E}}\sup _{{t<\tau}}\Big(\int _{0}^{{t\wedge\tau _{n}}}X\, dW\Big)^{2}\leq 4{\mathbb{E}}\int _{0}^{{\tau}}X_{s}^{2}\, ds.$

Ponieważ

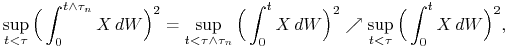$\sup _{{t<\tau}}\Big(\int _{0}^{{t\wedge\tau _{n}}}X\, dW\Big)^{2}=\sup _{{t<\tau\wedge\tau _{n}}}\Big(\int _{0}^{{t}}X\, dW\Big)^{2}\nearrow\sup _{{t<\tau}}\Big(\int _{0}^{{t}}X\, dW\Big)^{2},$

więc teza wynika z twierdzenia Lebesgue'a o zbieżności monotonicznej.

∎

Stwierdzenie 9.6

a) Każdy ograniczony martyngał lokalny jest martyngałem.
b) Każdy nieujemny martyngał lokalny jest nadmartyngałem.

Załóżmy, że $\tau _{n}\nearrow T$ jest ciągiem momentów zatrzymania takim, że dla każdego $n$ , $M^{{\tau _{n}}}$ jest martyngałem. Ustalmy $s<t<T$ oraz $A\in{\mathcal{F}}_{s}$ .

a) Jeśli $M$ jest ograniczony, to z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej,

${\mathbb{E}}M_{t}{\mathrm{I}}_{A}\leftarrow{\mathbb{E}}M_{{\tau _{n}\wedge t}}{\mathrm{I}}_{A}={\mathbb{E}}M^{{\tau _{n}}}_{t}{\mathrm{I}}_{A}={\mathbb{E}}M^{{\tau _{n}}}_{s}{\mathrm{I}}_{A}={\mathbb{E}}M_{{\tau _{n}\wedge s}}{\mathrm{I}}_{A}\rightarrow{\mathbb{E}}M_{s}{\mathrm{I}}_{A},$

stąd $M$ jest martyngałem.

b) Jeśli $M$ jest nieujemny, to

	$\displaystyle{\mathbb{E}}M_{s}{\mathrm{I}}_{A}$	$\displaystyle=\lim _{{n\rightarrow\infty}}{\mathbb{E}}M_{s}{\mathrm{I}}_{{A\cap\{\tau _{n}>s\}}}=\lim _{{n\rightarrow\infty}}{\mathbb{E}}M_{{s}}^{{\tau _{n}}}{\mathrm{I}}_{{A\cap\{\tau _{n}>s\}}}=\lim _{{n\rightarrow\infty}}{\mathbb{E}}M_{{t}}^{{\tau _{n}}}{\mathrm{I}}_{{A\cap\{\tau _{n}>s\}}}$
		$\displaystyle\geq{\mathbb{E}}\lim _{{n\rightarrow\infty}}M_{{t}}^{{\tau _{n}}}{\mathrm{I}}_{{A\cap\{\tau _{n}>s\}}}={\mathbb{E}}M_{t}{\mathrm{I}}_{A},$

gdzie korzystaliśmy z twierdzenia Lebesgue'a o zbieżności monotonicznej, tego, że $M^{{\tau _{n}}}$ jest martyngałem i $A\cap\{\tau _{n}>s\}\in{\mathcal{F}}_{s}$ oraz z lematu Fatou.

∎

9.4. Zadania

Ćwiczenie 9.1

Niech $\tau$ będzie momentem zatrzymania takim, że ${\mathbb{E}}\tau<\infty$ . Wykaż, że ${\mathrm{I}}_{{[0,\tau]}}\in{\cal L}^{{2}}_{{\infty}}$ oraz $\int _{{0}}^{{\infty}}{\mathrm{I}}_{{[0,\tau]}}(s)dW_{{s}}=W_{{\tau}}$ . Wywnioskuj stąd, że ${\mathbb{E}}W_{{\tau}}=0$ oraz ${\mathbb{E}}W_{{\tau}}^{{2}}={\mathbb{E}}\tau$ .

Ćwiczenie 9.2

Dla $a,b>0$ określmy $\tau:=\inf\{ t:|W_{{t}}|=a\sqrt{b+t}\}$ . Wykaż, że $\tau<\infty$ p.n. oraz ${\mathbb{E}}\tau<\infty$ wtedy i tylko wtedy gdy $a<1$ . Ponadto dla $a<1$ , ${\mathbb{E}}\tau=\frac{a^{{2}}b}{1-a^{{2}}}$ .

Ćwiczenie 9.3

Wykaż, że dla $X\in\Lambda^{{2}}_{{T}}$ , $(\int X\, dW)^{2}-\int X^{2}\, ds$ jest ciągłym martyngałem lokalnym.

Ćwiczenie 9.4

Niech $X\in\Lambda^{{2}}_{{T}}$ , $0\leq t<s\leq T$ oraz $\xi$ będzie zmienną losową ${\mathcal{F}}_{{t}}$ -mierzalną (niekoniecznie ograniczoną). Wykaż, że $\xi X{\mathrm{I}}_{{(t,s]}}\in\Lambda^{{2}}_{{T}}$ oraz $\int _{{t}}^{{s}}\xi XdW=\xi\int _{{t}}^{{s}}XdW$ .