10. Dedukcyjne bazy danych
10.1. Bazy danych z perspektywy logiki
Spojrzenie na bazy danych oczami logika pozwala jednolicie opisać szereg używanych pojęć. Do opisu relacyjnych baz danych używa się zwykle rachunku predykatów bez symboli funkcyjnych.
Fakty zapisane w wierszach tabel reprezentuje się literałami, np. Ojciec(Jan,Piotr)
gdzie pierwszy symbol (Ojciec) odpowiada nazwie tabeli, a pozostałe zawartości pewnego wiersza w tej tabeli.
Taki sposób opisu obejmuje również najprostsze realizacje baz danych, np. gdy fakty przechowuje się w postaci pojedynczej listy, wczytywanej do pamięci z pliku podczas ładowania bazy danych i zapisywanej na pliku przy zamykaniu bazy.
Tak więc reprezentacją relacji Zwierzaki:
| gatunek | imię | waga |
| Papuga | Kropka | 3,50 |
| Papuga | Lulu | 5,35 |
| Papuga | Hipek | 3,50 |
| Lis | Fufu | 6,35 |
| Krokodyl | Czako | 75,00 |
będą następujące literały
| Zwierzak(Papuga,Kropka,3.50) |
| Zwierzak(Papuga,Lulu,5.35) |
| Zwierzak(Papuga,Hipek,3.50) |
| Zwierzak(Lis,Fufu,6.35) |
| Zwierzak(Krokodyl,Czako,75.00) |
(dla nazwy relacji w rachunku predykatów użyjemy liczby pojedynczej, bo jest naturalniejsza).
10.1.1. (CWA:Closed World Assumption)
W relacyjnych bazach danych obowiązuje założenie o zamkniętości świata.
Definicja 10.1 (Założenie o zamkniętości świata)
Przyjmuje się, że jeśli fakt nie znajduje się w odpowiedniej tabeli w bazie danych, to nie zachodzi (jest fałszywy). Inaczej mówiąc, jeśli wiersz
nie znajduje się w relacji ![]() , to zachodzi
, to zachodzi
Mówiąc potocznie, jeśli czegoś nie wiem, to powinienem przyjąć, że nie jest to prawdziwe. W przeciwnym razie odpowiedzi na zapytanie SELECT w SQL musiałyby się kończyć frazą ,,… i być może jeszcze coś, o czym nie wiem”.
Dla bazy danych z podaną przed chwilą relacją Zwierzaki będzie więc spełnione (na przykład):
|
|
i wiele innych zanegowanych literałów.
10.1.2. Domain closure assumption
Założenie o zamkniętości dziedziny (a właściwie dziedzin) mówi, że nie istnieją inne ,,obiekty” niż występujące w tabelach bazy danych.
Definicja 10.2 (Założenie o zamkniętości dziedziny)
Nie ma innych indywiduów niż te znajdujące się w bazie danych. Inaczej mówiąc, nie ma innych stałych niż te, które występują w wierszach bazy danych.
Założenie to spełniają systemy ograniczające niejawnie swoją dziedzinę ,,referencji”. Przykład: algebra relacji (bo wszelkie wyrażenia powstają przez składanie relacji początkowych).
W relacyjnych bazach danych używających SQL założenia tego nie spełniają oczywiście liczby całkowite i rzeczywiste. Zwykle natomiast spełniają je napisy, np. nie ima innych nazw zwierzaków niż te podane w tabeli Zwierz.
Unique name assumption
Definicja 10.3 (Założenie o unikalności nazw)
Indywidua (stałe) o różnych nazwach są różne. Inaczej mówiąc, nie ma aksjomatów równościowych dla stałych.
Unikalność nazw: przykład
-
W naszej przykładowej bazie
Zwierzak(Papuga,Kropka,3.50) Zwierzak(Papuga,Lulu,5.35) Zwierzak(Papuga,Hipek,3.50) Zwierzak(Lis,Fufu,6.35) Zwierzak(Krokodyl,Czako,75.00) -
zachodzi
Zwierzak(Krokodyl,Fufu,6.35)
-
ponieważ zakładamy, że zachodzi
Krokodyl
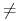 Lis
Lis
Zapytania
-
Do zapisywania zapytań będziemy używać formuł zawierających zmienne.
-
Ograniczymy się do formuł prostych.
-
Zapytania mają wtedy postać wzorców — struktur podobnych do faktów, mogących jednak zawierać zmienne.
-
Zmiennymi będą symbole poprzedzone znakami zapytania, np. Ojciec(Jan,?x)
jest zapytaniem o wszystkie dzieci Jana.
-
Odpowiedź na zapytanie składa się z bezpośrednio wyszukanych faktów pasujących do zapytania oraz z faktów wyprowadzonych przy użyciu reguł.
Klauzule
Definicja 10.4 (Klauzula)
Klauzulą nazywać będziemy formułę postaci
lub też równoważnie
Wyrażenia ![]() nazywać będziemy poprzednikami (lub
przesłankami, zaś wyrażenia
nazywać będziemy poprzednikami (lub
przesłankami, zaś wyrażenia ![]() następnikami lub
wnioskami klauzuli.
następnikami lub
wnioskami klauzuli.
Rodzaje klauzul
-
Klauzule bez poprzedników, zawierające tylko jeden następnik bez zmiennych
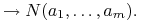
służą do reprezentowania faktów.
-
Klauzule bez następników

reprezentują negację poprzedników i mogą służyć do zapisywania ograniczeń (więzów poprawności). Stan bazy danych jest legalny, jeśłi nie jest spełniona koniunkcja poprzedników, np. Ojciec(?x,?y)
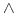 Matka(?x,?y)
Matka(?x,?y)  .
. -
Taka klauzula mająca tylko jeden poprzednik bez zmiennych zapisuje jawnie negację faktu, np. Ojciec(Jan,Piotr)
 .
.oznacza, że Jan nie jest ojcem Piotra.
-
Klauzula o pojedynczym następniku

służy w dedukcyjnych bazach danych do definiowania relacji R.
-
Jak zobaczymy dalej, pełna definicja relacji może wymagać kilku klauzul.
-
W relacyjnych bazach danych klauzule takie (tak jak i następne) służą do zapisywania ograniczeń.
-
Klauzule postaci
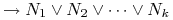
wyrażają wiedzę niekompletną: wiemy, że spełniony jest jeden lub więcej następników, ale nie wiemy który.
-
Przykład:
 Student(Jan,Matematyka)
Student(Jan,Matematyka) 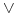 Student(Jan,Biologia)
Student(Jan,Biologia)
-
Klauzulą o pełnej postaci
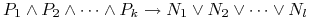
można interpretować jako warunkowe informacje o niekompletnej wiedzy.
-
Można też ich używać jako ograniczeń, np. aby zapisać, że każdy ma co najwyżej dwoje rodziców użyjemy
Rodzic(?p,?a)
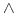 Rodzic(?q,?a)
Rodzic(?q,?a) 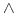 Rodzic(?r,?a)
Rodzic(?r,?a)
 (?p = ?q)
(?p = ?q) 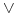 (?p = ?r)
(?p = ?r) 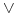 (?q = ?r)
(?q = ?r)
-
Klauzula pusta, czyli klauzula bez poprzedników i następników, oznacza fałsz.
-
Klauzula taka nie powinna nigdy wystąpić w niesprzecznej bazie danych.
10.2. Dedukcyjne bazy danych
W dedukcyjnych bazach danych dopuszcza się tylko niektóre rodzaje klauzul z programowania w logice.
-
Nakłada sie dodatkowe ograniczenia.
-
Brak symboli funkcyjnych.
-
Tylko jeden następnik.
-
Takie dedukcyjne bazy danych określa się jako definite.
-
-
Zmienna z konkluzji reguły musi wystąpić w jej treści.
-
Zapewnia to spełnienie założenia o zamkniętości dziedziny.
-
-
Jako predykaty obliczalne dozwolona tylko arytmetyka.
-
Zauważmy, że formalnie narusza to założenie o zamkniętości dziedziny.
-
-
-
Jednym z takich rozszerzeń relacyjnych baz danych jest Datalog.
Datalog
-
W Datalogu klauzule zapisujemy jako reguły.
-
Każdy predykat jest
-
albo ekstensjonalny: zdefiniowany wyłącznie przez fakty zapisane w bazie danych,
-
albo intensjonalny: zdefiniowany wyłącznie przez reguły.
-
-
Reguły mają nieco zmienioną postać zapisu następnik <- poprzednik AND ...
przy czym zarówno następnik jak i poprzedniki mają postać wzorców, na przykład P(?x,?y,?z) <- Q(?x,?y,?z) AND x > 10
-
Ponieważ takie reguły, podobnie jak klauzule, odpowiadają implikacjom z logiki, posiadają one zarówno interpretację logiczną jak i proceduralną.
-
Na przykład regule
Dziadek(?x,?z) <- Ojciec(?x,?y) AND Ojciec(?y,?z)
odpowiada implikacja
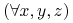 Ojciec(
Ojciec(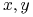 )
) 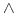 Ojciec(
Ojciec(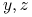 )
)  Dziadek(
Dziadek(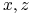 )
) -
Jeśli reguła nie zawiera poprzedników, to jej następnik jest zawsze spełniony.
-
Podobnie jak fakty, reguły przechowuje się także w bazie danych.
Reguły a zapytania
-
Reguła pasuje do zapytania, jeśli jej konkluzja pasuje do zapytania.
-
Znajdowanie odpowiedzi na zapytanie przy użyciu reguł polega na znalezieniu reguł pasujących do zapytania i dla każdej z nich wyszukanie w sposób spójny (tzn. tak, żeby wartości zmiennych były zgodne) odpowiedzi na podzapytania powstałe z przesłanek (czyli rekursja :-) i złożenie otrzymanych wyników, podstawiając otrzymane wartości zmiennych na zmienne w konkluzji.
-
Ostateczną odpowiedzią na zapytanie jest lista wyszukanych faktów (dla reguł będą to konkretyzacje ich konkluzji).
Zalety
-
Pozwalają otrzymywać odpowiedzi wymagające domknięcia przechodniego.
-
Przykład:
-
Mamy tabelę Zawiera(obiekt,składnik,ile) dotyczącą pojazdów (np. rowerów, sanek itp.) podającą obiekty i ich bezpośrednie składowe.
-
Chcemy otrzymać informację o wszystkich częściach wchodzących w skład obiektu 'rower'.
-
Przykładowa tabela
Zawiera
| obiekt | składnik | ile |
|---|---|---|
| rower | koło | 2 |
| koło | piasta | 1 |
| koło | obręcz | 1 |
| obręcz | szprycha | 20 |
| koło | opona | 1 |
| rower | rama | 1 |
| rama | siodełko | 1 |
| rama | kierownica | 1 |
Definicja predykatu Części
-
Definicja w Datalogu
Czesci(?calosc,?czesc) <- Zawiera(?calosc,?czesc,?_). Czesci(?calosc,?czesc) <- Zawiera(?calosc,?skladnik,?_) AND Czesci(?skladnik,?czesc). -
i samo zapytanie
Czesci('rower',?co) ?
Realizacja zapytań
-
W odróżnieniu od programowania w logice w Datalogu nie używa się nawracania.
-
Budowa odpowiedzi odbywa się bottom-up: rozpoczynamy od pustej relacji Czesci i iteracyjnie dodajemy do niej wszystkie wiersze, które w tym momencie można otrzymać z reguł.
-
Optymalizacja: w kążdym kroku używam reguł tylko dla wierszy dodanych w poprzednim kroku.
-
Zauważmy, że jest to typowy algorytm wyznaczania minimalnego punktu stałego (tzw. minimalnego modelu).
-
Z otrzymanej ekstensji relacji wybieramy tylko wiersze pasujące do zapytania.
Przykład obliczania odpowiedzi
-
Rozpoczynam od pustej tabeli Czesci.
-
Krok 1: z pierwszej reguły dodaję do niej wiersze <'rower','koło'>, <'koło','piasta'>, <'koło','obręcz'>, <'obręcz','szprycha'>, <'koło','opona'>, <'rower','rama'>, <'rama','siodełko'>, <'rama','kierownica'>.
-
Krok 2: używając drugiej reguły dodaję wiersze <'rower','piasta'>, <'rower','obręcz'>, <'rower','opona'>, <'rower','siodełko'>, <'rower','kierownica'>, <'koło','szprycha'>.
-
Krok 3: używając drugiej reguły dodaję wiersz <'rower','szprycha'>.
-
Krok 4: ponieważ żadna reguła nie produkuje już nowych wierszy, kończę iterację i wybieram wiersze <'rower','koło'>, <'rower','rama'>, <'rower','piasta'>, <'rower','obręcz'>, <'rower','opona'>, <'rower','siodełko'>, <'rower','kierownica'>, <'rower','szprycha'>.
Rekursja w SQL
-
Zapytania rekurencyjne w SQL-3 definiuje się konstrukcją
WITH [RECURSIVE] R(...) AS zapytanie używające R SELECT ...; -
Można tak zdefiniować kilka pomocniczych relacji wzajemnie rekurancyjnych.
Przykład rekursji w SQL
-
Zapiszemy nasze zapytanie z Datalogu w SQL
WITH RECURSIVE Czesci(calosc,czesc) AS (SELECT obiekt,skladnik FROM Zawiera) UNION (SELECT obiekt,czesc FROM Zawiera, Czesci WHERE skladnik = calosc) SELECT czesc FROM Czesci WHERE calosc = 'rower';
Negacja
-
W poprzednikach reguł Datalogu można poprzedzać predykaty negacją NOT.
-
Taki literał jest spełniony, jeśli ta negacja jest prawdziwa dla tego predykatu w minimalnym modelu.
-
Aby można to było sprawdzać, program z negacjami musi być stratyfikowalny: reguły predykatów intensjonalnych dzielimy na warstwy tak, by
-
Definicja predykatu nie była w wyższej warstwie, niż jego wykorzystanie w definicjach innych predykatów.
-
Negacja predykatu występowała w wyższej warstwie niż jego definicja.
-
-
Minimalne punkty stałe wyznaczamy kolejno poczynając od najniższej warstwy.
-
Podobne ograniczenie na poprawność rekursji z negacją obowiązuje w SQL-3.




