Zagadnienia
2. Algebra relacji
Algebra relacji jest modelem teoretycznym do opisywania semantyki relacyjnych baz danych, zaproponowanym przez T. Codda, twórcę koncepcji relacyjnych baz danych. Jest to algebra, w której dziedzinę stanowią relacje. Zmienne występujące w wyrażeniach tej algebry odpowiadają pojedynczym relacjom.
Operatory algebry relacji zostały dobrane tak, aby odpowiadały typowym operacjom występującym w zapytaniach podczas wyszukiwania informacji z tabel w bazie danych.
Tak określona algebra miała być językiem zapytań (query language) dla relacyjnych baz danych.
2.1. Relacje
Relacje w algebrze relacji reprezentujemy ich nazwami. Z nazwą każdej relacji jest związany jej schemat — ciąg nazw atrybutów (odpowiadających kolumnom modelowanej tabeli), np.
-
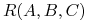
-
Student(indeks,imię,nazwisko)
Nazwy atrybutów w schemacie relacji muszą być różne, dlatego w literaturze schemat jest czasem definiowany jako zbiór nazw atrybutów, a nie ciąg.
Ponieważ relacje miały być abstrakcyjnym modelem tabel, ich elementy nazywa się często krotkami — odpowiadają one wierszom tabel z bazy danych.
2.2. Operacje
Zestaw operacji jest spory. Obejmuje po pierwsze typowe operacje
teoriomnogościowe: sumę zbiorów (![]() ), iloczyn zbiorów (
), iloczyn zbiorów (![]() ) i różnicę
zbiorów (
) i różnicę
zbiorów (![]() ). Wymaga się, aby oba argumenty miały ten sam schemat
atrybutów. Jeśli nazwy atrybutów różnią się, to należy użyć operacji
przemianowania (o czym za chwilę).
). Wymaga się, aby oba argumenty miały ten sam schemat
atrybutów. Jeśli nazwy atrybutów różnią się, to należy użyć operacji
przemianowania (o czym za chwilę).
Iloczyn kartezjański (![]() ) także jest zdefiniowany klasycznie.
Ponieważ jednak argumenty mogą mieć atrybuty o tych samych nazwach,
nazwy kolumn w schemacie wynikowym trzeba czasem poprzedzać nazwami
relacji, z których pochodzą, np. dla relacji
) także jest zdefiniowany klasycznie.
Ponieważ jednak argumenty mogą mieć atrybuty o tych samych nazwach,
nazwy kolumn w schemacie wynikowym trzeba czasem poprzedzać nazwami
relacji, z których pochodzą, np. dla relacji ![]() i
i ![]() schematem ich iloczynu kartezjańskiego będzie
schematem ich iloczynu kartezjańskiego będzie ![]() ,
tak jak w poniższym przykładzie
,
tak jak w poniższym przykładzie
R2 =
R1 =
A
B
1
2
3
4
B
C
5
6
7
8
9
10
R1
![]() R2 =
R2 =A
R1.B
R2.B
C
1
2
5
6
1
2
7
8
1
2
9
10
3
4
5
6
3
4
7
8
3
4
9
10
Lepiej jednak w takiej sytuacji użyć przemianowania.
2.2.1. Selekcja
Oprócz operacji teoriomnogościowych w algebrze relacji określono kilka
operacji (a właściwie rodzin operacji) specyficznych dla niej. Pierwsza
z nich to selekcja (wybór) ![]() . Zgodnie z nazwą
wybiera ona z relacji tylko te krotki, dla których jest spełniony podany
warunek.
. Zgodnie z nazwą
wybiera ona z relacji tylko te krotki, dla których jest spełniony podany
warunek.
Przypuśćmy, że w mamy relację Zwierzaki o następującej postaci:
| gatunek | imię | waga |
| Papuga | Kropka | 3,50 |
| Papuga | Lulu | 5,35 |
| Papuga | Hipek | 3,50 |
| Lis | Fufu | 6,35 |
| Krokodyl | Czako | 75,00 |
Wartością wyrażenia ![]() jest:
jest:
| gatunek | imię | waga |
| Papuga | Kropka | 3,50 |
| Papuga | Lulu | 5,35 |
| Papuga | Hipek | 3,50 |
2.2.2. Rzutowanie
Podobna do selekcji jest operacja rzutowania (projekcji)
![]() : z relacji wybieramy tylko podane kolumny.
Zwróćmy uwagę, że mogłoby to prowadzić do utworzenia relacji, w której
niektóre wiersze byłyby takie same. Ponieważ jednak relacje są zbiorami,
więc takie duplikaty są automatycznie eliminowane, tak jak w poniższym
przykładzie dla wyrażenia
: z relacji wybieramy tylko podane kolumny.
Zwróćmy uwagę, że mogłoby to prowadzić do utworzenia relacji, w której
niektóre wiersze byłyby takie same. Ponieważ jednak relacje są zbiorami,
więc takie duplikaty są automatycznie eliminowane, tak jak w poniższym
przykładzie dla wyrażenia ![]() :
:
| gatunek | waga |
|---|---|
| Papuga | 3,50 |
| Papuga | 5,35 |
| Lis | 6,35 |
| Krokodyl | 75,00 |
Ze względów praktycznych warto zdefiniować uogólnione rzutowanie,
w którym oprócz nazw kolumn dozwolone są dowolne wyrażenia oparte na
kolumnach, np. arytmetyczne. Trzeba je tylko wtedy nazwać:
![]()
Ponadto dopuszcza się, aby pewne kolumny wystąpiły wielokrotnie, wymagane jest jednak przemianowanie jak powyżej.
A oto przykład: dane jest relacja R
R =
A
B
1
2
3
4
Wartością wyrażenia ![]() R będzie
R będzie
C
A
A1
3
1
1
7
3
3
Wspominaliśmy wcześniej o operacji przemianowania ![]() :
nie powoduje ona żadnych zmian w zawartości relacji, lecz służy jedynie
:
nie powoduje ona żadnych zmian w zawartości relacji, lecz służy jedynie
-
do zmiany nazwy relacji:
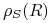
-
lub zmiany nazw jej atrybutów
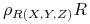 ,
, -
a czasem jednego i drugiego:
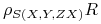 .
.
Złączenie ![]() : podobne
do iloczynu kartezjańskiego, ale łączy się ze sobą tylko pary
wierszy spełniające podany warunek
: podobne
do iloczynu kartezjańskiego, ale łączy się ze sobą tylko pary
wierszy spełniające podany warunek
-
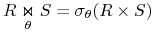
-
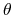 oznacza dowolny warunek na kolumny łączonych relacji,
np.
oznacza dowolny warunek na kolumny łączonych relacji,
np.  .
. -
Złączenie theta, w którym warunek jest prostą równością pary atrybutów, nazywa się złączeniem równościowym.
-
Pojęcie porzuconej krotki (dangling tuple): wiersza z jednej z relacji, do którego nie pasuje żaden wiersz z drugiej relacji.
-
Zwierzaki gatunek imię waga Papuga Kropka 3,50 Papuga Lulu 5,35 Papuga Hipek 3,50 Lis Fufu 6,35 Krokodyl Czako 75,00 Gatunki nazwa kontynent Papuga Ameryka Lis Europa Krokodyl Afryka -
Zwierzaki
 Gatunki
Gatunki
gatunek imię waga nazwa kontynent Papuga Kropka 3,50 Papuga Ameryka Papuga Lulu 5,35 Papuga Ameryka Papuga Hipek 3,50 Papuga Ameryka Lis Fufu 6,35 Lis Europa Krokodyl Czako 75,00 Krokodyl Afryka
-
Notacja:
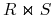 .
. -
Łączone relacje muszą mieć co najmniej jedną wspólną kolumnę o tej samej nazwie.
-
Warunkiem złączenia jest równość dla wszystkich par atrybutów o tych samych nazwach.
-
W wyniku zostaje tylko jedna kolumna z pary kolumn o tych samych nazwach.
-
Zwierzaki gatunek imię waga Papuga Kropka 3,50 Papuga Lulu 5,35 Papuga Hipek 3,50 Lis Fufu 6,35 Krokodyl Czako 75,00 Gatunki gatunek kontynent Papuga Ameryka Lis Europa Krokodyl Afryka -
Zwierzaki
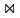 Gatunki
Gatunki
gatunek imię waga kontynent Papuga Kropka 3,50 Ameryka Papuga Lulu 5,35 Ameryka Papuga Hipek 3,50 Ameryka Lis Fufu 6,35 Europa Krokodyl Czako 75,00 Afryka
-
Pozwala na nazywanie relacji wynikowych:
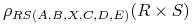 .
. -
Uproszczone notacja:
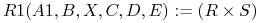 .
.
2.3. Wyrażenia
-
Ponieważ jest to algebra, więc operacje można składać otrzymując wyrażenia złożone.
-
Równoważność wyrażeń można wykorzystać przy optymalizacji, zastępując dane wyrażenie równoważnym mu, lecz bardziej efektywnym.
-
Zwierzaki gatunek imię waga Papuga Kropka 3,50 Papuga Lulu 5,35 Papuga Hipek 3,50 Lis Fufu 6,35 Krokodyl Czako 75,00 -
Znajdź pary zwierzaków (imiona) tego samego gatunku
![\pi _{{Z1.imie,Z2.imie}}(\rho _{{Z1}}Zwierzaki\underset{\begin{array}[]{l}\scriptstyle Z1.gatunek=Z2.gatunek\land\\
\scriptstyle Z1.imie<Z2.imie\end{array}}{\Join}\rho _{{Z2}}Zwierzaki)](wyklady/bad/mi/mi19.png)
-
Zgodnie z matematyczną definicją relacji jako zbioru utożsamia się jednakowe krotki (powstające np. podczas rzutowania).
-
Można rozszerzyć tę algebrę na wielozbiory, dopuszczając powtórzenia.
-
Powstaje jednak problem odpowiedniej semantyki dla operacji iloczynu i różnicy teoriomnogościowej.
-
Intuicyjnie zdefiniowane rozszerzenia operacji na wielozbiory zastosowane do relacji dają relacje z wyjątkiem sumy, która dla dwóch relacji może dać wielozbiór.
-
Przestają zachodzić niektóre prawa algebry relacji, np.
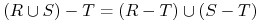
-
Operator eliminacji powtórzeń
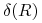 .
.
-
Operator grupowania z ewentualną agregacją
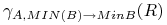
-
Zauważmy, że
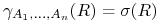
jeśli
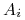 to wszystkie atrybuty
to wszystkie atrybuty 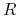 .
.
-
Operator sortowania
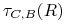 .
. -
Nie jest to operator algebry relacji ani wielozbiorów, lecz ewentualnej algebry list, dlatego powinien być zewnętrznym operatorem wyrażenia!
-
naturalne:
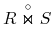
-
jako wypełniaczy brakujących wartości w dołączonych kolumnach używa się
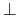 ;
;
-
-
lewostronne:
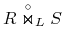
-
brane są tylko porzucone krotki z pierwszego argumentu;
-
-
prawostronne:
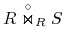 ;
; -
wersje theta powyższych (z warunkiem u dołu).
-
Zwierzaki gatunek imię waga Papuga Kropka 3,50 Papuga Lulu 5,35 Papuga Hipek 3,50 Lis Fufu 6,35 Krokodyl Czako 75,00 Gatunki gatunek kontynent Papuga Ameryka Lis Europa Krokodyl Afryka Krowa Europa -
Zwierzaki
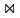 Gatunki
Gatunki
gatunek imię waga kontynent Papuga Kropka 3,50 Ameryka Papuga Lulu 5,35 Ameryka Papuga Hipek 3,50 Ameryka Lis Fufu 6,35 Europa Krokodyl Czako 75,00 Afryka Krowa 
Europa
2.4. Zastosowania algebry relacji
-
Zapisywanie zapytań (np. modelowanie semantyki)
-
Nakładanie ograniczeń na poprawność bazy danych (więzy). Przykłady:
![\begin{array}[]{ll}R\cap S=\emptyset&\mbox{(styl równościowy)}\\
R\cap S\subseteq\emptyset&\mbox{(styl teoriomnogościowy)}\end{array}](wyklady/bad/mi/mi42.png)
-
Integralność referencyjna
![\begin{array}[]{l}\pi _{{\mbox{\footnotesize\textit{klucz-zewnętrzny}}}}(R)\subseteq\pi _{{klucz}}(S)\\
\pi _{{\mbox{\footnotesize\textit{klucz-zewnętrzny}}}}(R)-\pi _{{klucz}}(S)=\emptyset\end{array}](wyklady/bad/mi/mi50.png)
-
Zależności funkcyjne
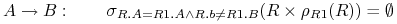
2.5. Zadania
Ćwiczenie 2.1
Dane są dowolne relacje ![]() ,
, ![]() ,
, ![]() algebry relacji oraz
wyrażenia (zapytania)
algebry relacji oraz
wyrażenia (zapytania)
|
|
|
|---|---|
|
|
Które z poniższych stwierdzeń są prawdziwe
-
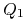 i
i 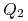 dają ten sam wynik
dają ten sam wynik -
Odpowiedź na
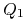 może mieć mniej elementów niż odpowiedź na
może mieć mniej elementów niż odpowiedź na 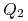
-
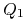 i
i 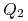 mogą dać inne wyniki.
mogą dać inne wyniki.
Pierwsze.
Ćwiczenie 2.2
Dane są relacje ![]() i
i ![]() , każda zawierająca
, każda zawierająca ![]() krotek.
Relacja
krotek.
Relacja ![]() ma
ma
-
co najmniej
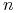 krotek
krotek -
co najwyżej
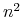 krotek
krotek -
zawsze
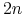 krotek
krotek
-
nie
-
tak
-
nie




