Zagadnienia
6. Teoria projektowania relacyjnych baz danych
6.1. Zależności funkcyjne
Zależność funkcyjna występuje wtedy, gdy po ustaleniu wartości pewnych atrybutów relacji wartości jakichś innych atrybutów tej relacji są jednoznacznie wyznaczone (unikalne).
Używa się notacji: ![]() , gdzie
, gdzie ![]() i
i ![]() są zbiorami atrybutów z relacji R.
są zbiorami atrybutów z relacji R.
Mówimy, że zależność funkcyjną ![]() zachodzi w R, jeśli każde dwa wiersze mające te same wartości
atrybutów z
zachodzi w R, jeśli każde dwa wiersze mające te same wartości
atrybutów z ![]() muszą mieć te same wartości atrybutów z
muszą mieć te same wartości atrybutów z ![]() .
.
Formalnie mozna to wyrazić następująco
choć funkcja ![]() nie jest oczywiście znana (albo czasem nie jest łatwa do
obliczenia).
nie jest oczywiście znana (albo czasem nie jest łatwa do
obliczenia).
6.1.1. Rozbicie zależności
Zależność funkcyjną, której prawa strona zawiera kilka atrybutów
można zastąpić zbiorem zależności o pojedynczych prawych stronach
Operacja ta jest oczywiście odwracalna.
Przykład: ![]() można zastąpić przez
można zastąpić przez ![]() i
i
![]() .
.
Uwaga:Nie wolno rozbijać lewych stron zależności!
6.1.2. Przykłady zależności
Jeśli w przykładowym ZOO każdy zwierzak nazywa się inaczej, to dla relacji
Zwierz(imie,gatunek,waga,wiek) zachodzi zależność:
imie ![]() gatunek
gatunek
Jeśli przyjęto (raczej naturalną) zasadę ,,Żadne dwa wykłady nie
odbywają się o tej samej godzinie w tej samej sali”, to mamy zależność
funkcyjną
godzina sala ![]() wykład
wykład
Jak określa się zależności dla danej relacji? Jedynie przez odpytanie użytkowników.
Nie należy natomiast liczyć na to, że wykryjemy je na podstawie zawartości tabeli w bazie danych. W takiej tabeli może być pozornie spełniona pewna zależność, która przestanie zachodzić za pięć minut (po dodaniu do tabeli nowych wierszy)! W ten sposób można jedynie upewnić się, że podana zależność nie zachodzi.
6.1.3. Zależności trywialne
Definicja 6.1
Zależność ![]() nazywamy trywialną, jeśli
spełnione jest
nazywamy trywialną, jeśli
spełnione jest ![]() .
.
Uwaga 6.1
Zależności trywialne zachodzą zawsze i nie dostarczają żadnej informacji.
6.2. Klucze
Jednym z ważniejszych pojęć w projektowaniu relacyjnych baz danych jest pojęcie klucza relacji. Zaczniemy od pomocniczej definicji.
Definicja 6.2
Podzbiór ![]() zbioru atrybutów relacji
zbioru atrybutów relacji ![]() nazywamy
jej nadkluczem, jeśli zachodzi zależność funkcyjna
nazywamy
jej nadkluczem, jeśli zachodzi zależność funkcyjna
Czyli zbiór wszystkich atrybutów relacji na pewno jest jej nadkluczem.
Definicja 6.3
Podzbiór ![]() zbioru atrybutów relacji
zbioru atrybutów relacji ![]() nazywamy
jej kluczem, jeśli jest on nadkluczem i żaden jego podzbiór
nie jest nadkluczem.
nazywamy
jej kluczem, jeśli jest on nadkluczem i żaden jego podzbiór
nie jest nadkluczem.
Inaczej mówiąc, klucze relacji to jej minimalne nadklucze. Obejrzymuy teraz przykłady kluczy.
Niech w relacji Zwierz zachodzi zależność
imie ![]() gatunek wiek waga
gatunek wiek waga
-
{imie,gatunek} jest nadkluczem w relacji Zwierz
-
Nie jest jednak kluczem, bo {imie} też jest nadkluczem
-
{imie} jest kluczem i nie ma innych kluczy
6.2.1. Skąd się biorą klucze?
Skąd się biorą klucze? Na ogół są wyznaczane z zależności funkcyjnych.
Czasem jednak otrzymane w ten sposób klucze obejmują zbyt wiele kolumn,
co jest w praktyce niewygodne. Wprowadza się wtedy arbitralnie tzw.
klucze sztuczne), dodając do relacji R nowy atrybut ![]() jako klucz.
Oznacza to nałożenie dodatkowej zależności funkcyjnej
jako klucz.
Oznacza to nałożenie dodatkowej zależności funkcyjnej
gdzie ![]() są atrybutami relacji R
są atrybutami relacji R
6.2.2. Wyprowadzanie zależności
Pewne zależności można wyprowadzić z innych. Przykład: jeśli zachodzi
i zachodzi
to musi zachodzić
Można to sprawdzić z definicji. Inny sposób to skorzystać z reguł wnioskowania Armstronga.
6.2.3. Domknięcie zbioru atrybutów
Definicja 6.4
Domknięciem zbioru atrybutów![]() (względem danego zbioru zależności)
nazywamy taki zbiór atrybutów
(względem danego zbioru zależności)
nazywamy taki zbiór atrybutów ![]() , że
, że
-
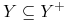
-
Dla dowolnej zależności
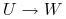 , jeśli
, jeśli 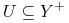 ,
to
,
to 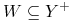
Jeśli ![]() , to zachodzi zależność funkcyjna
, to zachodzi zależność funkcyjna
![]() . Klucz jest to więc taki minimalny zbiór atrybutów,
że jego domknięcie jest zbiorem wszystkich atrybutów relacji.
. Klucz jest to więc taki minimalny zbiór atrybutów,
że jego domknięcie jest zbiorem wszystkich atrybutów relacji.
Dla przykładu policzymy domknięcie atrybutu ![]() z naszego przykładu
z naszego przykładu
-
Krok bazowy:
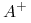 :=
:= 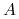
-
Indukcja: ponieważ
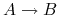 i
i 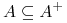 , to
, to
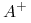 :=
:=  =
= 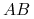
-
Indukcja: ponieważ
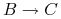 i
i 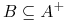 , to
, to
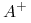 :=
:= 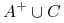 =
= 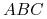
Wniosek: ponieważ ![]() , więc zachodzi
, więc zachodzi ![]() .
.
Spróbujmy innego przykładu. Dla zbioru zależności
domknięciem ![]() jest
jest ![]() , ponieważ
, ponieważ
6.2.4. Domknięcie zbioru zależności
Definicja 6.5
Domknięcie zbioru zależności![]() (oznaczane
(oznaczane ![]() ) jest to zbiór
wszystkich zależności, które można wyprowadzić z
) jest to zbiór
wszystkich zależności, które można wyprowadzić z ![]() .
.
Definicja 6.6 (Równoważność zbiorów zależności)
Dwa zbiory zależności ![]() i
i ![]() są równoważne, jeśli ich
domkniecia są równe:
są równoważne, jeśli ich
domkniecia są równe: ![]() wtw
wtw ![]() .
.
Definicja 6.7 (Minimalny zbiór zależności)
Minimalny zbiór zależności jest to taki zbiór zależności, który nie jest równoważny żadnemu swojemu podzbiorowi.
-
Uwaga: to jest uproszczona definicja, pełna jest bardziej skomplikowana.
-
Minimalny zbiór zależności dla danego wyjściowego zbioru zależności nie jest wyznaczony jednoznacznie.
6.2.5. Reguły wnioskowania Armstronga
Reguły wnioskowania Armstronga służą do wyprowadzania zależności z innych zależności.
![\begin{array}[]{lrl}\mbox{Zwrotność}&Y\subseteq X&\vdash X\rightarrow Y\\
\\
\mbox{Rozszerzanie}&X\rightarrow Y&\vdash XZ\rightarrow YZ\\
\\
\mbox{Przechodniość}&X\rightarrow Y,Y\rightarrow Z&\vdash X\rightarrow Z\end{array}](wyklady/bad/mi/mi136.png) |
6.3. Projektowanie schematu
6.3.1. Redundancja
Jeden z celów, który staramy się osiągnąć podczas projektowania schematu bazy danych to unikanie redundancji (nadmiarowości). Redundancja oznacza, że niektóre informacje są zapisane w bazie danych wielokrotnie. Prowadzi to do anomalii podczas modyfikacji i usuwania
-
Anomalia modyfikacji: informacja zostaje uaktualniona tylko w niektórych miejscach
-
Przykład: zmiana adresu studenta na nowy, jeśli informacja o studencie i jego adresie trzymana jest w kilku miejscach.
-
-
Anomalia usuwania: wraz z usunięciem ostatniego wiersza szczegółowego znika informacja ogólna
-
Gdyby informacje o adresie studenta trzymać przy przedmiotach, na które jest zarejestrowany, to po zakończeniu sesji (a przed nową rejestracją) adres ten by zniknął.
-
6.3.2. Przykład złego projektu
Obejrzyjmy przykład złego projektu i jego konsekwencje. Przypuśćmy, że mamy relację Zwierzaki(gatunek,imie,waga,kontynent) z następującymi zależnościami
| imie |
| gatunek |
Przykładowa zawartość takiej relacji
| gatunek | imie | waga | kontynent |
| Papuga | Kropka | 3,50 | ??? |
| Papuga | Lulu | 5,35 | Ameryka |
| Papuga | Hipek | 3,50 | ??? |
| Lis | Fufu | 6,35 | Europa |
| Krokodyl | Czako | 75,00 | Afryka |
Występuje redundancja, ponieważ wartości dla ??? można łatwo odgadnąć (czy jak kto woli wyznaczyć) na podstawie zależności.
6.4. Normalizacja
Normalizacja to proces, służący do przekształcenia schematu zawierającego redundancję w schemat, który jej nie zawiera. Zależnie od potrzeb określa się różne poziomy normalizacji — zakresy usuwania redundancji, nazywane postaciami normalnymi.
6.4.1. Postacie normalne
Dotychczas formalnie zdefiniowano pięć (poziomów) postaci normalnych, choć tylko trzy pierwsze są powszechnie używane podczas projektowania baz danych.
Postacie normalne są ponumerowane kolejno, ale istnieje postać pośrednia BCNF między 3 i 4 poziomem. Postacie o wyższych numerach automatycznie (z definicji) spełniają warunki dla niższych postaci, dlatego relacja w drugiej postaci normalnej jest automatycznie w pierwszej postaci normalnej.
Odwrotne wynikanie oczywiście nie zachodzi; drugą postać normalną otrzymujemy z pierwszej po nałożeniu dodatkowego warunku.
Proces normalizacji polega na dekompozycji tabel aż do otrzymania pożądanej postaci.
6.4.2. Pierwsza postać normalna (1NF)
Warunkiem pierwszej postaci normalnej jest to, by każdy atrybut w relacji przyjmował tylko wartości niepodzielne. Przez wartości niepodzielne rozumiemy takie pojedyncze wartości, jak używane w atrybutach ,,numer klienta” czy ,,nazwisko klienta”.
Relacja w pierwszej postaci normalnej nie może zawierać atrybutu, w którym można upakować kilka wartości, np. odddzielając je przecinkami.
Daty można traktować jako wartości niepodzielne lub tworzyć oddzielne atrybuty dla dnia, miesiąca i roku.
6.4.3. Druga postać normalna (2NF)
Aby stwierdzić, czy relacja będąca w pierwszej postaci normalnej jest także w drugiej, należy określić klucze relacji.
Każdej wartości klucza powinien jednoznacznie odpowiadać pojedynczy wiersz w tabeli. Na przykład dla relacji Zamówienie_klienta kluczem może być numer_zamówienia.
Warunkiem na drugą postać normalną jest to, aby każdy niekluczowy atrybut zależał funkcyjnie od całego klucza. Niedozwolone są więc tzw. zależności częściowe.
Uwaga: przypominamy, że kluczy może być kilka!
6.4.4. Trzecia postać normalna (3NF)
Dla sprawdzenia, czy relacja będąca w drugiej postaci normalnej jest także w trzeciej, bada się zależności między atrybutami niekluczowymi.
Atrybuty niekluczowe powinny zależeć funkcyjnie wyłącznie od klucza i niczego więcej. Wykluczamy w ten sposób zależności przechodnie.
6.4.5. Postać normalna Boyce-Codda (BCNF)
Bardziej restrykcyjna niż trzecia postać normalna jest postać normalna Boyce-Codda, lecz jest ona rzadziej wykorzystywana w aplikacjach komercyjnych.
Relacja R jest w tej postaci, jeśli jest w 1NF oraz dla każdej
nietrywialnej zależności ![]() zachodzącej w R, lewa strona
zależności
zachodzącej w R, lewa strona
zależności ![]() jest nadkluczem.
jest nadkluczem.
W odróżnieniu od 3NF sprowadzenie do BCNF nie gwarantuje zachowania zależności funkcyjnych przy rozkładzie.
Popatrzmy na inną definicję 3NF, lepiej pokazującą różnicę między nią a BCNF.
Definicja 6.8 (3NF)
Relacja jest w 3NF jeśli jest w 1NF oraz
dla każdej nietrywialnej zależności ![]() :
:
-
lewa strona zależności
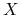 jest nadkluczem
jest nadkluczem -
lub
-
prawa strona zależności
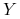 zawiera tylko atrybuty z kluczy
(bo kluczy może być kilka)
zawiera tylko atrybuty z kluczy
(bo kluczy może być kilka)
6.4.6. Dekompozycja do BCNF
Dekomponując relację R do BCNF pozbywamy się kolejno zależności naruszających ją. Przedtem należy zminimalizować zbiór zależności, ale pominiemy ten etap.
-
Dla relacji
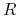 wybierz ze zbioru zależności
wybierz ze zbioru zależności 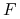 zależność
zależność
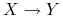 naruszającą BCNF (jeśli nie ma takiej, to relacja
jest już w BCNF).
naruszającą BCNF (jeśli nie ma takiej, to relacja
jest już w BCNF). -
Oblicz
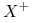
-
Będzie zawierać tylko część atrybutów
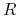 , bo inaczej
, bo inaczej 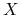 byłoby
nadkluczem.
byłoby
nadkluczem.
-
-
Zastąp
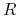 dwoma relacjami o schematach
dwoma relacjami o schematach -
-
Zrzutuj zbiór zależności
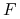 na nowe relacje.
na nowe relacje. -
Powtarzaj dopóki relacje nie będą w BCNF.
6.4.7. Zachowanie zależności
Czasem zależności powodują kłopoty przy przejściu do BCNF. Weźmy tabelę Gdzie(adres,miasto,kod-pocztowy) i dwie zależności
| adres miasto |
| kod-pocztowy |
Mamy tu dwa klucze: {adres,miasto} oraz {adres,kod-pocztowy}.
Ale zależność kod-pocztowy ![]() miasto
narusza postać BCNF, czyli musimy dokonać dekompozycji na dwie tabele
miasto
narusza postać BCNF, czyli musimy dokonać dekompozycji na dwie tabele
| Gdzie1(adres,kod-pocztowy) |
| Gdzie2(miasto,kod-pocztowy) |
Popatrzmy jednak na poniższy (ciut złośliwy) przykład
| Gdzie2 | |
|---|---|
| adres | kod |
| Banacha 2 | 01-234 |
| Banacha 2 | 01-235 |
| Gdzie1 | |
|---|---|
| miasto | kod |
| Warszawa | 01-234 |
| Warszawa | 01-235 |
Pozornie wszystko jest w porządku (żadna zależność nie jest naruszona), ale po złączeniu będzie już inaczej
| Gdzie | ||
|---|---|---|
| adres | miasto | kod |
| Banacha 2 | Warszawa | 01-234 |
| Banacha 2 | Warszawa | 01-235 |
Naruszona jest zależność
adres miasto ![]() kod-pocztowy.
kod-pocztowy.
Takie kłopotliwe układy zależności nie są rzadkie, popatrzmy na inny przykład zależności dla fikcyjnej sieci kin
| kino |
| film miasto |
Pierwsza z nich jest oczywista: każde kino znajduje się tylko w jednym mieście. Druga może wynikać z prowadzonej ,,polityki” wyświetlania, aby kina w tym samym mieście nie konkurowały ze sobą filmami. Skutek jest taki sam jak poprzednio.
6.5. Zależności wielowartościowe
6.5.1. Czwarta postać normalna (4NF)
W większości baz danych wystarcza dekompozycja do trzeciej postaci normalnej. Mogą jednak czasem występować anomalie wstawiania, powodowane zależnością wielowartościową.
Będzie tak między innymi wtedy, gdy pewne dwa niekluczowe atrybuty przyjmują dla każdej wartości innego atrybutu tylko po kilka wybranych wartości, niezależnie od innych atrybutów.
Na przykład na seminariach korzysta się z kilku książek. Każde seminarium ma tylko jedną nazwę, ale może mieć kilku prowadzących. Należy wówczas dokonać dekompozycji na dwie osobne relacje: prowadzący seminaria oraz teksty do seminariów, w przeciwnym razie wypadałoby umieścić w relacji dla danego seminarium wszystkie kombinacje prowadzących i książek.
Przykład zależności wielowartościowej
-
Tabela
Aktorzy(nazwisko,ulica,miasto,film,rok)
podaje adresy aktorów (mogą mieć kilka) i filmy, w których grali.
-
Każdy aktor mógł grać w wielu filmach i może mieć kilka adresów.
-
Ale w pojedynczym wierszu możemy zapisać tylko jeden film i jeden adres.
-
Trudno będzie wtedy znajdować wszystkie filmy aktorów mieszkających w Warszawie.
-
W zasadzie powinniśmy zapisać wszystkie kombinacje adresów z filmami.
Definicja zależności wielowartościowej
Definicja 6.9 (Zależność wielowartościowa)
Zależność wielowartościowa
dla relacji ![]() oznacza, że jeśli
dwie krotki są zgodne na składowych
oznacza, że jeśli
dwie krotki są zgodne na składowych ![]() , to można w nich zamienić
składowe
, to można w nich zamienić
składowe ![]() i otrzymane krotki będą także w relacji
i otrzymane krotki będą także w relacji ![]() .
.
-
Inaczej mówiąc, lewa strona każdej takiej zależności nie wyznacza pojedynczej wartości, lecz zbiór wartości, np.
nazwisko 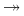 ulica,miasto
ulica,miastonazwisko 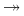 film,rok
film,rok
Reguły dla zależności wielowartościowych
Stwierdzenie 6.1 (Promocja)
Każda zależność funkcyjna jest
zależnością wielowartościową, czyli jeśli zachodzi
![]()
to zachodzi także
![]()
-
Niestety odwrotna implikacja nie jest prawdziwa!
Stwierdzenie 6.2 (Uzupełnianie)
Jeśli dla relacji ![]() zachodzi
zachodzi
![]()
to zachodzi także
![]()
Stwierdzenie 6.3 (Przechodniość)
Jeśli dla relacji ![]() zachodzą
zachodzą
![]()
![]()
to zachodzi także
![]()
Dodatkowe uwagi
-
Podobnie jak dla zależności funkcyjnych, nie wolno rozbijać lewej strony zależności.
-
Ale dla zależności wielowartościowych nie wolno również rozbijać prawej strony!
Czwarta postać normalna — definicja
Definicja 6.10 (Nietrywialna zależność wielowartościowa)
Zależność wielowartościowa ![]() dla relacji
dla relacji ![]() jest nietrywialna, jeśli
jest nietrywialna, jeśli
-
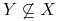 oraz
oraz -
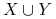 nie są wszystkimi atrybutami
nie są wszystkimi atrybutami 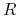
Definicja 6.11 (4NF)
Relacja ![]() jest w czwartej postaci normalnej (4NF), jeśli dla każdej
nietrywialnej zależności
jest w czwartej postaci normalnej (4NF), jeśli dla każdej
nietrywialnej zależności ![]() w
w ![]() ,
, ![]() jest nadkluczem
jest nadkluczem
![]() .
.
Wnioski
-
Jeśli relacja jest w 4NF, to jest też w BCNF.
-
Odwrotne zawieranie nie zachodzi.
Rozkład do 4NF
-
Podobnie jak dla BCNF, szukamy zależności
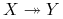 naruszającej 4NF.
naruszającej 4NF. -
Rozbijamy relację
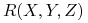 na dwie relacje:
na dwie relacje: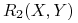
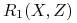
-
Kończymy, gdy już nie ma takich zależności.
Przykład rozkładu do 4NF
-
Zaczynamy od relacji Aktorzy(nazwisko,ulica,miasto,film,rok)
i zależności
nazwisko 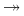 ulica,miasto
ulica,miastonazwisko 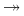 film,rok
film,rok -
W skład klucza wchodzą wszystkie kolumny tabeli.
-
Obie zależności naruszają więc 4NF (bo nie są trywialne).
-
Wybieramy do rozkładu pierwszą z nich.
-
Otrzymujemy dwie tabele
Aktorzy1(nazwisko,ulica,miasto) Aktorzy2(nazwisko,film,rok) z tymi samymi zależnościami.
-
Ponieważ obie zależności stały się trywialne, kończymy.
6.6. Zadania
Ćwiczenie 6.1
Czy któraś z podanych zależności funkcyjnych jest zależnością trywialną?
Pierwsza i trzecia.
Ćwiczenie 6.2
Dla relacji ![]() nie określono żadnych zależności
funkcyjnych. Relacja
nie określono żadnych zależności
funkcyjnych. Relacja ![]() :
:
-
nie ma żadnego klucza
-
ma jeden klucz
-
ma 4 klucze.
Ma jeden klucz, składający się z wszystkich atrybutów relacji.
Ćwiczenie 6.3
Ćwiczenie 6.4
Które z poniższych stwierdzeń są prawdziwe:
-
Każda relacja w 3NF jest także w BCNF.
-
Każda relacja w BCNF jest także w 3NF.
-
Każda relacja dwuargumentowa jest w BCNF.
Drugie i trzecie.
Ćwiczenie 6.5
Dana jest tabela ![]() z jedynymi zależnościami funkcyjnymi
z jedynymi zależnościami funkcyjnymi
Który z poniższych zbiorów atrybutów jest kluczem ![]() ?
?
Tylko ![]() .
.
Ćwiczenie 6.6
Dana jest tabela ![]() z jedynymi zależnościami funkcyjnymi
z jedynymi zależnościami funkcyjnymi
będąca w pierwszej postaci normalnej (1NF).
W jakich jeszcze postaciach jest ta tabela?
-
2NF
-
3NF
-
BCNF
2NF i 3NF.




