9. Programowanie w logice

9.1. Wprowadzenie

Programowanie w logice to jeden z paradygmatów współczesnego programowania. Programu przestaje być przepisem wykonania krok po kroku pewnego algorytmu, lecz jest traktowana jak teoria w logice.

W tym podejściu koncentrujemy się na deklaratywnym opisaniu, co ma być rozwiązane (odpowiednie postawienie problemu), a nie na szczegółowej proceduralnej specyfikacji, jak należy to rozwiązać.

Języki do programowania w logice są oparte na rachunku predykatów pierwszego rzędu, mają więc zdecydowany posmak relacyjny. W tym podejściu wywołanie procedury odpowiada podaniu twierdzenia do udowodnienia i jest często podawane interpreterowi jako zapytanie. Wykonanie programu oznacza poszukiwanie dowodu.

Jedną z konsekwencji tego podejścia jest specyficzne, typowe dla matematyki traktowanie zmiennych — mogą mieć one nadaną wartość tylko raz.

Najbardziej znanym językiem programowania w logice jest Prolog. Nie jest oczywiście możliwe nauczenie (ani nawet opisanie) Prologu w ramach jednego wykładu.

Pobieżne zaznajomienie się z koncepcjami programowania w logice pozwoli jednak zrozumieć, skąd wywodzi się koncepcja dedukcyjnych baz danych, o której opowiemy w następnym wykładzie. Operować będziemy głównie przykładami programów.

9.2. Warszawskie metro

Warszawskie metro ma (na razie) tylko jedną linię, ale w zupełności wystarczy to na pierwszy przykład użycia Prologu. Rozpoczniemy od zapisania faktów: informacji o kolejności stacji na linii.

connected(bielany,słodowiec).
connected(słodowiec,marymont).
connected(marymont,placWilsona).
connected(placWilsona,dworzecGdański).
  ...

Składnia nie jest skomplikowana. Prolog używa dla literałów składni pochodzącej z rachunku predykatów predykat(term,…term)

Nazwy zmiennych (identyfikatory) muszą rozpoczynać się wielką literą lub znakiem podkreślenia (`_')'. Identyfikator rozpoczynający się małą literą jest stałą — symbolem.

9.2.1. Zapytania

Prologu można używać jak prostej bazy danych. Możemy na przykład zapytać interpreter Prologu, czy Marymont i Plac Wilsona są ze sobą połączone.

| ?- connected(marymont,placWilsona).
yes

Następnie zapytamy o stacje połączone z Marymontem

| ?- connected(marymont,X).
X = placWilsona
yes

W zapytaniu użyliśmy zmiennej X. Interpreter zwrócił wartość związaną ze zmienną X jako jedyną odpowiedź.

Używając zmiennych możemy spytać o wszystkie połączenia

| ?- connected(Start,End).
Start = bielany
End = słodowiec ? ;
Start = słodowiec
End = marymont ? a
Start = marymont
End = placWilsona
Start = placWilsona
End = dworzecGdański
no

Interpreter, z którego pochodzą przykłady, po podaniu pierwszej odpowiedzi czeka na polecenie użytkownika. Naciśnięcie średnika to prośba o kolejną odpowiedź, zaś litera a (all) oznacza żądanie podania wszystkich pozostałych odpowiedzi.

9.3. Reguły

Zdefiniujmy dwie stacje jako położone blisko jeśli są one połączone bezpośrednio lub pomiędzy nimi jest tylko jedna stacja. W rachunku predykatów wygląda to tak

$\begin{array}[]{l}\forall x\forall y.connected(x,y)\implies blisko(x,y)\\ \forall x\forall y.\forall z.connected(x,z)\land connected(z,y))\implies blisko(x,y)\end{array}$

Tę samą informację można zapisać regułami Prologu

blisko(X,Y) :- connected(X,Y).
blisko(X,Y) :- connected(X,Y),connected(Y,Z).

Najpierw łatwe zapytanie
```
| ?- blisko(bielany,marymont).
yes
```

Teraz oczekujemy kilku odpowiedzi

| ?- blisko(bielany,What).
What = słodowiec ? ;
What = marymont
yes

9.4. Definiowanie silni

Wprowadzenie do języka programowania nie liczy się, jeśli nie obejmuje silni (albo największego wspólnego dzielnika). Pora więc na nią

Najpierw definicja funkcyjna

$\begin{array}[]{l}0!=1\\ n!=n\cdot(n-1)!\quad\mathrm{dla}\quad n>0.\end{array}$

którą przekształcimy na relację $factorial$

$\begin{array}[]{l}factorial(0,1)\\ (\forall n)(\forall f)n>0\land factorial(n-1,f)\implies factorial(n,n\cdot f)\end{array}$

factorial(0,1).
factorial(N,F) :-
   N > 0,
   N1 is N - 1,
   factorial(N1,F1),
   F is N * F1.

9.5. Klauzule

Program składa się z dwóch klauzul.
Pierwsza z nich to klauzula unarna: tylko nagłówek, bez treści. Jest to skrót następującego zapisu:
```
factorial(0,1) :- true.
```
Klauzule unarne bez zmiennych służą do zapisywania pojedynczych faktów.
Druga klauzula to reguła, ponieważ posiada niepustą treść.
Treść to wszystkie literały następujące po ':-' (możemy go czytać ,,jeśli”).
Literały w treści oddzielamy przecinkami, przecinek pełni rolę operatora koniunkcji.

Standardowo nazwy zmiennych rozpoczynają się dużymi literami.

Klauzule mają intepretację deklaratywną
- Klauzula pierwsza mówi: ,,silnia o wynosi 1”.
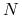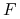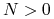- Klauzula druga mówi: ,,silnia $N$ wynosi $F$ jeśli $N>0$ oraz jeśli 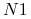$N1$ oznacza 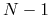$N-1$ , to silnia 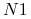$N1$ wynosi 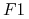$F1$ i $F=N*F1$ ”.

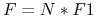9.6. Zapytania

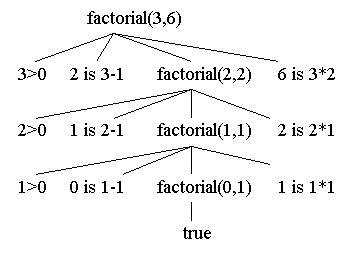
Chcąc obliczyć silnię od 3 musimy podać w zapytaniu zmienną, na której ma znaleźć się wynik — niech to będzie W:

?-  factorial(3,W).
W=6

Graf obliczeń

Rys. 9.1. .

W zapytaniu nie muszą wystąpić zmienne:

?- factorial(3,6).
yes
?- factorial(5,2).
no

Inna definicja silni

silnia(N,F) :- factorial(N,1,F).
factorial(0,F,F).
factorial(N,A,F) :-
    N > 0,
    A1 is N * A,
    N1 is N - 1,
    factorial(N1,A1,F).

Wprowadziliśmy drugi parametr pełniący rolę akumulatora.
Dzięki temu nasza definicja ma postać iteracyjną, ponieważ wywołanie rekurencyjne jest redukcyjne.
Płacimy za to zmniejszoną czytelnością.

9.7. Kolorowanie map

Zasada:

Żadne dwa sąsiadujące regiony nie mogą mieć tego samego koloru.

Rys. 9.2. Przykładowa mapa.

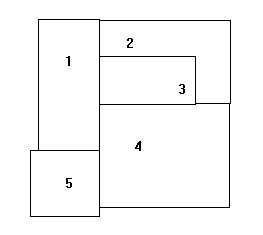
Sąsiedztwo

Informacje o sąsiedztwie można w Prologu zapisać następująco:

adjacent(1,2).         adjacent(2,1).
adjacent(1,3).         adjacent(3,1).
adjacent(1,4).         adjacent(4,1).
adjacent(1,5).         adjacent(5,1).
adjacent(2,3).         adjacent(3,2).
adjacent(2,4).         adjacent(4,2).
adjacent(3,4).         adjacent(4,3).
adjacent(4,5).         adjacent(5,4).

Po załadowaniu tych faktów do interpretera można badać sąsiedztwo regionów:

?- adjacent(2,3).
yes
?- adjacent(5,3).
no
?- adjacent(3,R).
R = 1 ;
R = 2 ;
R = 4 ;
no

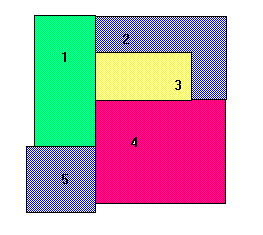
Kolorowania

Kolorowania także możemy opisać klauzulami unarnymi.

color(1,red,a).     color(1,red,b).
color(2,blue,a).    color(2,blue,b).
color(3,green,a).   color(3,green,b).
color(4,yellow,a).  color(4,blue,b).
color(5,blue,a).    color(5,green,b).

Kolorowania oznaczyliśmy symbolami a i b.

Rys. 9.3. Kolorowania.

Konflikty

Błędne kolorowanie musi zawierać konflikt — dwa sąsiednie regiony pokolorowane tym samym kolorem:

conflict(Coloring) :-
   adjacent(X,Y),
   color(X,Color,Coloring),
   color(Y,Color,Coloring).

Teraz możemy zbadać nasze kolorowania:

?- conflict(a).
no
?- conflict(b).
yes
?- conflict(Which).
Which = b

Konfliktowość mozna też zdefiniować inaczej:

conflict(R1,R2,Coloring) :-
   adjacent(R1,R2),
   color(R1,Color,Coloring),
   color(R2,Color,Coloring).

Polimorfizm

Prolog dopuszcza równoczesne definiowanie predykatów o tej samej nazwie i różnej liczbie parametrów, wewnętrznie nazywając je 'conflict/1' i 'conflict/3'.

Więcej o konfliktach

Możemy poznać konfliktowe regiony, a nawet ich (wspólny) kolor

?- conflict(R1,R2,b).
R1 = 2   R2 = 4
?- conflict(R1,R2,b),color(R1,C,b).
R1 = 2   R2 = 4   C = blue

9.8. Rozpoznawanie zwierząt

Na koniec obejrzymy przykład programu do identyfikacji zwierząt na podstawie zaobserwowanych cech. Program korzysta z własnej ,,bazy danych”, zawierającej informacje o cechach poszczególnych gatunków. Przypominamy, że nazwy zmiennych w klauzulach rozpoczynają się dużymi literami (lub podkreśleniem).

zoolog :- hypothesize(Zwierzak),
      write('Przypuszczam, że ten zwierzak to: '),
      write(Zwierzak),
      nl,
      undo.

write i nl to przykłady pozalogicznych predykatów obliczalnych, wywołujących rozmaite akcje — w tym przypadku służących do wypisywania.

9.8.1. Hipotezy

Predykat hypothesisze określa możliwe hipotezy — gatunki, które jesteśmy w stanie rozpoznawać.

hypothesize(gepard)   :- gepard, !.
hypothesize(tygrys)   :- tygrys, !.
hypothesize(żyrafa)   :- żyrafa, !.
hypothesize(zebra)    :- zebra, !.
hypothesize(struś)    :- struś, !.
hypothesize(pingwin)  :- pingwin, !.
hypothesize(albatros) :- albatros, !.
hypothesize(nie_wiem).    /* nie udało się */

Specjalny predykat wbudowany ! to tzw. odcięcie. Powoduje on, po udanym dojściu do niego, pominięcie pozostałych gałęzi (czyli klauzul) predykatu hypothesisze. W tym przypadku po rozpoznaniu jednego z gatunków nie próbujemy już rozpoznawać innych.

9.8.2. Reguły identyfikacji

Reguły identyfikacji zrealizujemy bezargumentowymi predykatami nazwanyni nazwami gatunków.

gepard :- ssak,
          drapieżnik,
          verify(ma_płowy_kolor),
          verify(ma_ciemne_plamy).
tygrys :- ssak,
          drapieżnik,
          verify(ma_płowy_kolor),
          verify(ma_czarne_paski).
żyrafa :- kopytny,
          verify(ma_długą_szyję),
          verify(ma_długie_nogi).
zebra :- kopytny,
         verify(ma_czarne_paski).
struś :- ptak,
         verify(nie_lata),
         verify(ma_długą_szyję).
pingwin :- ptak,
           verify(nie_lata),
           verify(pływa),
           verify(jest_czarnobiały).
albatros :- ptak,
            verify(występuje_w_opowieściach_morskich),
            verify(dobrze_lata).

9.8.3. Reguły klasyfikacji

Reguły klasyfikacji pozwalają nam zapisać wspólną informację tylko w jednym miejscu, unikając dublowania informacji.

ssak       :- verify(ma_sierść), !.
ssak       :- verify(daje_mleko).
ptak       :- verify(ma_pióra), !.
ptak       :- verify(lata),
              verify(znosi_jajka).
drapieżnik :- verify(je_mięso), !.
drapieżnik :- verify(ma_ostre_zęby),
              verify(ma_pazury),
              verify(ma_oczy_z_przodu).
kopytny :- ssak,
           verify(ma_kopyta), !.
kopytny :- ssak,
           verify(przeżuwacz).

9.8.4. Zadawanie pytań

Prostą obsługę dialogu z użytkownikiem nie jest trudno zapisać bezpośrednio w Prologu.

ask(Pytanie) :-
    write('Czy zwierzak ma następującą cechę: '),
    write(Pytanie),
    write('? '),
    read(Odpowiedz),
    nl,
    ( (Odpowiedz == tak ; Odpowiedz == t)
      ->
       assert(tak(Pytanie)) ;
       assert(nie(Pytanie)), fail).

Aby uniknąć wielokrotonego zadawania tych samych pytań odpowiedzi będziemy zapamiętywać. Po otrzymaniu odpowiedzi tak na pytanie $P$ zapisujemy tę informację jako fakt tak( $S$ ).

Podobnie po otrzymaniu odpowiedzi nie na pytanie $P$ zapisujemy tę informację jako fakt nie( $S$ ).

Wbudowany predykat fail powoduje niepowodzenie (nigdy nie może być ,,udowodniony”) i konieczność wycofania się z danej gałęzi.

Predykat verify zagląda najpierw do bazy faktów, a dopiero potem ewentualnie zadaje pytanie użytkownikowi.

verify(S) :- tak(S), true, !.
verify(S) :- nie(S), fail, !.
verify(S) :- ask(S).

Po rozpoznaniu :-(lub nie) kolejnego zwierzaka bazę faktów tak/nie należy oczyścić

undo :- retract(tak(_)), fail.
undo :- retract(nie(_)), fail.
undo.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Bazy danych

Zagadnienia