Zagadnienia
10. Teoria dużej próbki cd
10.1. Testy asymptotyczne
10.1.1. Testowanie pojedynczego parametru strukturalnego 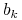
Przyjmujemy założenia Z̃1 – Z̃6. Wówczas dwa poniższe ciągi mają tą samą granicę:
Zatem dla pojedynczej współrzędnej otrzymujemy
Oznaczenie. Błąd standardowy estymatora ![]() będziemy oznaczać przez
będziemy oznaczać przez ![]()
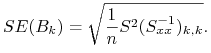 |
Testujemy hipotezę ![]() wobec hipotezy alternatywnej
wobec hipotezy alternatywnej
![]() , gdzie
, gdzie ![]() ustalona liczba rzeczywista.
ustalona liczba rzeczywista.
Jako statystykę testową przyjmujemy stosunek odchylenia estymatora od wartości testowej i błędu standardowego estymatora
Twierdzenie 10.1
Przy założeniach Z̃1 – Z̃6 i ![]()
Dowód.
Ponieważ ![]() zbiega według rozkładu do
zbiega według rozkładu do ![]() a
a ![]() prawie napewno do
prawie napewno do ![]() , to otrzymujemy
, to otrzymujemy
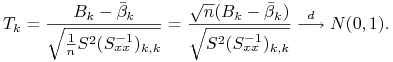 |
Reguła decyzyjna dla zadanego poziomu istotności ![]() .
.
1. Na podstawie próbki ![]() wyznaczamy realizację statystyki testowej
wyznaczamy realizację statystyki testowej ![]() .
.
2. Wyznaczamy wartość krytyczną ![]() jako kwantyl rozkładu normalnego
jako kwantyl rozkładu normalnego
gdzie ![]() oznacza dystrybuantę rozkładu
oznacza dystrybuantę rozkładu ![]() .
.
3. Jeżeli ![]() to nie ma podstaw do odrzucenia hipotezy
to nie ma podstaw do odrzucenia hipotezy ![]() .
.
Jeżeli ![]() to odrzucamy
to odrzucamy ![]() na rzecz
na rzecz ![]() .
.
Uwaga.
Powyższa reguła jest zgodna z regułami przedstawionymi w rozdziale 5.1, gdyż rozkład t-Studenta wraz ze wzrostem liczby stopni swobody zbiega do standardowego rozkładu normalnego
10.1.2. Testowanie hipotezy liniowości
Zajmiemy sie teraz testowaniem hipotezy, że nieznany parametr ![]() spełnia
spełnia ![]() niezależnych warunków liniowych.
Czyli, że należy do podprzestrzeni afinicznej kowymiaru
niezależnych warunków liniowych.
Czyli, że należy do podprzestrzeni afinicznej kowymiaru ![]() .
.
Niech ![]() macierz o współczynnikach rzeczywistych wymiaru
macierz o współczynnikach rzeczywistych wymiaru ![]() , rzędu
, rzędu ![]() , gdzie
, gdzie ![]() ,
a
,
a ![]() wektor kolumnowy wymiaru
wektor kolumnowy wymiaru ![]() .
Testujemy hipotezę
.
Testujemy hipotezę
wobec
Jako statystykę testową przyjmujemy statystykę Walda
Twierdzenie 10.2
Przy założeniach Z̃1 – Z̃6 i ![]()
gdzie ![]() oznacza rozkład chi-kwadrat z
oznacza rozkład chi-kwadrat z ![]() stopniami swobody.
stopniami swobody.
Dowód.
Zapiszemy statystykę ![]() jako
jako
gdzie
Hipoteza zerowa ![]() implikuje, że
implikuje, że ![]() i
i
Zatem (Tw. 9.1 b.)
Natomiast ![]() zbiega do pewnej macierzy deterministycznej
zbiega do pewnej macierzy deterministycznej ![]() (Tw. 9.1 d.)
(Tw. 9.1 d.)
Ponieważ asymptotyczna macierz wariancji ![]() jest dodatnio określona, a wiersze macierzy
jest dodatnio określona, a wiersze macierzy ![]() są liniowo niezależne (macierz
są liniowo niezależne (macierz ![]() ma rząd
ma rząd ![]() ),
to
),
to ![]() macierz
macierz ![]() jest odwracalna (jest to macierz Grama wierszy macierzy
jest odwracalna (jest to macierz Grama wierszy macierzy ![]() ).
Zatem przechodząc do granicy otrzymujemy
).
Zatem przechodząc do granicy otrzymujemy
Uwaga 10.1
Zauważmy, że statystyka Walda daje się wyrazić przez F-statystykę stosowaną w modelu klasycznym (Tw. 5.2)
W przypadku gdy spełnione są zarówno aksjomaty modelu klasycznego jak i modelu dużej próbki, to
oba podejścia są zgodne. Rzeczywiście gdy ![]() , to
, to
a zatem
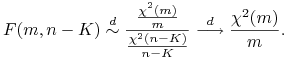 |
Uwaga 10.2
Podobnie jak w modelu klasycznym możemy wyrazić statystykę ![]() za pomocą sum kwadratów reszt.
Niech
za pomocą sum kwadratów reszt.
Niech ![]() suma kwadratów reszt dla modelu spełniającego ograniczenie
suma kwadratów reszt dla modelu spełniającego ograniczenie ![]() . Wówczas
. Wówczas
Uwaga 10.3
W modelu z wyrazem stałym (![]() ) współczynnik determinacji daje się wyrazić za pomocą statystyki
) współczynnik determinacji daje się wyrazić za pomocą statystyki ![]() wyznaczonej dla
wyznaczonej dla ![]() warunków
warunków ![]() ,
,
Zatem, po przejściu z ![]() do granicy otrzymujemy
do granicy otrzymujemy
10.1.3. Testowanie nieliniowych zależności między parametrami modelu
Metoda delty (Tw. 8.4) pozwala uogólnić test Walda na przypadek zależności nieliniowych.
Niech ![]() oznacza submersję
oznacza submersję
tzn. odwzorowanie klasy ![]() o maksymalnym rzędzie pochodnej
o maksymalnym rzędzie pochodnej
Dla ustalenia uwagi przyjmiemy, że ![]() jest wektorem kolumnowym.
jest wektorem kolumnowym.
Będziemy testować hipotezę
wobec hipotezy alternatywnej
Jako statystykę testową przyjmujemy statystykę Walda
Twierdzenie 10.3
Przy założeniach Z̃1 – Z̃6 i ![]()
gdzie ![]() oznacza rozkład chi-kwadrat z
oznacza rozkład chi-kwadrat z ![]() stopniami swobody.
stopniami swobody.
Dowód.
Z twierdzenia o odwzorowaniu ciągłym (Tw. 8.2) i założenia ![]() otrzymujemy, że
otrzymujemy, że
Zatem możemy zastosować metodę delty (Tw. 8.4)
Z założeń modelowych wynika, że
a z twierdzenia o odwzorowaniu ciągłym, że
Z powyższego wynika, że
Ponieważ macierz pochodnych ma rząd ![]() to
to ![]() macierz
macierz ![]() jest odwracalna.
Zatem statystyka
jest odwracalna.
Zatem statystyka ![]() jest dobrze zdefiniowana i
jest dobrze zdefiniowana i
10.1.4. Testowanie warunkowej homoskedastyczności – test White'a
Rozważamy model liniowy
gdzie ![]() jest
jest ![]() wymiarowym wektorem wierszowym.
wymiarowym wektorem wierszowym.
Niech
wektor złożony z wybranych elementów ![]() macierzy
macierzy ![]() ,
, ![]() i wyrazu stałego.
Załóżmy, że proces
i wyrazu stałego.
Załóżmy, że proces ![]() spełnia warunki Z̃1 – Z̃6 modelu dużej próbki,
w szczególności, że istnieją wektor
spełnia warunki Z̃1 – Z̃6 modelu dużej próbki,
w szczególności, że istnieją wektor ![]() i składnik losowy
i składnik losowy ![]() takie, że
takie, że
Testujemy hipotezę
wobec hipotezy alternatywnej
W teście White reguła decyzyjna opiera się na fakcie, że przy załóżeniu ![]()
gdzie ![]() współczynnik determinacji wyznaczony dla modelu pomocniczego
współczynnik determinacji wyznaczony dla modelu pomocniczego
w którym
składnik losowy ![]() zastąpiono składnikiem resztowym
zastąpiono składnikiem resztowym ![]() z metody MNK.
z metody MNK.




