Zagadnienia
13. Regresja względem czasu.
Teoria dużej próbki cd. Model tendencji rozwojowej z liniowym trendem. Estymatory hiper-zgodne.
13.1. Model tendencji rozwojowej z liniowym trendem
13.1.1. Założenia modelu
Rozważamy następujący model liniowy
| (13.1) |
gdzie![]() – czas (kolejny moment),
– czas (kolejny moment), ![]() (lub
(lub ![]() ),
),![]() – niezależny, biały szum; tzn.
– niezależny, biały szum; tzn. ![]() nie zależą od historii i mają ten sam rozkład.
Ponadto zakładamy, że
nie zależą od historii i mają ten sam rozkład.
Ponadto zakładamy, że ![]() ,
, ![]() oraz
oraz ![]() .
.
Przyjmiemy następujące oznaczenia
Wówczas model 13.1 można zapisać w następujący sposób
W zapisie macierzowym otrzymamy
Powyższy model spełnia założenia modelu klasycznego Z1 – Z4 (bez założenia o normalności składnika losowego)
i nie spełnia założeń modelu ”dużej próbki”, bo proces ![]() nie jest stacjonarny.
nie jest stacjonarny.
Problem.
Co można powiedzieć o asymptotyce estymatorów MNK dla modelu opisanego równaniem 13.1?
13.1.2. Estymacja parametrów modelu
Rozważmy proces generujący dane ![]() , z którego bierzemy
, z którego bierzemy
![]() -elementową próbkę dla
-elementową próbkę dla ![]() .
MNK estymator wektora
.
MNK estymator wektora ![]() wyznaczamy ze wzoru
wyznaczamy ze wzoru
gdzie
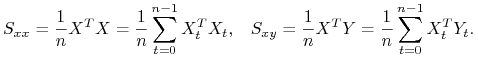 |
Natomiast MNK estymator wariancji ![]() wynosi
wynosi
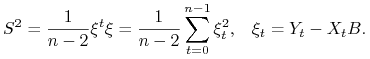 |
Twierdzenie 13.1
![\left(\begin{array}[]{c}\sqrt{n}^{{3}}(B_{1}-\beta _{1})\\
\sqrt{n}(B_{2}-\beta _{2})\end{array}\right)\stackrel{d}{\longrightarrow}N(0,\sigma^{2}\Sigma),\;\;\;\Sigma=\left(\begin{array}[]{rr}12&-6\\
-6&4\end{array}\right).](wyklady/ekn/mi/mi1219.png) |
Dowód.
Zauważmy, że
gdzie
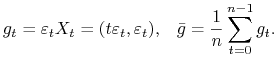 |
Macierz ![]() można łatwo wyliczyć
można łatwo wyliczyć
![S_{{xx}}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}X_{t}^{T}X_{t}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}\left(\begin{array}[]{c}t\\
1\end{array}\right)\circ(t,1)=](wyklady/ekn/mi/mi1491.png) |
![=\frac{1}{n}\sum _{{t=0}}^{{n-1}}\left(\begin{array}[]{cc}t^{2}&t\\
t&1\end{array}\right)=\left(\begin{array}[]{cc}\frac{(n-1)(2n-1)}{6}&\frac{n-1}{2}\\
\frac{n-1}{2}&1\end{array}\right).](wyklady/ekn/mi/mi1190.png) |
Gdy ![]() rośnie do nieskończoności to 3 wyrazy macierzy
rośnie do nieskończoności to 3 wyrazy macierzy ![]() zbiegają do nieskończoności
zbiegają do nieskończoności
![\left(\begin{array}[]{cc}\frac{(n-1)(2n-1)}{6}&\frac{n-1}{2}\\
\frac{n-1}{2}&1\end{array}\right)\longrightarrow\left(\begin{array}[]{cc}\infty&\infty\\
\infty&1\end{array}\right).](wyklady/ekn/mi/mi1208.png) |
Aby uzyskać rodzine macierzy o skończonej granicy pomnożymy macierz ![]() z obu stron przez macierz diagonalną
z obu stron przez macierz diagonalną
Otrzymujemy
![\Phi _{n}S_{{xx}}\Phi _{n}=\left(\begin{array}[]{cc}\frac{(n-1)(2n-1)}{6n^{2}}&\frac{n-1}{2n}\\
\frac{n-1}{2n}&1\end{array}\right)\longrightarrow Q,](wyklady/ekn/mi/mi1186.png) |
gdzie
Z drugiej strony z centralnego twierdzenia granicznego Linderberga-Levy'ego ([9] §10.2 Twierdzenie 1) otrzymujemy
asymptotyczną normalność ![]()
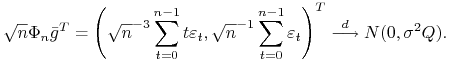 |
Podsumowując
![\left(\begin{array}[]{c}\sqrt{n}^{{3}}(B_{1}-\beta _{1})\\
\sqrt{n}(B_{2}-\beta _{2})\end{array}\right)=\sqrt{n}\Phi _{n}^{{-1}}(B-\beta)=\sqrt{n}\Phi _{n}^{{-1}}S_{{xx}}^{{-1}}\bar{g}^{T}=](wyklady/ekn/mi/mi1216.png) |
Ponieważ macierze
![]() zbiegają do
zbiegają do ![]() , a proces
, a proces ![]() zbiega według rozkładu do
zbiega według rozkładu do
![]() to
to
![\left(\begin{array}[]{c}\sqrt{n}^{{3}}(B_{1}-\beta _{1})\\
\sqrt{n}(B_{2}-\beta _{2})\end{array}\right)\stackrel{d}{\longrightarrow}N(0,\sigma^{2}Q^{{-1}}QQ^{{-1}})=N(0,\sigma^{2}Q^{{-1}}).](wyklady/ekn/mi/mi1192.png) |
Aby zakończyć dowód wystarczy zauważyć, że
Uwaga 13.1
Estymator ![]() nazywa się estymatorem
nazywa się estymatorem ![]() -zgodnym albo hiper-zgodnym (hyper-consistent).
-zgodnym albo hiper-zgodnym (hyper-consistent).
Twierdzenie 13.2
Estymator ![]() jest zgodny
jest zgodny
Dowód.
Jak pokazaliśmy w rozdziale 4 (patrz równanie 4.3)
gdzie ![]() macierz rzutu na dopełnienie ortogonalne podprzestrzeni rozpiętej przez kolumny macierzy
macierz rzutu na dopełnienie ortogonalne podprzestrzeni rozpiętej przez kolumny macierzy ![]()
Zatem
Stosując notację i oszacowania z dowodu poprzedniego twierdzenia otrzymujemy
13.1.3. Testowanie parametrów strukturalnych
Dla ![]() testujemy hipotezę
testujemy hipotezę
wobec hipotezy alternatywnej
Analogicznie jak w modelu klasycznym przyjmujemy
gdzie
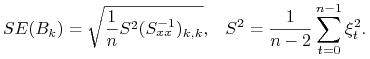 |
Twierdzenie 13.3
Przy założeniu hipotezy zerowej ![]() rozkład statystyki
rozkład statystyki ![]() zbiega do N(0,1).
zbiega do N(0,1).
Dowód.
Korzystamy z faktu, że ![]() zbiega do
zbiega do ![]() ,
, ![]() do
do ![]() ,
a
,
a ![]() do
do ![]() .
.
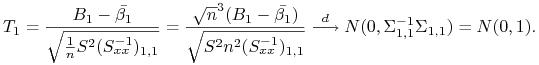 |
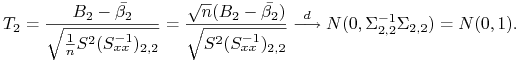 |




