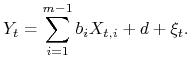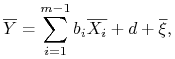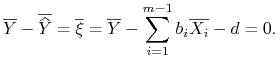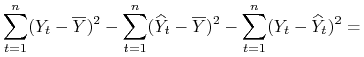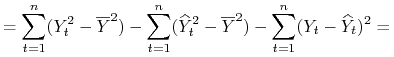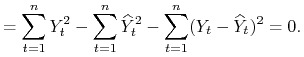3. MNK w terminach statystyki opisowej
Metoda MNK dla modeli z wyrazem wolnym. Współczynnik determinacji. Przypadek ![]() . (1 wykład)
. (1 wykład)
3.1. Notacja statystyki opisowej
Będziemy stosowali następującą notację:
Dla pojedynczej serii danych ![]() :
:![]() średnia
średnia
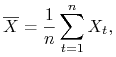 |
![]() wariancja empiryczna (wariancja z próby)
wariancja empiryczna (wariancja z próby)
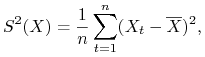 |
![]() empiryczne odchylenie standardowe (odchylenie standardowe z próby)
empiryczne odchylenie standardowe (odchylenie standardowe z próby)
Dla dwóch serii danych ![]() i
i ![]() :
:![]() kowariancja empiryczna (kowariancja z próby)
kowariancja empiryczna (kowariancja z próby)
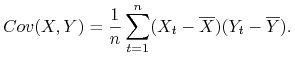 |
Uwaga 3.1
Zachodzą następujące związki
![]() współczynnik korelacji Pearsona (korelacja empiryczna)
współczynnik korelacji Pearsona (korelacja empiryczna)
Uwaga 3.2
Zachodzą następujące związki
Dla ![]() serii danych
serii danych ![]() ,
, ![]() :
:![]() macierz kowariancji serii
macierz kowariancji serii ![]() :
:
gdzie ![]() jest
jest ![]() macierzą o współczynnikach
macierzą o współczynnikach ![]() ,
a
,
a ![]() wektorem horyzontalnym o
wektorem horyzontalnym o ![]() wyrazach (tzn. macierzą
wyrazach (tzn. macierzą ![]() )
a
)
a ![]() wektorem kolumnowym o
wektorem kolumnowym o ![]() wyrazach (tzn. macierzą
wyrazach (tzn. macierzą ![]() )
)
Uwaga 3.3
Macierz ![]() jest symetryczna i nieujemnie określona. Ponadto
jest symetryczna i nieujemnie określona. Ponadto
Dla ![]() serii danych
serii danych ![]() ,
, ![]() i
i ![]() :
:![]() macierz kowariancji serii
macierz kowariancji serii ![]() i serii
i serii ![]() ,
, ![]() :
:
Uwaga 3.4
Zachodzą następujące związki
3.2. MNK z wyrazem wolnym
Rozważmy przypadek gdy jeden z ciągów ![]() ,
, ![]() jest stały.
Dla uproszczenia przyjmijmy
jest stały.
Dla uproszczenia przyjmijmy ![]() (tzn.
(tzn. ![]() ).
Wówczas dla wszystkich
).
Wówczas dla wszystkich ![]()
gdzie ![]() nazywamy wyrazem wolnym. W zapisie macierzowym wygląda to następująco
nazywamy wyrazem wolnym. W zapisie macierzowym wygląda to następująco
gdzie ![]() jest
jest ![]() macierzą o kolumnach
macierzą o kolumnach ![]() a
a ![]() .
Zatem suma kwadratów reszt wyniesie
.
Zatem suma kwadratów reszt wyniesie
Twierdzenie 3.1
Jeżeli ciągi ![]() są liniowo niezależne to
są liniowo niezależne to ![]() przyjmuje minimum w punkcie
przyjmuje minimum w punkcie
Ponadto
Dowód.
Krok 1. Pokażemy, że macierz ![]() jest dodatnio określona a zatem odwracalna.
jest dodatnio określona a zatem odwracalna.
Rozważmy dowolny niezerowy wektor ![]() . Wektor
. Wektor ![]() nie jest stały, zatem
nie jest stały, zatem
Krok 2.
Korzystając ze wzoru na ![]() wyprowadzonego w twierdzeniu 2.1 wyznaczymy
wyprowadzonego w twierdzeniu 2.1 wyznaczymy ![]() i
i ![]() .
.![]() spełnia zależność
spełnia zależność
Korzystając z faktu, że ![]() (tzn. macierz
(tzn. macierz ![]() powstaje z
powstaje z ![]() przez dopisanie kolumny jedynek)
a
przez dopisanie kolumny jedynek)
a ![]() ,
zapiszemy ją w terminach
,
zapiszemy ją w terminach ![]() ,
, ![]() i
i ![]()
![\left(\begin{array}[]{cc}X^{{\prime T}}X^{{\prime}}&n\overline{X^{{\prime}}}^{T}\\
n\overline{X^{{\prime}}}&n\end{array}\right)\circ\left(\begin{array}[]{c}B^{{\prime}}_{{min}}\\
d_{{min}}\end{array}\right)=\left(\begin{array}[]{c}X^{{\prime T}}Y\\
n\overline{Y}\end{array}\right).](wyklady/ekn/mi/mi167.png) |
Dzielimy obie strony przez ![]()
Z drugiego równania otrzymujemy formułę na ![]() , a następnie eliminujemy
, a następnie eliminujemy ![]() z pierwszego równania.
Po uporządkowaniu składników otrzymujemy
z pierwszego równania.
Po uporządkowaniu składników otrzymujemy
Co możemy zapisać w postaci (patrz uwagi 3.3 i 3.4)
Krok 3.
Wyznaczamy ![]() .
.
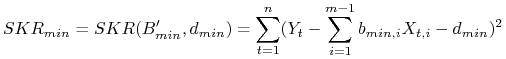 |
Po podstawieniu ![]() otrzymujemy
otrzymujemy
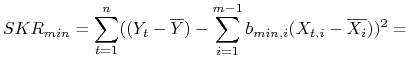 |
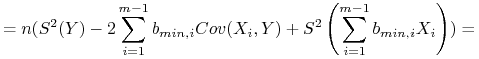 |
Uwaga 3.5
Dla ![]() i
i ![]() zachodzą następujące związki:
zachodzą następujące związki:
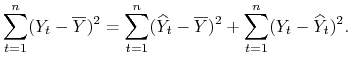 |
Definicja 3.1
Współczynnik determinacji zwany też współczynnikiem dopasowania i współczynnikiem regresji wielorakiej to
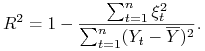 |
Uwaga 3.6
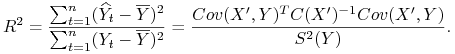 |
Definicja 3.2
Średni błąd kwadratowy
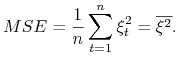 |
Uwaga 3.7
Podsumowanie.![]() i
i ![]() określają dokładność aproksymacji przy zastosowaniu metody najmniejszych kwadratów (MNK).
określają dokładność aproksymacji przy zastosowaniu metody najmniejszych kwadratów (MNK).
3.3. Przypadek 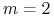 i
i 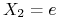
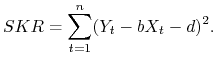 |
Twierdzenie 3.2
Jeżeli ciąg ![]() nie jest stały to
nie jest stały to ![]() przyjmuje minimum w punkcie
przyjmuje minimum w punkcie
Dowód.
Zamieniamy rolami ![]() i
i ![]() .
.
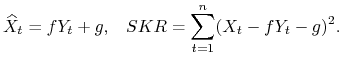 |
Otrzymujemy
Okazuje się, że proste ![]() i
i ![]() na ogół nie pokrywają się. Przecinają się one w punkcie
na ogół nie pokrywają się. Przecinają się one w punkcie ![]() i iloczyn współczynników kierunkowych wynosi
i iloczyn współczynników kierunkowych wynosi ![]()