Zagadnienia

4.1 Notacja macierzowa dla zmiennych losowych
4.2 Warunkowa wartość oczekiwana
4.3 Założenia klasycznego modelu regresji
4.4 Estymacja parametrów modelu metodą MNK

4. Klasyczny model regresji

Klasyczny jednorównaniowy liniowy model ekonometryczny. Założenia modelu. Estymacja parametrów strukturalnych modelu metodą najmniejszych kwadratów (regresja wieloraka). (1 wykład)

4.1. Notacja macierzowa dla zmiennych losowych

Definicja 4.1

Niech $X$ będzie $m\times n$ macierzą losową, której wyrazami są zmienne losowe $X_{{i,j}}$ określone na tej samej przestrzeni probabilistycznej. Wartością oczekiwaną $X$ będziemy nazywać $m\times n$ macierz $E(X)$ taką, że

$E(X)_{{i,j}}=E(X_{{i,j}}).$

Uwaga 4.1

Wartość oczekiwana macierzy jest zgodna z transpozycją

$E(X^{T})=E(X)^{T}$

oraz z mnożeniem przez macierze deterministyczne

$E(AXB)=AE(X)B,$

gdzie $A$ i $B$ macierze o współczynnikach rzeczywistych odpowiednio wymiaru $k\times m$ i $n\times p$ .

Definicja 4.2

Niech $X$ będzie $m\times 1$ macierzą losową (wektorem kolumnowym), której wyrazami są zmienne losowe $X_{{i}}$ określone na tej samej przestrzeni probabilistycznej. Macierzą kowariancji $X$ będziemy nazywać $m\times m$ macierz $Var(X)$

$Var(X)=E((X-E(X))(X-E(X))^{T}).$

Uwaga 4.2

Zachodzą następujące związki

$Var(X)=E(XX^{T})-E(X)E(X)^{T},$

$Var(X)_{{i,i}}=D^{2}(X_{i}),\;\;\; Var(X)_{{i,j}}=Cov(X_{i},X_{j}).$

$Var(X)$ jest macierzą symetryczną

$Var(X)^{T}=Var(X).$

Ponadto dla deterministycznej $k\times m$ macierzy $A$

$Var(AX)=AVar(X)A^{T}.$

Definicja 4.3

Niech $X$ i $Y$ będą wektorami kolumnowymi, których wyrazami są zmienne losowe $X_{{i}}$ , $i=1,\dots,m_{1}$ i $Y_{j}$ , $j=1,\dots,m_{2}$ określone na tej samej przestrzeni probabilistycznej. Macierzą kowariancji $X$ i $Y$ będziemy nazywać $m_{1}\times m_{2}$ macierz $Cov(X,Y)$

$Cov(X,Y)=E((X-E(X))(Y-E(Y))^{T}).$

Uwaga 4.3

Zachodzą następujące związki

$Cov(X,Y)=E(XY^{T})-E(X)E(Y)^{T},$

$Cov(X,Y)_{{i,j}}=Cov(X_{i},Y_{j}),$

$Cov(Y,X)=Cov(X,Y)^{T}.$

Ponadto dla deterministycznych $k\times m_{1}$ macierzy $A$ i $p\times m_{2}$ $B$

$Cov(AX,BY)=ACov(X,Y)B^{T}.$

4.2. Warunkowa wartość oczekiwana

Niech $(\Omega,{\cal M},P)$ będzie przestrzenią probabilistyczną, $\cal F$ $\sigma$ -ciałem zawartym w $\cal M$ a $Y$ zmienną losową określoną na $(\Omega,{\cal M},P)$ .

Definicja 4.4

Warunkową wartością oczekiwaną $Y$ pod warunkiem $\cal F$ nazywamy każdą zmienną losową $E(Y|{\cal F})$ o wartościach w $\mathbb{R}\cup\{\pm\infty\}$ spełniającą warunki:
i) $E(Y|{\cal F})$ jest $\cal F$ mierzalna;
ii) Dla każdego $A\in{\cal F}$

$\int _{A}YdP=\int _{A}E(Y|{\cal F})dP.$

Lemat 4.1

Każdy z poniższych warunków implikuje istnienie warunkowej wartości oczekiwanej $E(Y|{\cal F})$ .
1. $E(Y)$ jest określona (tzn. skończona lub nieskończona).
2. $Y$ należy do $L^{1}(\Omega,{\cal M},P)$ .
3. $Y\geq 0$ p.n. lub $Y\leq 0$ p.n.

Uwaga 4.4

Warunkowa wartość oczekiwana ma następujące własności:
1. $Y\geq 0$ p.n. to $E(Y|{\cal F})\geq 0$ p.n.
2. $E(1|{\cal F})=1$ p.n.
3. $E(Y_{1}+Y_{2}|{\cal F})=E(Y_{1}|{\cal F})+E(Y_{2}|{\cal F})$ o ile prawa strona jest określona (tzn. różna od $\infty-\infty$ ),
4. Jeżeli zmienna losowa $\xi$ jest $\cal F$ mierzalna i wartość oczekiwana $E(\xi Y)$ jest określona to

$E(\xi Y|{\cal F})=\xi E(Y|{\cal F}).$

5. Jeżeli wartość oczekiwana $E(Y)$ jest określona to dla dowolnego $\sigma$ -ciała $\cal G$ zawartego w $\cal F$

$E(Y|{\cal G})=E(E(Y|{\cal F})|{\cal G})\mbox{ p.n.}$

W szczególności

$E(Y)=E(E(Y|{\cal F})).$

4.3. Założenia klasycznego modelu regresji

W modelu regresji rozważa się zmienną objaśnianą (zależną, zwaną też regressandem) - $Y$ i zmienne objaśniające (zwane regressorami) - $X_{1},\dots,X_{K}$ .

Dysponujemy próbką złożoną z $n$ obserwacji. $i$ -tą obserwację modelujemy jako realizację $K+1$ wymiarowej zmiennej losowej

$(Y_{i},X_{{i,1}},\dots,X_{{i,K}}),\;\;\; i=1,\dots,n.$

Przez model rozumie się łączny rozkład zmiennych losowych $Y_{i}$ i $X_{{i,k}}$ spełniający pewne założenia.

Założenia modelu.

Z1. Liniowość.
Zmienne losowe $Y_{i}$ i $X_{{i,k}}$ należą do $L^{2}$ i spełniają zależność

$Y_{i}=\beta _{1}X_{{i,1}}+\dots+\beta _{K}X_{{i,K}}+\varepsilon _{i},\;\;\; i=1,\dots,n,$

gdzie $\beta _{i}\in\mathbb{R}$ to deterministyczne choć na ogół nieznane parametry regresji zwane też parametrami strukturalnymi modelu, zaś zmienne losowe $\varepsilon _{i}$ to składniki losowe. Funkcję

$f(x)=\beta _{1}x_{1}+\beta _{2}x_{2}+\dots+\beta _{K}x_{K},\;\;\; x\in\mathbb{R}^{K},$

nazywa się funkcją regresji. Warunek liniowości można zapisać w postaci macierzowej

$Y=X\beta+\varepsilon,$

gdzie $X$ macierz o wyrazach $X_{{i,k}}$ , $Y$ , $\beta$ i $\varepsilon$ wektory kolumnowe o wyrazach odpowiednio $Y_{i}$ , $\beta _{k}$ i $\varepsilon _{i}$ .

Uwaga 4.5

Założenie Z1 implikuje przynależność $\varepsilon$ do $L^{2}$ .

Z2. Ścisła egzogeniczność.

$E(\epsilon|X)=0.$

Wniosek 4.1

Przy założeniach Z1 i Z2 dla wszystkich $i,j\in\{ 1,\dots,n\}$ i $k\in\{ 1,\dots,K\}$ zachodzą następujące równości:
1. $E(\varepsilon _{i})=0$ ;
2. $E(\varepsilon _{i}X_{{j,k}})=0$ ;
3. $Cov(\varepsilon _{i},X_{{j,k}})=0$ .

Dowód.
Ponieważ zarówno $\varepsilon _{i}$ jak i $X_{{j,k}}$ należą do $L^{2}$ (to wynika z Z1) to możemy stosować twierdzenie o iterowanej wartości oczekiwanej.

Ad1.	$\displaystyle E(\varepsilon _{i})=$	$\displaystyle E(E(\varepsilon _{i}\|X))=E(0)=0.$
Ad2.	$\displaystyle E(\varepsilon _{i}X_{{j,k}})=$	$\displaystyle E(E(\varepsilon _{i}X_{{j,k}}\|X))=E(X_{{j,k}}E(\varepsilon _{i}\|X))=E(0)=0.$
Ad3.	$\displaystyle Cov(\varepsilon _{i},X_{{j,k}})=$	$\displaystyle E(\varepsilon _{i}X_{{j,k}})-E(\varepsilon _{i})E(X_{{j,k}})=0-0=0.$

$\Box$

Z3. Liniowa niezależność.

$(P(rk(X)=K)=1,\mbox{ i }(X^{T}X)^{{-1}}\in L^{1}.$

Warunek Z3 oznacza, że kolumny macierzy $X$ są prawie na pewno liniowo niezależne.

Z4. Sferyczność błędu

$E(\varepsilon\varepsilon^{T}|X)=\sigma^{2}Id_{n},$

gdzie $\sigma>0$ deterministyczny parametr modelu.

Warunek Z4 można rozłożyć na dwa warunki:
Z4.1. Homoskedastyczność

$E(\varepsilon _{i}^{2}|X)=\sigma^{2}.$

Z4.2. Brak korelacji, dla $i\neq j$

$E(\varepsilon _{i}\varepsilon _{j}|X)=0.$

Wniosek 4.2

Przy założeniach Z1, Z2 i Z4 dla wszystkich $i,j\in\{ 1,\dots,n\}$ , $i\neq j$ zachodzą następujące równości:
1. $D^{2}(\varepsilon _{i})=\sigma^{2}$ ;
2. $Cov(\varepsilon _{i},\varepsilon _{j})=0$ .

Z5. Gaussowskość.
Łączny rozkład warunkowy $\varepsilon$ względem $X$ jest normalny.

Wniosek 4.3

Przy założeniach Z1, Z2, Z4 i Z5:
1. $\varepsilon|X\sim N(0,\sigma^{2}Id_{n})$ ;
2. $\varepsilon\sim N(0,\sigma^{2}Id_{n})$ .

Dowód.
Punkt 1 wynika z założeń Z2 i Z5.
Punkt 2 wynika z faktu, że parametry warunkowego rozkładu $\varepsilon$ nie zależy od $X$ . Rzeczywiście, niech $F(e_{1},\dots,e_{n})$ będzie dystrybuantą rozkładu $N(0,\sigma^{2}Id_{n})$ , wówczas

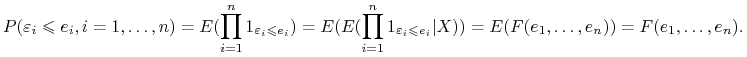$P(\varepsilon _{i}\leq e_{i},i=1,\dots,n)=E(\prod _{{i=1}}^{n}1_{{\varepsilon _{i}\leq e_{i}}})=E(E(\prod _{{i=1}}^{n}1_{{\varepsilon _{i}\leq e_{i}}}|X))=E(F(e_{1},\dots,e_{n}))=F(e_{1},\dots,e_{n}).$

$\Box$

4.4. Estymacja parametrów modelu metodą MNK

Estymatorem MNK wektora $\beta$ jest wektor

$B=(X^{T}X)^{{-1}}X^{T}Y.$

Natomiast estmatorem MNK wariancji $\sigma^{2}$ jest

$S_{Y}^{2}=\frac{\xi^{T}\xi}{n-K}=\frac{SKR_{{min}}}{n-K},$

gdzie $\xi=Y-XB$ .

Twierdzenie 4.1

Własności estymatorów $B$ i $S_{y}$ :
a) nieobciążoność $B$ . Jeśli zachodzą Z1,Z2 i Z3 to

$B\in L^{1}\;\;\;\mbox{ i }\;\;\; E(B|X)=\beta.$

b) skończona wariancja $B$ . Jeśli zachodzą Z1,Z2,Z3 i Z4 to

$Var(B|X)=\sigma^{2}(X^{T}X)^{{-1}}\;\;\;\mbox{ i }\;\;\; B\in L^{2}.$

c) efektywność (tw. Gaussa-Markowa). Jeśli zachodzą Z1,Z2,Z3 i Z4 to estymator MNK jest najefektywniejszy w klasie liniowych po $Y$ , nieobciążonych estymatorów liniowych modeli.

$\forall\beta\;\;\forall\widehat{\beta}\mbox{- lin. nieob. est.}\;\;\;\; Var(\widehat{\beta}|X)-Var(B|X)\geq 0.$

d) nieobciążoność $S_{Y}$ . Jeśli zachodzą Z1,Z2,Z3 i Z4 to

$\xi\in L^{2}\;\;\;\mbox{ i }\;\;\; E(S^{2}_{Y}|X)=\sigma^{2}.$

e) ortogonalność $B$ do składnika resztowego $\xi$ . Jeśli zachodzą Z1,Z2,Z3 i Z4 to

$Cov(B,\xi|X)=0.$

Dowód.
Ad.a. Najpierw pokażemy, że warunki Z3 i Z1 implikują przynależność $B$ do $L^{1}$ . Mamy

$((X^{T}X)^{{-1}}X^{T})((X^{T}X)^{{-1}}X^{T})^{T}=(X^{T}X)^{{-1}}X^{T}X(X^{T}X)^{{-1}}=(X^{T}X)^{{-1}}\in L^{1}.$

Zatem wszystkie wyrazy macierzy $(X^{T}X)^{{-1}}X^{T}$ należą do $L^{2}$ . Ponieważ również $Y\in L^{2}$ , to $B=((X^{T}X)^{{-1}}X^{T})Y$ należy do $L^{1}$ .

Następnie pokażemy, że $E((B-\beta)|X)=0$ .
Mamy dwa równania opisujące zależność $Y$ od $X$ :

	$\displaystyle Y$	$\displaystyle=$	$\displaystyle X\beta+\varepsilon,$
	$\displaystyle Y$	$\displaystyle=$	$\displaystyle XB+\xi.$

Po odjęciu stronami otrzymujemy:

$X(B-\beta)=\varepsilon-\xi.$

(4.1)

Mnożymy obie strony przez $(X^{T}X)^{{-1}}X^{T}$

$(X^{T}X)^{{-1}}X^{T}X(B-\beta)=(X^{T}X)^{{-1}}X^{T}\varepsilon-(X^{T}X)^{{-1}}X^{T}\xi.$

Biorąc pod uwagę, że $X^{T}\xi=0$ (patrz wniosek 2.1) otrzymujemy:

$B-\beta=(X^{T}X)^{{-1}}X^{T}\varepsilon.$

(4.2)

Zatem

$E((B-\beta)|X)=E((X^{T}X)^{{-1}}X^{T}\varepsilon|X)=(X^{T}X)^{{-1}}X^{T}E(\varepsilon|X)=0.$

Ad.b. Pokażemy, że dla każdego wektora kolumnowego $v\in\mathbb{R}^{K}\;\;$ $D^{2}(v^{T}B|X)=\sigma^{2}v^{T}(X^{T}X)^{{-1}}v$ . Skorzystamy z faktu, że wartości oczekiwane nieujemnych zmiennych losowych są zawsze określone.

$\displaystyle D^{2}(v^{T}B\|X)$	$\displaystyle=$	$\displaystyle D^{2}(v^{T}(B-\beta)\|X)=D^{2}(v^{T}(X^{T}X)^{{-1}}X^{T}\varepsilon\|X)=$
	$\displaystyle=$	$\displaystyle E(v^{T}(X^{T}X)^{{-1}}X^{T}\varepsilon\varepsilon^{T}X(X^{T}X)^{{-1}}v\|X)=$
	$\displaystyle=$	$\displaystyle v^{T}(X^{T}X)^{{-1}}X^{T}E(\varepsilon\varepsilon^{T}\|X)X(X^{T}X)^{{-1}}v=$
	$\displaystyle=$	$\displaystyle v^{T}(X^{T}X)^{{-1}}X^{T}(\sigma^{2}Id_{n})X(X^{T}X)^{{-1}}v=$
	$\displaystyle=$	$\displaystyle\sigma^{2}v^{T}(X^{T}X)^{{-1}}X^{T}X(X^{T}X)^{{-1}}v=$
	$\displaystyle=$	$\displaystyle\sigma^{2}v^{T}(X^{T}X)^{{-1}}v.$

Założenie, że $(X^{T}X)^{{-1}}\in L^{1}$ (Z3) implikuje skończoność wariancji $v^{T}B$ dla każdego $v$ , a więc i wariancji $B$ .

	$\displaystyle D^{2}(v^{T}B)$	$\displaystyle=$	$\displaystyle D^{2}(v^{T}(B-\beta))=E(v^{T}(B-\beta)(B-\beta)^{T}v)=$
		$\displaystyle=$	$\displaystyle E(E(v^{T}(B-\beta)(B-\beta)^{T}v\|X))=\sigma^{2}v^{T}E(X^{T}X)^{{-1}})v<+\infty.$

Ad.c. Niech $\widehat{\beta}$ będzie dowolnym nieobciążonym i liniowym po $Y$ estymatorem dla modeli liniowych z $K$ parametrami strukturalnymi i $n$ obserwacjami. Wówczas istnieje funkcja macierzowa $C(\cdot)$ ( $C\in K\times n$ ), taka, że

$\widehat{\beta}=C(X)Y.$

Niech $G=C-(X^{T}X)^{{-1}}X^{T}$ .

$\widehat{\beta}=(G+(X^{T}X)^{{-1}}X^{T})Y=GY+(X^{T}X)^{{-1}}X^{T}Y=G(X\beta+\varepsilon)+B.$

Ponieważ oba estymatory $B$ i $\widehat{\beta}$ są nieobciążone to

$\beta=E(\widehat{\beta}|X)=GX\beta+GE(\varepsilon|X)+E(B|X)=GX\beta+0+\beta.$

Czyli dla dowolnego wektora $\beta\;\;$ $GX\beta=0$ , a zatem $GX=0$ . W efekcie otrzymujemy:

$\widehat{\beta}=G\varepsilon+B,$

$\widehat{\beta}-\beta=G\varepsilon+B-\beta=(G+(X^{T}X)^{{-1}}X^{T})\varepsilon.$

Teraz możemy wyznaczyc warunkową wariancje $\widehat{\beta}$ .

$\displaystyle Var(\widehat{\beta}\|X)$	$\displaystyle=$	$\displaystyle Var(\widehat{\beta}-\beta)=Var((G+(X^{T}X)^{{-1}}X^{T})\varepsilon\|X)=$
	$\displaystyle=$	$\displaystyle E((G+(X^{T}X)^{{-1}}X^{T})\varepsilon\varepsilon^{T}(G^{T}+X(X^{T}X)^{{-1}})\|X)=$
	$\displaystyle=$	$\displaystyle(G+(X^{T}X)^{{-1}}X^{T})E(\varepsilon\varepsilon^{T}\|X)(G^{T}+X(X^{T}X)^{{-1}})=$
	$\displaystyle=$	$\displaystyle(G+(X^{T}X)^{{-1}}X^{T})(\sigma^{2}Id_{n})(G^{T}+X(X^{T}X)^{{-1}})=$
	$\displaystyle=$	$\displaystyle\sigma^{2}(GG^{T}+GX(X^{T}X)^{{-1}}+(X^{T}X)^{{-1}}X^{T}G^{T}+(X^{T}X)^{{-1}}).$

Ponieważ $GX=0$ a $Var(B|X)=\sigma^{2}(X^{T}X)^{{-1}}$ , to

$Var(\widehat{\beta}|X)-Var(B|X)=\sigma^{2}GG^{T}\geq 0.$

Ad.d. Z równań 4.1 i 4.2 otrzymujemy, że

$\xi=\varepsilon-X(B-\beta)=(Id-X(X^{T}X)^{{-1}}X^{T})\varepsilon=M\varepsilon.$

Jak pokazaliśmy w lemacie 2.2 macierz $M$ jest symetryczna i idempotentna, zatem

$\xi^{T}\xi=\varepsilon^{T}MM\varepsilon=\varepsilon^{T}M\varepsilon.$

(4.3)

Ponieważ, $\xi^{T}\xi$ to suma kwadratów $\xi _{t}$ to jej wartości oczekiwane są zawsze określone. Otrzymujemy na mocy warunku Z3 i lematu 2.2

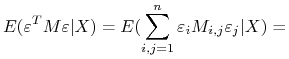	$\displaystyle E(\xi^{T}\xi\|X)$	$\displaystyle=$	$\displaystyle E(\varepsilon^{T}M\varepsilon\|X)=E(\sum _{{i,j=1}}^{n}\varepsilon _{i}M_{{i,j}}\varepsilon _{j}\|X)=$
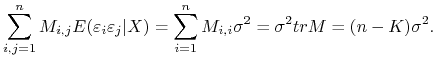		$\displaystyle=$	$\displaystyle\sum _{{i,j=1}}^{n}M_{{i,j}}E(\varepsilon _{i}\varepsilon _{j}\|X)=\sum _{{i=1}}^{n}M_{{i,i}}\sigma^{2}=\sigma^{2}trM=(n-K)\sigma^{2}.$

Ponadto

$E(\xi^{T}\xi)=E(E(\xi^{T}\xi|X))=(n-K)\sigma^{2}.$

Zatem $\xi$ należy do $L^{2}$ .

Ad.e. Biorąc pod uwagę, że $\xi=\varepsilon-X(B-\beta)$ (równanie 4.1) i $E(\xi|X)=0$ to

$\displaystyle Cov(B,\xi\|X)$	$\displaystyle=$	$\displaystyle E((B-\beta)(\varepsilon-X(B-\beta))^{T}\|X)=$
	$\displaystyle=$	$\displaystyle E(-(B-\beta)(B-\beta)^{T}X^{T}+(B-\beta)\varepsilon^{T}\|X)=$
	$\displaystyle=$	$\displaystyle-Var(B-\beta\|X)X^{T}+E((X^{T}X)^{{-1}}X^{T}\varepsilon\varepsilon^{T}\|X)=$
	$\displaystyle=$	$\displaystyle-\sigma^{2}(X^{T}X)^{{-1}}X^{T}+(X^{T}X)^{{-1}}X^{T}E(\varepsilon\varepsilon^{T}\|X)=$
	$\displaystyle=$	$\displaystyle-\sigma^{2}(X^{T}X)^{{-1}}X^{T}+(X^{T}X)^{{-1}}X^{T}(\sigma^{2}Id_{n})=0.$

$\Box$

Wniosek 4.4

”Bezwarunkowe” własności estymatora MNK $B$ .
a. Warunki Z1,Z2 i Z4 implikują, że $E(B)=\beta$ .
b. Warunki Z1,Z2,Z3 i Z4 implikują, że $Cov(B,\xi)=0$ .

Dowód.

$E(B)=E(E(B|X))=E(\beta)=\beta.$

$Cov(B,\xi)=Cov(B-\beta,\xi)=E((B-\beta)\xi^{T})=E(E((B-\beta)\xi^{T}|X))=E(Cov(B,\xi|X))=0.$

$\Box$

Wniosek 4.5

Estymacja warunkowej kowariancji estymatora $B$ .
1. $S^{2}_{Y}(X^{T}X)^{{-1}}$ jest naturalnym nieobciążonym estymatorem $Var(B|X)$ .
2. $S^{2}_{Y}(X^{T}X)^{{-1}}_{{k,k}}$ jest naturalnym nieobciążonym estymatorem $D^{2}(b_{k}|X)$ .

Dowód.
Pokażemy, że dla każdego wektora kolumnowego $v\in\mathbb{R}^{K}\;\;$ $E(S^{2}_{Y}v^{T}(X^{T}X)^{{-1}}v|X)=\sigma^{2}v^{T}(X^{T}X)^{{-1}}v$ . Skorzystamy z faktu, że wartości oczekiwane nieujemnych zmiennych losowych są zawsze określone.

$E(S^{2}_{Y}v^{T}(X^{T}X)^{{-1}}v|X)=E(S^{2}_{Y}|X)v^{T}(X^{T}X)^{{-1}}v=\sigma^{2}v^{T}(X^{T}X)^{{-1}}v=Var(v^{T}B|X).$

$\Box$

Oznaczenie.

$SE(b_{k})=\sqrt{S^{2}_{Y}(X^{T}X)^{{-1}}}.$

Uwaga 4.6

Związek wariancji estymatora $B$ z wielkością próby.
Załóżmy, że poszczególne wiersze macierzy $X$ (czyli obserwacje) są niezależne od siebie i o tym samym rozkładzie co pewien horyzontalny wektor losowy $Z$ . Wówczas z prawa wielkich liczb otrzymujemy, że istnieje pewna macierz $C$ taka, że

$\lim _{{n\rightarrow\infty}}\frac{1}{n}X^{T}X=C=E(ZZ^{T}).$

Warunek Z3 implikuje, że macierz $C$ jest odwracalna. Zatem

$\lim _{{n\rightarrow\infty}}n(X^{T}X)^{{-1}}=C^{{-1}}.$

W efekcie

$\lim _{{n\rightarrow\infty}}Var(B|X)=\lim _{{n\rightarrow\infty}}\frac{\sigma^{2}}{n}(n(X^{T}X)^{{-1}})=0.$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

	$\displaystyle E(\xi^{T}\xi\|X)$	$\displaystyle=$	$\displaystyle E(\varepsilon^{T}M\varepsilon\|X)=E(\sum _{{i,j=1}}^{n}\varepsilon _{i}M_{{i,j}}\varepsilon _{j}\|X)=$
		$\displaystyle=$	$\displaystyle\sum _{{i,j=1}}^{n}M_{{i,j}}E(\varepsilon _{i}\varepsilon _{j}\|X)=\sum _{{i=1}}^{n}M_{{i,i}}\sigma^{2}=\sigma^{2}trM=(n-K)\sigma^{2}.$

Ekonometria

Zagadnienia

4. Klasyczny model regresji

4.1. Notacja macierzowa dla zmiennych losowych

Definicja 4.1

Uwaga 4.1

Definicja 4.2

Uwaga 4.2

Definicja 4.3

Uwaga 4.3

4.2. Warunkowa wartość oczekiwana

Definicja 4.4

Lemat 4.1

Uwaga 4.4

4.3. Założenia klasycznego modelu regresji

Uwaga 4.5

Wniosek 4.1

Wniosek 4.2

Wniosek 4.3

4.4. Estymacja parametrów modelu metodą MNK

Twierdzenie 4.1

Wniosek 4.4

Wniosek 4.5

Uwaga 4.6