Zagadnienia
9. Teoria dużej próbki
Teoria dużej próbki. Założenia modelu. Asymptotyczne własności estymatorów MNK. Statystyczna weryfikacja modelu. (2 wykłady)
9.1. Założenia modelu
W teorii dużej próbki przez model rozumie się ![]() wymiarowy proces stochastyczny
wymiarowy proces stochastyczny
spełniający pewne założenia.
Z̃1. Liniowość.
Z̃2. Stacjonarność i ergodyczność.![]() wymiarowy proces stochastyczny
wymiarowy proces stochastyczny
![]() jest stacjonarny i ergodyczny.
jest stacjonarny i ergodyczny.
Uwaga.
Z warunków Z̃1 i Z̃2 wynika, że również proces ![]() jest stacjonarny i ergodyczny.
jest stacjonarny i ergodyczny.
Z̃3. Warunek maksymalnego rzędu.
Proces ![]() jest klasy
jest klasy ![]() i
i ![]() macierz
macierz
jest odwracalna.
Uwaga.
Ze stacjonarności procesu ![]() wynika, że macierz
wynika, że macierz ![]() nie zależy od
nie zależy od ![]() .
.
Z̃4. Ortogonalność zmiennych objaśniających do składnika losowego.
Oznaczenie.
Uwaga.
Z warunków Z̃1 i Z̃2 wynika, że również proces ![]() jest stacjonarny i ergodyczny.
jest stacjonarny i ergodyczny.
Z̃5. Martyngałowość.
Proces ![]() jest ciągiem przyrostów martyngałowych,
jest ciągiem przyrostów martyngałowych,
![]() jest klasy
jest klasy ![]() i
i ![]() macierz
macierz
jest odwracalna.
Uwaga.
1. Ze stacjonarności procesu ![]() wynika, że macierz
wynika, że macierz ![]() nie zależy od
nie zależy od ![]() .
.
2. Z centralnego twierdzenia granicznego (8.6) wynika , że ![]() jest równa
asymptotycznej wariancji procesu średnich
jest równa
asymptotycznej wariancji procesu średnich ![]()
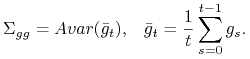 |
Z̃6. Warunkowa homoskedastyczność.
Lemat 9.1
Z warunków Z̃2 i Z̃6 wynika, że
Dowód.![]() , zatem
, zatem
Uwaga 9.1
Aksjomaty Z̃ modelu dużej próbki (poza Z̃2) są słabsze od aksjomatów Z modelu klasycznego.
Otóż, niech ![]() będzie
będzie ![]() wymiarowym, klasy
wymiarowym, klasy ![]() , stacjonarnym i ergodycznym
procesem stochastycznym, wówczas
jeśli dla każdego
, stacjonarnym i ergodycznym
procesem stochastycznym, wówczas
jeśli dla każdego ![]() jego początkowy fragment
jego początkowy fragment ![]() spełnia aksjomaty
Z1, Z2, Z3, Z4 i Z5 to
spełnia on
Z̃1, Z̃2, Z̃3, Z̃4, Z̃5 i Z̃6.
spełnia aksjomaty
Z1, Z2, Z3, Z4 i Z5 to
spełnia on
Z̃1, Z̃2, Z̃3, Z̃4, Z̃5 i Z̃6.
9.2. Asymptotyka estymatorów MNK
Niech ![]() będzie procesem generującym dane.
W modelu dużej próbki, podobnie jak w modelu klasycznym, będziemy estymowali parametry modelu
będzie procesem generującym dane.
W modelu dużej próbki, podobnie jak w modelu klasycznym, będziemy estymowali parametry modelu ![]() i
i ![]() w oparciu o metodę najmniejszym kwadratów. Niech
w oparciu o metodę najmniejszym kwadratów. Niech ![]() oznacza ilość obserwacji (
oznacza ilość obserwacji (![]() ),
), ![]() macierz wymiaru
macierz wymiaru ![]() , której wierszami są wektory losowe
, której wierszami są wektory losowe ![]() a
a ![]() wektor kolumnowy wymiaru
wektor kolumnowy wymiaru ![]() o wyrazach
o wyrazach ![]() . Estymatory MNK możemy zapisać na dwa sposoby jako iloczyn macierzy
. Estymatory MNK możemy zapisać na dwa sposoby jako iloczyn macierzy ![]() i
i ![]() lub za pomocą średnich z iloczynów
lub za pomocą średnich z iloczynów ![]() i
i ![]() .
.
Gdy macierz ![]() ma rząd maksymalny czyli
ma rząd maksymalny czyli ![]() , to estymator MNK wektora
, to estymator MNK wektora ![]() wynosi
wynosi
gdzie
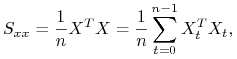 |
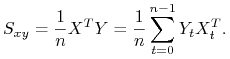 |
W wyjątkowych przypadkach gdy rząd macierzy ![]() jest mniejszy niż
jest mniejszy niż ![]() to jako
to jako ![]() bierzemy dowolny wektor minimalizujący sumę kwadratów reszt – patrz uwaga 2.1.
bierzemy dowolny wektor minimalizujący sumę kwadratów reszt – patrz uwaga 2.1.
Natomiast estymator MNK parametru ![]() wynosi
wynosi
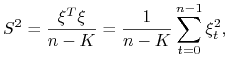 |
gdzie
Omówimy teraz podstawowe własności powyższych estymatorów w zależności od wielkości próbki ![]() .
.
Twierdzenie 9.1
Własności estymatorów ![]() i
i ![]() :
:
a. Zgodność ![]()
b. Asymptotyczna normalność ![]()
gdzie
Jeśli dodatkowo założymy Z̃6, to
c. Zgodność ![]()
Jeśli dodatkowo założymy Z̃6, to
d. Zgodna estymacja ![]()
Dowód.
Mamy dwa równania opisujące zależność ![]() od
od ![]() :
:
Po odjęciu stronami otrzymujemy:
| (9.1) |
Mnożymy obie strony przez ![]()
Następnie liczymy średnią po ![]() .
Biorąc pod uwagę, że
.
Biorąc pod uwagę, że ![]() (patrz wniosek 2.1) otrzymujemy:
(patrz wniosek 2.1) otrzymujemy:
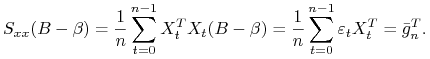 |
Ponieważ proces ![]() jest stacjonarny i ergodyczny to
jest stacjonarny i ergodyczny to
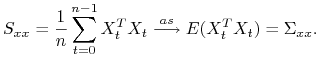 |
Macierz ![]() jest odwracalna (warunek Z̃3), zatem dla dużych
jest odwracalna (warunek Z̃3), zatem dla dużych ![]() również macierz
również macierz ![]() jest odwracalna.
W wyjątkowych przypadkach gdy
jest odwracalna.
W wyjątkowych przypadkach gdy ![]() dookreślamy
dookreślamy ![]() w dowolny sposób.
w dowolny sposób.
Po przemnożeniu obu stron przez macierz ![]() otrzymujemy równość analogiczną do 4.2
otrzymujemy równość analogiczną do 4.2
| (9.2) |
gdzie ![]() dla
dla ![]() odpowiednio dużych.
odpowiednio dużych.
Ad. a.
Ponieważ proces ![]() jest stacjonarny i ergodyczny to z warunku Z̃4 otrzymujemy
jest stacjonarny i ergodyczny to z warunku Z̃4 otrzymujemy
Zatem
Ad. b.
Proces ![]() oprócz tego, że jest stacjonarny i ergodyczny to jest ciągiem przyrostów martyngałowych,
a więc ((8.6))
oprócz tego, że jest stacjonarny i ergodyczny to jest ciągiem przyrostów martyngałowych,
a więc ((8.6))
Zatem
Jeśli ponadto założymy Z̃6 to
zatem
Ad. c.
Przepisując odpowiednio równanie 9.1 otrzymujemy
Zatem
Po uśrednieniu otrzymujemy
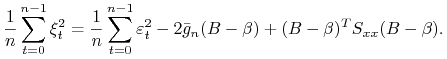 |
Przechodzimy do granicy. Ponieważ
to otrzymujemy, że
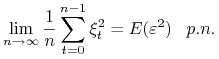 |
Zatem
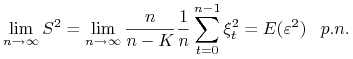 |
Jeśli ponadto założymy Z̃6 to
zatem
Ad. d.
Korzystając z warunku Z̃6 otrzymujemy




