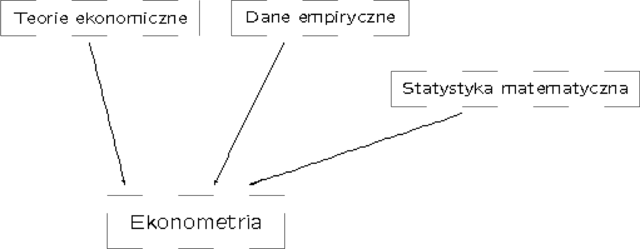
W skrócie można powiedzieć, że ekonometria to zestawienie danych empirycznych z teoriami ekonomicznymi przy zastosowaniu statystyki matematycznej.

Podstawowe cele ekonometrii to:
1. Analiza danych empirycznych i prognozowanie na ich podstawie;
2. Weryfikacja i kalibrowanie teorii ekonomicznych.

Kluczowym obiektem w ekonometrii jest tzw. model ekonometryczny. Zapisujemy go w postaci

gdzie zwykle oznacza czas – kolejny moment lub kolejny przedział czasowy (dzień, miesiąc, rok …), ale może też oznaczać numer porządkowy obserwacji (np. firmy, której dotyczą dane czy województwa).
to wektor zmiennych objaśniających,
to wektor zmiennych objaśnianych,
nazywa się postacią analityczną modelu, jest to funkcja o wartościach w ;
a nazywa się składnikiem losowym.

Przedstawimy teraz uproszczony schemat konstrukcji modelu ekonometrycznego. Możemy wyróżnić trzy operacje: Zbieramy dane historyczne (empiryczne) , .

Konstruujemy model , gdzie - błąd przybliżenia.

Konstruujemy model stochastyczny , gdzie i to zmienne losowe, których realizacją są nasze obserwacje i , a to składnik losowy (też zmienne losowe).

Zakładamy, że w przyszłości i będą związane tą samą zależnością jak dotychczas.

Proszę zwrócić uwagę, że dwie pierwsze operacje aproksymację i estymację możemy wykonać dowolnie dokładnie. Natomiast o ekstrapolacji zawsze ”matematyk teoretyk” będzie mógł powiedzieć, że to ”wróżenie z fusów”.

1. Model konsumpcji
Przez oznaczamy całkowity popyt konsumpcyjny w miesiącu , a przez dochody gospodarstw domowych w tym okresie. Przyjmujemy, że

gdzie wydatki stałe, część dochodów przeznaczona na konsumpcję, a składnik losowy.
Zauważmy, że składnik losowy ”zawiera w sobie” wszystkie czynniki nie uwzględnione w sposób jawny w modelu.

Uwagi:
W modelu zakładamy, że i są stałe, a w rzeczywistości są one tylko wolno-zmienne. Istotną wadą powyższego modelu jest nieuwzględnienie oszczędności.

2. Model oszczędności
Przez oznaczamy stan oszczędności na koniec miesiąca , a przez dochody gospodarstw domowych w tym miesiącu. Przyjmujemy, że

gdzie wydatki stałe, część dochodów przeznaczona na oszczędności, część oszczędności przeznaczona na konsumpcję, a składnik losowy.

Uwagi:
Zauważmy, że w powyższym modelu opóźniona zmienna objaśniana jest zmienną objaśniająca.

Model 1 i 2 można połączyć i otrzymać model dwurównaniowy.

3. Model konsumpcji z uwzględnieniem oszczędności
Przez oznaczamy całkowity popyt konsumpcyjny w miesiącu , przez oznaczamy stan oszczędności, a przez dochody gospodarstw domowych w tym okresie. Przyjmujemy, że

gdzie

Uwagi:
Na powyższym przykładzie widzimy, jak z prostszych modeli można konstruować bardziej skomplikowane.
Pytanie: Czy w ten sposób uzyskujemy lepszy opis badanego zjawiska?
Okazuje się, że nie zawsze. Wyznaczanie wartości parametrów dla bardziej złożonego modelu, jest zwykle bardziej skomplikowane i mniej dokładne. W efekcie złożony model, który jest teoretycznie lepszy, w praktyce już takim być nie musi.

4. Model popytu dla dóbr konsumpcyjnych
Przez oznaczamy popyt dla wybranego dobra konsumpcyjnego, przez jego cenę, a przez dochody nabywcy. Przyjmujemy, że

Uwagi:
Jest to przykład modelu nieliniowego, który można zlinearyzować za pomocą logarytmowania.

5. Model stochastyczny kursu walutowego
Niech oznacza kurs 1 USD w EUR w dniu . Przyjmujemy

Po zlogarytmowaniu otrzymujemy model błądzenia przypadkowego

6. Model wydajności pracy
Niech oznacza wydajność pracy w PLN na 1 pracownika, a techniczne uzbrojenie miejsca pracy też w PLN na 1 pracownika. Przyjmujemy

Po zlogarytmowaniu otrzymujemy

Uwagi:
Współczynnik mierzy skalę postępu techniczno-organizacyjnego.

1. Klasyfikacja ze względu na dynamikę:
a. Modele statyczne (jednokresowe) charakteryzujące się brakiem zależności od czasu, tzn. nie zależy od czasu i wśród zmiennych objaśniających nie ma opóźnionych zmiennych objaśnianych. Przykłady 1 i 4.
b. Modele dynamiczne – zależne od czasu lub od opóźnionych zmiennych objaśnianych. Przykłady 2, 3, 5 i 6.
W klasie modeli dynamicznych wyróżniamy modele autoregresyjne w których zależność od czasu wiąże się tylko z występowaniem zmiennych opóźnionych. Przykłady 2, 3 i 5.

2. Klasyfikacja ze względu na postać analityczną modelu:
a. Modele liniowe, postać analityczna jest zadana przez funkcję liniową. Przykłady 1, 2 i 3.
b. Modele nieliniowe, postać analityczna nie jest zadana przez funkcję liniową.
W klasie modeli nieliniowych wyróżniamy modele multiplikatywne, które można zlinearyzować poprzez zlogarytmowanie. Przykłady 4, 5 i 6.

2. Klasyfikacja ze względu na wymiar zmiennej objaśnianej:
a. Modele jednorównaniowe. Przykłady 1, 2, 4, 5 i 6.
b. Modele wielorównaniowe. Przykład 3.

Klasyfikacja ze względu na dynamikę wiąże się z planowanym wykorzystaniem modelu. Do prognozowania potrzebne są modele dynamiczne. Natomiast do badania wpływu zmian konkretnych czynników wystarczy model statyczny.

Klasyfikacja ze względu na postać analityczną modelu i wymiar określa złożoność kalibracji modelu. Jeśli model jest liniowy i jednorównaniowy to istnieją ogólne, w miarę proste, algorytmy (które omówimy na dalszych wykładach) pozwalające sprawnie wyestymować parametry modelu. W przeciwnym wypadku algorytm zależy od konkretnego przypadku i zwykle jest dużo bardziej skomplikowany.