Zagadnienia

12.1 Przykład E.Fama - konstrukcja modelu
12.2 Hipoteza efektywnego rynku
12.3 Analiza danych empirycznych

12. Hipoteza efektywnego rynku - ekonometria racjonalnych oczekiwań

Teoria dużej próbki cd. Przykład: Teoria racjonalnych oczekiwań. (1 wykład)

12.1. Przykład E.Fama - konstrukcja modelu

Określenie.
Mówimy, że rynek jest efektywny, gdy w sposób efektywny wykorzytywana jest posiadana informacja. Ceny na efektywnym rynku ”w pełni” odzwierciedlają dostępne informacje.

Przeanalizujemy przykład E.Fama, aby sprawdzić na ile rynek amerykańskich bonów skarbowych jest efektywny. Ograniczymy się do bonów jednomiesięcznych.

Charakterystyka instrumentu:
$\bullet$ czas życia 1 miesiąc,
$\bullet$ wypłata 100 USD,
$\bullet$ zakup z dyskontem.

Podstawą analizy będą dane miesięczne:
$t$ – numer kolejny miesiąca;
$V_{t}$ – cena bonu na początku miesiąca $t$ ;
$P_{t}$ – indeks cen konsumenta (CPI) na początku miesiąca $t$ (por. [10], §1.4).

Na ich podstawie wyznaczamy:
$R_{t}$ – miesięczną stopę zwrotu dla bonów w miesiącu $t$

$R_{t}=\frac{1-V_{t}}{V_{t}},\;\;\;\mbox{ czyli }\;\;\; V_{t}=\frac{1}{1+R_{t}};$

$\pi _{t}$ – miesięczną stopę inflacji od początku miesiąca $t-1$ do początku miesiąca $t$

$\pi _{t}=\frac{P_{t}-P_{{t-1}}}{P_{{t-1}}}=\frac{P_{t}}{P_{{t-1}}}-1;$

$r_{t}$ – realną stopę zwrotu w miesiącu $t-1$ (por.[10], §1.4)

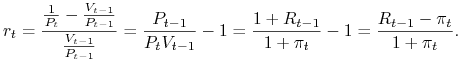$r_{t}=\frac{\frac{1}{P_{t}}-\frac{V_{{t-1}}}{P_{{t-1}}}}{\frac{V_{{t-1}}}{P_{{t-1}}}}=\frac{P_{{t-1}}}{P_{t}V_{{t-1}}}-1=\frac{1+R_{{t-1}}}{1+\pi _{t}}-1=\frac{R_{{t-1}}-\pi _{t}}{1+\pi _{t}}.$

Ze względu na małą inflację będziemy stosowali wzór przybliżony

$r_{t}\approx R_{{t-1}}-\pi _{t}.$

Ponadto w analizie uwzględnimy wielkości nieobserwowalne:
$\widehat{\pi}_{{t+1,t}}$ – prognozowaną (oczekiwaną) na początku miesiąca $t$ stopę inflacji w miesiącu $t$ ( $\widehat{\pi}_{{t+1,t}}$ jest prognozą $\pi _{{t+1}}$ );
$\eta _{t}$ – błąd prognozy inflacji

$\eta _{t}=\pi _{t}-\widehat{\pi}_{{t,t-1}};$

$\widehat{r}_{{t+1,t}}$ – prognozowaną (oczekiwaną) na początku miesiąca $t$ realną stopę zwrotu z bonów w miesiącu $t$ ( $\widehat{r}_{{t+1,t}}$ jest prognozą $r_{{t+1}}$ );

$\widehat{r}_{{t+1,t}}=\frac{R_{t}-\widehat{\pi}_{{t+1,t}}}{1+\widehat{\pi}_{{t+1,t}}}\approx R_{t}-\widehat{\pi}_{{t+1,t}};$

${\cal I}_{t}$ – zasób informacji dostępny dla inwestorów na początku miesiąca $t$

	a)		$\displaystyle{\cal I}_{t}\supset\{ R_{t},R_{{t-1}},\dots,\pi _{t},\pi _{{t-1}},\dots\},$
	b)		$\displaystyle{\cal I}_{{t}}\supseteq{\cal I}_{{t-1}}\supseteq{\cal I}_{{t-2}}\supseteq\dots.$

Własność b) oznacza, że agenci nie zapominają informacji z poprzednich miesięcy.

${\cal I}_{t}$ modelujemy jako $\sigma$ -ciała, natomiast $V_{t},P_{t},R_{t},\pi _{t},r_{t},\widehat{\pi}_{{t+1,t}},\eta _{t},\widehat{r}_{{t+1,t}}$ modelujemy jako zmienne losowe klasy $L^{2}$ mierzalne względem ${\cal I}_{t}$ .

12.2. Hipoteza efektywnego rynku

Hipoteza efektywnego rynku opiera się na dwóch założeniach:
E1. Racjonalne oczekiwania inflacyjne

$\widehat{\pi}_{{t+1,t}}=E(\pi _{{t+1}}|{\cal I}_{t}).$

E2. Stała oczekiwana realna stopa zwrotu

$\exists r\;\;\;\forall t\;\;\;\widehat{r}_{{t+1,t}}=r.$

Przeanalizujemy wnioski jakie wynikają z założeń E1 i E2.

Lemat 12.1

	a)		$\displaystyle E(\eta _{{t+1}}\|{\cal I}_{{t}})=0;$
	b)		$\displaystyle{\cal I}_{{t}}\supseteq\sigma\{\eta _{t},\eta _{{t-1}},\dots\};$
	c)		$\displaystyle\mbox{proces }\{\eta _{t}\}\mbox{ jest ciągiem przyrostów martyngałowych.}$

Dowód.
Ad a.

$E(\eta _{{t+1}}|{\cal I}_{{t}})=E(\pi _{{t+1}}-\widehat{\pi}_{{t+1,t}}|{\cal I}_{{t}})=E(\pi _{{t+1}}|{\cal I}_{{t}})-\widehat{\pi}_{{t+1,t}}=\widehat{\pi}_{{t+1,t}}-\widehat{\pi}_{{t+1,t}}=0.$

Punkt b wynika z faktu, że dla $s\leq t$ zmienna losowa $\eta _{s}$ jest ${\cal I}_{{s}}$ mierzalna zatem

$\sigma(\eta _{s})\subset{\cal I}_{{s}}\subset{\cal I}_{{t}}.$

Punkt c wynika z a i b.

$E(\eta _{{t+1}})=E(E(\eta _{{t+1}}|{\cal I}_{{t}}))=E(0)=0.$

$E(\eta _{{t+1}}|\eta _{t},\eta _{{t-1}},\dots)=E(E(\eta _{{t+1}}|{\cal I}_{{t}})|\eta _{t},\eta _{{t-1}},\dots)=E(0|\dots)=0.$

$\Box$

Szczególnie ważne są wnioski dotyczące wielkości obserwowalnych gdyż można je przetestować.

Wniosek 12.1

	a)		$\displaystyle R_{{t-1}}-\pi _{t}=r-\eta _{t};$
	b)		$\displaystyle E(r_{{t}})=r;$
	c)		$\displaystyle\mbox{proces }\{ r_{t}\}\mbox{ nie jest autoskorelowany;}$
	d)		$\displaystyle E(\pi _{{t+1}}\|{\cal I}_{{t}})=-r+R_{t}.$

Dowód.
Zauważmy, że z przyjętych założeń wynika co następuje

$R_{{t-1}}-\pi _{t}=(R_{{t-1}}-\widehat{\pi}_{{t,t-1}})-(\pi _{t}-\widehat{\pi}_{{t,t-1}})=\widehat{r}_{{t,t-1}}-\eta _{t}=r-\eta _{t}.$

Z drugiej strony

$R_{{t-1}}-\pi _{t}=r_{t},$

zatem

$r_{t}=r-\eta _{t}.$

Ponieważ stopa $r$ jest deterministyczna to

$E(r_{t})=r-E(\eta _{t})=r.$

Ponadto proces $\{\eta _{t}\}$ jest ciągiem przyrostów martyngałowych, zatem nie jest on autoskorelowany i to samo dotyczy procesu $\{ r_{t}\}$ . Punkt d wynika z faktu, że

$\pi _{{t+1}}=R_{t}-r+\eta _{{t+1}}.$

Zatem

$E(\pi _{{t+1}}|{\cal I}_{{t}})=E(R_{t}-r+\eta _{{t+1}}|{\cal I}_{{t}})=R_{t}-r+E(\eta _{{t+1}}|{\cal I}_{{t}})=R_{t}-r.$

$\Box$

12.3. Analiza danych empirycznych

Fam poddał analizie dane z okresu styczeń 1953 – lipiec 1971 obejmującego 223 miesiące.

12.3.1. Test na autokorelację realnych stóp zwrotu

W oparciu o próbę z 223 miesięcy wyznaczamy współczynniki autokorelacji szeregu czasowego $r_{t}$ , a następnie statystyki $Q$ Ljunga-Boxa dla $j=1,2,\dots,12$ współczynników autokorelacji. Wyniki przedstawione są w tabeli 12.1. W ostatniej kolumnie są przedstawione ”asymptotyczne” $p$ -wartości ( $p$ -value) wyznaczone według wzoru

$p_{j}=1-\chi^{2}_{j}(Q_{j})$

gdzie $\chi^{2}_{j}$ dystrybuanta rozkładu chi kwadrat z $j$ stopniami swobody (granicznego rozkładu $Q_{j}$ gdy wielkość próbki rośnie do nieskończoności).

$j$	$\widehat{\rho}_{p}$	$Q$	$p$ -value
1	-0,101	2,3	0,128
2	0,172	9,1	0,011
3	-0,019	9,1	0,027
4	-0,004	9,1	0,058
5	-0,064	10,1	0,073
6	-0,021	10,2	0,117
7	-0,091	12,1	0,096
8	0,094	14,2	0,076
9	0,094	16,3	0,061
10	0,019	16,4	0,089
11	0,004	16,4	0,128
12	0,207	26,5	0,009

Tabela 12.1. Współczynniki autokorelacji i statystyki $Q$ Ljunga-Boxa

Otrzymane $p$ -wartości $p_{j}$ należą do przedziału $(0{,}9\%,12{,}8\%)$ co można uznać za potwierdzenie hipotezy o braku autokorelacji.

12.3.2. Test predykcji stopy inflacji 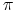$\pi$ w oparciu o nominalną stopę zwrotu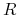 $R$

Z założeń modelu wynika, że stopa inflacji $\pi _{{t+1}}$ i nominalna stopa zwrotu $R_{t}$ są związane zależnością liniową

$\pi _{{t+1}}=R_{t}-r+\eta _{{t+1}},$

gdzie $r$ jest stałą, a $\eta$ można interpretować jako składnik losowy.

Aby zweryfikować powyższą równość wyznaczymy parametry strukturalne modelu regresji z wyrazem wolnym

$\pi _{{t+1}}=\beta _{1}R_{t}+\beta _{2}+\eta _{{t+1}},$

(12.1)

a następnie przetestujemy prawdziwość hipotezy

$H_{0}:\beta _{1}=1\;\;\;\mbox{ wobec }\;\;\; H_{1}:\beta _{1}\neq 1.$

Sprawdzamy czy dla modelu opisanego równaniem 12.1 spełnione są założenia modelu dużej próbki Z̃1-Z̃6.

Warunek Z̃1.
Kładziemy $Y_{t}=\pi _{{t+1}}$ , $X_{t}=(R_{t},1)$ i $\varepsilon _{t}=\eta _{{t+1}}$ , otrzymujemy

$Y_{t}=X_{t}\beta+\varepsilon _{t}.$

Warunek Z̃2.
Stacjonarność i ergodyczność procesu $\{(Y_{t},X_{t})\}$ przyjmujemy (,,na wiarę”) po analizie wykresu.

Warunek Z̃3.

$X_{t}^{T}X_{t}=\left(\begin{array}[]{c}R_{t}\\ 1\end{array}\right)\cdot(R_{t},1)=\left(\begin{array}[]{cc}R_{t}^{2}&R_{t}\\ R_{t}&1\end{array}\right).$

Zatem

$\Sigma _{{xx}}=E(X_{t}^{T}X_{t})=\left(\begin{array}[]{cc}E(R_{t}^{2})&E(R_{t})\\ E(R_{t})&1\end{array}\right).$

Warunek maksymalnego rzędu jest spełniony gdyż

$det(\Sigma _{{xx}})=E(R_{t}^{2})-E(R_{t})^{2}=D^{2}(R_{t})>0.$

Warunek Z̃4.
Kładziemy

$g_{t}=\varepsilon _{t}(R_{t},1)=(R_{t}\eta _{{t+1}},\eta _{{t+1}}).$

$E(\eta _{{t+1}})=0$ podobnie

$E(R_{t}\eta _{{t+1}})=E(E(R_{t}\eta _{{t+1}}|{\cal I}_{{t}}))=E(R_{t}E(\eta _{{t+1}}|{\cal I}_{{t}}))=E(0)=0.$

Zatem $E(g_{t})=0$ czyli spełniony jest warunek ortogonalności.

Warunek Z̃5.
Zauważmy, że dla każdego $s$ zmienna losowa $g_{s}$ jest ${\cal I}_{{s+1}}$ mierzalna, a więc

${\cal I}_{{t}}\supset\sigma(g_{{t-1}},g_{{t-2}},\dots).$

Zatem

$E(g_{t}|g_{{t-1}},\dots)=E(E(g_{t}|{\cal I}_{{t}})|g_{{t-1}},\dots))=E(0)=0,$

czyli proces $\{ g_{t}\}$ jest ciągiem przyrostów martyngałowych.

Warunek Z̃6.
Warunkową homoskedastyczność przyjmujemy dla uproszczenia analizy modelu. Tym samym przyjmujemy odwracalność macierzy $\Sigma _{{gg}}$ .

Na podstawie badanej próbki wyznaczamy estymator MNK parametrów $\beta _{1}$ i $\beta _{2}$

$B\approx(1{,}0147,-0{,}8678).$

Błąd standardowy $B_{1}$ wynosi 0,1227 zatem statystyka testowa

$t_{1}=\frac{B_{1}-1}{SB_{1}}\approx 0{,}12.$

Zatem $p$ -wartość wynosi około 90%, czyli bez problemu możemy zaakceptować hipotezę $H_{0}$ .

12.3.3. Dyskusja wyników

Omówione powyżej testy potwierdzają hipotezę o efektywności rynku bonów w latach 1953 – 1971. Obserwacje w latach następnych nie potwiedziły już tej własności rynku. Można to tłumaczyć
$\bullet$ dużymi skokami inflacji
$\bullet$ i zdecydowaną interwencją FED na rynku.

Zauważmy ponadto, że powyższy przykład nie może być modelowany w terminach klasycznego modelu regresji gdyż nie jest spełniony warunek ścisłej egzogeniczności Z2.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Ekonometria

Zagadnienia

12. Hipoteza efektywnego rynku - ekonometria racjonalnych oczekiwań

12.1. Przykład E.Fama - konstrukcja modelu

12.2. Hipoteza efektywnego rynku

Lemat 12.1

Wniosek 12.1

12.3. Analiza danych empirycznych

12.3.1. Test na autokorelację realnych stóp zwrotu

12.3.2. Test predykcji stopy inflacji w oparciu o nominalną stopę zwrotu

12.3.3. Dyskusja wyników

12.3.2. Test predykcji stopy inflacji $\pi$ w oparciu o nominalną stopę zwrotu $R$