Zagadnienia

14.1 Szeregi czasowe stacjonarne rzędu 2
14.2 Sploty vel filtry
14.3 Funkcje tworzące
14.4 Operator przesunięcia
14.5 Przykłady
14.6 Procesy o przyrostach stacjonarnych
14.7 Ułamkowy ruch Browna

14. Liniowe szeregi czasowe

Stacjonarność rzędu 2. Funkcje tworzące. Klasyczne modele liniowe MA, AR, ARMA i ARIMA. Ułamkowe ruchy Browna. (1 wykład)

14.1. Szeregi czasowe stacjonarne rzędu 2

Na początek ustalmy przestrzeń probabilistyczną

$(\Omega,{\cal F},P).$

Przez $L^{2}(\Omega)$ będziemy oznaczać zbiór zmiennych losowych $X$ takich, że $E(X^{2})<\infty$ . Jak łatwo zauważyć jest to przestrzeń liniowa nad $\mathbb{R}$ . Ponadto, gdy utożsamimy zmienne losowe, które są prawie wszędzie równe to funkcja

$\| X\| _{{L^{2}}}=\sqrt{E(X^{2})}$

jest normą, a $L^{2}(\Omega)/\!\sim\;\;$ jest przestrzenią Banacha (por. [9] dodatek C.5 lub [3] §2.10).

Dla ustalenia uwagi przyjmiemy następującą definicję szeregu czasowego.

Definicja 14.1

Szeregiem czasowym nazywamy ciąg zmiennych losowych $X_{t}$ o wartościach rzeczywistych, $t\in\mathbb{Z}$

$\dots,X_{{-n}},\dots,X_{{-1}},X_{0},X_{1},\dots,X_{n},\dots.$

Definicja 14.2

Szereg czasowy $X_{t}$ nazywamy stacjonarnym rzędu 2 gdy

	a.		$\displaystyle\forall t\;\;\; X_{t}\in L^{2}(\Omega);$
	b.		$\displaystyle\forall t_{1},t_{2}\;\;\; E(X_{{t_{1}}})=E(X_{{t_{2}}});$
	c.		$\displaystyle\forall t_{1},t_{2},n\;\;\; cov(X_{{t_{1}+n}},X_{{t_{2}+n}})=cov(X_{{t_{1}}},X_{{t_{2}}}).$

Zauważmy, że czasami stacjonarność rzędu 2 implikuje silną stacjonarność.

Lemat 14.1

Gaussowski szereg czasowy stacjonarny rzędu 2 jest silnie stacjonarny w sensie definicji 8.6.

Dowód.
Jeśli $X_{t}$ jest procesem Gaussowskim to dla kazdego $s>0$ łączny rozkład $(X_{1},\dots,X_{s})$ jest rozkładem normalnym $N(\mu,\Sigma)$ , gdzie

$\mu _{1}=\dots=\mu _{s}=E(X_{1}),\;\;\;\Sigma _{{i,j}}=cov(X_{i},X_{j}).$

Podobnie dla dowolnego $n$ łączny rozkład $(X_{{n+1}},\dots,X_{{n+s}})$ jest rozkładem normalnym $N(\mu^{\prime},\Sigma^{\prime})$ , gdzie

$\mu^{\prime}_{1}=\dots=\mu^{\prime}_{s}=E(X_{{n+1}}),\;\;\;\Sigma^{\prime}_{{i,j}}=cov(X_{{n+i}},X_{{n+j}}).$

Ponieważ

$E(X_{{n+1}})=E(X_{1}),\;\;\;\mbox{ i }\;\;\; cov(X_{{n+i}},X_{{n+j}})=cov(X_{{i}},X_{{j}}),$

to oba rozkłady są identyczne.

Podstawowymi narzędziami służącymi do opisu stacjonarnych szeregów czasowych są funkcje autokowariancji. Dla każdego stacjonarnego rzędu 2 szeregu czasowego $\{ X_{t}\} _{{t=-\infty}}^{{+\infty}}$ definiujemy funkcję $\gamma$

$\gamma:\mathbb{Z}\longrightarrow\mathbb{R},$

przyporządkowującą liczbie całkowitej $k$ - $k$ -ty współczynnik autokowariancji (patrz definicja 11.1)

$\gamma(k)=cov(X_{0},X_{k}).$

Zauważmy, że ze stacjonarności wynika, że dla każdego $n$

$cov(X_{{n}},X_{{n+k}})=\gamma(k),$

a w szczególności

$D^{2}(X_{n})=\gamma(0).$

Twierdzenie 14.1

Niech $k\geq 0$ , wówczas funkcja autokowariancji stacjonarnego szeregu czasowego spełnia następujące warunki

	1.		$\displaystyle\gamma(-k)=\gamma(k);$
	2.		$\displaystyle\gamma(0)\geq 0;$
	3.		$\displaystyle\|\gamma(k)\|\leq\gamma(0);$
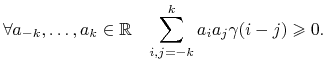	4.		$\displaystyle\forall a_{{-k}},\dots,a_{k}\in\mathbb{R}\;\;\;\sum _{{i,j=-k}}^{k}a_{i}a_{j}\gamma(i-j)\geq 0.$

Uwaga 14.1

Funkcje spełniające warunek 4 dla każdego $k$ nazywa się dodatnio określonymi.

Dowód.
Punkt 1 wynika z symetrii kowariancji.

$\gamma(-k)=cov(X_{0},X_{{-k}})=cov(X_{{-k}},X_{0})=cov(X_{0},X_{k})=\gamma(k).$

Punkt 2 jest oczywisty.

$\gamma(0)=cov(X_{0},X_{0})=D^{2}(X_{0})\geq 0.$

Punkt 3 wynika ze związków między korelacją i kowariancją.

$\gamma(k)^{2}=cov(X_{0},X_{k})^{2}\leq D^{2}(X_{0})D^{2}(X_{k})=\gamma(0)^{2}.$

Punkt 4 wynika z nieujemności wariancji zmiennej losowej. Rozważmy zmienną losową

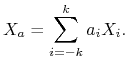$X_{a}=\sum _{{i=-k}}^{k}a_{i}X_{i}.$

Korzystając z dwuliniowości kowariancji otrzymujemy

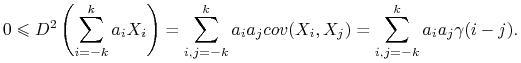$0\leq D^{2}\left(\sum _{{i=-k}}^{k}a_{i}X_{i}\right)=\sum _{{i,j=-k}}^{k}a_{i}a_{j}cov(X_{i},X_{j})=\sum _{{i,j=-k}}^{k}a_{i}a_{j}\gamma(i-j).$

Prawdziwe jest również twierdzenie odwrotne.

Twierdzenie 14.2

Jeśli funkcja $\gamma:\mathbb{Z}\rightarrow\mathbb{R}$ spełnia warunki 1,2,3 i 4 z powyższego twierdzenia to jest ona funkcją autokowariancji pewnego stacjonarnego szeregu czasowego.

Dowód
Patrz – [3] Theorem 1.5.1.

Zachowanie się funkcji autokowariancji dla dużych $n$ ma istotne znaczenie w praktycznych zastosowaniach. Wyróżnia się dwie klasy szeregów czasowych stacjonarnych rzędu 2.

Definicja 14.3

Niech $X$ będzie szeregiem czasowym stacjonarnym rzędu 2, a $\gamma _{X}$ jego funkcją autokowariancji.
Gdy $\gamma _{X}(n)$ zbiega do zera dla dużych $n$ w sposób wykładniczy

$\exists C>0\;\;\;\exists\delta\in(0,1)\;\;\;|\gamma _{X}(n)|<C\delta^{n},$

to mówimy, że $X$ jest procesem o krótkiej pamięci.
W przeciwnym przypadku mówimy, że $X$ jest procesem o długiej pamięci.

Gdy szereg czasowy nie jest prawie na pewno stały czyli gdy $\gamma(0)>0$ to definiujemy dodatkowo funkcję autokorelacji

$\rho:\mathbb{Z}\longrightarrow[-1,1],\;\;\;\rho(k)=\frac{\gamma(k)}{\gamma(0)}.$

Kluczowym obiektem w teorii szeregów czasowych stacjonarnych rzędu 2 jest biały szum. Jest to przykład procesu o (bardzo!) krótkiej pamięci.

Definicja 14.4

Stacjonarny rzędu 2 szereg czasowy $\varepsilon$ nazywamy białym szumem gdy

$E(X_{0})=0\;\;\;\gamma(0)>0\;\;\;\mbox{ i}\;\;\gamma(t)=0\;\;\;\mbox{ dla }t\neq 0.$

Gdy dodatkowo $\gamma(0)=1$ to $\varepsilon$ nazywamy unormowanym białym szumem.

Zbiór szeregów czasowych będących białym szumem o wariancji $\sigma^{2}=\gamma(0)$ będziemy oznaczać $WN(\sigma^{2})$ .

Uwaga 14.2

Kolejne wyrazy białego szumu są nieskorelowane ale nie muszą być niezależne, chyba, że jest to gaussowski biały szum.

14.2. Sploty vel filtry

Na początek przypomnimy, kiedy ciąg liczb rzeczywistych jest klasy $l^{p}$ .

Definicja 14.5

Ciąg $(a_{n})_{{n=0}}^{\infty}$ należy do klasy $l^{p}$ gdy jest sumowalny w $p$ -tej potędze.

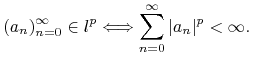$(a_{n})_{{n=0}}^{\infty}\in l^{p}\Longleftrightarrow\sum _{{n=0}}^{\infty}|a_{n}|^{p}<\infty.$

Uwaga 14.3

Zauważmy, że $l^{2}$ zawiera $l^{1}$ . Ponadto dla $p\geq 1$ klasy $l^{p}$ są unormowanymi przestrzeniami liniowymi

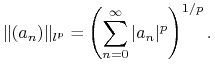$\|(a_{n})\| _{{l^{p}}}=\left(\sum _{{n=0}}^{\infty}|a_{n}|^{p}\right)^{{1/p}}.$

Definicja 14.6

Niech $X=(X_{t})_{{t=-\infty}}^{{+\infty}}$ będzie szeregiem czasowym, a $a=(a_{n})_{{n=0}}^{\infty}$ ciągiem o wyrazach rzeczywistych. Wówczas szereg czasowy $Y=(Y_{t})_{{t=-\infty}}^{{+\infty}}$ , którego wyrazy dają się przedstawić jako sumy nieskończone w $L^{2}(\Omega)$

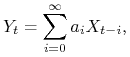$Y_{t}=\sum _{{i=0}}^{\infty}a_{i}X_{{t-i}},$

nazywamy splotem ciągu $a$ i szeregu $X$ .

Operację splotu będziemy oznaczać przez ” $\star$ ”

$Y=a\star X.$

Uwaga 14.4

W niektórych źródłach operację splotu z ciągiem $(a_{n})$ nazywa się filtrem o współczynnikach $a_{n}$ .

Podamy teraz dwa warunki gwarantujące istnienie splotu $(Y_{t})$ ciągu $a=(a_{n})$ i szeregu $(X_{t})$ .

Twierdzenie 14.3

Jeżeli zachodzi jeden z poniższych warunków

	1.		$\displaystyle(a_{n})\in l^{1}\;\;\;\mbox{ i }\;\;\;\forall t\in\mathbb{Z}\;\;\;\|E(X_{t})\|\leq\mu,\;\;\; D^{2}(X_{t})\leq\sigma^{2}.$
	2.		$\displaystyle(a_{n})\in l^{2},\;\;\;\forall t\in\mathbb{Z}\;\;\; E(X_{t})=0,\;\;\; D^{2}(X_{t})\leq\sigma^{2},\;\;\;\mbox{ oraz }\;\;\; X_{t}\mbox{ nieskorelowane ze sobą.}$

to istnieje splot ciągu $a=(a_{n})$ i szeregu $(X_{t})$ .

Dowód.
Skorzystamy z zasady majoryzacji.
Ad 1.

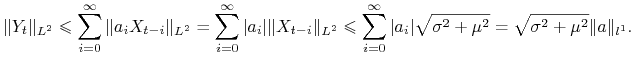$\| Y_{t}\| _{{L^{2}}}\leq\sum _{{i=0}}^{\infty}\| a_{i}X_{{t-i}}\| _{{L^{2}}}=\sum _{{i=0}}^{\infty}|a_{i}|\| X_{{t-i}}\| _{{L^{2}}}\leq\sum _{{i=0}}^{\infty}|a_{i}|\sqrt{\sigma^{2}+\mu^{2}}=\sqrt{\sigma^{2}+\mu^{2}}\| a\| _{{l^{1}}}.$

Ad 2.

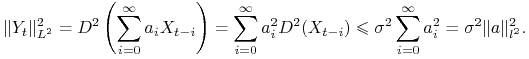$\| Y_{t}\| _{{L^{2}}}^{2}=D^{2}\left(\sum _{{i=0}}^{\infty}a_{i}X_{{t-i}}\right)=\sum _{{i=0}}^{\infty}a_{i}^{2}D^{2}(X_{{t-i}})\leq\sigma^{2}\sum _{{i=0}}^{\infty}a_{i}^{2}=\sigma^{2}\| a\| _{{l^{2}}}^{2}.$

Twierdzenie 14.4

Gdy szereg czasowy $(X_{t})$ jest stacjonarny rzędu 2, a ciąg $a=(a_{n})$ należy do $l^{1}$ to ich splot $(Y_{t})$ jest stacjonarny rzędu 2.

Dowód.
Pokażemy, że wartość oczekiwana i autokowariancje szeregu $(Y_{t})$ nie zmieniają się przy przesunięciu. Oznaczmy przez $\mu$ wartość oczekiwaną $X_{t}$ a przez $\gamma _{X}$ funkcję autokowariancji.

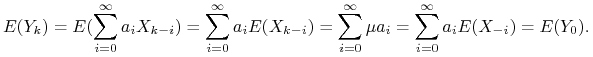$E(Y_{k})=E(\sum _{{i=0}}^{\infty}a_{i}X_{{k-i}})=\sum _{{i=0}}^{\infty}a_{i}E(X_{{k-i}})=\sum _{{i=0}}^{\infty}\mu a_{i}=\sum _{{i=0}}^{\infty}a_{i}E(X_{{-i}})=E(Y_{0}).$

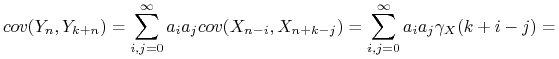$cov(Y_{n},Y_{{k+n}})=\sum _{{i,j=0}}^{\infty}a_{i}a_{j}cov(X_{{n-i}},X_{{n+k-j}})=\sum _{{i,j=0}}^{\infty}a_{i}a_{j}\gamma _{X}(k+i-j)=$

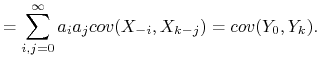$=\sum _{{i,j=0}}^{\infty}a_{i}a_{j}cov(X_{{-i}},X_{{k-j}})=cov(Y_{0},Y_{k}).$

Twierdzenie 14.5

Gdy szereg czasowy $(\varepsilon _{t})$ jest białym szumem, a ciąg $a=(a_{n})$ należy do $l^{2}$ to ich splot $(Y_{t})$ jest stacjonarny rzędu 2. Ponadto

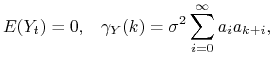$E(Y_{t})=0,\;\;\;\gamma _{Y}(k)=\sigma^{2}\sum _{{i=0}}^{\infty}a_{i}a_{{k+i}},$

gdzie $\sigma^{2}$ wariancja $\varepsilon _{0}$ .

Dowód.
Powtarzamy rozumowanie z poprzedniego dowodu i wstawiamy $E(\varepsilon _{t})=0$ oraz $\gamma _{{\varepsilon}}(0)=\sigma^{2}$ i $\gamma _{{\varepsilon}}(t)=0$ dla $t\neq 0$ .

Okazuje się, że z dokładnością do pewnego ”nieistotnego” składnika, wszystkie szeregi czasowe stacjonarne rzędu 2 można przedstawić w postaci splotu z białym szumem.

Twierdzenie 14.6

Niech $X$ będzie szeregiem czasowym stacjonarnym rzędu 2 o zerowej wartości oczekiwanej, $E(X_{0})=0$ . Wówczas istnieją ciąg $a$ klasy $l^{2}$ i unormowany biały szum $\varepsilon$ takie, że

$X=a\star\epsilon+V,$

gdzie szereg czasowy $V$ jest nieskorelowany z $\varepsilon$

$\forall s,t\;\;\; E(V_{s}\varepsilon _{t})=0$

i ponadto jest zawarty w przecięciu domknięć (w $L^{2}$ ) podprzestrzeni generowanych przez początkowe $X_{s}$

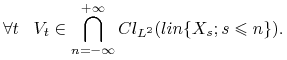$\forall t\;\;\; V_{t}\in\bigcap _{{n=-\infty}}^{{+\infty}}Cl_{{L^{2}}}(lin\{ X_{s};s\leq n\}).$

Dowód.
Powyższe twierdzenie jest wnioskiem z ”rozkładu Wolda” - [3] Theorem 5.7.1.

Operacja splotu przeprowadza szeregi czasowe stacjonarne rzędu 2 na szeregi czasowe stacjonarne rzędu 2. Zatem sploty można iterować.

Twierdzenie 14.7

Niech ciągi $a$ i $b$ należą do przestrzeni $l^{1}$ , a $X$ będzie szeregiem czasowym stacjonarnym rzędu 2. Wówczas

$a\star(b\star X)=c\star X,$

gdzie $c$ jest ciągiem o wyrazach

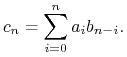$c_{n}=\sum _{{i=0}}^{n}a_{i}b_{{n-i}}.$

Uwaga 14.5

Ciąg $c$ z powyższego twierdzenia nazywa się iloczynem Cauchy'ego ciągów $a$ i $b$ . Jak łatwo sprawdzić $c$ też należy do $l^{1}$ . Zatem splot definiuje działanie algebry $l^{1}$ na zbiorze szeregów czasowych, które są stacjonarne rzędu 2. Ponadto mnożenie Cauchy'ego jest przemienne gdyż

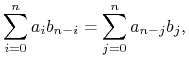$\sum _{{i=0}}^{n}a_{i}b_{{n-i}}=\sum _{{j=0}}^{n}a_{{n-j}}b_{{j}},$

zatem dla $a,b\in l^{1}$

$b\star(a\star X)=a\star(b\star X).$

Dowód twierdzenia.
Oznaczmy przez $Y$ splot $b$ i $X$ , a przez $Z$ splot $a$ i $Y$ . Wówczas

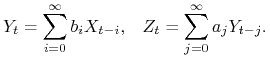$Y_{t}=\sum _{{i=0}}^{{\infty}}b_{i}X_{{t-i}},\;\;\; Z_{t}=\sum _{{j=0}}^{{\infty}}a_{j}Y_{{t-j}}.$

Przedstawiamy szereg $Z$ w zależności od szeregu $X$

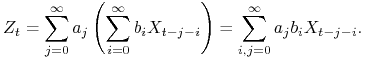$Z_{t}=\sum _{{j=0}}^{{\infty}}a_{j}\left(\sum _{{i=0}}^{{\infty}}b_{i}X_{{t-j-i}}\right)=\sum _{{i,j=0}}^{{\infty}}a_{j}b_{i}X_{{t-j-i}}.$

Podstawiamy $k=i+j$ i porządkujemy powyższą sumę względem $X_{{t-k}}$ .

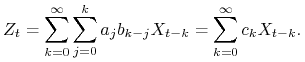$Z_{t}=\sum _{{k=0}}^{\infty}\sum _{{j=0}}^{k}a_{j}b_{{k-j}}X_{{t-k}}=\sum _{{k=0}}^{\infty}c_{k}X_{{t-k}}.$

Gdy szereg $X$ z twierdzenia 14.7 jest białym szumem to możemy osłabić założenia dotyczące ciągu $b$ . W analogiczny sposób jak twierdzenie 14.7 dowodzi się następujące twierdzenie.

Twierdzenie 14.8

Niech ciąg $a$ należy do przestrzeni $l^{1}$ , ciąg $b$ do $l^{2}$ , a $\varepsilon$ będzie białym szumem. Wówczas

$a\star(b\star\varepsilon)=c\star\varepsilon,$

gdzie $c$ jest ciągiem o wyrazach

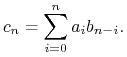$c_{n}=\sum _{{i=0}}^{n}a_{i}b_{{n-i}}.$

14.3. Funkcje tworzące

Mnożenie Cauchy'ego ciągów jest ściśle związane z mnożeniem szeregów potęgowych. Otóż

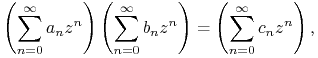$\left(\sum _{{n=0}}^{\infty}a_{n}z^{n}\right)\left(\sum _{{n=0}}^{\infty}b_{n}z^{n}\right)=\left(\sum _{{n=0}}^{\infty}c_{n}z^{n}\right),$

gdzie ciąg $c$ jest iloczynem Cauchy'ego ciągów $a$ i $b$

$c_{n}=\sum _{{i=0}}^{n}a_{i}b_{{n-i}}.$

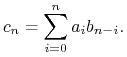Dlatego przyporządkujemy ciągom funkcje tworzące czyli sumy szeregów potęgowych. Pozwala to wykorzystać aparat analizy zespolonej do badania szeregów czasowych.

Definicja 14.7

Funkcję holomorficzną

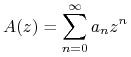$A(z)=\sum _{{n=0}}^{\infty}a_{n}z^{n}$

nazywamy funkcją tworzącą ciągu liczbowego $a=(a_{n})_{{n=0}}^{\infty}$ .

Zauważmy, że istnieje zależność między promieniem zbieżności $R_{A}$ szeregu potęgowego $A(z)$ a klasą ciągu $a$ .

Lemat 14.2

	$\displaystyle R_{A}>1$	$\displaystyle\Longrightarrow$	$\displaystyle a\in l^{1},$
	$\displaystyle R_{A}<1$	$\displaystyle\Longrightarrow$	$\displaystyle a\not\in l^{2}.$

Dowód.
Gdy promień zbieżności szeregu potęgowego $A$ jest większy od 1 to jest on zbieżny bezwzględnie w punkcie $z_{\ast}=1$ . Zatem

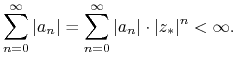$\sum _{{n=0}}^{\infty}|a_{n}|=\sum _{{n=0}}^{\infty}|a_{n}|\cdot|z_{\ast}|^{n}<\infty.$

Natomiast gdy ciąg $a$ jest klasy $l^{2}$ to musi on zbiegać do 0

$\lim _{{n\rightarrow\infty}}a_{n}=0.$

Zatem

$\limsup _{{n\rightarrow\infty}}\sqrt[n]{a_{n}}\leq 1.$

Z czego wynika, że promień zbieżności szeregu potęgowego $A$ jest nie mniejszy niż 1

$R_{A}=\left(\limsup _{{n\rightarrow\infty}}\sqrt[n]{a_{n}}\right)^{{-1}}\geq 1.$

Więc jeśli promień zbieżności $R_{A}$ jest mniejszy od 1, to ciąg $a$ nie należy do $l^{2}$ .

Funkcje tworzące dla funkcji autokowariancji określamy jako sumy szeregów Laurenta (por. [15] Cz. I, §6).

Definicja 14.8

Funkcję holomorficzną

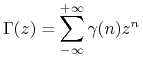$\Gamma(z)=\sum _{{-\infty}}^{{+\infty}}\gamma(n)z^{n}$

określoną na pierścieniu

$\frac{1}{r}<|z|<r,\;\;\; r>1,$

nazywamy funkcją tworzącą ciągu liczbowego $\gamma=(\gamma(n))_{{-\infty}}^{{+\infty}}$ .

Uwaga 14.6

Współczynniki rozwinięcia funkcji $\Gamma$ w szereg Laurenta na pierścieniu

$\frac{1}{r}<|z|<r,\;\;\; r>1,$

są wyznaczone jednoznacznie (por. [15] Cz. I, §6, Twierdzenie 2).

Lemat 14.3

Niech $\gamma$ będzie funkcją autokowariancji szeregu czasowego $X$ stacjonarnego rzędu 2. Wówczas następujące warunki są równoważne:
1. Szereg Laurenta $\Gamma(z)$ jest zbiezny w pewnym pierścieniu

$\frac{1}{r}<|z|<r,\;\;\; r>1.$

2. Szereg czasowy $X$ jest procesem o krótkiej pamięci.

Dowód.
$1\Rightarrow 2$ .
Z nierówności Cauchy'ego dla współczynników szeregu Laurenta ([15] s.120) otrzymujemy, że dla każdego $\rho\in(1,r)$

$\forall n\;\;\;|\gamma(n)|\leq\frac{M}{\rho^{n}},$

gdzie $M$ to maksimum modułu funkcji $\Gamma$ na okręgu $|z|=\rho$ .

$2\Rightarrow 1$ .
Gdy szereg czasowy $X$ jest procesem o krótkiej pamięci to istnieją stałe $C$ i $\delta$ , $C>0$ , $\delta\in(0,1)$ , takie, że

$\forall n\;\;\;|\gamma(n)|<C\delta^{{|n|}}.$

Zatem

$\limsup _{{n\rightarrow\infty}}\sqrt[n]{\gamma(-n)}=\limsup _{{n\rightarrow\infty}}\sqrt[n]{\gamma(n)}\leq\delta<1.$

Zatem szereg Laurenta $\Gamma(z)$ jest zbieżny na pierścieniu

$\delta<|z|<\frac{1}{\delta}$

(por. [15] s.117).

14.4. Operator przesunięcia

Oznaczymy przez $L$ operator przesunięcia szeregu czasowego o 1 w prawo

$Y=L(X)\;\;\;\Longleftrightarrow\;\;\;\forall t\in\mathbb{Z}\;\;\; Y_{t}=X_{{t-1}}.$

Pozwoli to nam zapisać splot $Y=a\star X$ jako szereg potęgowy iterowanych operatorów przesunięcia

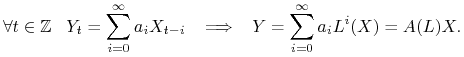$\forall t\in\mathbb{Z}\;\;\; Y_{t}=\sum _{{i=0}}^{\infty}a_{i}X_{{t-i}}\;\;\;\Longrightarrow\;\;\; Y=\sum _{{i=0}}^{\infty}a_{i}L^{i}(X)=A(L)X.$

Z twierdzeń 14.7 i 14.8 wynika następujący wniosek.

Wniosek 14.1

Funkcja tworząca złożenia operatorów $A_{1}(L)$ i $A_{2}(L)$ jest iloczynem funkcji $A_{1}(z)$ i $A_{2}(z)$

$A_{1}(L)\circ A_{2}(L)=(A_{1}\cdot A_{2})(L).$

Funkcja tworząca funkcji autokowariancji szeregu czasowego $X$ będącego obrazem unormowanego białego szumu $\varepsilon$ , $X=A(L)\varepsilon$ wynosi

$\Gamma(z)=A(z)A(z^{{-1}}).$

Uwaga 14.7

Gdy promień zbieżności szeregu potęgowego $A(z)$ jest większy od 1 to szereg $\Gamma(z)=A(z)A(z^{{-1}})$ jest zbieżny na pierścieniu

$\{ z:R_{A}^{{-1}}<|z|<R_{A}\}.$

Z powyższej uwagi i lematu 14.3 otrzymujemy:

Wniosek 14.2

Gdy promień zbieżności szeregu potęgowego $A(z)$ jest większy od 1 to szereg czasowy $X=A(L)\varepsilon$ , $\;\varepsilon\in WN(\sigma^{2})$ , jest procesem o krótkiej pamięci.

14.5. Przykłady

Przedstawimy teraz kilka najpopularniejszych szeregów czasowych stacjonarnych rzędu 2. Niech $\varepsilon=(\varepsilon _{t})_{{-\infty}}^{{+\infty}}$ będzie unormowanym białym szumem.

1. Wielomianowa funkcja tworząca.
Szereg czasowy $X$ postaci

$X=A(L)\varepsilon,$

gdzie $A(z)$ wielomian stopnia $p$ nazywa się szeregiem średnich ruchomych rzędu $p$ – $MA(p)$ .

$\forall t\;\;\; X_{t}=a_{0}\varepsilon _{t}+a_{1}\varepsilon _{{t-1}}+\dots+a_{p}\varepsilon _{{t-p}}.$

2. Funkcja tworząca jest odwrotnością funkcji wielomianowej.
Szereg czasowy $X$ postaci

$X=C(L)\varepsilon,\;\;\; C(z)=\frac{1}{B(z)},$

gdzie $B(z)$ wielomian stopnia $q$ , który nie zeruje się na kole jednostkowym

$|z|\leq 1\;\;\;\Longrightarrow\;\;\; B(z)\neq 0,$

nazywa się szeregiem autoregresyjnym rzędu $q$ – $AR(q)$ .
Szereg $X$ spełnia równanie

$B(L)X=\varepsilon,$

zatem

$\forall t\;\;\; b_{0}X_{t}+b_{1}X_{{t-1}}+\dots+b_{q}X_{{t-q}}=\varepsilon _{t}.$

3. Funkcja tworząca jest ilorazem funkcji wielomianowych.
Szereg czasowy $X$ postaci

$X=D(L)\varepsilon,\;\;\; D(z)=\frac{A(z)}{B(z)},$

gdzie $A(z)$ wielomian stopnia $p$ a $B(z)$ wielomian stopnia $q$ , który nie zeruje się na kole jednostkowym

$|z|\leq 1\;\;\;\Longrightarrow\;\;\; B(z)\neq 0,$

nazywa się autoregresyjnym szeregiem średnich ruchomych rzędu $(q,p)$ – $ARMA(q,p)$ .
Szereg $X$ spełnia równanie

$B(L)X=A(L)\varepsilon,$

zatem

$\forall t\;\;\; b_{0}X_{t}+b_{1}X_{{t-1}}+\dots+b_{q}X_{{t-q}}=a_{0}\varepsilon _{t}+a_{1}\varepsilon _{{t-1}}+\dots+a_{p}\varepsilon _{{t-p}}.$

Biorąc pod uwagę, że funkcje tworzące w trzech powyższych przykładach mają promień zbieżności większy od 1, to na mocy wniosku 14.2 otrzymujemy:

Lemat 14.4

Szeregi czasowe $MA$ , $AR$ i $ARMA$ są procesami o krótkiej pamięci.

Uwaga 14.8

Niech $\gamma$ będzie funkcją autokowariancji szeregu czasowego $X=A(L)\varepsilon$ , $\varepsilon\in WN(1)$ . Gdy $X$ jest klasy $AR$ to operator $A$ jest wyznaczony przez funkcje autokowariancji $\gamma$ z dokładnością do znaku. Natomiast dla szeregów czasowych $MA$ i $ARMA$ taka jednoznaczność zachodzi tylko przy dodatkowym warunku, że funkcje tworzące nie zerują się w kole jednostkowym.

Przykład $ARMA(1,1)$ .
Rozważmy szereg czasowy

$X=D(L)\varepsilon,\;\;\; D(z)=\frac{3z+1}{z+3},\;\;\;\varepsilon\in WN(1).$

Funkcja $D(z)$ jest holomorficzna na całej płaszczyźnie zespolonej poza punktem $z=-3$ gdzie ma biegun. Zatem promień zbieżności jej szeregu Taylora w 0 wynosi 3.
Okazuje się, że funkcja tworząca funkcji autokowariancji jest stała

$\Gamma(z)=D(z)D(z^{{-1}})=\frac{3z+1}{z+3}\frac{3z^{{-1}}+1}{z^{{-1}}+3}=\frac{3z+1}{z+3}\frac{3+1z}{1+3z}=1.$

Czyli szereg $X$ jest białym szumem. Zatem reprezentacja $ARMA$ szeregu czasowego o zadanej funkcji autokowariancji nie jest jednoznaczna.

14.6. Procesy o przyrostach stacjonarnych

Niech $Y$ będzie dowolnym szeregiem czasowym. Szereg $X$ taki, że

$\forall t\;\;\; X_{t}=Y_{t}-Y_{{t-1}},$

czyli

$X=(1-L)Y,$

nazywamy szeregiem przyrostów szeregu $Y$ .

Operację brania przyrostów można iterować. Szereg

$X=(1-L)^{k}Y=P(L)Y,\;\;\; P(z)=(1-z)^{k},$

nazywamy szeregiem $k$ -tych przyrostów szeregu $Y$ .

Gdy $k$ -te przyrosty szeregu czasowego $Y$ są stacjonarne rzędu 2 i należą do klasy $ARMA(q,p)$ to mówimy, że szereg $Y$ jest klasy $ARIMA(q,k,p)$ .

Przykłady
$\bullet$ Błądzenie przypadkowe bez dryfu

$X_{t}=X_{{t-1}}+\sigma\varepsilon _{t}$

jest procesem klasy $ARIMA(0,1,0)$ .

$\bullet$ Błądzenie przypadkowe z dryfem

$X_{t}=X_{{t-1}}+\mu+\sigma\varepsilon _{t}$

jest procesem klasy $ARIMA(0,2,1)$ .

$\bullet$ Trend liniowy

$X_{t}=at+b+\sigma\varepsilon _{t}$

jest procesem klasy $ARIMA(0,2,2)$ .

$\bullet$ Trend wielomianowy stopnia $k$

$X_{t}=a_{k}t^{k}+a_{{k-1}}t^{{k-1}}+\dots a_{0}+\sigma\varepsilon _{t}$

jest procesem klasy $ARIMA(0,k+1,k+1)$ .

14.7. Ułamkowy ruch Browna

Definicja 14.9

Gaussowski proces $B_{t}^{H}$ , $\; t\in\mathbb{Z}$ , $\; H\in(0,1)$ , taki, że

$\forall t\;\;\; E(X_{t})=0;$

$\forall t,s\;\;\; cov(B_{t}^{H},B_{s}^{H})=\frac{\sigma^{2}}{2}\left(|t|^{{2H}}+|s|^{{2H}}-|t-s|^{{2H}}\right),\;\;\;\sigma>0,$

nazywamy ułamkowym ruchem Browna.

Pokażemy, że szereg $B^{H}$ jest procesem o przyrostach stacjonarnych. Niech

$X_{t}=B^{H}_{t}-B^{H}_{{t-1}}.$

Lemat 14.5

Szereg czasowy $X^{H}_{t}$ jest stacjonarny o zerowej wartości oczekiwanej, $E(X^{H}_{t})=0$ , oraz funkcji autokowariancji

$\gamma(n)=\frac{\sigma^{2}}{2}\left(|n+1|^{{2H}}+|n-1|^{{2H}}-2|n|^{{2H}}\right).$

Dowód.
Ponieważ $B^{H}$ jest szeregiem o zerowej wartości oczekiwanej to to samo zachodzi dla szeregu przyrostów. Natomiast

$cov(X^{H}_{t},X^{H}_{{t+n}})=cov(B^{H}_{t}-B^{H}_{{t-1}},B^{H}_{{t+n}}-B^{H}_{{t+n-1}})=$

$=\frac{\sigma^{2}}{2}\left((|t|^{{2H}}+|t+n|^{{2H}}-|n|^{{2H}})+(|t-1|^{{2H}}+|t+n-1|^{{2H}}-|n|^{{2H}})\right.-$

$\left.-(|t+n|^{{2H}}+|t-1|^{{2H}}-|n+1|^{{2H}})-(|t+n-1|^{{2H}}+|t|^{{2H}}-|n-1|^{{2H}})\right)=$

$=\frac{\sigma^{2}}{2}\left(|n+1|^{{2H}}+|n-1|^{{2H}}-2|n|^{{2H}}\right).$

Zatem $X^{H}$ jest stacjonarny z funkcją autokowariancji

$\gamma(n)=\frac{\sigma^{2}}{2}\left(|n+1|^{{2H}}+|n-1|^{{2H}}-2|n|^{{2H}}\right).$

Uwaga 14.9

Dla wszystkich $X^{H}$ $\;\;\gamma(0)=\sigma^{2}$ . Dodatkowo dla $H=\frac{1}{2}$ i $n\neq 0$ $\;\;\gamma(n)=0$ . Zatem $X^{{1/2}}$ jest gaussowskim białym szumem, a $B^{{1/2}}$ jest gaussowskim błądzeniem przypadkowym.

Lemat 14.6

Dla $H\neq\frac{1}{2}$

$\lim _{{n\rightarrow\infty}}\gamma(n)n^{{2-2H}}=H(2H-1)\sigma^{2}.$

Dowód.
Dla $n>1$

$\frac{\gamma(n)}{\sigma^{2}}=\frac{1}{2}\left((n+1)^{{2H}}+(n-1)^{{2H}}-2n^{{2H}}\right)=\frac{n^{{2H}}}{2}\left((1+\frac{1}{n})^{{2H}}+(1-\frac{1}{n})^{{2H}}-2\right)=$

$=\frac{n^{{2H}}}{2}\left(1+\frac{2H}{n}+\frac{2H(2H-1)}{2n^{2}}+1-\frac{2H}{n}+\frac{2H(2H-1)}{2n^{2}}-2+O(n^{{-3}})\right)=$

$=H(2H-1)n^{{2H-2}}+O(n^{{2H-3}}).$

Uwaga 14.10

Gdy $H\neq\frac{1}{2}$ , to szereg czasowy $X^{H}$ jest procesem stacjonarnym o długiej pamięci.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Ekonometria

Zagadnienia

14. Liniowe szeregi czasowe

14.1. Szeregi czasowe stacjonarne rzędu 2

Definicja 14.1

Definicja 14.2

Lemat 14.1

Twierdzenie 14.1

Uwaga 14.1

Twierdzenie 14.2

Definicja 14.3

Definicja 14.4

Uwaga 14.2

14.2. Sploty vel filtry

Definicja 14.5

Uwaga 14.3

Definicja 14.6

Uwaga 14.4

Twierdzenie 14.3

Twierdzenie 14.4

Twierdzenie 14.5

Twierdzenie 14.6

Twierdzenie 14.7

Uwaga 14.5

Twierdzenie 14.8

14.3. Funkcje tworzące

Definicja 14.7

Lemat 14.2

Definicja 14.8

Uwaga 14.6

Lemat 14.3

14.4. Operator przesunięcia

Wniosek 14.1

Uwaga 14.7

Wniosek 14.2

14.5. Przykłady

Lemat 14.4

Uwaga 14.8

14.6. Procesy o przyrostach stacjonarnych

14.7. Ułamkowy ruch Browna

Definicja 14.9

Lemat 14.5

Uwaga 14.9

Lemat 14.6

Uwaga 14.10