Zagadnienia

2.1 Wprowadzenie
2.2 Odrobina algebry liniowej

2. Metoda najmniejszych kwadratów (MNK)

Metoda najmniejszych kwadratów (MNK). Sformułowanie zadania. Wyznaczanie optymalnych wartości parametrów. Oszacowanie błędu przybliżenia. Algebraiczne własności MNK. (1 wykład)

2.1. Wprowadzenie

Zadanie.
Dane jest $m+1$ ciągów $n$ -elementowych o wyrazach rzeczywistych:

$\displaystyle Y$	$\displaystyle=$	$\displaystyle(Y_{t})_{{t=1,\dots,n}}$
$\displaystyle X_{1}$	$\displaystyle=$	$\displaystyle(X_{{t,1}})_{{t=1,\dots,n}}$
$\displaystyle X_{2}$	$\displaystyle=$	$\displaystyle(X_{{t,2}})_{{t=1,\dots,n}}$
	$\displaystyle\dots$
$\displaystyle X_{m}$	$\displaystyle=$	$\displaystyle(X_{{t,m}})_{{t=1,\dots,n}}.$

Wyznaczyć współczynniki $b_{1},\dots,b_{m}\in\mathbb{R}$ , które minimalizują błąd przybliżenia $Y$ przez kombinację liniową $\widehat{Y}$

$\widehat{Y}_{t}=b_{1}X_{{t,1}}+\dots+b_{m}X_{{t,m}}.$

Czyli mamy rozwiązać zadanie optymalizacyjne

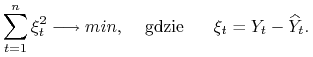$\sum _{{t=1}}^{n}\xi _{t}^{2}\longrightarrow min,\;\;\;\mbox{ gdzie }\;\;\;\;\;\xi _{t}=Y_{t}-\widehat{Y}_{t}.$

W zastosowaniach ekonometrycznych $\widehat{Y}$ nazywa się zmienną modelową w odróżnieniu od zmiennej empirycznej $Y$ .

W dalszym ciągu będziemy stosować zapis macierzowy:
$Y$ będzie zapisywać jako wektor kolumnowy czyli macierz $n\times 1$

$Y=\left(\begin{array}[]{l}Y_{1}\\ \dots\\ Y_{n}\end{array}\right),$

$X$ jako macierz $n\times m$ , której kolumnami są $X_{i}$

$X=\left(\begin{array}[]{llll}X_{{1,1}}&X_{{1,2}}&\dots&X_{{1,m}}\\ X_{{2,1}}&X_{{2,2}}&\dots&X_{{2,m}}\\ \dots&\dots&\dots&\dots\\ X_{{n,1}}&X_{{n,2}}&\dots&X_{{n,m}}\end{array}\right),$

szukane parametry $b_{i}$ jako wektor kolumnowy $m\times 1$

$B=\left(\begin{array}[]{l}b_{1}\\ \dots\\ b_{m}\end{array}\right),$

podobnie składnik resztowy (residualny) $\xi$ jako wektor kolumnowy $n\times 1$

$\xi=\left(\begin{array}[]{l}\xi _{1}\\ \dots\\ \xi _{n}\end{array}\right).$

Wówczas możemy zapisać

$\widehat{Y}=XB,\;\;\;\xi=Y-\widehat{Y}=Y-XB.$

Suma kwadratów reszt (SKR) wynosi

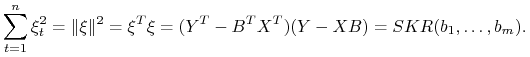$\sum _{{t=1}}^{n}\xi _{t}^{2}=\|\xi\|^{2}=\xi^{T}\xi=(Y^{T}-B^{T}X^{T})(Y-XB)=SKR(b_{1},\dots,b_{m}).$

Zauważmy, że funkcja

$SKR:\mathbb{R}^{m}\longrightarrow\mathbb{R}$

jest funkcją kwadratową o wartościach nieujemnych, a zatem osiąga swoje minimum.

Twierdzenie 2.1

Jeżeli ciągi $X_{1}$ , … , $X_{m}$ są liniowo niezależne to $SKR$ przyjmuje minimum dokładnie w jednym punkcie

$B_{{min}}=(X^{T}X)^{{-1}}X^{T}Y.$

(2.1)

Minimum to wynosi

$SKR_{{min}}=SKR(B_{{min}})=Y^{T}Y-Y^{T}X(X^{T}X)^{{-1}}X^{T}Y.$

Dowód.
Krok 1. Najpierw pokażemy, że macierz $X^{T}X$ jest odwracalna a zatem wzór 2.1 jest poprawny.

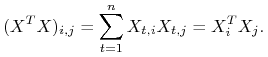$(X^{T}X)_{{i,j}}=\sum _{{t=1}}^{n}X_{{t,i}}X_{{t,j}}=X_{i}^{T}X_{j}.$

$m\times m$ macierz $X^{T}X$ jest macierzą Grama wektorów $X_{i}$ . Zatem jeżeli $X_{i}$ są liniowo niezależne to macierz $X^{T}X$ jest nieujemnie określona, a zatem odwracalna (por. [1] §VI.11 Wniosek 11.4).

Krok 2. Pokażemy, że $B_{{min}}$ to punkt w którym przyjmowane jest minimum globalne.

$B=B_{{min}}+b,\;\;\;\;\; b\neq 0,$

$SKR(B_{{min}}+b)=(Y^{T}-B_{{min}}^{T}X^{T}-b^{T}X^{T})(Y-XB_{{min}}-Xb)=$

$=(Y^{T}-B_{{min}}^{T}X^{T})(Y-XB_{{min}})-(Y^{T}-B_{{min}}^{T}X^{T})Xb-b^{T}X^{T}(Y-XB_{{min}})+b^{T}X^{T}Xb=$

$=SKR(B_{{min}})-2b^{T}X^{T}(Y-XB_{{min}})+b^{T}X^{T}Xb.$

Zauważmy, że drugi człon jest równy 0

$X^{T}(Y-XB_{{min}})=X^{T}(Y-X(X^{T}X)^{{-1}}X^{T}Y)=X^{T}Y-X^{T}X(X^{T}X)^{{-1}}X^{T}Y=0,$

a trzeci jest nieujemny dla niezerowych $b$ ponieważ macierz $X^{T}X$ jest nieujemnie określona. Zatem dla $b\neq 0$

$SKR(B_{{min}}+b)>SKR(B_{{min}}).$

Krok 3. Wyznaczamy $SKR(B_{{min}})$ .
Ponieważ jak pokazaliśmy powyżej $X^{T}(Y-XB_{{min}})=0$ to

$SKR(B_{{min}})=(Y^{T}-B_{{min}}^{T}X^{T})(Y-XB_{{min}})=Y^{T}(Y-XB_{{min}})=$

$=Y^{T}Y-Y^{T}XB_{{min}}=Y^{T}Y-Y^{T}X(X^{T}X)^{{-1}}X^{T}Y.$

$\Box$

Wniosek 2.1

Dla $B=B_{{min}}$ zachodzą następujące zależności:
1. Wektor składników resztowych $\xi$ jest prostopadły do wszystkich kolumn $X_{i}$

$X^{T}\xi=0.$

2. Wektor składników resztowych $\xi$ jest prostopadły do wektora $\widehat{Y}$

$\widehat{Y}^{T}\xi=0.$

3. Uogólnione twierdzenie Pitagorasa

$Y^{T}Y=\widehat{Y}^{T}\widehat{Y}+\xi^{T}\xi\;\;\mbox{ czyli }\;\;\;\| Y\|^{2}=\|\widehat{Y}\|^{2}+\|\xi\|^{2}.$

Dowód.
Ad 1. Z definicji $\xi$ mamy

$X^{T}\xi=X^{T}(Y-XB)=X^{T}(Y-X(X^{T}X)^{{-1}}X^{T}Y)=X^{T}Y-X^{T}X(X^{T}X)^{{-1}}X^{T}Y=0.$

Ad 2. $\widehat{Y}$ jest kombinacją liniową $X_{i}$ zatem

$\widehat{Y}^{T}\xi=B^{T}X^{T}\xi=0.$

Ad 3. Ponieważ $\xi$ i $\widehat{Y}$ są prostopadłe to

$Y^{T}Y=(\widehat{Y}^{T}+\xi^{T})(\widehat{Y}+\xi)=\widehat{Y}^{T}\widehat{Y}+\xi^{T}\xi.$

Uwaga 2.1

Gdy ciągi $X_{1}$ , … , $X_{m}$ są liniowo zależne to wybieramy spośród nich maksymalny podzbiór liniowo niezależny $X_{{j_{1}}}$ , … , $X_{{j_{k}}}$ ( $k=rank\; X<m$ ). Niech $\widetilde{X}$ będzie $n\times k$ macierzą, której kolumnami są $X_{{j_{i}}}$ .
Zmienna modelowa jest wyznaczona jednoznacznie (niezależnie od wyboru ciągów liniowo niezależnych)

$\widehat{Y}=\widetilde{X}\widetilde{B}_{{min}},$

gdzie

$\widetilde{B}_{{min}}=(\widetilde{X}^{T}\widetilde{X})^{{-1}}\widetilde{X}^{T}Y.$

Natomiast $SKR$ przyjmuje minimum na podprzestrzeni afinicznej złożonej z punktów postaci

$B=B^{\ast}+b,$

gdzie

$B^{\ast}_{j}=\left\{\begin{array}[]{ccc}\widetilde{B}_{{min,{i}}}&\mbox{gdy}&j=j_{i},\\ 0&\mbox{gdy}&j\not\in\{ j_{1},\dots,j_{k}\},\end{array}\right.$

a wektory $b$ opisują zależności między ciągami $X_{i}$

$b\in ker(X)=\{ v\in\mathbb{R}^{m}:Xv=0\}.$

Ponadto spełnione są punkty 1,2 i 3 z powyższego wniosku.

2.2. Odrobina algebry liniowej

Oznaczmy przez $\cal X$ podprzestrzeń liniową przestrzeni $\mathbb{R}^{n}$ rozpiętą przez kolumny macierzy $X$ ,

${\cal X}=lin(X_{1},\dots,X_{m})=\{ XV:V\in\mathbb{R}^{m}\}.$

Lemat 2.1

Macierz kwadratowa $n\times n$

$P=X(X^{T}X)^{{-1}}X^{T}$

jest macierzą rzutu prostopadłego na podprzestrzeń $\cal X$ , a macierz

$M=Id_{n}-P$

macierzą rzutu prostokątnego na podprzestrzeń ${\cal X}^{\perp}$ (dopełnienie ortogonalne $\cal X$ ).

Dowód.
Mnożenie przez macierz $P$ zachowuje wektory z $\cal X$

$P(XV)=X(X^{T}X)^{{-1}}X^{T}XV=X((X^{T}X)^{{-1}}X^{T}X)V=XV$

i anihiluje wektory prostopadłe do $\cal X$

$X^{T}W=0\Rightarrow PW=X(X^{T}X)^{{-1}}X^{T}W=X(X^{T}X)^{{-1}}(X^{T}W)=0.$

Natomiast mnożenie przez macierz $M$ anihiluje wektory z $\cal X$ i zachowuje wektory prostopadłe do $\cal X$

$M(XV)=XV-(PX)V=XV-XV=0,\;\;\; MW=W-PW=W.$

$\Box$

Lemat 2.2

1. Macierze $P$ i $M$ są symetryczne i idempotentne

$P^{T}=P,\;\;\; M^{T}=M,\;\;\; PP=P,\;\;\; MM=M.$

2. Rząd macierzy $P$ wynosi $m$ , a $M$ $n-m$ .

$rk\, P=m,\;\;\; rk\, M=n-m.$

3. Ślad macierzy $P$ wynosi $m$ , a $M$ $n-m$ .

$tr\, P=m,\;\;\; tr\, M=n-m.$

4. Istnieje taka $n\times n$ macierz unitarna $U$ (tzn. $U^{T}U=Id$ ), że macierze $U^{T}PU$ i $U^{T}MU$ są diagonalne o wyrazach 0 lub 1. $U^{T}PU$ ma na przekątnej $m$ jedynek, a $U^{T}MU$ $n-m$ .

Dowód.
Ad.1. $P$ i $M$ są macierzami rzutów zatem $PP=P$ i $MM=M$ . Symetria wynika z faktu, że transpozycja jest przemienna z odwracaniem macierzy

$P^{T}=(X(X^{T}X)^{{-1}}X^{T})^{T}=X((X^{T}X)^{T})^{{-1}}X^{T}=X(X^{T}X)^{{-1}}X^{T}=P,$

$M^{T}=(Id-P)^{T}=Id^{T}-P^{T}=Id-P=M.$

Ad.2. Rząd macierzy jest równy wymiarowi obrazu, zatem

$rk\, P=dim\,{\cal X}=rk\, X=m,$

$rk\, M=dim\,{\cal X}^{\perp}=n-m.$

Ad.3. $P$ jest macierzą rzutu na podprzestrzeń $m$ wymiarową, a zatem ma $m$ wartości własnych równych 1 i $n-m$ równych 0. Natomiast $M$ jest macierzą rzutu na podprzestrzeń $n-m$ wymiarową, a zatem ma $n-m$ wartości własnych równych 1 i $m$ równych 0. Ponieważ ślad jest to suma wartości własnych to wynosi on odpowiednio $m$ i $n-m$ .
Ad.4. Niech wektory $U_{1},\dots,U_{m}$ tworzą bazę ortonormalną podprzestrzeni ${\cal X}$ , a $U_{{m+1}},\dots U_{n}$ bazę podprzestrzeni ${\cal X}^{\perp}$ . Niech $U$ będzie macierzą o kolumnach $U_{i}$ . Wówczas