Zagadnienia

6.1 Funkcja Cobba-Douglasa
6.2 Przykład Nerlove'a

6. Modele produkcji - funkcja Cobba-Douglasa

Klasyczny jednorównaniowy liniowy model ekonometryczny -cd. Przykład: Modele produkcji - funkcja Cobba-Douglasa. (1 wykład)

6.1. Funkcja Cobba-Douglasa

6.1.1. Wprowadzenie

Funkcja Cobba-Douglasa to funkcyjne przedstawienie zależności wielkości produkcji $Q$ od nakładów na czynniki produkcji. W dalszym ciągu ograniczymy sie do trzech czynników pracy $x_{1}$ , kapitału $x_{2}$ i paliwa $x_{3}$ .

$Q=Ax_{1}^{{\alpha _{1}}}x_{2}^{{\alpha _{2}}}x_{3}^{{\alpha _{3}}},\;\;\; 0<\alpha _{i}<1,\;\;\; x_{i}>0.$

Współczynnik $A$ zależy od efektywności konkretnej firmy.

Funkcja Cobba-Douglasa jest chętnie wykorzystywana w modelowaniu, gdyż dobrze przedstawia następujące fakty stylizowane:
$\bullet$ monotoniczność;
$Q$ jest rosnąca ze względu na każdy $x_{i}$ ,

$\frac{\partial Q}{\partial x_{i}}=\alpha _{i}\frac{Q}{x_{i}}>0.$

$\bullet$ wklęsłość;
$Q$ jest wklęsła ze względu na każdy $x_{i}$ ,

$\frac{\partial^{2}Q}{\partial x_{i}^{2}}=\alpha _{i}(\alpha _{i}-1)\frac{Q}{x_{i}^{2}}<0.$

Funkcja zachowuje zasadę malejących przychodów – każda kolejna jednostka jednego z zasobów bez wzrostu zasobu drugiego skutkuje mniejszym przyrostem produkcji.
$\bullet$ wzrost przychodów przy zwiększaniu nakładów na dwa czynniki produkcji;

$\frac{\partial^{2}Q}{\partial x_{i}\partial x_{j}}=\alpha _{i}\alpha _{j}\frac{Q}{x_{i}x_{j}}>0\;\;\;\mbox{ dla }\;\; i\neq j.$

$\bullet$ stała elastyczność ze względu na każdy czynnik produkcji;

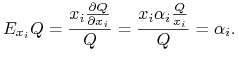$E_{{x_{i}}}Q=\frac{x_{i}\frac{\partial Q}{\partial x_{i}}}{Q}=\frac{x_{i}\alpha _{i}\frac{Q}{x_{i}}}{Q}=\alpha _{i}.$

Uwaga 6.1

Elastyczność mówi nam o ile wzrośnie produkcja gdy zwiększymy nakłady na czynnik produkcji

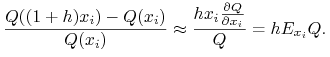$\frac{Q((1+h)x_{i})-Q(x_{i})}{Q(x_{i})}\approx\frac{hx_{i}\frac{\partial Q}{\partial x_{i}}}{Q}=hE_{{x_{i}}}Q.$

6.1.2. Efekt skali

Zmniejszamy albo zwiększamy proporcjonalnie wszystkie $x_{i}$

$x_{i}^{\prime}=hx_{i},\;\;\; h>0,\;\;\; i=1,2,3.$

Wówczas nowa wielkość produkcji wyniesie:

$Q^{\prime}=Q(x^{\prime})=Ax_{1}^{{\alpha _{1}}}x_{2}^{{\alpha _{2}}}x_{3}^{{\alpha _{3}}}h^{{\alpha _{1}+\alpha _{2}+\alpha _{3}}}.$

Czyli

$\frac{Q^{\prime}}{Q}=h^{{\alpha _{1}+\alpha _{2}+\alpha _{3}}}.$

Zauważmy, że gdy $\alpha _{1}+\alpha _{2}+\alpha _{3}>1$ to

$h>1\Rightarrow\frac{Q^{\prime}}{Q}>h,$

$h<1\Rightarrow\frac{Q^{\prime}}{Q}<h.$

Wniosek: opłaca się zwiększyć nakłady i produkcję.

Gdy $\alpha _{1}+\alpha _{2}+\alpha _{3}<1$ to

$h>1\Rightarrow\frac{Q^{\prime}}{Q}<h,$

$h<1\Rightarrow\frac{Q^{\prime}}{Q}>h.$

Wniosek: opłaca się zmniejszyć nakłady i produkcję.

Podsumowując, jeśli obserwujemy ,,stan równowagi” to $\alpha _{1}+\alpha _{2}+\alpha _{3}=1$ . Mówimy wówczas o braku efektów skali.

6.1.3. Koszty produkcji

Koszty całkowite produkcji $TC$ można wyrazić za pomocą kosztów jednostkowych dla poszczególnych czynników produkcji

$TC=p_{1}x_{1}+p_{2}x_{2}+p_{3}x_{3}.$

Zadanie: Zminimalizować koszty dla zadanego poziomu produkcji $Q$ , $Q>0$ .

$TC(x)\longrightarrow min,\;\; Q(x)=Q.$

Lemat 6.1

Powyższe zadanie optymalizacyjne posiada dokladnie jedno rozwiązanie.

$TC_{{min}}=\frac{r}{\left(A\alpha _{1}^{{\alpha _{1}}}\alpha _{2}^{{\alpha _{2}}}\alpha _{3}^{{\alpha _{3}}}\right)^{{\frac{1}{r}}}}Q^{{\frac{1}{r}}}p_{1}^{{\frac{\alpha _{1}}{r}}}p_{2}^{{\frac{\alpha _{2}}{r}}}p_{3}^{{\frac{\alpha _{3}}{r}}},$

gdzie $r=\alpha _{1}+\alpha _{2}+\alpha _{3}$ .

Dowód. Połóżmy,

$\widetilde{x}_{i}=Q^{{\frac{1}{r}}}A^{{-\frac{1}{r}}},\;\;\; i=1,2,3.$

Jak łatwo zauważyć

$Q(\widetilde{x})=Q.$

Połóżmy

$T=TC(\widetilde{x}).$

Ponieważ zbiór

$M=\{ x\in\mathbb{R}^{3}:x_{i}\geq 0,\;\; TC(x)\leq T,\;\;\; Q(x)=Q\},$

jest niepusty, domknięty i ograniczony, zatem badane zadanie optymalizacyjne posiada rozwiązanie.

Rozważmy warunek konieczny istnienia lokalnego ekstremum – $\nabla Q\parallel\nabla TC$ .

$\nabla Q=Q(x)\left(\frac{\alpha _{1}}{x_{1}},\frac{\alpha _{2}}{x_{2}},\frac{\alpha _{3}}{x_{3}}\right),\;\;\;\nabla TC=(p_{1},p_{2},p_{3}).$

Równoległość gradientów implikuje istnienie stałej $\lambda$ takiej, że

$\frac{\alpha _{1}}{p_{1}x_{1}}=\frac{\alpha _{2}}{p_{2}x_{2}}=\frac{\alpha _{3}}{p_{3}x_{3}}=\lambda.$

A zatem

$x_{i}=\frac{\alpha _{i}}{\lambda p_{i}},\;\;\; i=1,2,3.$

Po podstawieniu do warunku $Q(x)=Q$ otrzymujemy

$Q=A\left(\frac{\alpha _{1}}{\lambda p_{1}}\right)^{{\alpha _{1}}}\left(\frac{\alpha _{2}}{\lambda p_{2}}\right)^{{\alpha _{2}}}\left(\frac{\alpha _{3}}{\lambda p_{3}}\right)^{{\alpha _{3}}}=\lambda^{{-r}}A\alpha _{1}^{{\alpha _{1}}}\alpha _{2}^{{\alpha _{2}}}\alpha _{3}^{{\alpha _{3}}}p_{1}^{{-\alpha _{1}}}p_{2}^{{-\alpha _{2}}}p_{3}^{{-\alpha _{3}}},$

gdzie $r=\alpha _{1}+\alpha _{2}+\alpha _{3}$ . Wyznaczamy $\lambda$

$\lambda=Q^{{-\frac{1}{r}}}\left(A\alpha _{1}^{{\alpha _{1}}}\alpha _{2}^{{\alpha _{2}}}\alpha _{3}^{{\alpha _{3}}}\right)^{{\frac{1}{r}}}p_{1}^{{-\frac{\alpha _{1}}{r}}}p_{2}^{{-\frac{\alpha _{2}}{r}}}p_{3}^{{-\frac{\alpha _{3}}{r}}}.$

Teraz możemy wyznaczyć $TC_{{min}}$

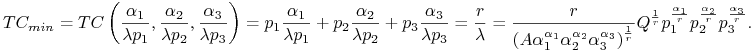$TC_{{min}}=TC\left(\frac{\alpha _{1}}{\lambda p_{1}},\frac{\alpha _{2}}{\lambda p_{2}},\frac{\alpha _{3}}{\lambda p_{3}}\right)=p_{1}\frac{\alpha _{1}}{\lambda p_{1}}+p_{2}\frac{\alpha _{2}}{\lambda p_{2}}+p_{3}\frac{\alpha _{3}}{\lambda p_{3}}=\frac{r}{\lambda}=\frac{r}{\left(A\alpha _{1}^{{\alpha _{1}}}\alpha _{2}^{{\alpha _{2}}}\alpha _{3}^{{\alpha _{3}}}\right)^{{\frac{1}{r}}}}Q^{{\frac{1}{r}}}p_{1}^{{\frac{\alpha _{1}}{r}}}p_{2}^{{\frac{\alpha _{2}}{r}}}p_{3}^{{\frac{\alpha _{3}}{r}}}.$

$\Box$

6.2. Przykład Nerlove'a

6.2.1. Charakterystyka danych

M.Nerlove przeprowadził badania dotyczące produkcji energii elektrycznej w USA w 1955 roku. Dane zostały zebrane dla 145 spółek w 44 stanach. Dotyczą one:
$\bullet$ całkowitych kosztów $TC$ (mln USD),
$\bullet$ wielkości produkcji $Q$ (mld kWh),
$\bullet$ średnich zarobków (koszt pracy) $PL=p_{1}$ ,
$\bullet$ ceny kapitału (stopy procentowe) $PK=p_{2}$ ,
$\bullet$ ceny paliwa $PF=p_{3}$ .

Warunki działania spółek:
$\bullet$ dostawa energii zgodnie z zapotrzebowaniem,
$\bullet$ cena energii ustalana administracyjnie dla regionu,
$\bullet$ firmy nie mają bezpośredniego wpływu na $PL$ , $PK$ i $PF$ . $PF$ i $PK$ kształtuje rynek, a $PL$ długoterminowe umowy ze związkami zawodowymi.

6.2.2. Konstrukcja modelu

Model ekonometryczny:

$TC_{i}=e^{{\mu _{i}}}Q_{i}^{{\beta _{2}}}p_{{i,1}}^{{\beta _{3}}}p_{{i,2}}^{{\beta _{4}}}p_{{i,3}}^{{\beta _{5}}},\;\;\;\beta _{2}=\frac{1}{r},\;\;\;\beta _{{2+j}}=\frac{\alpha _{j}}{r},\;\;\; j=1,2,3.$

(6.1)

$\mu _{i}=\ln\left(r\left(A_{i}\alpha _{1}^{{\alpha _{1}}}\alpha _{2}^{{\alpha _{2}}}\alpha _{3}^{{\alpha _{3}}}\right)^{{-\frac{1}{r}}}\right).$

$\mu _{i}$ zawiera część losową zależną od firmy,

$E(\mu _{i})=\beta _{1},\;\;\;\mu _{i}=\beta _{1}+\varepsilon _{i}.$

Logarytmujemy równanie 6.1 i przechodzimy do modelu liniowego

$\ln TC_{i}=\beta _{1}+{\beta _{2}}\ln Q_{i}+{\beta _{3}}\ln p_{{i,1}}+{\beta _{4}}\ln p_{{i,2}}+{\beta _{5}}\ln p_{{i,3}}+\varepsilon _{i}.$

(6.2)

Dodatkowo rozważamy model ograniczony, w którym spełniona jest zależność $\beta _{3}+\beta _{4}+\beta _{5}=1$ . Podstawiamy $\beta _{5}=1-\beta _{3}-\beta _{4}$ i otrzymujemy

$\ln\left(\frac{TC_{i}}{p_{{i,3}}}\right)=\beta _{1}+{\beta _{2}}\ln Q_{i}+{\beta _{3}}\ln\frac{p_{{i,1}}}{p_{{i,3}}}+{\beta _{4}}\ln\frac{p_{{i,2}}}{p_{{i,3}}}+\varepsilon _{i}.$

(6.3)

6.2.3. Estymacja parametrów modelu 6.2

Estymujemy parametry strukturalne metodą MNK. Otrzymujemy następujące równanie regresji. W nawiasach podane są odchylenia standardowe estymatorów.

$\begin{array}[]{llllll}\ln TC=&-3{,}5&+0{,}72\ln Q&+0{,}44\ln p_{1}&-0{,}22\ln p_{2}&+0{,}43\ln p_{3}\\ &(1{,}8)&(0{,}017)&(0{,}29)&(0{,}34)&(0{,}10)\end{array}$

Ponadto suma kwadratów składnika resztowego wyniosła $SKR=21{,}552$ .
Uwaga: Test $t$ wskazuje na statystyczną nieistotność parametru $\beta _{4}$ .

6.2.4. Estymacja parametrów modelu 6.3

Estymujemy parametry strukturalne metodą MNK. Otrzymujemy następujące równanie regresji. W nawiasach podane są odchylenia standardowe estymatorów.

$\begin{array}[]{lllll}\ln\frac{TC}{p_{3}}=&-4{,}7&+0{,}72\ln Q&+0{,}59\ln\frac{p_{1}}{p_{3}}&-0{,}007\ln\frac{p_{2}}{p_{3}}\\ &(0{,}88)&(0{,}017)&(0{,}20)&(0{,}19)\end{array}$

Ponadto suma kwadratów składnika resztowego wyniosła $SKR_{o}=21{,}640$ .
Uwaga: Test $t$ wskazuje na statystyczną nieistotność parametru $\beta _{4}$ .

6.2.5. Test jednorodności modelu

Testujemy hipotezę $H_{0}:\beta _{3}+\beta _{4}+\beta _{5}=1$ wobec $H_{1}:\beta _{3}+\beta _{4}+\beta _{5}\neq 1$ na poziomie istotności $\alpha=0{,}05$ .
Mamy $m=1$ , $n-K=145-5=140$ stopni swobody. Wyznaczamy statystykę $F$ .

$F=\frac{SKR_{o}-SKR}{SKR}\cdot\frac{n-K}{m}=0{,}57.$

Wartość krytyczną $F^{\ast}$ wyznaczamy z rozkładu Snedecora $F(1,140)$ otrzymujemy

$F^{\ast}=3{,}9\gg F.$

Zatem nie ma podstaw do odrzucenia hipotezy $H_{0}$ .

6.2.6. Test braku efektów skali dla modelu ograniczonego 6.3

Testujemy hipotezę $H_{0}:\beta _{2}=1$ wobec $H_{1}:\beta _{2}\neq 1$ na poziomie istotności $\alpha=0{,}05$ .
Mamy $n-K=145-4=141$ stopni swobody. Wyznaczamy statystykę $t$