« 7. Modele nieliniowe  Spis treści  9. Teoria dużej próbki »  

Zagadnienia

8. Metody asymptotyczne

Zbieżność ciągów zmiennych losowych. Metoda delty. Asymptotyczna normalność estymatorów. Stacjonarność i ergodyczność. Ciągi przyrostów martyngałowych. Centralne Twierdzenie Graniczne dla przyrostów martyngałowych. (1 wykład)

8.1. Zbieżność zmiennych losowych

Omówimy pokrótce trzy pojęcia zbieżności zmiennych losowych.
Niech (\Omega,{\cal M},P) – przestrzeń probabilistyczna. Rozważmy ciąg zmiennych losowych (Z_{n})_{{n=0}}^{\infty} o wartościach w \mathbb{R}^{K}.

Definicja 8.1

Ciąg zmiennych losowych Z_{n} zbiega prawie napewno do zmiennej losowej Z gdy

P(\lim _{{n\rightarrow\infty}}Z_{n}=Z)=1.

W zapisie skróconym będziemy pisali

Z_{n}\stackrel{as}{\longrightarrow}Z\;\;\;\mbox{ lub }\;\;\; Z_{n}\stackrel{pn}{\longrightarrow}Z.
Definicja 8.2

Ciąg zmiennych losowych Z_{n} zbiega według prawdopodobieństwa do zmiennej losowej Z gdy

\forall\varepsilon>0\;\;\lim _{{n\rightarrow\infty}}P(\| Z_{n}-Z\|>\varepsilon)=0,

gdzie \|\cdot\| oznacza normę w \mathbb{R}^{K}.

W zapisie skróconym będziemy pisali

\mathop{\mathrm{plim}}\displaylimits _{{n\rightarrow\infty}}Z_{n}=Z\;\;\;\mbox{ lub }\;\;\; Z_{n}\stackrel{p}{\longrightarrow}Z.
Definicja 8.3

Ciąg zmiennych losowych Z_{n} zbiega według rozkładu do zmiennej losowej Z gdy ciąg dystrybuant F_{{Z_{n}}} zbiega do dystrybuanty F_{Z} w każdym punkcie ciągłości F_{Z}.

W zapisie skróconym będziemy pisali

Z_{n}\stackrel{d}{\longrightarrow}Z\;\;\;\mbox{ lub }\;\;\; Z_{n}\stackrel{d}{\longrightarrow}{\cal R},

gdzie R jest rozkładem zmiennej losowej Z.

Uwaga 8.1

Jeśli ciąg różnic Z_{n}-Y_{n} zbiega do 0 według prawdopodobieństwa i ciąg Z_{n} zbiega według rozkładu do zmiennej losowej Z, to również Y_{n} zbiega według rozkładu do Z

Z_{n}\stackrel{d}{\longrightarrow}Z,\;\;\; Z_{n}-Y_{n}\stackrel{p}{\longrightarrow}0\;\;\;\Longrightarrow\;\;\; Y_{n}\stackrel{d}{\longrightarrow}Z.
Uwaga 8.2

Trzy powyższe zbieżności są od siebie zależne. Mamy

Z_{n}\stackrel{as}{\longrightarrow}Z\;\;\Longrightarrow\;\; Z_{n}\stackrel{p}{\longrightarrow}Z\;\;\Longrightarrow\;\; Z_{n}\stackrel{d}{\longrightarrow}Z.

Aby zamknąć powyższy diagram należy dopuścić zmianę przestrzeni probabilistycznej i skorzystać z następującego twierdzenia o reprezentacji prawie napewno.

Twierdzenie 8.1

(Skorochod)
Jeśli ciąg zmiennych losowych Z_{n} zbiega według rozkładu do zmiennej losowej Z to istnieje przestrzeń probabilistyczna (\Omega^{\prime},{\cal M}^{\prime},P^{\prime}) i określone na niej zmienne losowe Y i Y_{n}, n=0,1,\dots takie, że Y ma ten sam rozkład co Z, a Y_{n} co Z_{n} i ciąg zmiennych losowych Y_{n} zbiega prawie napewno do zmiennej losowej Y.

Sformułujemy teraz kilka przydatnych w ekonometrii twierdzeń o zbieżności zmiennych losowych.

Twierdzenie 8.2

O odwzorowaniu ciągłym.[2, 16]
Niech D_{f} oznacza zbiór punktów nieciągłości funkcji

f:\mathbb{R}^{k}\rightarrow\mathbb{R}^{m}.

Wówczas jeśli ciąg zmiennych losowych Z_{n} zbiega według rozkładu, prawdopodobieństwa lub prawie napewno do zmiennej losowej Z takiej, że

P(Z\in D_{f})=0,

to ciąg zmiennych losowych f(Z_{n}) zbiega odpowiednio według rozkładu, prawdopodobieństwa lub prawie napewno do zmiennej losowej f(Z).

Twierdzenie 8.3

(Slutsky)
Niech (X_{n}) i (Y_{n}) ciagi zmiennych losowych o wartościach macierzowych, X macierzowa zmienna losowa i C macierz (deterministyczna). Wówczas, jeśli

X_{n}\stackrel{d}{\longrightarrow}X,\;\;\;\mbox{ a }\;\; Y_{n}\stackrel{d}{\longrightarrow}C,

to:

\displaystyle a. \displaystyle X_{n}+Y_{n}\stackrel{d}{\longrightarrow}X+C,
\displaystyle b. \displaystyle Y_{n}X_{n}\stackrel{d}{\longrightarrow}CX,
\displaystyle c. \displaystyle\exists C^{{-1}}\;\;\;\Longrightarrow\;\;\; Y_{n}^{{-1}}X_{n}\stackrel{d}{\longrightarrow}C^{{-1}}X,

gdzie Y_{n}^{{-1}} to dowolna macierz losowa taka, że

Y_{n}(\omega)Y_{n}^{{-1}}(\omega)=Id

gdy \det Y_{n}(\omega)\neq 0.

Dowód.
Ponieważ Y_{n} zbiega do stałej, to

(X_{n},Y_{n})\stackrel{d}{\longrightarrow}(X,C).

Działania +,\cdot są ciągłe zatem z twierdzenia o odwzorowaniu ciągłym (8.2) otrzymujemy tezę twierdzenia.
W przypadku odwracania macierzy zbiorem punktów nieciągłości jest zbiór macierzy o wyznaczniku 0. Zatem wystarczy zauważyć, że prawdopodobieństwo, że odwracalna macierz deterministyczna ma zerowy wyznacznik jest równe 0.

\Box
Uwaga 8.3

Niech X_{n}i X to wektory kolumnowe, czyli macierze K\times 1, a Y_{n} i C macierze K\times K. Wówczas, jeśli

X_{n}\stackrel{d}{\longrightarrow}N(0,\Sigma),\;\;\; Y_{n}\stackrel{d}{\longrightarrow}C,

to

Y_{n}X_{n}\stackrel{d}{\longrightarrow}N(0,C\Sigma C^{T}).
Twierdzenie 8.4

Metoda delty.
Niech X_{n} ciąg zmiennych losowych o wartościach w \mathbb{R}^{m}, X zmienna losowa o wartościach w \mathbb{R}^{m}, C punkt z \mathbb{R}^{m}, a f:\mathbb{R}^{m}\rightarrow\mathbb{R}^{K} funkcja różniczkowalna w C. Wówczas, jeśli

X_{n}\stackrel{d}{\longrightarrow}C,\;\;\;\mbox{ i }\;\;\;\sqrt{n}(X_{n}-C)\stackrel{d}{\longrightarrow}X

to

\sqrt{n}(f(X_{n})-f(C))\stackrel{d}{\longrightarrow}Df(C)X.

Dowód.
Korzystając z twierdzenia 8.1 o reprezentacji prawie napewno, możemy zastąpić ciąg X_{n} ciągiem X_{n}^{\prime}\; takim, że

X_{n}^{\prime}\stackrel{d}{\sim}X_{n},\;\;\; X_{n}^{\prime}\stackrel{as}{\longrightarrow}C,\;\;\;\mbox{ i }\;\;\;\sqrt{n}(X_{n}^{\prime}-C)\stackrel{d}{\longrightarrow}X.

Wówczas

\sqrt{n}(f(X_{n})-f(C))\stackrel{d}{\sim}\sqrt{n}(f(X_{n}^{\prime})-f(C))=
=\sqrt{n}(f(X_{n}^{\prime})-f(C)-Df(C)(X_{n}^{\prime}-C))+\sqrt{n}Df(C)(X_{n}^{\prime}-C)=
=\frac{f(X_{n}^{\prime})-f(C)-Df(C)(X_{n}^{\prime}-C)}{\| X_{n}^{\prime}-C\|}\sqrt{n}\| X_{n}^{\prime}-C\|+DF(C)(\sqrt{n}(X_{n}^{\prime}-C)).

Z różniczkowalności f otrzymujemy

\frac{f(X_{n}^{\prime})-f(C)-Df(C)(X_{n}^{\prime}-C)}{\| X_{n}^{\prime}-C\|}\stackrel{as}{\longrightarrow}0.

Ponieważ

\sqrt{n}\| X_{n}^{\prime}-C\|\stackrel{d}{\longrightarrow}\| X\|\;\;\;\mbox{i }\;\;\; DF(C)(\sqrt{n}(X_{n}^{\prime}-C))\stackrel{d}{\longrightarrow}Df(C)X,

to z twierdzenia Slutsky'ego (8.3) otrzymujemy

\sqrt{n}(f(X_{n})-f(C))\stackrel{d}{\longrightarrow}0\| X\|+Df(C)X.
\Box
Uwaga 8.4

Jeśli przy założeniach twierdzenia 8.4 X ma rozkład normalny N(0,\Sigma) to

\sqrt{n}(f(X_{n})-f(C))\stackrel{d}{\longrightarrow}N(0,Df(C)\,\Sigma Df(C){}^{T}).

8.2. Estymatory jako ciągi zmiennych losowych

Załóżmy, że proces generujący dane Z_{t}, t=0,1,\dots, pochodzi z parametrycznej rodziny procesów {\cal SP}(\theta), gdzie zbiór parametrów \Theta jest podzbiorem \mathbb{R}^{m}

\theta\in\Theta\subset\mathbb{R}^{m}.

Ustalmy funkcję \nu:\Theta\longrightarrow\mathbb{R}^{k} i rodzinę estymatorów

\widehat{\nu}=\left(\widehat{\nu}_{n}\right)_{{n=1}}^{{\infty}},

wartości funkcji \nu w punkcie \theta _{Z}. Niech \widehat{\nu}_{n} będzie estymatorem \nu(\theta _{Z}), wyznaczonym na podstawie próbki rozmiaru n, tzn.

\widehat{\nu}_{n}=\widehat{\nu}_{n}(Z_{0},\dots,Z_{{n-1}}).
Definicja 8.4

Ciąg estymatorów \widehat{\nu} nazywamy nazywamy zgodnym gdy

\mathop{\mathrm{plim}}\displaylimits _{{n\rightarrow\infty}}\widehat{\nu}_{n}=\nu(\theta _{Z}).
Definicja 8.5

Zgodny ciąg estymatorów \widehat{\nu} nazywamy nazywamy asymptotycznie normalnym gdy

\sqrt{n}(\widehat{\nu}_{n}-\nu(\theta _{Z}))\stackrel{d}{\longrightarrow}N(0,\Sigma).
Uwaga 8.5

Macierz \Sigma oznaczamy Avar(\widehat{\nu}) i nazywamy asymptotyczną wariancją estymatora \widehat{\nu}_{n}.

8.3. Stacjonarność i ergodyczność procesów stochastycznych

8.3.1. Definicje i podstawowe własności

Niech Z=(Z_{t})_{{t=0}}^{{\infty}} będzie K-wymiarowym procesem stochastycznym (ciągiem zmiennych losowych) określonym na przestrzeni probabilistycznej (\Omega,{\cal M},P).

Definicja 8.6

Proces stochastyczny Z jest (silnie) stacjonarny gdy dla dowolnych p,q,r\in\mathbb{N} łączne rozkłady

\{ Z_{p},Z_{{p+1}},\dots,Z_{{p+q}}\}\;\;\;\mbox{ i }\;\;\;\{ Z_{{r}},\dots,Z_{{r+q}}\}

są identyczne.

Wniosek 8.1

Jeśli proces stochastyczny Z jest stacjonarny i Z_{t} należą do L^{2}, to dla wszystkich p,q,r\in\mathbb{N}

E(Z_{p})=E(Z_{{r}}),\;\;\; Cov(Z_{p},Z_{{p+q}})=Cov(Z_{r},Z_{{r+q}}).
Definicja 8.7

Stacjonarny proces stochastyczny Z ma własność mieszania gdy dla dowolnych ograniczonych funkcji borelowskich f i g oraz indeksów p,l,m\in\mathbb{N}

\lim _{{n\rightarrow\infty}}E(f(Z_{p},\dots,Z_{{p+m}})g(Z_{n},\dots,Z_{{n+l}}))=E(f(Z_{p},\dots,Z_{{p+m}}))E(g(Z_{p},\dots,Z_{{p+l}})).
Definicja 8.8

Stacjonarny proces stochastyczny Z jest ergodyczny gdy

\forall A\in{\cal B}(R^{K})\;\;\; P(\forall t\;\; Z_{t}\in A)\in\{ 0,1\}.
Twierdzenie 8.5

Twierdzenie ergodyczne.
Jeśli proces stochastyczny Z jest stacjonarny i Z_{t} należą do L^{1}, to zachodzdzą implikacje

a\Longrightarrow b\Longrightarrow c,

gdzie
a. Z ma własność mieszania,
b. Z jest ergodyczny,
c. średnie zbiegają do wartości oczekiwanej

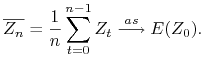\overline{Z_{n}}=\frac{1}{n}\sum _{{t=0}}^{{n-1}}Z_{t}\stackrel{as}{\longrightarrow}E(Z_{0}).
Uwaga 8.6

Jeśli proces stochastyczny Z jest stacjonarny i ma własność mieszania a f jest funkcją borelowską to proces Z^{\prime}=(f(Z_{t},\dots,Z_{{t+q}}))_{{t=0}}^{{\infty}} też jest stacjonarny i ma własność mieszania.
Zatem jeśli Z_{t} należą do L^{2} to

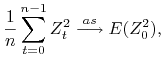\frac{1}{n}\sum _{{t=0}}^{{n-1}}Z_{t}^{2}\stackrel{as}{\longrightarrow}E(Z_{0}^{2}),
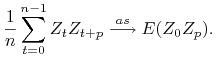\frac{1}{n}\sum _{{t=0}}^{{n-1}}Z_{t}Z_{{t+p}}\stackrel{as}{\longrightarrow}E(Z_{0}Z_{p}).
Wniosek 8.2

Dla procesów stacjonarnych i ergodycznych średnie próbkowe są zgodnymi estymatorami.

8.3.2. Przykłady

Definicja 8.9

Proces \varepsilon nazywamy gaussowskim białym szumem gdy

\varepsilon=(\varepsilon _{t})_{{t=0}}^{{\infty}},\;\;\;\varepsilon _{t}\sim N(0,\sigma),\;\;\sigma>0,\;\;\;\varepsilon _{t}\mbox{ niezależne}.
Lemat 8.1

Biały szum jest stacjonarny i ergodyczny.

Dowód.
Dla dowolnych indeksów p i q wektor (\varepsilon _{p},\dots,\varepsilon _{{p+q}}) ma rozkład N(0,Id_{{q+1}}). Rozkład ten nie zależy od p co implikuje stacjonarność.

Aby pokazać własność mieszania zauważmy, że dla n>p+m zmienne losowe f(\varepsilon _{p},\dots,\varepsilon _{{p+m}}) i g(\varepsilon _{n},\dots,\varepsilon _{{n+l}}) są niezależne. Zatem dla n odpowiednio dużych

E(f(\varepsilon _{p},\dots,\varepsilon _{{p+m}})g(\varepsilon _{n},\dots,\varepsilon _{{n+l}}))=E(f(\varepsilon _{p},\dots,\varepsilon _{{p+m}}))E(g(\varepsilon _{n},\dots,\varepsilon _{{n+l}}))=
=E(f(\varepsilon _{p},\dots,\varepsilon _{{p+m}}))E(g(\varepsilon _{p},\dots,\varepsilon _{{p+l}})).
\Box
Uwaga 8.7

Powyższe rozumowanie można zastosować dla dowolnego procesu iid tzn. o wyrazach niezależnych i o jednakowym rozkładzie.

Proces autoregresyjny

Niech \varepsilon będzie gaussowskim białym szumem. Dodatkowo założymy, ze \varepsilon _{t}\sim N(0,1). Proces Z=(Z_{t}) zdefiniujemy rekurencyjnie:

Z_{t}=c+\rho Z_{{t-1}}+\sigma\varepsilon _{t},\;\;\; t=1,2,\dots,
Z_{0}=\frac{c}{1-\rho}+\frac{\sigma}{\sqrt{1-\rho^{2}}}\varepsilon _{0},

gdzie c,\rho,\sigma rzeczywiste parametry, |\rho|<1, \sigma>0. Tak zdefiniowany proces nazywa się autoregresyjnym rzędu 1 (AR(1)).

Lemat 8.2

Proces Z jest stacjonarny i ergodyczny.

Dowód.

Krok 1. Pokażemy, że wszystkie Z_{t} mają rozkład normalny o parametrach \frac{c}{1-\rho} i \frac{\sigma^{2}}{1-\rho^{2}}

Z_{t}\sim N\left(\frac{c}{1-\rho},\frac{\sigma^{2}}{1-\rho^{2}}\right).

Zastosujemy indukcję po t.
Jak łatwo zauważyć Z_{0} ma rozkład normalny oraz

E(Z_{0})=\frac{c}{1-\rho},\;\;\; D^{2}(Z_{0})=\frac{\sigma^{2}}{1-\rho^{2}}.

Załóżmy, że

Z_{s}\sim N\left(\frac{c}{1-\rho},\frac{\sigma^{2}}{1-\rho^{2}}\right),\;\;\; s<t.

Ponieważ \varepsilon _{t} i Z_{{t-1}} mają rozkłady normalne i są niezależne to Z_{t} ma rozkład normalny. Ponadto

E(Z_{t})=c+\rho E(Z_{{t-1}})+\sigma E(\varepsilon)=c+\rho\frac{c}{1-\rho}+0=\frac{c}{1-\rho}.
D^{2}(Z_{t})=\rho^{2}D^{2}(Z_{{t-1}})+\sigma^{2}D^{2}(\varepsilon _{t})=\rho^{2}\frac{\sigma^{2}}{1-\rho^{2}}+\sigma^{2}=\frac{\sigma^{2}}{1-\rho^{2}}.

Krok 2. Pokażemy, że Cov(Z_{{t+k}},Z_{t})=\rho^{k}\frac{\sigma^{2}}{1-\rho^{2}}.
Zastosujemy indukcję po k.
Dla k=0 mamy

Cov(Z_{t},Z_{t})=D^{2}(Z_{t})=\frac{\sigma^{2}}{1-\rho^{2}}.

Załóżmy, że

Cov(Z_{{t+k-1}},Z_{t})=\rho^{{k-1}}\frac{\sigma^{2}}{1-\rho^{2}}.

Wówczas

Cov(Z_{{t+k}},Z_{t})=Cov(c+\rho Z_{{t+k-1}}+\sigma\varepsilon _{t},Z_{t})=\rho Cov(Z_{{t+k-1}},Z_{t})=\rho\cdot\rho^{{k-1}}\frac{\sigma^{2}}{1-\rho^{2}}=\rho^{{k}}\frac{\sigma^{2}}{1-\rho^{2}}.

Krok 3. Stacjonarność.
Z poprzednich dwóch ”kroków” wynika, że rozkład wektora (Z_{t},\dots,Z_{{t+p}}) nie zależy od t. Rzeczywiście

(Z_{t},\dots,Z_{{t+p}})\sim N(\frac{c}{1-\rho}e,\frac{\sigma^{2}}{1-\rho^{2}}R_{p}),

gdzie e jest wektorem o p+1 współrzędnych, które są wszystkie równe 1, e=(1,\dots,1), a R_{p} jest macierzą p+1\times p+1 o wyrazach (R_{p})_{{i,j}}=\rho^{{|i-j|}}, czyli

R_{p}=\left(\begin{array}[]{ccccc}1&\rho&\rho^{2}&\dots&\rho^{{p}}\\ \rho&1&\rho&\dots&\rho^{{p-1}}\\ \dots&\dots&\dots&\dots&\dots\\ \rho^{{p-1}},&\rho^{{p-2}}&\rho^{{p-3}}&\dots&\rho\\ \rho^{p},&\rho^{{p-1}}&\rho^{{p-2}}&\dots&1\end{array}\right).

Krok 4. Ergodyczność.
Dla n>p+m wektor (Z_{p},\dots,Z_{{p+m}},Z_{n},\dots,Z_{{n+l}}) ma m+l+2-wymiarowy rozkład normalny

(Z_{p},\dots,Z_{{p+m}},Z_{n},\dots,Z_{{n+l}})\sim N(\frac{c}{1-\rho}e,\frac{\sigma^{2}}{1-\rho^{2}}C_{n}),

gdzie macierz C otrzymujemy z macierzy R_{{n+l+1-p}} przez wycięcie kolumn i wierszy od m+2-giego do n-1-ego.

C_{n}=\left(\begin{array}[]{cc}R_{m}&\rho^{{n-p-m}}A\\ \rho^{{n-p-m}}A^{T}&R_{l}\end{array}\right),

gdzie m+1\times l+1 macierz A nie zależy od n, A_{{i,j}}=\rho^{{m+j-i}}

A=\left(\begin{array}[]{ccccc}\rho^{{m}}&\rho^{{m+1}}&\rho^{{m+2}}&\dots&\rho^{{m+l}}\\ \rho^{{m-1}}&\rho^{{m}}&\rho^{{m+1}}&\dots&\rho^{{m+l-1}}\\ \dots&\dots&\dots&\dots&\dots\\ \rho^{{1}},&\rho^{{2}}&\rho^{{3}}&\dots&\rho^{{l+1}}\\ {1},&\rho^{{1}}&\rho^{{2}}&\dots&\rho^{{l}}\end{array}\right).

Zatem

\lim _{{n\rightarrow\infty}}C_{n}^{{-1}}=C_{{\infty}}^{{-1}}=\left(\begin{array}[]{cc}R_{m}^{{-1}}&0\\ 0&R_{l}^{{-1}}\end{array}\right).

W oparciu o powyższą granicę pokażemy własność mieszania.

E(f(Z_{p},\dots,Z_{{p+m}})g(Z_{n},\dots,Z_{{n+l}}))=
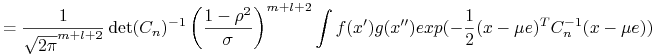=\frac{1}{\sqrt{2\pi}^{{m+l+2}}}\det(C_{n})^{{-1}}\left(\frac{1-\rho^{2}}{\sigma}\right)^{{m+l+2}}\int f(x^{\prime})g(x^{{\prime\prime}})exp(-\frac{1}{2}(x-\mu e)^{T}C_{n}^{{-1}}(x-\mu e))
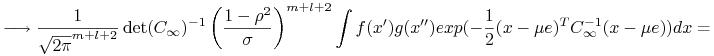\longrightarrow\frac{1}{\sqrt{2\pi}^{{m+l+2}}}\det(C_{{\infty}})^{{-1}}\left(\frac{1-\rho^{2}}{\sigma}\right)^{{m+l+2}}\int f(x^{\prime})g(x^{{\prime\prime}})exp(-\frac{1}{2}(x-\mu e)^{T}C_{{\infty}}^{{-1}}(x-\mu e))dx=
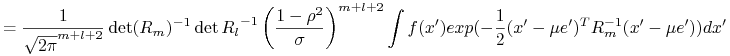=\frac{1}{\sqrt{2\pi}^{{m+l+2}}}\det(R_{m})^{{-1}}\det{R_{l}}^{{-1}}\left(\frac{1-\rho^{2}}{\sigma}\right)^{{m+l+2}}\int f(x^{\prime})exp(-\frac{1}{2}(x^{\prime}-\mu e^{\prime})^{T}R_{m}^{{-1}}(x^{\prime}-\mu e^{\prime}))dx^{\prime}
\int g(x^{{\prime\prime}})exp(-\frac{1}{2}(x^{{\prime\prime}}-\mu e^{{\prime\prime}})^{T}R_{l}^{{-1}}(x^{{\prime\prime}}-\mu e^{{\prime\prime}}))dx^{{\prime\prime}}=
=E(f(Z_{p},\dots,Z_{{p+m}}))E(g(Z_{p},\dots,Z_{{p+l}})).
\Box

8.4. Martyngały i przyrosty martyngałowe

Definicja 8.10

K-wymiarowy proces stochastyczny Z=(Z_{t})_{{t=0}}^{\infty} nazywamy martyngałem gdy

\displaystyle 1. \displaystyle Z_{t}\in L^{1}\;\;\;\mbox{ dla }\;\;\; t=0,1,\dots,
\displaystyle 2. \displaystyle E(Z_{t}|Z_{{t-1}},\dots,Z_{0})=Z_{{t-1}}\;\;\;\mbox{ dla }\;\;\; t=1,2,\dots.
Definicja 8.11

K-wymiarowy proces stochastyczny g=(g_{t})_{{t=0}}^{\infty} nazywamy ciągiem przyrostów martyngałowych gdy

\displaystyle 1. \displaystyle E(g_{t})=0,\;\;\;\mbox{ dla }\;\;\; t=0,1,\dots,
\displaystyle 2. \displaystyle E(g_{t}|g_{{t-1}},\dots,g_{0})=0\;\;\;\mbox{ dla }\;\;\; t=1,2,\dots.
Uwaga 8.8

Jeśli proces Z=(Z_{t})_{{t=0}}^{\infty} jest martyngałem, to proces g=(g_{t})_{{t=0}}^{\infty}, gdzie

g_{0}=Z_{0}-E(Z_{0}),\;\;\; g_{t}=Z_{t}-Z_{{t-1}},\;\;\; t>0,

jest ciągiem przyrostów martyngałowych.

Uwaga 8.9

Jeśli proces g=(g_{t})_{{t=0}}^{\infty} jest ciągiem przyrostów martyngałowych a \mu dowolną stałą, to proces Z=(Z_{t})_{{t=0}}^{\infty}, gdzie

Z_{0}=\mu+g_{0},\;\;\; Z_{t}=Z_{{t-1}}+g_{t},\;\;\; t>0,

jest martyngałem.

Lemat 8.3

Jeśli proces g=(g_{t})_{{t=0}}^{\infty} jest ciągiem przyrostów martyngałowych i g_{t} należą do L^{2} to są one nieskorelowane

Cov(g_{t},g_{s})=0,\;\;\;\mbox{ dla }\;\;\; t\neq s.

Dowód.
Zapiszemy wektory g_{t} i g_{{t+j}}, j>0, jako wektory kolumnowe. E(g_{t})=E(g_{{t+j}})=0 zatem

Cov(g_{t},g_{{t+j}})=E(g_{t}g_{{t+j}}^{T})=E(E(g_{t}g_{{t+j}}^{T}|g_{{t+j-1}},\dots,g_{0}))=
=E(g_{t}E(g_{{t+j}}^{T}|g_{{t+j-1}},\dots,g_{0}))=E(g_{t}\cdot 0)=0.
\Box

Przykład
Biały szum \varepsilon=(\varepsilon _{t}) jest ciągiem przyrostów martyngałowych, a błądzenie przypadkowe czyli proces X=(X_{t})_{{t=0}}^{{\infty}}

X_{0}=\mu+\varepsilon _{0},\;\;\; X_{t}=X_{{t-1}}+\varepsilon _{{t}},\;\;\; t>0,

jest martyngałem.

Twierdzenie 8.6

Centralne Twierdzenie Graniczne ([2] Twierdzenie 23.1).
Jeśli stacjonarny i ergodyczny proces g=(g_{t})_{{t=0}}^{\infty} jest ciągiem przyrostów martyngałowych i g_{t} należą do L^{2}, to

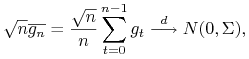\sqrt{n}\overline{g_{n}}=\frac{\sqrt{n}}{n}\sum _{{t=0}}^{{n-1}}g_{t}\stackrel{d}{\longrightarrow}N(0,\Sigma),

gdzie \Sigma=E(g_{0}g_{0}^{T}).

Uwaga 8.10

Powyższe twierdzenie jest uogólnieniem CTG Linderberga-Levy'ego, w którym pominięta została niezależnośc składników.

« 7. Modele nieliniowe  Spis treści  9. Teoria dużej próbki »  

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

strona główna | webmaster | o portalu | pomoc

© Wydział Matematyki, Informatyki i Mechaniki UW, 2009-2010. Niniejsze materiały są udostępnione bezpłatnie na licencji Creative Commons Uznanie autorstwa-Użycie niekomercyjne-Bez utworów zależnych 3.0 Polska.

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego.

Projekt współfinansowany przez Ministerstwo Nauki i Szkolnictwa Wyższego i przez Uniwersytet Warszawski.