Najprostszy model oświetlenia opiera się na założeniu, że przestrzeń, w której znajdują się rysowane obiekty, jest wypełniona światłem, które dochodzi ze wszystkich kierunków z taką samą intensywnością. Założenie to jest nieodległe od prawdy, jeśli scena jest umieszczona w pomieszczeniu o jasnych (np. białych) matowych ścianach i obiekty te są oświetlone przede wszystkim światłem odbitym od ścian. Wzór, który służy do obliczenia intensywności światła odbitego w stronę obserwatora (czyli do obliczenia koloru pikseli) ma postać

Czynnik opisuje intensywność światła rozproszonego w otoczeniu i jest funkcją długości fali świetlnej. Czynnik to albedo powierzchni przedmiotu, które zależy również od długości fali, a także od punktu powierzchni, która nie musi być jednobarwna. Często funkcje długości fali, takie jak , i , są reprezentowane za pomocą trzech wartości odpowiedających barwie czerwonej, zielonej i niebieskiej. W niektórych zastosowaniach to nie wystarczy i trzeba użyć większej liczby próbek, tj. wartości funkcji opisującej oświetlenie dla więcej niż trzech długości fali świetlnej (nawet jeśli potem na monitorze obraz jest wyświetlany za pomocą luminoforów o trzech barwach).

Obrazy wykonane z użyciem tego modelu oświetlenia są całkowicie pozbawione plastyki; jeśli obiekty są jednobarwne (bez tekstury) to wyglądają jak plamy o stałym kolorze.

Wzór

opisuje tzw. lambertowski model odbicia światła, nazwany tak od J.H. Lamberta, który zajmował się nim w 1760r. Oprócz światła rozproszonego w otoczeniu, o intensywności , mamy tu pewną liczbę punktowych źródeł światła. Intensywność oświetlenia powierzchni przez -te źródło jest opisana przez funkcję , zależną od długości fali świetlnej, a także od odległości źródła światła od oświetlanego punktu, jeśli ta odległość jest skończona. Czynnik jest równy lub , co zależy od tego, czy między rozpatrywanym punktem powierzchni i źródłem światła jest jakiś obiekt rzucający cień, czy nie.

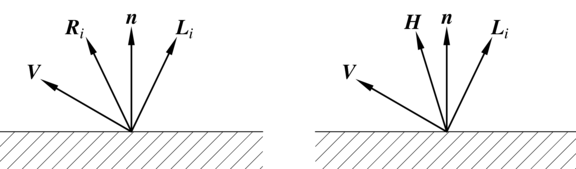
Wektor jest wektorem normalnym powierzchni, a wektor określa kierunek do źródła światła. Kosinus kąta między tymi wektorami jest obliczany przez obliczenie iloczynu skalarnego.

Lambertowski model oświetlenia opiera się na założeniu, że obiekty są idealnie matowe, a zatem światło odbite od powierzchni rozchodzi się we wszystkich kierunkach nad powierzchnią z taką samą intensywnością. Nie ma w tym modelu możliwości otrzymania na obrazie odblasków, które można zaobserwować na powierzchniach błyszczących.

Odblaski są możliwe do uzyskania w modelu opracowanym w 1975r. przez Phong Buoi-Tuonga. Wzór używany do obliczenia intensywności światła odbitego od powierzchni w kierunku obserwatora w tym modelu ma postać

Od wzoru opisującego model lambertowski wzór ten różni się obecnością składnika opisującego odblaski. Funkcja uwzględnia zależność intensywności odblasku od kąta padania światła na powierzchnię i często przyjmowana jest tu funkcja stała. Intensywność światła w odblasku zależy od kąta między wektorem opisującym kierunek do obserwatora i wektorem , którego kierunek odpowiada odbiciu światła padającego z kierunku wektora w idealnym lustrze. Wektor można obliczyć na podstawie wzoru

do którego należy podstawić wektor jednostkowy . Kosinus kąta między wektorami i jest podnoszony do potęgi . Liczba  zależy od ,,stopnia wypolerowania” powierzchni i jest tym większa im bardziej błyszcząca ma być ta powierzchnia. Przyjmowane w praktyce wartości parametru  są w granicach od kilku do kilkuset. Na ogół  jest liczbą całkowitą, ponieważ wtedy -tą potęgę można obliczyć kosztem mnożeń.

Warto zwrócić uwagę na to, że albedo powierzchni (opisane przez funkcję ) nie wpływa na barwę światła w odblaskach. Rzeczywiście, jeśli przyjrzymy się odblaskom na powierzchni fizycznie istniejących przedmiotów, to najczęściej mają one barwę światła padającego na powierzchnię.

Zamiast obliczać wektor , a następnie , możemy wykonać rachunek przybliżony. Mamy , gdzie

(wektory oraz mają długość ). Równość zachodzi w przypadku, gdy wektory , i leżą w jednej płaszczyźnie. Następnie mamy przybliżoną równość

W implementacjach często stosuje się stablicowane z dostatecznie małym krokiem wartości funkcji , co znacznie przyspiesza obliczenia (kosztem pamięci).

Należy podkreślić, że model Phonga jest czysto empiryczny, tj. nie ma on podstaw fizycznych, ale dobierając odpowiednio jego parametry, można osiągnąć dosyć dobre przybliżenie wyglądu różnych materiałów na obrazie. Najczęściej obiekty narysowane za pomocą tego modelu mają wygląd nieco ,,plastikowy”. Jest to spowodowane przez dość dobre przybliżenie skutków odbicia światła od przedmiotów wykonanych z plastiku.

Najprostsza metoda cieniowania polega na obliczeniu barwy jednego piksela i nadaniu tej samej wartości wszystkim pikselom, które należą do obrazu np. danego wielokąta. Metoda ta jest najprostsza i najszybsza, ale daje obrazy z wyraźnie widocznymi wspólnymi krawędziami ścian, co w sytuacji gdy te ściany stanowią przybliżenie gładkiej powierzchni zakrzywionej jest niepożądane (to jest tzw. efekt Macha).

Metoda cieniowania Gourauda jest stosowana najczęściej do trójkątów — inne wielokąty są w celu cieniowania triangulowane. Metoda ta polega na obliczeniu (przy użyciu dowolnego modelu oświetlenia) barw wierzchołków trójkąta, a następnie barwa każdego piksela jest obliczana w drodze interpolacji liniowej barw wierzchołków (wygodnie jest to opisać przy użyciu współrzędnych barycentrycznych na płaszczyźnie).

Zastosowanie cieniowania metodą Gourauda powoduje usunięcie lub znaczne osłabienie efektu Macha — barwa pikseli w pobliżu wspólnej krawędzi trójkątów zmienia się w sposób ciągły — ale zawodzi w przypadku, gdy zastosowany model oświetlenia uwzględnia odbicie zwierciadlane (tak jak model Phonga). Można bowiem zgubić odblaski, które leżą wewnątrz obrazu trójkąta, a także otrzymać kanciaste odblaski na powierzchni, która ma wyglądać jak gładka.

W metodzie cieniowania opracowanej przez Phong Buoi-Tuonga określamy we wszystkich wierzchołkach trójkątnych ścian wektor normalny powierzchni, którą chcemy przybliżać za pomocą tych ścian. Następnie, dla każdego piksela, obliczamy ,,wektor normalny” powierzchni w drodze interpolacji wektorów normalnych w narożnikach i po unormowaniu podstawiamy go do wzoru odpowiadającego wybranemu modelowi oświetlenia. Metoda ta jest bardzo skuteczna, ale wymaga znacznie więcej obliczeń niż cieniowanie Gourauda.

,,Wektor normalny” powierzchni w wierzchołkach trójkąta może być przyjmowany na różne sposoby. Jeśli trójkąty przybliżają powierzchnię znaną (np. płat Béziera), to można obliczyć wektor normalny tej powierzchni w punkcie, który odpowiada wierzchołkowi. Jeśli trójkąty przybliżają powierzchnię daną w postaci niejawnej, tj. równaniem , to najlepiej jest (jeśli to możliwe) obliczyć gradient funkcji . Jeśli dysponujemy tylko trójkątami, to można przyjąć wektor, który jest średnią arytmetyczną wektorów normalnych wszystkich trójkątów, do których należy ten wierzchołek. Zwróćmy uwagę, że wyświetlając wielokąt w OpenGL-u, możemy dla każdego wierzchołka podać inny ,,wektor normalny” (o dowolnym kierunku).

Cieniowanie jest najczęściej realizowane za pomocą sprzętu, np. podsystemu graficznego stacji roboczej, albo akceleratora w pececie. Metoda cieniowania jest wtedy ukryta przed programem i różna (Gouraud albo Phong) w różnych urządzeniach realizujących ten sam interfejs programisty (np. OpenGL). W tanim sprzęcie do użytku domowego cieniowanie Phonga to jeszcze rzadkość, choć sytuacja zmienia się. Nowe akceleratory graficzne mogą wykonywać programy wprowadzone przez aplikację. W zamierzeniu umożliwia to stosowanie różnych sposobów przetwarzania tekstury nakładanej na wyświetlane powierzchnie. W szczególności można używać własnych procedur cieniowania, a także nakładać opisane dalej tekstury odkształceń.

W każdym modelu oświetlenia uwzględniającym kierunek padania światła na powierzchnię zasadniczą rolę odgrywa wektor normalny, i jak wynika z rozważań nad cieniowaniem Phonga, kolorując obraz powierzchni można trochę oszukiwać zmysł wzroku, wybierając wektor niezupełnie normalny. Stąd już tylko krok do określania wektora normalnego za pomocą arbitralnej funkcji, dzięki czemu daje się symulować niewielkie odkształcenia i chropowatość powierzchni.