Zagadnienia
11. Śledzenie promieni
Śledzenie promieni (ang. ray tracing) jest pierwszą metodą wizualizacji obiektów trójwymiarowych, od której ludzie zaczęli mówić o ,,fotorealistycznych” obrazach utworzonych przez komputer. Można ją scharakteryzować za pomocą następujących uwag:
-
Metoda ta jest algorytmem widoczności (przestrzeni obrazu), co prawda niezbyt sprawnym i dlatego często bywa on wspomagany innymi algorytmami widoczności.
-
Jest to również algorytm wyznaczania cieni.
-
Najbardziej charakterystyczna jest możliwość symulowania wielokrotnych odbić zwierciadlanych i załamań światła. Bardziej ograniczone są możliwości otrzymywania półcieni.
-
Istnieje możliwość stosunkowo łatwego połączenia metody śledzenia promieni z konstrukcyjną geometrią brył i z wizualizacją objętościową (można więc tworzyć obrazy dymu, mgły itd.). Klasa dopuszczalnych obiektów, które można wizualizować tą metodą jest bardzo obszerna.
-
Łatwo można przeciwdziałać zjawisku aliasu, możliwe są też efekty specjalne, takie jak symulowanie głębi ostrości obiektywu i inne.
Ceną za to wszystko jest duża ilość obliczeń wykonywanych w tym algorytmie, czyli długi (rzędu kilku sekund do nawet godzin) czas tworzenia obrazu. Nie jest to więc algorytm nadający się do wykorzystania w programach interakcyjnych jako główna metoda wizualizacji trójwymiarowych scen.
11.1. Zasada działania algorytmu
W metodzie śledzenia promieni kolejno dla każdego piksela należy
obliczyć jego barwę, tj. intensywność światła, która dochodzi
do obserwatora ,,przez ten piksel”. W tym celu należy przeszukać
tzw. drzewo promieni.
Korzeniem tego drzewa jest tzw. promień pierwotny, czyli
półprosta o początku w położeniu obserwatora, ,,przechodząca przez
piksel”. Dla danego promienia należy wyznaczyć punkt przecięcia z
powierzchnią obiektu, najbliższy obserwatora. Punkt ten jest początkiem
tzw. promieni wtórnych, których może być kilka (zwykle co
najmniej ![]() , ale bywa też kilkanaście lub nawet kilkadziesiąt).
, ale bywa też kilkanaście lub nawet kilkadziesiąt).
Dla każdego z promieni wtórnych wykonuje się podobne obliczenie jak dla promieni pierwotnych. Oczywiście, istnieją ograniczenia w generowaniu promieni wtórnych, które mają na celu zapewnienie własności stopu algorytmu. Dla każdego promienia oblicza się intensywność światła niesionego przez ten promień do jego punktu początkowego. Następnie w punkcie początkowym promieni wtórnych stosuje się odpowiedni model oświetlenia w celu obliczenia intensywności światła niesionego w kierunku początku promienia, który określił ten punkt początkowy promieni wtórnych. Intensywność światła niesionego przez promień pierwotny jest używana do obliczenia barwy piksela.
Dróg, po których porusza się światło jest niewyobrażalnie dużo i dlatego należy wybrać możliwie niewielki zbiór promieni wtórnych, które będą wystarczające do obliczenia intensywności światła z dostateczną dokładnością. Wśród promieni wtórnych wyróżniamy:
-
promienie odbite, których kierunek wynika z odbicia promienia pierwotnego lub wtórnego niższego rzędu w sposób zwierciadlany:
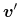
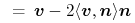
jeśli 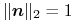 ,
,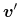
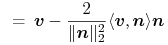
jeśli 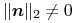 .
.Uwaga 1: Można zaburzać wektor
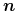 , nakładając na
powierzchnię teksturę odkształceń.
, nakładając na
powierzchnię teksturę odkształceń.
Uwaga 2: Czasem wykonuje się też śledzenie promieni odbitych w inny sposób. -
promienie załamane — dla obiektów przezroczystych. Prawo załamania światła jest opisane wzorem
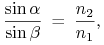
w którym
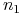 i
i 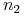 są współczynnikami załamania światła
w poszczególnych ośrodkach. Nawiasem mówiąc, istnieją ośrodki,
których współczynnik załamania światła zmienia się w sposób
ciągły, np. powietrze o różnej temperaturze w różnych miejscach,
lub roztwór soli o niejednolitym stężeniu. Światło w takich ośrodkach
porusza się po krzywych, wskutek czego powstają zjawiska takie jak
fatamorgana.
są współczynnikami załamania światła
w poszczególnych ośrodkach. Nawiasem mówiąc, istnieją ośrodki,
których współczynnik załamania światła zmienia się w sposób
ciągły, np. powietrze o różnej temperaturze w różnych miejscach,
lub roztwór soli o niejednolitym stężeniu. Światło w takich ośrodkach
porusza się po krzywych, wskutek czego powstają zjawiska takie jak
fatamorgana. -
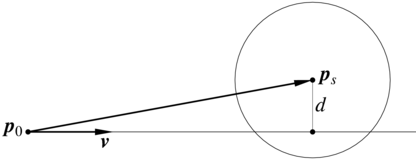
promienie bezpośredniego oświetlenia — ich kierunki są określone przez położenia źródeł światła. Promienie te służą do uwzględnienia w modelu oświetlenia punktu, który jest ich początkiem, światła dochodzącego bezpośrednio od źródeł. Śledzenie tych promieni ma na celu wyznaczenie odległości od źródeł światła oraz wykrycie ewentualnych obiektów rzucających cień.
Program przeszukuje drzewo promieni metodą DFS. Promienie wtórne są generowane wtedy, gdy są spełnione następujące warunki:
-
Przypuśćmy, że w obliczeniach intensywności światła niesionego przez promień jest obliczana zgodnie z modelem oświetlenia Phonga. Dla każdego promienia obliczamy jego wagę, czyli współczynnik, który określa wpływ intensywności światła niesionego przez ten promień na ostateczną barwę piksela. Dla promieni pierwotnych współczynnik ten jest równy
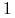 . Jeśli na przykład
stosujemy model oświetlenia Phonga, to generując promień wtórny,
którego kierunek jest określony przez wektor
. Jeśli na przykład
stosujemy model oświetlenia Phonga, to generując promień wtórny,
którego kierunek jest określony przez wektor 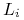 , obliczamy jego wagę
mnożąc wagę promienia niższego rzędu przez czynnik
, obliczamy jego wagę
mnożąc wagę promienia niższego rzędu przez czynnik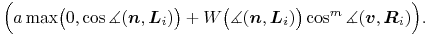
Jeśli otrzymana waga promienia jest mniejsza niż ustalona wartość progowa, to nie tracimy czasu na śledzenie tego promienia. Dla przykładu, w programie RayShade domyślna wartość progowa (odpowiedni parametr nazywa się cutoff) jest równa
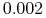 .
. -
Program śledzenia promieni może też ustalić arbitralne ograniczenie wysokości drzewa promieni (np. w RayShade mamy parametr maxdepth o domyślnej wartości
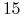 ). Ten drugi sposób
gwarantuje własność stopu algorytmu,
natomiast pierwszy ma większe znaczenie dla szybkości obliczeń.
). Ten drugi sposób
gwarantuje własność stopu algorytmu,
natomiast pierwszy ma większe znaczenie dla szybkości obliczeń.
11.2. Wyznaczanie przecięć promieni z obiektami
Najwięcej czasu w śledzeniu promieni, do ![]() %, zajmuje obliczanie
punktów przecięcia promieni z powierzchniami obiektów. Wyznaczanie
przecięć jest rozwiązywaniem równań (na ogół nieliniowych) i składa
się z dwóch zasadniczych etapów: lokalizacji rozwiązań i obliczania ich
z dużą dokładnością. Równania te mają postać zależną od
reprezentacji obiektu. Zakładamy, że promień jest reprezentowany
w postaci parametrycznej:
%, zajmuje obliczanie
punktów przecięcia promieni z powierzchniami obiektów. Wyznaczanie
przecięć jest rozwiązywaniem równań (na ogół nieliniowych) i składa
się z dwóch zasadniczych etapów: lokalizacji rozwiązań i obliczania ich
z dużą dokładnością. Równania te mają postać zależną od
reprezentacji obiektu. Zakładamy, że promień jest reprezentowany
w postaci parametrycznej:
-
Jeśli obiekt jest powierzchnią parametryczną,

(litera
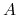 oznacza dziedzinę powierzchni
oznacza dziedzinę powierzchni 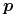 ), to punkt
), to punkt 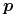 ,
wspólny dla promienia i płata, spełnia równanie
,
wspólny dla promienia i płata, spełnia równanie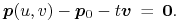
Powyższe równanie jest układen trzech równań z trzema niewiadomymi,
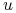 ,
, 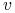 oraz
oraz 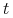 . Warto zauważyć, że ze względu na niewiadomą
. Warto zauważyć, że ze względu na niewiadomą 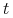 wszystkie te równania są liniowe, co umożliwia wyeliminowanie tej
niewiadomej, tj. otrzymanie dwóch równań, w których niewiadoma ta
nie występuje. Daje to możliwość opracowania szybszego i
pewniejszego algorytmu numerycznego rozwiązania tego układu
(pamiętajmy, że mamy do czynienia z układami równań nieliniowych, dla
rozwiązania których sprawą zasadniczą jest znalezienie przybliżeń
początkowych rozwiązań, oraz rozstrzygnięcie, czy wszystkie
rozwiązania zostały znalezione).
wszystkie te równania są liniowe, co umożliwia wyeliminowanie tej
niewiadomej, tj. otrzymanie dwóch równań, w których niewiadoma ta
nie występuje. Daje to możliwość opracowania szybszego i
pewniejszego algorytmu numerycznego rozwiązania tego układu
(pamiętajmy, że mamy do czynienia z układami równań nieliniowych, dla
rozwiązania których sprawą zasadniczą jest znalezienie przybliżeń
początkowych rozwiązań, oraz rozstrzygnięcie, czy wszystkie
rozwiązania zostały znalezione). -
Jeśli powierzchnię reprezentujemy w postaci niejawnej:
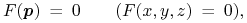
to po wstawieniu parametrycznej reprezentacji promienia dostajemy równanie skalarne z jedną niewiadomą
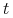 :
: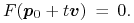
Zauważmy, że równania liniowe otrzymamy wtedy, gdy rozpatrywana powierzchnia jest płaszczyzną, daną w postaci
Wysiłek mający na celu przyspieszenie działania programu do śledzenia promieni może mieć na celu
-
zmniejszenie kosztu wyznaczania punktu przecięcia promienia z obiektem, albo
-
zmniejszenie liczby par promień/obiekt, dla których poszukuje się przecięć (zwróćmy uwagę, że jeśli scena składa się z wielu obiektów, to każdy promień przecina tylko nieliczne z nich).
Ilość obliczeń w śledzeniu promieni jest taka, że niezależnie od mocy obliczeniowej komputera (która rośnie w zdumiewającym, ale i tak zbyt wolnym tempie1097th rule of acquisition: “Enough… is never enough.”), do realizacji pierwszego z powyższych celów wciąż jeszcze ludzie sięgają po asembler i optymalizują na tym poziomie procedury jak mało które. Przedtem lepiej jest jednak wybrać algorytm, który wykonuje jak najmniej działań, bo asembler to ostateczność.
Przykład 1
Porównamy dwie metody obliczania punktu przecięcia promienia ze sferą.
Zakładamy, że ![]() , a ponadto reprezentacja sfery zawiera
obliczony kwadrat promienia
, a ponadto reprezentacja sfery zawiera
obliczony kwadrat promienia ![]() (aby nie liczyć go ponownie dla każdego
promienia).
(aby nie liczyć go ponownie dla każdego
promienia).
Metoda 1: Równania promienia i sfery mają postać
![\displaystyle\left[\begin{array}[]{c}x\\
y\\
z\end{array}\right]\:=\:\left[\begin{array}[]{c}x_{0}\\
y_{0}\\
z_{0}\end{array}\right]+t\left[\begin{array}[]{c}x_{v}\\
y_{v}\\
z_{v}\end{array}\right],](wyklady/gk1/mi/mi977.png) |
|||
Po podstawieniu otrzymujemy równanie ![]() ,
w którym
,
w którym
dalej możemy obliczyć ![]() i jeśli
i jeśli ![]() to
to
![]() . Przed sprawdzeniem, czy istnieją
rozwiązania, trzeba wykonać
. Przed sprawdzeniem, czy istnieją
rozwiązania, trzeba wykonać ![]() mnożeń i
mnożeń i ![]() dodawań, a potem obliczyć
dodawań, a potem obliczyć
![]() pierwiastek i wykonać
pierwiastek i wykonać ![]() dodawania.
dodawania.
Metoda 2: Jeśli ![]() , to możemy obliczyć
, to możemy obliczyć
(liczymy ![]() , a następnie
, a następnie
![]() i nie wyciągamy pierwiastka). Przed
sprawdzeniem, czy istnieją rozwiązania (czyli porównaniem
i nie wyciągamy pierwiastka). Przed
sprawdzeniem, czy istnieją rozwiązania (czyli porównaniem ![]() i
i ![]() ) wystarczy wykonać
) wystarczy wykonać ![]() mnożeń i
mnożeń i ![]() dodawań, dalej liczymy
dodawań, dalej liczymy
Jeśli rozwiązania istnieją, to dokończenie ich obliczania wymaga jeszcze
![]() mnożeń i
mnożeń i ![]() dodawań i jednego pierwiastkowania. Często jednak interesuje
nas tylko szybkie zbadanie, czy promień przecina się ze sferą, jeśli
wykorzystujemy sfery jako bryły otaczające bardziej skomplikowane obiekty.
dodawań i jednego pierwiastkowania. Często jednak interesuje
nas tylko szybkie zbadanie, czy promień przecina się ze sferą, jeśli
wykorzystujemy sfery jako bryły otaczające bardziej skomplikowane obiekty.
Przykład 2
Należy znaleźć przecięcie promienia z trójkątem (lub ogólniej, z płaskim wielokątem). Aby znaleźć punkt wspólny promienia z płaszczyzną trójkąta, wystarczy rozwiązać układ równań liniowych, ale znacznie trudniejszym problemem jest rozstrzygnięcie, czy punkt wspólny promienia i płaszczyzny należy do trójkąta.
Dla trójkąta można użyć następującego algorytmu. W pierwszym kroku
dokonujemy takiej zmiany układu współrzędnych, aby promień pokrywał się
z dodatnią lub ujemną półosią ![]() . W tym celu do wierzchołków
trójkąta dodajemy odpowiednie przesunięcie, a następnie konstruujemy
odbicie Householdera, które przekształci wektor kierunkowy promienia na
wersor osi
. W tym celu do wierzchołków
trójkąta dodajemy odpowiednie przesunięcie, a następnie konstruujemy
odbicie Householdera, które przekształci wektor kierunkowy promienia na
wersor osi ![]() lub wektor do niego przeciwny (zakładamy, że wektor
kierunkowy promienia zawsze jest jednostkowy).
lub wektor do niego przeciwny (zakładamy, że wektor
kierunkowy promienia zawsze jest jednostkowy).
W drugim kroku rozwiązujemy układ równań z macierzą utworzoną ze współrzędnych w nowym układzie wierzchołków trójkąta:
![\displaystyle\left[\begin{array}[]{ccc}x_{0}&x_{1}&x_{2}\\
y_{0}&y_{1}&y_{2}\\
1&1&1\end{array}\right]\left[\begin{array}[]{c}a_{0}\\
a_{1}\\
a_{2}\end{array}\right]=\left[\begin{array}[]{c}0\\
0\\
1\end{array}\right].](wyklady/gk1/mi/mi968.png) |
W wyniku otrzymujemy współrzędne barycentryczne ![]() punktu
przecięcia prostej, na której leży promień z płaszczyzną trójkąta.
Punkt przecięcia należy do trójkąta, jeśli wszystkie te współrzędne
są nieujemne.
punktu
przecięcia prostej, na której leży promień z płaszczyzną trójkąta.
Punkt przecięcia należy do trójkąta, jeśli wszystkie te współrzędne
są nieujemne.
Punkt przecięcia w przestrzeni możemy obliczyć ze wzoru
![]() . Następnie obliczamy
parametr promienia
. Następnie obliczamy
parametr promienia ![]() i badamy, czy
i badamy, czy ![]() .
.
Współrzędne barycentryczne możemy wykorzystać do cieniowania (np. metodą Phonga) lub do obliczenia współrzędnych tekstury nakładanej na trójkąt.
Aby obliczyć przecięcie promienia z dowolnym wielokątem płaskim, możemy w podobny sposób sprowadzić zadanie do problemu dwuwymiarowego. Ze względów praktycznych (m.in. dla wygody cieniowania) wielokąty dowolne warto zastąpić odpowiednimi trójkątami przed przystąpieniem do śledzenia promieni i skorzystać z procedury dla trójkątów.
Przykład 3
Jedną z największych zalet śledzenia promieni jest możliwość
,,dorabiania” obsługi nietypowych obiektów.
Możemy określić ,,rurkę Béziera”; jest to powierzchnia składająca
się z punktów położonych w danej odległości ![]() od ustalonej krzywej
Béziera
od ustalonej krzywej
Béziera ![]() .
Nie znam ,,gotowego” programu, który dopuszcza takie obiekty,
a potrzebowałem przedstawić je na obrazkach. Obrazy takich powierzchni
są na rysunku 1.6. Do ich utworzenia posłużyła mi
procedura, którą tu opiszę.
.
Nie znam ,,gotowego” programu, który dopuszcza takie obiekty,
a potrzebowałem przedstawić je na obrazkach. Obrazy takich powierzchni
są na rysunku 1.6. Do ich utworzenia posłużyła mi
procedura, którą tu opiszę.
Krzywa stanowiąca ,,oś” rurki jest stopnia ![]() i jej reprezentacją jest
ciąg punktów kontrolnych
i jej reprezentacją jest
ciąg punktów kontrolnych ![]() . Promień jest dany za
pomocą początku
. Promień jest dany za
pomocą początku ![]() i jednostkowego wektora
i jednostkowego wektora ![]() . Przypuśćmy,
że punkt
. Przypuśćmy,
że punkt ![]() jest początkiem układu współrzędnych, zaś wektor
jest początkiem układu współrzędnych, zaś wektor
![]() jest wersorem osi
jest wersorem osi ![]() . Wtedy mamy wyznaczyć zbiór liczb
. Wtedy mamy wyznaczyć zbiór liczb ![]() leżących w przedziale
leżących w przedziale ![]() , takich że punkt
, takich że punkt ![]() leży
w odległości
leży
w odległości ![]() od osi
od osi ![]() . Jeśli funkcje
. Jeśli funkcje ![]() ,
, ![]() i
i ![]() są
wielomianami opisującymi współrzędne krzywej
są
wielomianami opisującymi współrzędne krzywej ![]() , to mamy do
wyznaczenia zbiór rozwiązań równania
, to mamy do
wyznaczenia zbiór rozwiązań równania
Jest to równanie algebraiczne stopnia ![]() ; współczynniki wielomianu
po lewej stronie w bazie Bernsteina są dosyć łatwe do obliczenia
(procedura mnożenia wielomianów danych w tej bazie jest opisana
w książce Podstawy modelowania krzywych i powierzchni). Po
znalezieniu tych współczynników można zastosować procedurę numeryczną
opartą na rekurencyjnym połowieniu dziedziny krzywej oraz na metodzie
Newtona. Pozostają dwa dodatkowe problemy: na ogół promień nie spełnia
przyjętych założeń. Ponadto należy wyznaczyć punkt przecięcia
i wektor normalny (na podstawie którego będą wyznaczane promienie odbite
i oświetlenie).
; współczynniki wielomianu
po lewej stronie w bazie Bernsteina są dosyć łatwe do obliczenia
(procedura mnożenia wielomianów danych w tej bazie jest opisana
w książce Podstawy modelowania krzywych i powierzchni). Po
znalezieniu tych współczynników można zastosować procedurę numeryczną
opartą na rekurencyjnym połowieniu dziedziny krzywej oraz na metodzie
Newtona. Pozostają dwa dodatkowe problemy: na ogół promień nie spełnia
przyjętych założeń. Ponadto należy wyznaczyć punkt przecięcia
i wektor normalny (na podstawie którego będą wyznaczane promienie odbite
i oświetlenie).
Aby rozwiązać pierwszy problem wystarczy przedstawić krzywą ![]() w takim układzie współrzędnych, w którym promień pokrywa się
z dodatnią lub ujemną półosią
w takim układzie współrzędnych, w którym promień pokrywa się
z dodatnią lub ujemną półosią ![]() . Wystarczy dokonać przesunięcia,
które przekształci punkt
. Wystarczy dokonać przesunięcia,
które przekształci punkt ![]() na początek układu, a następnie
odbicia Householdera, które przekształci wektor
na początek układu, a następnie
odbicia Householdera, które przekształci wektor ![]() na wektor
na wektor
![]() . Przekształceniom tym poddajemy punkty kontrolne
. Przekształceniom tym poddajemy punkty kontrolne
![]() .
.
Obliczenie punktu przecięcia i wektora normalnego polega na drobnym
oszustwie. Mając rozwiązanie ![]() równania możemy obliczyć punkt
równania możemy obliczyć punkt
![]() i wektor
i wektor ![]() . Użyjemy ich do określenia walca
o promieniu
. Użyjemy ich do określenia walca
o promieniu ![]() , którego oś jest określona przez ten punkt i wektor.
Przyjmiemy, że punkt przecięcia promienia z rurką Béziera i wektor
normalny są tożsame z punktem przecięcia i wektorem normalnym przecięcia
promienia z tym walcem. Dla potrzeb wykonania obrazu takie przybliżenie
jest wystarczające. Oczywiście, sprawdzamy przy tym, czy parametr
promienia jest dodatni (bo promień jest półprostą) i jeśli mamy dwa
punkty wspólne promienia i walca, to wybieramy punkt położony
w odległości
, którego oś jest określona przez ten punkt i wektor.
Przyjmiemy, że punkt przecięcia promienia z rurką Béziera i wektor
normalny są tożsame z punktem przecięcia i wektorem normalnym przecięcia
promienia z tym walcem. Dla potrzeb wykonania obrazu takie przybliżenie
jest wystarczające. Oczywiście, sprawdzamy przy tym, czy parametr
promienia jest dodatni (bo promień jest półprostą) i jeśli mamy dwa
punkty wspólne promienia i walca, to wybieramy punkt położony
w odległości ![]() od punktu
od punktu ![]() .
.
11.3. Techniki przyspieszające
11.3.1. Bryły otaczające i hierarchia sceny
Obliczanie przecięć ma na celu znalezienie punktów przecięcia promienia z obiektem, albo stwierdzenie, że ich nie ma. O ile to pierwsze może wymagać dość kosztownych obliczeń, których nie da się uprościć, istnieje szybki test, który pozwala wykryć większość par promień/obiekt, które nie mają punktów wspólnych. Polega on na wprowadzeniu brył otaczających każdy obiekt w scenie. Jeśli obiekt jest powierzchnią algebraiczną lub bryłą wielościenną, rozwiązywanie równań, prowadzące do stwierdzenia, że rozwiązań nie ma, zajmuje zwykle dość sporo czasu (zależnie od stopnia powierzchni lub liczby ścian). Jeśli dla takiego obiektu wskażemy kulę, wewnątrz której ten obiekt jest zawarty, to możemy najpierw sprawdzić, czy promień przecina się ze sferą — brzegiem kuli i wykonywać dalsze, bardziej kosztowne obliczenia tylko w przypadku uzyskania odpowiedzi twierdzącej.
Można wprowadzać inne bryły otaczające, np. kostki (tj. prostopadłościany o ścianach równoległych do płaszczyzn układu), albo
elipsoidy (przydatne wtedy, gdy obiekt ma wydłużony kształt). Aby
dowiedzieć się, czy promień przecina prostopadłościan, możemy
zastosować algorytm Lianga-Barsky'ego (opisany
w p. 3.1.3). Poniżej jest przykład realizacji tego
algorytmu w zastosowaniu do tego testu. Promień jest reprezentowany przez
punkt początkowy ![]() i wektor
i wektor ![]() , a parametr
, a parametr ![]() reprezentuje
prostopadłościan.
reprezentuje
prostopadłościan.
| function TestBoxRay ( |
| var |
| function Test ( |
| … Ta funkcja jest identyczna jak na str. 3.1.3 |
| end {Test}; |
| begin {TestBoxRay} |
| |
| if Test ( |
| if Test ( |
| if Test ( |
| if Test ( |
| if Test ( |
| if Test ( |
| return true; |
| return false |
| end {TestBoxRay}; |
Wprowadzenie bryły otaczającej dla każdego obiektu zmniejsza średni koszt wyznaczania przecięć (jeśli promienie są rozłączne z większością obiektów), ale nie obniża złożoności obliczeniowej algorytmu, bo nadal trzeba przetworzyć tyle samo par promień/obiekt. Można jednak wprowadzić hierarchię obiektów, której reprezentacja ma postać drzewa; korzeniem drzewa jest cała scena, a poddrzewa opisują zbiory obiektów znajdujących się blisko siebie. W każdym wierzchołku tworzymy reprezentację bryły otaczającej wszystkie obiekty reprezentowane przez ten wierzchołek i jego poddrzewa. Podczas śledzenia promieni przeszukujemy drzewo hierarchii sceny metodą DFS, pomijając każde poddrzewo, z którego bryłą otaczającą promień jest rozłączny.
Przykładowa scena przedstawiona na rysunku 7.5 została
opisana w postaci hierarchicznej — sąsiednie obiekty (kule i walce)
były łączone w pary, pary w czwórki itd., czyli drzewo wprowadzonej
hierarchii było binarne. Dla każdego wierzchołka drzewa (oprócz liści)
została znaleziona kostka otaczająca. Utworzenie obrazu w rozdzielczości
![]() metodą, w której stwierdzenie, że promień nie przecina
się z kostką powodowało pominięcie testów przecinania promienia
z obiektami w odpowiednim poddrzewie, trwało
metodą, w której stwierdzenie, że promień nie przecina
się z kostką powodowało pominięcie testów przecinania promienia
z obiektami w odpowiednim poddrzewie, trwało ![]() s. Pominięcie tych
testów i sprawdzanie dla każdego promienia po kolei istnienia przecięć
z wszystkimi obiektami trwało (nieistotne, na jakim sprzęcie, ważne, że
na tym samym)
s. Pominięcie tych
testów i sprawdzanie dla każdego promienia po kolei istnienia przecięć
z wszystkimi obiektami trwało (nieistotne, na jakim sprzęcie, ważne, że
na tym samym) ![]() s., tj. ok.
s., tj. ok. ![]() razy dłużej.
razy dłużej.
Jeśli nie ma ,,gotowej” hierarchii sceny, jest tylko lista obiektów, z których scena się składa, to można taką hierarchię wprowadzić ,,sztucznie”. Praktyczny sposób polega na znalezieniu bryły otaczającej (np. prostopadłościanu) dla każdego obiektu, a następnie na zbudowaniu drzewa binarnego, metodą łączenia wierzchołków w pary. Obiekty geometryczne, z których składa się scena, zostają liścmi drzewa. Dla każdego (nowego, wewnętrznego) wierzchołka znajdujemy bryłę otaczającą sumę obiektów w poddrzewach. Dwa wierzchołki do połączenia wybieramy tak, aby otrzymać nowy wierzchołek, którego bryła otaczająca jest najmniejsza (np. ma najmniejszą średnicę; to jest algorytm zachłanny, który może nie dać optymalnego drzewa, ale jest stosunkowo prosty i skuteczny). W tym celu można użyć kolejki priorytetowej, np. w postaci kopca. Dla scen złożonych z dużej liczby obiektów takie postępowanie jest dość kosztowne, ale jest ono opłacalne dzięki oszczędności czasu podczas właściwego śledzenia promieni.
11.3.2. Drzewa ósemkowe
Niezależnie od hierarchii sceny, wynikającej ze sposobu jej modelowania, można zmniejszyć złożoność obliczeniową śledzenia promieni za pomocą drzewa ósemkowego, które wprowadza hierarchię wynikającą z rozmieszczenia poszczególnych obiektów w przestrzeni. Drzewo należy utworzyć przed przystąpieniem do śledzenia promieni, dokonując adaptacyjnego rekurencyjnego podziału kostki zawierającej scenę. Adaptacja ta ma na celu skojarzenie z każdym węzłem drzewa możliwie krótkiej listy obiektów, które mają niepuste przecięcie z boksem reprezentowanym przez ten węzeł. Trudność, którą trzeba przy tym pokonać polega na tym, że należy unikać powielania wskaźników do tego samego obiektu w wielu takich listach.
Reguły adaptacyjnego podziału są następujące: kostkę dzielimy na mniejsze, jeśli istnieje obiekt, który
-
jest zawarty w jednej z kostek, które powstałyby z podziału kostki danej, lub
-
ma średnicę istotnie mniejszą (np.
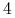 razy) niż średnica
kostki (nawet, jeśli ma on niepuste przecięcia z wszystkimi kostkami
mniejszymi).
razy) niż średnica
kostki (nawet, jeśli ma on niepuste przecięcia z wszystkimi kostkami
mniejszymi).
Można arbitralnie ograniczyć wysokość drzewa (tj. głębokość podziału), a ponadto nie dzielić kostki wtedy, gdy nie spowoduje to otrzymania istotnie krótszych list obiektów.
Mając zbudowane drzewo można przystąpić do śledzenia promieni. Dla
ustalonego promienia wybieramy pewien punkt ![]() (np. początek
promienia). Znając jego współrzędne, możemy (zaczynając od korzenia)
znaleźć wszystkie węzły , które reprezentują kostki zawierające punkt
(np. początek
promienia). Znając jego współrzędne, możemy (zaczynając od korzenia)
znaleźć wszystkie węzły , które reprezentują kostki zawierające punkt
![]() . Wyznaczamy punkty przecięcia promienia z obiektami umieszczonymi
w listach obiektów tych kostek. Następnie wyznaczamy punkt przecięcia
promienia i ściany kostki i znajdujemy kostkę, do której promień ,,
wchodzi” w tym punkcie. Wyznaczamy przecięcia promienia z obiektami
znajdującymi się w kostkach zawierających ten punkt (w drodze od korzenia
do liścia) itd. Procedura kończy działanie po znalezieniu punktu
przecięcia promienia z obiektem — jeśli znajdziemy więcej niż jeden
taki punkt (dla obiektów w liście pewnej kostki), to wybieramy punkt
najbliżej początku promienia. Możemy też zakończyć procedurę w chwili
wyjścia poza całą kostkę (bez znalezienia punktu przecięcia).
. Wyznaczamy punkty przecięcia promienia z obiektami umieszczonymi
w listach obiektów tych kostek. Następnie wyznaczamy punkt przecięcia
promienia i ściany kostki i znajdujemy kostkę, do której promień ,,
wchodzi” w tym punkcie. Wyznaczamy przecięcia promienia z obiektami
znajdującymi się w kostkach zawierających ten punkt (w drodze od korzenia
do liścia) itd. Procedura kończy działanie po znalezieniu punktu
przecięcia promienia z obiektem — jeśli znajdziemy więcej niż jeden
taki punkt (dla obiektów w liście pewnej kostki), to wybieramy punkt
najbliżej początku promienia. Możemy też zakończyć procedurę w chwili
wyjścia poza całą kostkę (bez znalezienia punktu przecięcia).
Ponieważ pewne obiekty mogą być obecne w listach obiektów więcej niż
jednej kostki, więc warto zapobiec wykonywaniu pełnej procedury
wyznaczania przecięć danego promienia z tym samym obiektem, jeśli
występuje on w liście po raz drugi. Skuteczny sposób jest następujący:
opis obiektu występuje ,,w jednym egzemplarzu”, a element listy
w kostce składa się ze wskaźnika do tego opisu i wskaźnika do następnego
elementu. W opisie obiektu występuje pomocniczy atrybut, będący liczbą
całkowitą, o początkowej wartości ![]() . Kolejno przetwarzanym promieniom
nadajemy kolejne numery
. Kolejno przetwarzanym promieniom
nadajemy kolejne numery ![]() . Przed wyznaczaniem przecięcia
promienia z obiektem sprawdzamy, czy numer promienia różni się od atrybutu
w obiekcie. Jeśli tak, to wykonujemy pełną procedurę wyznaczania
przecięcia i przypisujemy atrybutowi obiektu numer bieżącego promienia.
W przeciwnym razie parę tę już sprawdzaliśmy. Zakres liczb całkowitych
. Przed wyznaczaniem przecięcia
promienia z obiektem sprawdzamy, czy numer promienia różni się od atrybutu
w obiekcie. Jeśli tak, to wykonujemy pełną procedurę wyznaczania
przecięcia i przypisujemy atrybutowi obiektu numer bieżącego promienia.
W przeciwnym razie parę tę już sprawdzaliśmy. Zakres liczb całkowitych
![]() -bitowych jest na tyle duży, aby można było prześledzić
dostateczną liczbę promieni nawet dla obrazów o bardzo dobrej jakości.
-bitowych jest na tyle duży, aby można było prześledzić
dostateczną liczbę promieni nawet dla obrazów o bardzo dobrej jakości.
Duże puste obszary są reprezentowane przez stosunkowo duże puste kostki. Stosując drzewa ósemkowe, najwięcej czasu zużywa się na wyznaczanie sąsiada, tj. najmniejszej kostki, której ściana przylega do ściany kostki bieżącej i do której promień ,,wchodzi”. Przeszukiwanie drzewa można zacząć
-
od korzenia — wtedy czas znajdowania sąsiada jest proporcjonalny do poziomu w drzewie poszukiwanej kostki, albo
-
od kostki bieżącej (idziemy w górę, a następnie w dół) — wtedy czas zależy od poziomu ,,najmniejszego wspólnego przodka” kostki bieżącej i sąsiada.
Czas znajdowania sąsiada można zmniejszyć, jeśli zamiast drzewa
ósemkowego zastosujemy równomierny podział kostki otaczającej
scenę. W metodzie tej każdy bok kostki dzieli się na ![]() równych
części, w wyniku czego powstaje
równych
części, w wyniku czego powstaje ![]() ,,podkostek”. Są one
elementami trójwymiarowej tablicy i mają tylko jeden atrybut: wskaźnik do
listy obiektów. Mając współrzędne
,,podkostek”. Są one
elementami trójwymiarowej tablicy i mają tylko jeden atrybut: wskaźnik do
listy obiektów. Mając współrzędne ![]() ,
, ![]() ,
, ![]() dowolnego punktu można
obliczyć indeksy do tablicy w czasie stałym. Program, który korzysta z
tej metody może być znacznie prostszy; dodatkowy zysk, to oszczędność
pamięci (nie trzeba przechowywać wskaźników do poddrzew), choć to
oszczędność pozorna. Opisane uproszczenie ma swoją cenę, którą jest
brak adaptacji. W rezultacie
dowolnego punktu można
obliczyć indeksy do tablicy w czasie stałym. Program, który korzysta z
tej metody może być znacznie prostszy; dodatkowy zysk, to oszczędność
pamięci (nie trzeba przechowywać wskaźników do poddrzew), choć to
oszczędność pozorna. Opisane uproszczenie ma swoją cenę, którą jest
brak adaptacji. W rezultacie
-
zbyt gruby podział może być nieskuteczny (tj. listy obiektów są zbyt długie),
-
zbyt drobny podział powoduje, że większość elementów tablicy zawiera wskaźniki puste (czyli pamięć jest marnowana) i tablica zajmuje dużo miejsca,
-
duże puste obszary są drobno ,,poszatkowane” i czas przechodzenia przez taki obszar jest długotrwały,
-
duże obiekty występują w dużej liczbie list.
W praktyce przyjmuje się ![]() rzędu kilkunastu.
rzędu kilkunastu.
11.3.3. Połączenie śledzenia promieni z 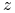 -buforem
-buforem
Większość obiektów w typowych scenach jest matowa, w związku z czym nie
obserwujemy w takich scenach wielokrotnych odbić światła i nawet
zastosowanie algorytmu z ![]() -buforem, połączonego z odpowiednim modelem
oświetlenia daje duży stopień ,,realizmu” obrazu. W takiej sytuacji
można użyć algorytmu z
-buforem, połączonego z odpowiednim modelem
oświetlenia daje duży stopień ,,realizmu” obrazu. W takiej sytuacji
można użyć algorytmu z ![]() -buforem do znacznego przyspieszenia śledzenia
promieni. Metoda jest następująca:
-buforem do znacznego przyspieszenia śledzenia
promieni. Metoda jest następująca:
-
Narysuj scenę za pomocą algorytmu z
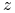 -buforem. Ustaw cieniowanie
płaskie i nadaj każdemu obiektowi (nie uwzględniając
oświetlenia) kolor reprezentowany przez liczbę całkowitą, będącą
numerem obiektu (osobnym obiektem w tym przypadku jest np. każda ściana).
Cieniowanie Gourauda w przypadku, gdy wszystkie wierzchołki wielokąta
mają ten sam kolor, powoduje nadanie tego samego koloru wszystkim
zamalowanym pikselom.
-buforem. Ustaw cieniowanie
płaskie i nadaj każdemu obiektowi (nie uwzględniając
oświetlenia) kolor reprezentowany przez liczbę całkowitą, będącą
numerem obiektu (osobnym obiektem w tym przypadku jest np. każda ściana).
Cieniowanie Gourauda w przypadku, gdy wszystkie wierzchołki wielokąta
mają ten sam kolor, powoduje nadanie tego samego koloru wszystkim
zamalowanym pikselom. -
Kolejno dla każdego piksela na obrazie, odczytaj jego kolor — określa on numer obiektu widocznego w tym pikselu. Z
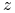 -bufora
odczytaj głębokość i na jej podstawie (oraz na podstawie
współrzędnych
-bufora
odczytaj głębokość i na jej podstawie (oraz na podstawie
współrzędnych 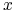 ,
, 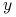 piksela) oblicz współrzędne punktu
przecięcia z obiektem promienia pierwotnego, który odpowiada temu
pikselowi.
piksela) oblicz współrzędne punktu
przecięcia z obiektem promienia pierwotnego, który odpowiada temu
pikselowi.Następnie wykonaj śledzenie promieni wtórnych. Jeśli obiekt jest matowy, to wystarczy zbadać, czy dany punkt jest w cieniu. Jeśli obiekt jest zwierciadlany lub przezroczysty, to rekurencyjne śledzenie promieni jest potrzebne w celu otrzymania obrazu obiektów odbitych lub położonych za tym obiektem.
11.4. Śledzenie promieni i konstrukcyjna geometria brył
Metoda śledzenia promieni może być zastosowana do otrzymania obrazu sceny złożonej z brył CSG, bez wyznaczania jawnej reprezentacji takiej bryły. Wystarczy, aby mając dany promień, wyznaczyć punkt przecięcia (i wektor normalny w tym punkcie) powierzchni prymitywu, która jest brzegiem bryły CSG.
Rozważmy dwie metody. Metoda pierwsza: Wyznaczamy punkty przecięcia promienia z wszystkimi prymitywami bryły CSG i porządkujemy je w kolejności rosnącej odległości od początku promienia. Dla każdego prymitywu jego przecięcie z promieniem składa się z odcinków (dla brył wypukłych jest to najwyżej jeden odcinek). Następnie wykonujemy operacje CSG (tj. regularyzowane działania teoriomnogościowe) na tych odcinkach, co jest bez porównania łatwiejsze niż działania na bryłach trójwymiarowych. Na końcu wystarczy wybrać koniec odcinka najbliżej obserwatora.
Metodę tę można usprawnić; wykonując działania na listach odcinków, jeśli jeden z argumentów różnicy lub przecięcia jest zbiorem pustym, to nie trzeba wyznaczać drugiego argumentu.
Metoda druga: W metodzie pierwszej trzeba wyznaczyć wszystkie punkty przecięcia promienia z wszystkimi prymitywami. Metoda druga opiera się na fakcie, że stosując drzewo ósemkowe (albo równomierny podział kostki), otrzymujemy poszczególne punkty przecięcia promienia i powierzchni obiektów w kolejności zbliżonej do uporządkowania ich wzdłuż promienia. Rozważmy drzewo CSG, w którego liściach umieścimy zamiast prymitywów ich części wspólne z promieniem (tj. sumy odcinków leżących na promieniu). Początkowo wszystkie liście drzewa oznaczamy jako ,,nieznane”. Po wyznaczeniu przecięcia promienia z dowolnym prymitywem, podstawiamy odpowiednie odcinki do drzewa CSG i próbujemy określić wyrażenia, których to są argumenty. Jeśli uda się dojść w ten sposób do korzenia, to znajdziemy w nim punkt najbliżej początku promienia, jak poprzednio.
11.5. Antyaliasing
Zjawisko intermodulacji (ang. alias) jest skutkiem reprezentowania sygnału (w tym przypadku obrazu) za pomocą skończonej liczby próbek. Objawia się ono w postaci
-
,,ząbkowanych” krawędzi obiektów na obrazie,
-
znikania lub zniekształcania małych przedmiotów,
-
zniekształcenia wyglądu tekstur (to jest najbardziej widoczny i najtrudniejszy do przeciwdziałania artefakt),
-
skokowego ruchu i efektów stroboskopowych w animacji.
11.5.1. Antyliasing przestrzenny
Dokładniejszy opis zjawiska intermodulacji i metod radzenia sobie z nim będzie później, a na razie zajmiemy się metodami związanymi ze śledzeniem promieni.
-
Nadpróbkowanie (ang. supersampling). Wykonujemy obraz o
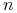 razy większej rozdzielczości (mamy w ten sposób
razy większej rozdzielczości (mamy w ten sposób 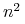 razy
więcej promieni pierwotnych). Barwa przypisywana pikselowi jest średnią
arytmetyczną otrzymanych w ten sposób barw ,,podpikseli”, czyli
pikseli rastra o większej rozdzielczości. W praktyce przyjmuje się
razy
więcej promieni pierwotnych). Barwa przypisywana pikselowi jest średnią
arytmetyczną otrzymanych w ten sposób barw ,,podpikseli”, czyli
pikseli rastra o większej rozdzielczości. W praktyce przyjmuje się
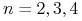 (rzadko więcej).
(rzadko więcej). -
Nadpróbkowanie adaptacyjne. Widoczne na obrazie artefakty zajmują zwykle nie więcej niż pewną małą część powierzchni obrazu (chyba, że dotyczą tekstury). Dlatego często robi się tak:
-
Wykonujemy obraz w niskiej rozdzielczości (jeden promień pierwotny na piksel),
-
Kolejno dla każdego piksela sprawdzamy, czy jego barwa różni się od barw sąsiednich pikseli o więcej niż określony próg. Jeśli tak, to generujemy dodatkowe promienie pierwotne (dla pewnej liczby podpikseli danego piksela) i obliczamy ostateczną barwę jako średnią barw podpikseli. Postępowanie to bywa czasem stosowane rekurencyjnie (tj. jeśli barwy podpikseli za bardzo się różnią, to podpiksele te podlegają dalszemu podziałowi i śledzi się jeszcze więcej promieni pierwotnych).
-
W pewnych sytuacjach nadpróbkowanie adaptacyjne może nie wykryć miejsc, w których należałoby śledzić dodatkowe promienie pierwotne. Często np. szczegóły wyglądu tekstury mogą być mniejsze niż piksel. Nie ma prostego rozwiązania tego problemu, zwłaszcza w przypadku obrazów, w których są widoczne odbicia obiektów w powierzchniach zakrzywionych.
-
Jittering. W przypadku nadpróbkowania artefakty w postaci ,, ząbkowanych” krawędzi obiektów są zastępowane przez mniej widoczne artefakty w postaci brzegu ostrego/nieostrego (okresowo na przemian). Lepsze efekty można osiągnąć zaburzając punkty, które określają kierunki promieni pierwotnych. Zamiast przez środek podpiksela, promień pierwotny jest określony przez wylosowany punkt należący do podpiksela. Takie postępowanie wprowadza do obrazu szum, który dla ludzkich oczu jest znacznie mniej widoczny i denerwujący.
-
Filtrowanie. Oprócz obliczania barwy jako średniej arytmetycznej próbek, można obliczyć średnią ważoną. Średnia taka jest przybliżeniem pewnej całki, która opisuje splot funkcji opisującej obraz z ustaloną funkcją zwaną filtrem. Funkcja taka jest dobierana zależnie od specyfiki urządzenia wyjściowego, np. może być inna dla monitorów z kineskopem i z wyświetlaczem ciekłokrystalicznym. W ogólności mamy dwa wzory; pierwszy opisuje to, co chcemy uzyskać:
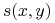
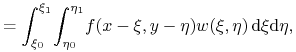
a drugi realizację (zamiast całki obliczamy kwadraturę): 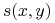
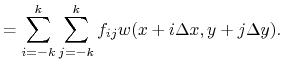
Filtr powinien być funkcją symetryczną, tj. spełniać warunki
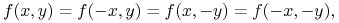
unormowaną (tj.
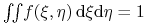 ,
albo
,
albo 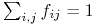 , o jednym maksimum w punkcie
, o jednym maksimum w punkcie 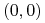 .
.
Na przykład nadpróbkowanie i obliczanie średniej arytmetycznej jest zastosowaniem
filtru prostokątnego. Inne, często stosowane filtry to filtr stożkowy,
Gaussowski i inne. Szczególnie interesujący teoretycznie, choć
rzadko stosowany w praktyce jest filtr opisany przez funkcję sinc (łac. sinus cardinalis), ![]() .
.
11.5.2. Antyaliasing czasowy
Wyświetlanie ciągu obrazów przedstawiających kolejne fazy ruchu daje złudzenie ruchu, co znalazło praktyczne zastosowania co najmniej od czasów braci Lumière.
Zasada działania kamery filmowej jest następująca.
Migawka jest tarczą z wyciętym pewnym segmentem i podczas filmowania
obraca się ze stałą prędkością. W czasie, gdy dowolna część lub
całe okienko o wymiarach klatki jest odsłonięte, film jest nieruchomy (i
następuje naświetlenie klatki). W czasie, gdy okienko jest zasłonięte,
następuje przesuwanie taśmy. Typowy kąt wyciętego segmentu migawki ma od
![]() do
do ![]() , co oznacza, że czas naświetlania (dla
, co oznacza, że czas naświetlania (dla ![]() klatek na sekundę, tak jak w kinie) jest od
klatek na sekundę, tak jak w kinie) jest od ![]() do
do ![]() sekundy.
Jeśli filmowane obiekty poruszają się, to na poszczególnych klatkach są
poruszone, tj. nieostre z wyróżnieniem kierunku ruchu. Gdyby były one
idealnie ostre, to obserwator widziałby serię wyraźnie widocznych
położeń obiektów.
sekundy.
Jeśli filmowane obiekty poruszają się, to na poszczególnych klatkach są
poruszone, tj. nieostre z wyróżnieniem kierunku ruchu. Gdyby były one
idealnie ostre, to obserwator widziałby serię wyraźnie widocznych
położeń obiektów.
Dodatkowy skutek aliasu czasowego to tzw. zjawisko stroboskopowe. Jeśli mamy obiekt obracający się z dużą prędkością (np. śmigło, szprychy koła w dyliżansie), to możemy otrzymać wrażenie ruchu z inną (znacznie mniejszą) prędkością, być może w przeciwną stronę.
Aby otrzymać na klatkach produkowanego przez komputer filmu rozmyte
w kierunku ruchu obrazy obiektów, można dokonać nadpróbkowania i nieraz
tak się robi podczas stosowania algorytmu z ![]() -buforem. Efekt jest jednak
dość marny, po prostu widać (mniej wyraźnie, ale jednak) gęstszy ciąg
(nieco bladych) położeń obiektów. Ponieważ jednak w algorytmie
śledzenia promieni mamy możliwość przetwarzania każdego promienia
osobno, więc możemy stosować jittering czasowy: dla ustalonego promienia
pierwotnego, śledzonego w celu otrzymania klatki filmu w chwili
-buforem. Efekt jest jednak
dość marny, po prostu widać (mniej wyraźnie, ale jednak) gęstszy ciąg
(nieco bladych) położeń obiektów. Ponieważ jednak w algorytmie
śledzenia promieni mamy możliwość przetwarzania każdego promienia
osobno, więc możemy stosować jittering czasowy: dla ustalonego promienia
pierwotnego, śledzonego w celu otrzymania klatki filmu w chwili ![]() ,
losujemy zaburzenie
,
losujemy zaburzenie ![]() , o wartości bezwzględnej mniejszej niż
połowa odstępu czasowego między kolejnymi klatkami. Następnie obliczamy
położenia wszystkich obiektów sceny w czasie
, o wartości bezwzględnej mniejszej niż
połowa odstępu czasowego między kolejnymi klatkami. Następnie obliczamy
położenia wszystkich obiektów sceny w czasie ![]() i obliczamy
wartość próbki (intensywność światła przyniesionego przez promień)
w zwykły sposób. Połączenie tej metody z jitteringiem przestrzennym
pozwala zachować niezbyt dużą liczbę (nie więcej niż kilkanaście)
promieni na piksel. Obrazy bardzo wysokiej jakości wymagają śledzenia do
kilkudziesięciu promieni pierwotnych na piksel.
i obliczamy
wartość próbki (intensywność światła przyniesionego przez promień)
w zwykły sposób. Połączenie tej metody z jitteringiem przestrzennym
pozwala zachować niezbyt dużą liczbę (nie więcej niż kilkanaście)
promieni na piksel. Obrazy bardzo wysokiej jakości wymagają śledzenia do
kilkudziesięciu promieni pierwotnych na piksel.
Aby zmniejszyć koszt obliczeń, można stosować techniki
przyśpieszające, takie jak drzewo ósemkowe. W takiej sytuacji bryła
ograniczająca obiekt musi być otoczką wszystkich położeń obiektu w
pewnym przedziale czasowym (który zawiera chwile ![]() dla
wszystkich wylosowanych zaburzeń
dla
wszystkich wylosowanych zaburzeń ![]() ). Ponieważ liczba obiektów
trafionych przez promień pierwotny i wszystkie jego promienie wtórne jest
zwykle znacznie mniejsza niż liczba wszystkich obiektów, więc opłaca
się stosować ,,leniwe wartościowanie”: położenie obiektu w chwili
). Ponieważ liczba obiektów
trafionych przez promień pierwotny i wszystkie jego promienie wtórne jest
zwykle znacznie mniejsza niż liczba wszystkich obiektów, więc opłaca
się stosować ,,leniwe wartościowanie”: położenie obiektu w chwili
![]() obliczamy po trafieniu przez promień jego bryły otaczającej.
obliczamy po trafieniu przez promień jego bryły otaczającej.
11.6. Symulacja głębi ostrości
Oglądając scenę trójwymiarową, widz skupia uwagę na głównym przedmiocie swojego zainteresowania, nie zwracając uwagi na jego otoczenie i tło. Oko dostosowuje się do odległości od tego przedmiotu, wskutek czego bliższe i dalsze przedmioty są nieostre. Wykonując fotografię, trzeba również odpowiednio nastawić ostrość i nie jest to tylko kwestia niedoskonałości zasady działania obiektywu, ale przede wszystkim świadomego wyboru tematu zdjęcia. Obrazy, na których wszystko byłoby idealnie ostre, są trudniejsze w oglądaniu (i sprawiają nienaturalne wrażenie).
Obraz punktu utworzony przez obiektyw jest plamką o pewnej średnicy, która zależy od długości ogniskowej obiektywu, jego odległości od obiektu i od błony filmowej (albo macierzy CCD) oraz średnicy otworu przysłony. Inne czynniki, które mają na to wpływ (np. dokładne ustawienie soczewek, zjawiska związane z dyfrakcją) pominiemy, przedstawiając obiektyw jako idealną soczewkę, która spełnia równanie
W równaniu tym ![]() oznacza odległość punktu od obiektywu,
oznacza odległość punktu od obiektywu, ![]() to
odległość ostrego obrazu tego punktu od obiektywu (po drugiej jego
stronie), a
to
odległość ostrego obrazu tego punktu od obiektywu (po drugiej jego
stronie), a ![]() jest długością ogniskowej. Średnicę otworu
jest długością ogniskowej. Średnicę otworu ![]() przysłony
najczęściej określa się za pomocą bezwymiarowego współczynnika
przysłony
najczęściej określa się za pomocą bezwymiarowego współczynnika ![]() (z dobrego powodu — gęstość mocy światła padającego na film jest
proporcjonalna do
(z dobrego powodu — gęstość mocy światła padającego na film jest
proporcjonalna do ![]() , a zatem nastawianie przysłony według
światłomierza nie zależy od długości ogniskowej). Na podstawie
schematycznego rysunku łatwo jest wyprowadzić wzór opisujący średnicę
plamki, która jest obrazem punktu:
, a zatem nastawianie przysłony według
światłomierza nie zależy od długości ogniskowej). Na podstawie
schematycznego rysunku łatwo jest wyprowadzić wzór opisujący średnicę
plamki, która jest obrazem punktu:
Mamy dwa sposoby otrzymania obrazu, który charakteryzowałby się głębią
ostrości. Sposób pierwszy polega na postprocesingu; dla każdego piksela
musimy znać odległość punktu powierzchni widocznej w tym pikselu od
obserwatora (przypominam, że położenie obserwatora jest w tym przypadku
tożsame ze środkiem soczewki). Informację taką możemy uzyskać zarówno
jako wynik śledzenia promienia pierwotnego, jak i sięgając do ![]() -bufora.
Znając tę odległość możemy obliczyć średnicę plamki, a następnie
dokonać filtrowania (obliczyć splot), z zastosowaniem filtru
dobranego do obliczonej średnicy plamki. Metoda ta nie najlepiej spisuje
się w pobliżu ostrych krawędzi przedmiotów położonych na znacznie
bardziej oddalonym tle (które musi być bardzo nieostre). Ponadto otrzymany
efekt nie dotyczy obrazów oglądanych w lustrze, a powinien (odległość
przedmiotu od lustra jest istotna i nie należy jej pomijać).
-bufora.
Znając tę odległość możemy obliczyć średnicę plamki, a następnie
dokonać filtrowania (obliczyć splot), z zastosowaniem filtru
dobranego do obliczonej średnicy plamki. Metoda ta nie najlepiej spisuje
się w pobliżu ostrych krawędzi przedmiotów położonych na znacznie
bardziej oddalonym tle (które musi być bardzo nieostre). Ponadto otrzymany
efekt nie dotyczy obrazów oglądanych w lustrze, a powinien (odległość
przedmiotu od lustra jest istotna i nie należy jej pomijać).
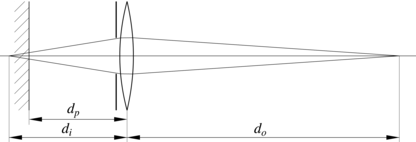
Metoda druga polega na zaburzaniu położenia obserwatora i ,,klatki”,
tj. prostokąta położonego na rzutni, na którym powstaje obraz.
Przypuśćmy, że chcemy ostrość ustawić na odległość ![]() .
W układzie obserwatora przesuniemy w kierunku osi
.
W układzie obserwatora przesuniemy w kierunku osi ![]() (równolegle do
rzutni) obserwatora na odległość
(równolegle do
rzutni) obserwatora na odległość ![]() , a rzutnię na odległość
, a rzutnię na odległość ![]() .
Odległość
.
Odległość ![]() obiektywu od klatki jest równa
obiektywu od klatki jest równa ![]() .
Na podstawie rysunku 11.3 wnioskujemy, że musi być
.
Na podstawie rysunku 11.3 wnioskujemy, że musi być
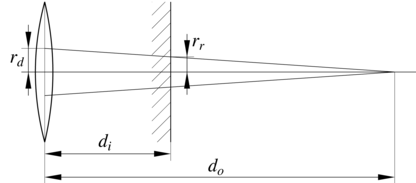
Rozważmy teraz punkt położony w odległości ![]() od obiektywu. Ostry
obraz tego punktu powstanie w odległości
od obiektywu. Ostry
obraz tego punktu powstanie w odległości ![]() od obiektywu. Plamka, która
jest obrazem tego punktu w odległości
od obiektywu. Plamka, która
jest obrazem tego punktu w odległości ![]() , ma średnicę
, ma średnicę
Ponieważ przesunięcie ![]() jest związane ze średnicą plamki wzorem
jest związane ze średnicą plamki wzorem
więc możemy je obliczyć następująco:
Uwaga: Rozpatrując punkt położony w innej odległości niż
![]() otrzymalibyśmy inne przesunięcie
otrzymalibyśmy inne przesunięcie ![]() . Nie ma to wielkiego
znaczenia dla jakości końcowego obrazu.
. Nie ma to wielkiego
znaczenia dla jakości końcowego obrazu.
Przed wykonaniem obrazu ustalamy parametry obiektywu i odległość ostrego
widzenia i na ich podstawie obliczamy maksymalne przesunięcie ![]() środka obiektywu. Podczas śledzenia promieni, generując promień
pierwotny, wybieramy wektor
środka obiektywu. Podczas śledzenia promieni, generując promień
pierwotny, wybieramy wektor ![]() , którego współrzędne
spełniają warunek
, którego współrzędne
spełniają warunek ![]() i mogą być np. wylosowane.
Wektor ten dodajemy do położenia obserwatora
i mogą być np. wylosowane.
Wektor ten dodajemy do położenia obserwatora ![]() , otrzymując
początek
promienia. Iloczyn tego wektora i liczby
, otrzymując
początek
promienia. Iloczyn tego wektora i liczby ![]() dodajemy do
punktu rzutni, przez który przechodziłby promień niezaburzony; otrzymany
punkt wyznacza kierunek promienia. Symulacja głębi ostrości wykonywana w
ten sposób zawsze łączy się z antyaliasingiem, tzn. zaburzamy w ten
sposób promienie, które służą do obliczania próbek obrazu o wyższej
rozdzielczości, filtrowanego następnie w celu otrzymania pikseli obrazu
końcowego.
dodajemy do
punktu rzutni, przez który przechodziłby promień niezaburzony; otrzymany
punkt wyznacza kierunek promienia. Symulacja głębi ostrości wykonywana w
ten sposób zawsze łączy się z antyaliasingiem, tzn. zaburzamy w ten
sposób promienie, które służą do obliczania próbek obrazu o wyższej
rozdzielczości, filtrowanego następnie w celu otrzymania pikseli obrazu
końcowego.
Antyaliasing przestrzenny i czasowy oraz symulacja głębi ostrości są
możliwe do osiągnięcia także na obrazach otrzymanych za pomocą ![]() -bufora.
Służy do tego tzw. bufor akumulacji, który jest tablicą pikseli
o wymiarach takich jak obraz. Aby wykonać obraz antyaliasowany
i z głębią ostrości, trzeba narysować go kilkakrotnie, z położeniem
obserwatora i rzutni zaburzonym zgodnie z podanym wyżej opisem. Odbywa
się to kosztem kilkakrotnego wydłużenia czasu obliczeń.
-bufora.
Służy do tego tzw. bufor akumulacji, który jest tablicą pikseli
o wymiarach takich jak obraz. Aby wykonać obraz antyaliasowany
i z głębią ostrości, trzeba narysować go kilkakrotnie, z położeniem
obserwatora i rzutni zaburzonym zgodnie z podanym wyżej opisem. Odbywa
się to kosztem kilkakrotnego wydłużenia czasu obliczeń.
11.7. Układy cząsteczek
Efekty specjalne, takie jak dym, chmury, płomienie itd. można wymodelować za pomocą układu cząsteczek (ang. particle systems). Często wiąże się to z animacją.
Cząsteczka jest obiektem, który w najprostszym przypadku ma tylko ![]() atrybut: położenie w przestrzeni. Przypuśćmy, że mamy zobrazować dym
unoszący się z komina. W tym celu
atrybut: położenie w przestrzeni. Przypuśćmy, że mamy zobrazować dym
unoszący się z komina. W tym celu
-
Określamy pole wektorowe, które opisuje prędkości unoszenia cząsteczek przez wiatr, ,,cug” z komina itp. W zasadzie takie pole spełnia pewien układ równań różniczkowych cząstkowych, ale często wystarczy wygenerować je ,,ręcznie”.
-
W określonym miejscu (np. wylocie z komina) losujemy położenia początkowe cząsteczek, z określoną szybkością (np. kilkadziesiąt na jedną klatkę filmu).
-
Dalsze położenia cząsteczek obliczamy całkując pole wektorowe unoszenia. Dokładniej, następne położenie cząsteczki otrzymamy, dodając do poprzedniego położenia wektor prędkości unoszenia w tym miejscu razy przyrost czasu (odległość w czasie między wyświetlaniem kolejnych klatek) i przemieszczenie opisujące indywidualny ruch (ruchy Browna, opadanie z powodu grawitacji itd.).
Cząsteczki, które zostały uniesione poza ustalony obszar ,, znikają”. Zwalniamy zajmowane przez nie miejsca w tablicy cząsteczek i możemy w to miejsce wpisać położenia nowych cząsteczek, wylosowane w późniejszych chwilach.
-
Wykonujemy śledzenie promieni. Ponieważ średnica cząsteczek jest równa
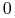 , więc szansa trafienia cząsteczki jest równa
, więc szansa trafienia cząsteczki jest równa 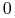 , ale
traktujemy promień jak walec o ustalonym promieniu i liczymy
cząsteczki, które znajdują się w tym walcu między początkiem
promienia i punktem przecięcia promienia z najbliższą powierzchnią.
Każda cząsteczka tłumi (częściowo pochłania) światło. Zależnie
od liczby cząsteczek, które wpadły do walca, korygujemy
intensywność światła niesionego przez promień.
, ale
traktujemy promień jak walec o ustalonym promieniu i liczymy
cząsteczki, które znajdują się w tym walcu między początkiem
promienia i punktem przecięcia promienia z najbliższą powierzchnią.
Każda cząsteczka tłumi (częściowo pochłania) światło. Zależnie
od liczby cząsteczek, które wpadły do walca, korygujemy
intensywność światła niesionego przez promień.Zauważmy, że postępowanie to dla promieni wtórnych pozwala otrzymać obraz cienia rzucanego przez dym na inne przedmioty.
Aby uzyskać zadowalający efekt, zwykle wystarczy symulować ruch od
![]() do
do ![]() tysięcy cząsteczek.
tysięcy cząsteczek.
11.8. Implementacja programu do śledzenia promieni
Program wykonujący obrazy metodą śledzenia promieni11Moje próby zwięzłego spolszczenia określenia “ray tracer” zakończyły się po tym, jak pomyślałem o ,,śledziu promieni”. Mimo poprawności rybnej konotacji (słowo ray oznacza po angielsku również płaszczkę) nie uważam tego pomysłu za udany i więcej prób nie podejmę. może (i powinien) składać się z modułów w znacznym stopniu niezależnych od siebie. Moduły te to
-
Translator reprezentacji sceny. W pakietach ,,użytkowych” moduł ten zawiera procesor tekstu, którego zadaniem jest utworzenie wewnętrznej reprezentacji sceny na podstawie skryptu (dostarczonego przez użytkownika programu). Procesor ten wywołuje procedury konstruujące obiekty reprezentujące poszczególne prymitywy i wierzchołki drzewa lub grafu hierarchii sceny (w tym np. wierzchołki reprezentujące operacje CSG) i buduje ten graf. Ponadto rozpoznaje i odpowiednio przetwarza opisy źródeł światła i położenia obserwatora.
Przed napisaniem translatora należy określić język opisu sceny, tj. pewien język formalny, którego zdaniami są dopuszczalne teksty skryptów. Translator składa się z analizatora leksykalnego (który może być wyposażony w makrogenerator), analizatora syntaktycznego (który rozpoznaje opisy obiektów i np. kojarzy rozpoznane opisy tekstur z rozpoznanymi opisami figur geometrycznych) i generatora obiektów, który tworzy obiekty, nadaje wartości ich atrybutom i buduje z nich drzewo lub graf hierarchii.
Możliwym rozwiązaniem zastępczym jest użycie w charakterze takiego translatora kompilatora języka programowania, w którym realizujemy cały program (np. Pascala, C, C++). Wtedy zamiast skryptu opisującego scenę użytkownik będzie musiał napisać i dołączyć do programu procedurę, która wywołuje (dostępne w postaci biblioteki) odpowiednie procedury konstruujące ,,wewnętrzną” reprezentację sceny. Po wywołaniu tej procedury program może przystąpić do syntezy obrazu.
Zaletą tego rozwiązania jest możliwość wykorzystania dowolnych konstrukcji językowych w celu utworzenia sceny, a także łatwość rozszerzania możliwości programu (np. dodawania nowych rodzajów prymitywów) bez potrzeby zmieniania języka skryptów. Wadą jest przyjęcie założenia, że użytkownik programu umie pisać przynajmniej proste programy i umie obsługiwać kompilator. W praktyce często kompilator pełni rolę translatora reprezentacji sceny podczas uruchamiania modułu syntezy obrazu. Są również gotowe pakiety, które oferują (czasem opcjonalnie) taki interfejs użytkownika.
-
Biblioteka obiektów. Każdy element reprezentacji sceny (np. prymityw lub obiekt złożony) jest obiektem, który powinien udostępniać metody stanowiące interfejs sceny z procedurą śledzenia promieni opisaną dalej. W najprostszym przypadku wystarczą dwie metody. Pierwsza z nich wyznacza punkty przecięcia promienia danego jako parametr z obiektem i wektory normalne powierzchni obiektu w tych punktach. Druga metoda dla ustalonego punktu oblicza wartość tekstury w tym punkcie, czyli parametry (związane z powierzchnią) występujące na przykład w modelu oświetlenia Phonga. Może też być trzecia metoda, której zadaniem jest narysowanie obiektu przy użyciu algorytmu z buforem głębokości, w celu przyspieszenia przetwarzania promieni pierwotnych sposobem opisanym w p. 11.3.3.
Bardzo wygodne jest zrealizowanie tych obiektów w języku ,,obiektowym”, na przykład w C++. Wspomniane metody będą oczywiście wirtualne. W klasie ,,figura” (której obiektami są wszystkie elementy reprezentacji sceny) metody będą puste, natomiast w podklasach będą odpowiednio przedefiniowane. Dzięki temu procedura śledzenia promieni może wywoływać odpowiednią metodę ,,nie wiedząc”, czy należy ona do obiektu opisującego sferę, płat B-sklejany, czy też wewnętrzny wierzchołek drzewa CSG. W ostatnim przypadku obiekt zawiera wskaźniki do poddrzew reprezentujących argumenty operacji CSG; metoda obiektu wywoła metody znajdowania przecięć promienia z tymi argumentami (,,nie wiedząc” jakiego one są rodzaju), a następnie obliczy punkt przecięcia promienia z bryłą CSG na podstawie wyników obliczeń dokonanych przez metody argumentów.
-
Procedura śledzenia promieni. Procedura ta otrzymuje promień jako argument. Jej zadaniem jest znalezienie odpowiedniego punktu przecięcia z którymś z obiektów (w tym celu procedura wywołuje metody obiektów), a następnie wygenerowanie promieni wtórnych, prześledzenie ich (za pomocą rekurencyjnego wywołania) i obliczenie światła niesionego przez promień do jego początku.
Jedynie ta procedura realizuje określony algorytm śledzenia, tj. tylko w niej jest określona liczba generowanych promieni wtórnych i kryterium zatrzymania rekurencyjnych wywołań.
Procedura śledzenia promieni może posługiwać się strukturą danych taką jak drzewo ósemkowe w celu usprawnienia obliczeń. Alternatywnie, zadanie zmniejszania złożoności obliczeniowej wyznaczania przecięć może spoczywać na metodach obiektów, jeśli obiekty te są zorganizowanie hierarchicznie. Na przykład procedura wywołuje metody tylko jednego lub najwyżej kilku obiektów, z których każdy jest korzeniem drzewa opisującego pewną część sceny. Działanie metody znajdowania przecięć promienia z obiektem zaczyna się od sprawdzania położenia promienia względem bryły otaczającej (i najczęściej na tym się kończy).
-
Generator promieni pierwotnych. To jest procedura, która oblicza kolor kolejnych pikseli na obrazie (wywołując procedurę śledzenia promieni), przy czym szczegóły obliczeń takie jak liczba promieni pierwotnych na piksel i rodzaj zastosowanego filtru w antyaliasingu są poza tą procedurą niewidoczne (z jednym wyjątkiem — w antyaliasingu czasowym procedura ta musi nadawać odpowiednie wartości globalnemu parametrowi czasu, na podstawie którego metody obiektów określają położenie tych obiektów w chwili, w której trafia je promień).
-
Biblioteka procedur wyjściowych, których zadaniem jest utworzenie odpowiedniego pliku w ustalonym formacie lub wyświetlenie obrazu na ekranie. Zmiana formatu pliku wymaga dokonania zmian tylko w tym module.