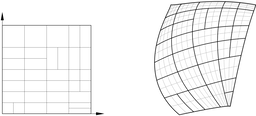Zagadnienia

8.1 Drzewa czwórkowe
8.2 Drzewa ósemkowe
8.3 Drzewa binarne
8.4 Binarny podział przestrzeni

8. Drzewa binarne, czwórkowe i ósemkowe

Wiele zadań związanych z przetwarzaniem figur geometrycznych można rozwiązać lub uprościć dokonując podziału tych figur. Podział może być wykonany w sposób zależny od figury (np. triangulacja wielokąta polega na dzieleniu wzdłuż odcinków, których końcami są wierzchołki wielokąta), albo w sposób arbitralny.

Zajmiemy się teraz rekurencyjnym podziałem kostki $d$ -wymiarowej. Otrzymane fragmenty kostki nazwiemy boksami. Każdy boks powstaje przez podział większego boksu na równe części. Wspólne ściany tych części są równoległe do ścian kostki. Podział taki możemy wykonywać stosownie do potrzeb i stosownie do potrzeb możemy wybierać metodę podziału.

8.1. Drzewa czwórkowe

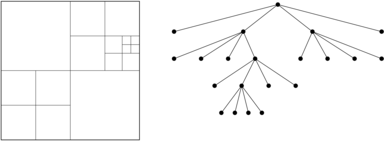
Rys. 8.1. Podział kwadratu na boksy i odpowiadające mu drzewo czwórkowe.

Zaczniemy od przypadku najłatwiejszego do narysowania, a zatem najbardziej odpowiedniego do przedstawienia zasady. Przyjmiemy, że $d=2$ , a zatem kostka jest kwadratem (albo, ogólniej, prostokątem). Cała kostka jest reprezentowana przez korzeń drzewa. Kostkę i każdy boks dzielimy na cztery przystające kwadraty (lub prostokąty). Każdy wierzchołek drzewa, który nie jest liściem, ma cztery poddrzewa.

Drzewa czwórkowe można zastosować w naturalny sposób do rozwiązywania różnych zadań dwuwymiarowych, takich jak

Przeszukiwanie obszarów, na przykład w geograficznej bazie danych,
Konstrukcyjna geometria figur płaskich,
Algorytmy widoczności,
Transmisja obrazów,
Wykrywanie kolizji w ruchu płaskim, np. w animacji.

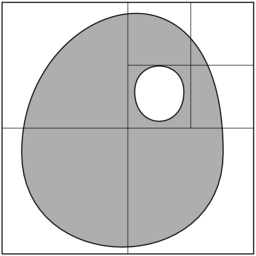
Omówimy reprezentację płaskiej figury $F$ , mieszczącej się w prostokącie. Z każdym wierzchołkiem drzewa zwiążemy atrybut, zwany umownie kolorem. Wierzchołek jest

czarny, jeśli wnętrze boksu reprezentowanego przez ten wierzchołek jest zawarte w figurze $F$ ,
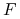biały, jeśli wnętrze boksu jest rozłączne z figurą $F$ ,
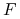szary, jeśli przecięcie wnętrza boksu i brzegu figury 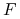$F$ jest niepuste.

Nie ma powodu, aby dzielić wierzchołki czarne i białe, zatem są one zwykle liśćmi drzewa, a wszystkie wierzchołki wewnętrzne są szare. Istnieją też na ogół szare liście, co wynika z ograniczenia wysokości drzewa, które określa osiągalną dokładność reprezentowania figur. Można jednak umieścić w szarych liściach dodatkową informację, która pozwala na przykład zbadać, czy dany punkt, należący do boksu reprezentowanego przez szary liść, należy do $F$ , czy nie. Informacja taka może być prostsza niż reprezentacja całej figury $F$ .

Rys. 8.2. Podział kwadratu na boksy dla pewnego wielokąta krzywoliniowego.

Przykład: Niech figura $F$ będzie wielokątem krzywoliniowym, którego brzeg składa się z kilku krzywych sklejanych. Podział boksów wykonujemy do chwili, gdy w każdym boksie, który zawiera fragment brzegu, fragment taki składa się z co najwyżej dwóch połączonych łuków wielomianowych. Sprawdzenie, czy dany punkt $\bm{p}$ należy do $F$ polega na odnalezieniu w drzewie liścia, który zawiera ten punkt, i jeśli ten liść jest szary, to zbadanie, po której stronie brzegu leży punkt $\bm{p}$ , jest dosyć łatwe.

8.1.1. Konstrukcyjna geometria figur płaskich

Drzewo reprezentujące dopełnienie figury reprezentowanej przez dane drzewo czwórkowe jest bardzo łatwe do otrzymania; wystarczy zamienić kolor każdego wierzchołka na przeciwny (tj. czarny na biały, biały na czarny, i szary na złoty). Przetwarzanie dodatkowej informacji o brzegu (jeśli taka jest) może polegać na zmianie orientacji krzywej brzegowej. Jeśli krzywa ta jest krzywą Béziera, to wystarczy w tym celu ustawić jej punkty kontrolne w odwrotnej kolejności.

Mając drzewa reprezentujące dwie figury płaskie, zawarte w tej samej kostce, możemy skonstruować drzewo, które reprezentuje sumę, przecięcie lub różnicę tych figur. Dysponując procedurą wyznaczającą dopełnienie figury, każdą z tych operacji możemy zrealizować za pomocą np. procedury wyznaczania przecięcia. Procedura ta opiera się na fakcie, że każdy boks może być reprezentowany tylko przez wierzchołki znajdujące się w identycznej pozycji w obu drzewach i w obu drzewach może być podzielony tylko w ten sam sposób.

Dzięki powyższej własności drzew, jest możliwe jednoczesne obejście metodą DFS wierzchołków reprezentujących te same boksy. Przetwarzając wierzchołki, którym odpowiada ten sam boks, procedura sprawdza, czy to liście i bada ich kolory. Zależnie od wyniku tego badania, procedura tworzy wierzchołek drzewa reprezentującego przecięcie i nadaje mu kolor, lub wykonuje działanie takie jak w poniższej tabelce:

$\downarrow 1\quad 2\rightarrow$	czarny liść	biały liść	szary liść	poddrzewo
czarny liść	czarny liść	biały liść	szary liść 2	kopia poddrzewa 2
biały liść	biały liść	biały liść	biały liść	biały liść
szary liść	szary liść 1	biały liść	A	B
poddrzewo	kopia poddrzewa 1	biały liść	B	C

Procedura A: jeśli szare liście zawierają informację, która umożliwia dokładne odtworzenie przecięć boksu z figurami, to należy zbadać, czy te przecięcia są rozłączne. Jeśli tak, to procedura tworzy biały liść. W przeciwnym razie powstaje szary wierzchołek, który może być liściem albo korzeniem poddrzewa, jeśli informacja o brzegu przecięcia jest zbyt skomplikowana, aby można ją było przechowywać w liściu. Jeśli drzewa nie zawierają dodatkowej informacji, to procedura tworzy szary liść (albo biały); kolor tego liścia może być błędny.

Procedura B: jeśli nie ma dodatkowej informacji o przecięciu figur z boksem, to procedura tworzy szary liść. W przeciwnym razie szary liść jednego lub drugiego drzewa jest zamieniany na korzeń poddrzewa (zostaje ono rozbudowane przez dodanie czterech liści reprezentujących ćwiartki boksu); wierzchołki obu drzew, reprezentujące te ćwiartki, są następnie przetwarzane rekurencyjnie, za pomocą procedury C.

Procedura C: oba wierzchołki reprezentujące dany boks są wewnętrzne, mają więc wskaźniki do poddrzew reprezentujących ćwiartki boksu. Ćwiartki te przetwarzamy wywołując rekurencyjnie procedurę wyznaczania przecięcia.

Po wykonaniu działań zgodnie z powyższą tabelką i opisem, należy jeszcze uprościć wynik, jeśli się da. Jeśli wierzchołek reprezentujący przecięcie figur w boksie jest korzeniem poddrzewa i wszystkie jego poddrzewa są białymi (albo czarnymi) liśćmi, to usuwamy je i zamieniamy bieżący wierzchołek na biały (albo czarny) liść.

Przykład zastosowania: Przypuśćmy, że jedna z figur przedstawia obszar zalesiony, a druga obszar zabagniony. Ostoję puszczy (tzw. matecznik) możemy zlokalizować wyznaczając drzewo reprezentujące część wspólną tych obszarów.

8.1.2. Algorytm widoczności

Drzewo czwórkowe ma zastosowanie w następującym algorytmie widoczności (algorytmie Warnocka). Przypuśćmy, że mamy scenę trójwymiarową składającą się z płaskich wielokątów o co najwyżej wspólnych krawędziach. Algorytm jest następujący:

Rzutujemy krawędzie wielokątów na płaszczyznę obrazu; dostajemy zbiór rzutów krawędzi.
Tworzymy drzewo czwórkowe, którego korzeń reprezentuje cały obraz. Boks dzielimy na mniejsze wtedy, gdy jest większy niż jeden piksel, a w jego wnętrzu leży rzut jakiejś krawędzi (jest też wariant: więcej niż jednej krawędzi).
Dla każdego liścia znajdujemy środek boksu i rozstrzygamy widoczność w tym punkcie, tj. znajdujemy ścianę, której przecięcie z półprostą, której rzutem jest ten punkt, jest najbliżej obserwatora. Cały boks wypełniamy kolorem tej ściany. W wariancie dopuszczającym obecność rzutu jednej krawędzi wewnątrz boksu reprezentowanego przez liść widoczność rozstrzygamy w dwóch punktach, leżących po przeciwnych stronach tej krawędzi i nadajemy kolory dwóm wielokątom powstałym z podziału boksu przez tę krawędź. Wariant ten działa szybciej, ponieważ wymaga przeszukiwania drzew o znacznie mniejszej wysokości.

8.1.3. Transmisja obrazów i MIP-mapping

Przypuśćmy, że należy przesłać pewien obraz w ten sposób, aby odbiorca mógł go niezbyt dokładnie wyświetlić po otrzymaniu niewielkiej ilości danych. Może wtedy przerwać transmisję przed końcem jeśli obraz mu się nie podoba i nie chce płacić za przesyłanie całości.

Metoda opisana niżej powoduje pewien wzrost objętości danych (o $1/3$ ), ale ponieważ wiele algorytmów kompresji (bezstratnej) działa ,,po kolei” (tj. odtwarza zakodowany ciąg w kolejności uporządkowania jego elementów), więc to nie jest bardzo ważne.

Tworzymy drzewo pełne, którego liście to piksele, a każdy węzeł wewnętrzny ma kolor o wartości średniej arytmetycznej kolorów korzeni poddrzew (kolor korzenia obliczamy na końcu),
Przesyłamy kolory wierzchołków drzewa w kolejności przeszukiwania drzewa algorytmem BFS, tj. najpierw korzeń, potem jego 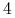$4$ poddrzewa, potem 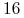$16$ ich poddrzew itd. Wyświetlanie polega na wypełnianiu stałym kolorem coraz mniejszych kwadratów.

Powyższy algorytm, jak łatwo zauważyć, polega na przesyłaniu kolejnych obrazów o rozdzielczości $1\times 1$ , $2\times 2$ itd., aż do oryginalnego obrazu na końcu (z pikselami poprzestawianymi w pewien sposób). Stąd bierze się wspomniany wzrost objętości danych. Zastanówmy się, jak go uniknąć.

Wydawało by się, że znając średnią arytmetyczną czterech liczb i trzy z nich, można obliczyć czwartą, a zatem można by nie przesyłać koloru jednego (np. ostatniego) z czterech poddrzew każdego wierzchołka. Tak jednak nie jest z powodu błędów zaokrągleń. Jeśli jednak zamiast średniej arytmetycznej przyjmiemy kolor korzenia poddrzewa równy kolorowi jednego z wierzchołków jego poddrzew (np. pierwszego), to możemy go później nie przesyłać i błędów zaokrągleń (ani żadnych obliczeń numerycznych) tu nie ma. Jest za to pewne pogorszenie jakości przybliżenia obrazu przez początkowo przesłane dane, przez co decyzja o przesłaniu go do końca lub nie, może być błędna.

Identyczna zasada tworzenia obrazów o niższej rozdzielczości ma zastosowanie w tzw. MIP-mappingu, który jest zastosowaniem elizji w nakładaniu tekstury. Będzie o tym mowa później.

8.2. Drzewa ósemkowe

Drzewa ósemkowe spełniają w zastosowaniu do figur przestrzennych te same role, co drzewa czwórkowe dla figur płaskich. Korzeń drzewa ósemkowego reprezentuje kostkę trójwymiarową (prostopadłościan lub w szczególności sześcian), a jego wierzchołki reprezentują boksy, będące prostopadłościanami podobnymi do całej kostki. Drzewo ósemkowe może być podstawową reprezentacją figury przestrzennej, a także pomocniczą strukturą danych, która ma na celu przyspieszenie pewnych obliczeń.

Przykład: Opisana wcześniej konstrukcyjna geometria brył wielościennych wymaga wyznaczenia wszystkich krawędzi przecięcia ścian danych brył. Jeśli liczby ścian brył oznaczymy symbolami $n_{1}$ i $n_{2}$ , to ,,bezpośrednia” procedura

for i := $1$ to $n_{1}$ do

for j := $1$ to $n_{2}$ do

sprawdź, czy ściany $f_{{1i}}$ i $f_{{2j}}$ przecinają się

i jeśli tak, to wyznacz ich krawędź przecięcia;

ma koszt rzędu $n_{1}n_{2}$ , nawet jeśli liczba znalezionych krawędzi jest znacznie mniejsza. Można jednak dla każdej ściany pierwszej bryły znaleźć kostkę, w której ta ściana jest zawarta, a następnie zbudować drzewo ósemkowe, którego każdy wierzchołek zawiera listę ścian pierwszej bryły, mających niepuste przecięcie z odpowiednim boksem. Następnie, dla każdej ściany drugiej bryły wyszukujemy boksy, z którymi ta ściana przecina się i sprawdzamy, czy istnieją wspólne krawędzie ze ścianami pierwszej bryły znajdującymi się w odpowiednich listach. Ta metoda jest opłacalna zwłaszcza wtedy, gdy brzegi brył składają się z dużej liczby małych ścian.

Kolejne przykłady zastosowania takich drzew, to wykrywanie kolizji obiektów poruszających się w scenie, która nie zmienia się w czasie oraz wyznaczanie przecięć promieni z obiektami w metodzie śledzenia promieni. W obu tych przypadkach oszczędności czasowe mogą być bardzo duże.

8.3. Drzewa binarne

Wadą drzew czwórkowych i ósemkowych może być bardzo duża liczba poddrzew każdego wierzchołka; jeśli liście mają taką samą reprezentację jak wierzchołki wewnętrzne, to mają cztery lub osiem pustych wskaźników.

Druga cecha, która może być zaletą lub wadą (zależnie od sytuacji) to brak adaptacji kierunkowej; na wszystkich poziomach rekurencyjnego podziału boksy są podobne do wyjściowej kostki; nie można w związku z tym dostosować się do ,,wydłużonych” obiektów.

Aby to umożliwić, można zamiast drzewa czwórkowego lub ósemkowego zastosować drzewo binarne, w którym boksy dzieli się na dwie części — prostokąty albo prostopadłościany, i można przy tym dowolnie (na przykład kilka razy kolejno tak samo) wybrać kierunek podziału.

Rys. 8.3. Przykład zastosowania drzewa binarnego.

Przedstawione na rysunku drzewo binarne powstało z zastosowaniem adaptacyjnego wyboru kierunku podziału boksów. Pokazany płat był dzielony rekurencyjnie na kawałki za pomocą algorytmu de Casteljau. Kierunek podziału był za każdym razem wybierany tak, aby otrzymać kawałki o jak najmniejszej średnicy.

8.4. Binarny podział przestrzeni

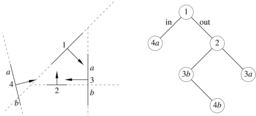
W odróżnieniu od kostki będziemy teraz dzielić całą przestrzeń, czyli zbiór nieograniczony. Idea binarnego podziału przestrzeni (ang. binary space partition, BSP) polega na uzależnieniu go od danych, które wyznaczają pewne hiperpłaszczyzny. Na przykład przestrzeń trójwymiarową będziemy dzielić płaszczyznami, w których leżą dane wielokąty płaskie. Na rysunkach niżej są odcinki, które wyznaczają proste, którymi można podzielić płaszczyznę, bo łatwiej to narysować, a zasada podziału jest identyczna.

Dla każdej ściany znamy jej płaszczyznę, która jest określona przez podanie dowolnego punktu i wektora normalnego. Zwrotu wektora normalego użyjemy do rozróżnienia dwóch półprzestrzeni rozgraniczonych przez ścianę; wektor ten jest zorientowany w stronę półprzestrzeni ,,out”, a druga półprzestrzeń jest oznaczona ,,in”. Dla ścian przetwarzanych w kolejności zgodnej z oznaczeniami na rysunku 8.4 powstanie drzewo przedstawione obok na tym rysunku.

Rys. 8.4. Zasada tworzenia drzewa binarnego podziału przestrzeni.

Korzeń drzewa reprezentuje całą przestrzeń. Po wstawieniu pierwszej ściany mamy dwa poddrzewa, które reprezentują półprzestrzenie. Wstawiając każdą następną ścianę przeszukujemy drzewo algorytmem DFS, wybierając za każdym razem to poddrzewo, które zawiera wstawianą ścianę. Jeśli ściana przecina płaszczyznę podziału przestrzeni, to dzielimy ją na dwie części (np. za pomocą algorytmu Sutherlanda-Hodgmana) i wstawiamy je odpowiednio do lewego i prawego poddrzewa. Ściany położone w płaszczyźnie innej ściany, wstawionej wcześniej, możemy dołączyć do odpowiedniego wierzchołka drzewa (którego atrybutem powinna być wtedy lista ścian).

Zauważmy, że

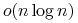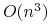Koszt budowy drzewa jest nie mniejszy niż $o(n\log n)$ operacji (jeśli drzewo jest idealnie zrównoważone i żadnej ściany nie trzeba dzielić), i nie większy niż $O(n^{3})$ operacji (ten najgorszy przypadek ma miejsce wtedy, gdy każda ściana przecina się z wszystkimi pozostałymi; wtedy wskutek podziału, niezależnie od uporządkowania otrzymamy 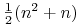$\frac{1}{2}(n^{2}+n)$ fragmentów ścian.).
Jeśli ściany są ścianami wielościanu wypukłego, to drzewo BSP ma wysokość równą liczbie ścian, każdy wierzchołek oprócz ostatniego ma tylko jedno niepuste poddrzewo, a koszt jego utworzenia jest 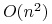$O(n^{2})$ operacji.
Ściany płaskie (wielokąty) można reprezentować za pomocą drzew BSP, które opisują podział płaszczyzn ścian przez proste, na których leżą krawędzie ścian. Można więc wprowadzić hierarchię drzew BSP (i czasem tak się robi).
Budując drzewo BSP warto obniżać jego koszt. Wybierając ścianę, która ma być wstawiona w następnej kolejności, warto wybrać taką ścianę, która
- spowoduje podzielenie najmniejszej liczby pozostałych (jeszcze nie wstawionych) ścian, a najlepiej żadnych,
- rozdzieli pozostałe ściany w przybliżeniu na równoliczne podzbiory (co zmniejsza wysokość drzewa). Aby osiągnąć ten cel, czasem wprowadza się dodatkowe płaszczyzny podziału przestrzeni (bez ścian) — to jest jedyna metoda skuteczna dla zbioru ścian bryły wypukłej.

Drzewa BSP mają zastosowanie w algorytmach widoczności i wyznaczania cieni, a także w różnych zadaniach, w których ich celem jest obniżenie kosztu algorytmu, dzięki zmniejszeniu ilości wykonywanych obliczeń.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Grafika komputerowa I