Zagadnienia
- 11.1 Rodzaje zmienności
- 11.2 Zmienność historyczna
- 11.3 Metody wyznaczania zmienności dziennej
- 11.4 Zmienność implikowana
- 11.5 Uśmiech zmienności
- 11.6 Struktura zmienności implikowanej opcji walutowych
- 11.7 Wyznaczenie zmienności dla opcji o danej cenie wykonania
- 11.8 Zmienność dla opcji dowolnym czasie trwania i cenie wykonania
- 11.9 Struktura zmienności implikowanej opcji na akcje/indeksy
- 11.10 Zmienność lokalna
- 11.11 Zmienność stochastyczna
11. Zmienność
11.1. Rodzaje zmienności
W inżynierii finansowej funkcjonuje wiele rodzajów zmienności. Mamy
-
zmienność historyczną,
-
zmienność implikowaną,
-
zmienność lokalną,
-
zmienność stochastyczną.
Wszystkie one są używane w roli zmienności ![]() , która występuje
w podstawowym modelu opisującym proces cen (w świecie wolnym od
ryzyka)
, która występuje
w podstawowym modelu opisującym proces cen (w świecie wolnym od
ryzyka)
| (11.1) |
gdzie ![]() jest procesem Wienera, a
jest procesem Wienera, a ![]() jest stopą wolną od ryzyka. Zmienność
historyczna jest również używana w niektórych metodach szacowania
ryzyka (rynkowego) portfeli instrumentów finansowych (na przykład w
tak zwanej metodzie delta-normalnej wyznaczania wartości
zagrożonej).
jest stopą wolną od ryzyka. Zmienność
historyczna jest również używana w niektórych metodach szacowania
ryzyka (rynkowego) portfeli instrumentów finansowych (na przykład w
tak zwanej metodzie delta-normalnej wyznaczania wartości
zagrożonej).
Z równania (11.1) wynika, że jeśli ![]() jest
stała, to
jest
stała, to
| (11.2) |
Konsekwencje przyjętego modelu (wzorów (11.1) – (11.2)):
-
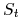 ma rozkład log-normalny, bowiem
ma rozkład log-normalny, bowiem 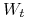 ma rozkład normalny
(o średniej zero i wariancji
ma rozkład normalny
(o średniej zero i wariancji  ),
), -
log-normalność
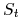 umożliwia wyprowadzenie formuł
Blacka-Scholesa (BS) na wycenę europejskich opcji waniliowych.
umożliwia wyprowadzenie formuł
Blacka-Scholesa (BS) na wycenę europejskich opcji waniliowych.
Uwaga 11.1 (proste uogólnienie modelu Blacka-Scholesa)
Wzór (11.2) zachodzi również w przypadku, gdy ![]() zależy od czasu
zależy od czasu ![]() , ale z małą jego modyfikacją. Mianowicie w
miejsce zmienności
, ale z małą jego modyfikacją. Mianowicie w
miejsce zmienności ![]() należy wstawić we wzorze (11.2)
średnią wartość zmienności na przedziale czasu
należy wstawić we wzorze (11.2)
średnią wartość zmienności na przedziale czasu ![]() :
:
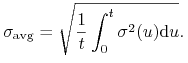 |
W
tym przypadku formuły BS na wycenę opcji pozostają w mocy z
![]() .
.
11.2. Zmienność historyczna
Z (11.2) wynika, że
czyli że ![]() jest zannualizowanym odchyleniem standardowym
(logarytmicznej) stopy zwrotu z
jest zannualizowanym odchyleniem standardowym
(logarytmicznej) stopy zwrotu z ![]() . W związku z tym obliczając cenę
opcji z modelu BS, w określonych przypadkach za
. W związku z tym obliczając cenę
opcji z modelu BS, w określonych przypadkach za ![]() przyjmuje
się wartość obliczoną statystycznym estymatorem odchylenia
standardowego logarytmicznych stóp zwrotu. Tak obliczoną zmienność
nazywamy zmiennością historyczną i na potrzeby naszego wykładu
oznaczamy ją symbolem
przyjmuje
się wartość obliczoną statystycznym estymatorem odchylenia
standardowego logarytmicznych stóp zwrotu. Tak obliczoną zmienność
nazywamy zmiennością historyczną i na potrzeby naszego wykładu
oznaczamy ją symbolem ![]() .
.
Obliczanie zmienności historycznej
Zwykle najpierw oblicza się zmienność w skali jednego dnia
![]() , po czym ta jednodniowa zmienność jest
skalowana do zmienności rocznej wzorem
, po czym ta jednodniowa zmienność jest
skalowana do zmienności rocznej wzorem
| (11.3) |
U w a g i:
-
Magiczna liczba 252 we wzorze (11.3) wynika z założenia, że rok ma 252 dni handlowe. W zasadzie liczba ta zależy od kraju (waluty). W pobieżnych szacunkowych obliczeniach można zmienność dzienną skalować do rocznej mnożąc
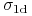 przez 16.
przez 16. -
Skalowanie ,,pierwiastkiem z czasu”, takie jak na przykład w (11.3), jest poprawne pod pewnymi warunkami (szereg czasowy zaobserwowanych wartości
 jest realizacją ciągu niezależnych zmiennych losowych o jednakowym
rozkładzie), które w praktyce rzadko kiedy można uznać, że są
spełnione.
jest realizacją ciągu niezależnych zmiennych losowych o jednakowym
rozkładzie), które w praktyce rzadko kiedy można uznać, że są
spełnione. -
Ze względu na założenia wymienione w punkcie 2, skalowanie ,,pierwiastkiem z czasu” dziennych zmienności wyznaczonych modelami typu GARCH (patrz poniżej) nie ma sensu (bo te modele zakładają, że rozkład zmiennej losowej w danym dniu zależy od rozkładu z poprzedniego dnia!).
11.3. Metody wyznaczania zmienności dziennej
Estymacja zmienności średnią ruchomą (MA)
Załóżmy, że na koniec dnia ![]() dysponujemy szeregiem czasowym
zrealizowanych wartości procesu cen
dysponujemy szeregiem czasowym
zrealizowanych wartości procesu cen
Prognozowana
(estymowana) dzienna wariancja dla następnego dnia ![]() obliczana
jest w następujący sposób:
obliczana
jest w następujący sposób:
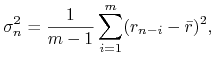 |
(11.4) |
gdzie
| (11.5) |
są zrealizowanymi ,,jednodniowymi” (w okresie od ![]() do
do
![]() ) stopami zwrotu, a
) stopami zwrotu, a
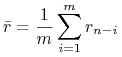 |
(11.6) |
jest estymatorem średniej (wartości oczekiwanej).
Aspekty praktyczne
-
Jak należy wybrać długość szeregu czasowego zrealizowanych cen
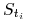 do estymacji zmienności?
do estymacji zmienności?-
a) Czasami
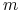 wybiera się tak, by szereg czasowy pokrywał
okres o tej samej długości jak czas trwania opcji. Nie zawsze to ma
sens – w skrajnym przypadku opcji o kilkudniowym czasie trwania
statystyczne własności estymatora obliczonego na podstawie krótkiego
szeregu czasowego są złe.
wybiera się tak, by szereg czasowy pokrywał
okres o tej samej długości jak czas trwania opcji. Nie zawsze to ma
sens – w skrajnym przypadku opcji o kilkudniowym czasie trwania
statystyczne własności estymatora obliczonego na podstawie krótkiego
szeregu czasowego są złe. -
b) Ta uwaga jest adresowana do tych, którzy już wiedzą czym jest wartość zagrożona VaR (Value at Risk) i którzy wcześniej zetknęli się z analizą portfelową. Zmienność historyczną używa się także do obliczania VaR portfela. Mianowicie, w metodzie RiskMetrics obliczania VaR zakłada się, że zmienna losowa opisująca P&L portfela ma rozkład normalny o średniej zero. Wówczas, VaR portfela przy poziomie ufności
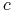 dane jest wzorem
dane jest wzorem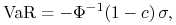
gdzie
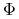 jest dystrybuantą standardowego rozkładu normalnego a
jest dystrybuantą standardowego rozkładu normalnego a
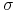 jest odchyleniem standardowym (zmiennością) P&L tego
portfela. Na przykład, przy poziomie ufności
jest odchyleniem standardowym (zmiennością) P&L tego
portfela. Na przykład, przy poziomie ufności 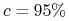 mamy
mamy
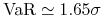 . Zwykle przy obliczaniu odchylenia
standardowego
. Zwykle przy obliczaniu odchylenia
standardowego 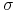 , na jednym z etapów obliczeń, estymowana jest
macierz kowariancji pomiędzy czynnikami ryzyka od których zależy
wartość portfela. Wówczas
, na jednym z etapów obliczeń, estymowana jest
macierz kowariancji pomiędzy czynnikami ryzyka od których zależy
wartość portfela. Wówczas 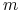 powinno być takie samo dla wszystkich
czynników ryzyka oraz powinno być dostatecznie duże – przy
powinno być takie samo dla wszystkich
czynników ryzyka oraz powinno być dostatecznie duże – przy 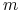 zbyt
małym w stosunku do liczby czynników ryzyka wyestymowana macierz
kowariancji może nie być dodatnio określona.
zbyt
małym w stosunku do liczby czynników ryzyka wyestymowana macierz
kowariancji może nie być dodatnio określona.
-
Estymacja zmienności według EWMA (stosowana przez J.P. Morgan w RiskMetrics)
W tym modelu zakłada się, że
| (11.9) |
gdzie ![]() określa proporcje wkładu (kwadratu) bieżącej
zmiany ceny i (kwadratu) zmienności za poprzedni dzień do bieżącej
wartości (kwadratu) zmienności. Ze wzoru (11.9) wynika, że
określa proporcje wkładu (kwadratu) bieżącej
zmiany ceny i (kwadratu) zmienności za poprzedni dzień do bieżącej
wartości (kwadratu) zmienności. Ze wzoru (11.9) wynika, że
| (11.10) |
Wzór (11.10) wyjaśnia dlaczego model ten nazywa się EWMA (wykładniczo ważona średnia ruchoma) i pokazuje, czym różni się ten sposób estymacji zmienności od estymatora (11.8).
Aspekty praktyczne
-
Wartość parametru
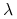 można wyestymować metodą
największej wiarogodności (patrz Hull, 5-th Ed., strony
378–382[1]).
można wyestymować metodą
największej wiarogodności (patrz Hull, 5-th Ed., strony
378–382[1]). -
J.P. Morgan w swoim modelu RiskMetrics przyjmuje
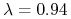 . Według
nich estymatory zmienności obliczone przy tej wartości parametru
. Według
nich estymatory zmienności obliczone przy tej wartości parametru
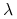 są bliskie zrealizowanej zmienności wyliczonej jako
średnia z 25 kolejnych ,,przyszłych” (w stosunku do dnia estymacji)
wielkości
są bliskie zrealizowanej zmienności wyliczonej jako
średnia z 25 kolejnych ,,przyszłych” (w stosunku do dnia estymacji)
wielkości 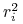 .
.
Estymacja zmienności według GARCH(1,1)
W tym modelu zakłada się, że
| (11.11) |
gdzie
przy czym zwykle zakłada się, że
Wielkość ![]() w (11.11) jest długoterminową średnią
wariancją w tym sensie, że jeżeli
w (11.11) jest długoterminową średnią
wariancją w tym sensie, że jeżeli ![]() , to w średniej
, to w średniej
Gdy ![]() ,
, ![]() ,
, ![]() ,
GARCH(1,1) redukuje się do EWMA.
,
GARCH(1,1) redukuje się do EWMA.
Aspekty praktyczne
-
Wartości parametrów
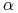 ,
, 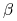 i
i 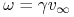 można wyestymować metodą największej wiarogodności.
można wyestymować metodą największej wiarogodności. -
Proces estymacji parametrów można uprość przyjmując za
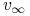 długoterminową średnią obliczoną na przykład wzorem (11.4).
Ustalenie
długoterminową średnią obliczoną na przykład wzorem (11.4).
Ustalenie 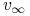 umożliwia wyznaczenie parametru
umożliwia wyznaczenie parametru 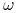 przy
danych
przy
danych 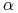 i
i 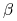 , bowiem
, bowiem 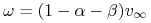 .
.
-
Jeżeli stosujemy model GARCH(1,1) do wyznaczania zmienności, macierz kowariancji powinna być wyznaczana również w analogiczny sposób.
11.4. Zmienność implikowana
-
Formuła Blacka-Scholesa (BS) jest wyprowadzona przy silnych założeniach, o których na ogół możemy z góry powiedzieć, że nie są w rzeczywistości spełnione.
-
Tym niemniej, formuła BS przyjęła się w praktyce, choć jest używana inaczej niż było jej pierwotne przeznaczenie.
-
W uproszczeniu, można powiedzieć, że formuła BS jest narzędziem do ,,interpolacji” rynkowej ceny opcji. Przy tej interpolacji kluczową rolę odgrywa zmienność implikowana.
Przypomnijmy podstawowe oznaczenia:
-
 – bieżąca wartość instrumentu podstawowego,
– bieżąca wartość instrumentu podstawowego, -
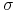 – zmienność,
– zmienność, -
 – cena wykonania,
– cena wykonania, -
 – czas trwania opcji,
– czas trwania opcji, -
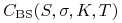 – cena BS waniliowej opcji call,
– cena BS waniliowej opcji call, -
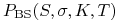 – cena BS waniliowej opcji put,
– cena BS waniliowej opcji put,
-
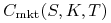 – cena rynkowa waniliowej opcji call,
– cena rynkowa waniliowej opcji call, -
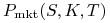 – cena rynkowa waniliowej opcji put.
– cena rynkowa waniliowej opcji put.
Definicja 11.1
Zmienność implikowana (ang. implied volatility)
![]() to liczba, która spełnia równanie
to liczba, która spełnia równanie
| (11.12) |
dla danych ![]() ,
, ![]() ,
, ![]() (zależność od stóp procentowych jest
zaniedbywana).
(zależność od stóp procentowych jest
zaniedbywana).
Jak widać z (11.12),
Sens zmienności implikowanej
![]() kalibruje formułę BS dla opcji o czasie
trwania
kalibruje formułę BS dla opcji o czasie
trwania ![]() i cenie wykonania
i cenie wykonania ![]() do ceny rynkowej. Inaczej,
zmienność implikowana to specjalna liczba, która wstawiona
do niewłaściwej (bo obowiązującej przy założeniach, o
których z góry można powiedzieć, że nie są spełnione) formuły
(Blacka-Scholesa) daje właściwą (prawdziwą, rynkową)
wartość opcji.
do ceny rynkowej. Inaczej,
zmienność implikowana to specjalna liczba, która wstawiona
do niewłaściwej (bo obowiązującej przy założeniach, o
których z góry można powiedzieć, że nie są spełnione) formuły
(Blacka-Scholesa) daje właściwą (prawdziwą, rynkową)
wartość opcji.
Uwagi
-
Ponieważ vega opcji
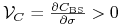 ,
zmienność
,
zmienność 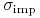 istnieje i jest jednoznaczne
wyznaczona przez (11.12), o ile
istnieje i jest jednoznaczne
wyznaczona przez (11.12), o ile
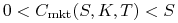 .
. -
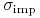 spełnia również równanie
spełnia również równanie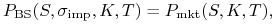
(11.13) bowiem jak wynika z parytetu opcji call-put (który jest spełniony bez żadnych modelowych założeń),
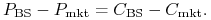
Inaczej: zmienność implikowana ITM (OTM) call jest taka sama jak zmienność OTM (ITM) put.
11.5. Uśmiech zmienności
Terminologia
-
Zależność
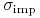 od czasu trwania opcji
od czasu trwania opcji  nazywamy
strukturą terminową zmienności implikowanej (dla ustalonych
nazywamy
strukturą terminową zmienności implikowanej (dla ustalonych  i
i
 ).
). -
Zależność
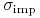 od ceny wykonania
od ceny wykonania  (czy od ilorazu
(czy od ilorazu
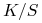 , czy też od ,,delty” opcji) nazywamy uśmiechem zmienności
implikowanej (dla ustalonego
, czy też od ,,delty” opcji) nazywamy uśmiechem zmienności
implikowanej (dla ustalonego  ).
).
Sposób prezentacji uśmiechu zmienności
-
w zależności od ceny wykonania
 – dla opcji na akcje/indeksy,
dla zestawu opcji na stopę procentową (dla cap/floor), dla opcji na
kontrakt IRS (dla swapcji),
– dla opcji na akcje/indeksy,
dla zestawu opcji na stopę procentową (dla cap/floor), dla opcji na
kontrakt IRS (dla swapcji), -
w zależności od ,,delty” (to jest wielkości blisko związanej z deltą opcji) – dla opcji walutowych,
-
w zależności od wielkości
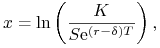
która określa ,,poziom (stopień) bycia w pieniądzu” opcji (ang. log-moneyness) – w rozważaniach teoretycznych. I tak dla
-
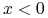 – opcja call (put) jest ITM (OTM),
– opcja call (put) jest ITM (OTM), -
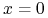 – opcja call (put) jest ATM-F (at the money
forward),
– opcja call (put) jest ATM-F (at the money
forward), -
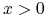 – opcja call (put) jest OTM (ITM).
– opcja call (put) jest OTM (ITM).
-
U w a g i:
-
Czasami
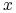 (log-moneyness) jest definiowane ,,z przeciwnym znakiem”.
Jest to kwestia przyjęcia pewnej konwencji.
(log-moneyness) jest definiowane ,,z przeciwnym znakiem”.
Jest to kwestia przyjęcia pewnej konwencji. -
Wyjaśnienia wymaga pojęcie ,,delty” używane do opisu uśmiechu zmienności opcji walutowych. W tym kontekście ,,deltą” jest liczba przeciwna do delty forward opcji put, czyli wielkość
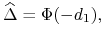
gdzie
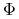 jest dystrybuantą
standardowego rozkładu normalnego. Delta forward to (zwykła) delta
przeniesiona na termin wygaśnięcia opcji czynnikiem
jest dystrybuantą
standardowego rozkładu normalnego. Delta forward to (zwykła) delta
przeniesiona na termin wygaśnięcia opcji czynnikiem 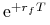 ,
gdzie
,
gdzie 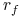 jest stopą waluty bazowej a
jest stopą waluty bazowej a  terminem zapadalności
opcji. W szczególności, na przykład, będziemy mówić o opcji (czy też
zmienności implikowanej) 25-delta put (co oznaczymy symbolem 25P)
mając oczywiście na myśli opcję put (zmienność implikowaną opcji
put), której delta forward wynosi -0.25.
terminem zapadalności
opcji. W szczególności, na przykład, będziemy mówić o opcji (czy też
zmienności implikowanej) 25-delta put (co oznaczymy symbolem 25P)
mając oczywiście na myśli opcję put (zmienność implikowaną opcji
put), której delta forward wynosi -0.25. -
Oś ,,delt” przy prezentacji uśmiechu zmienności bywa różnie oznaczana. Na przykład tak:
-
10P, 25P, ATM, 25C, 10C
lub
-
10P, 25P, 50P, 75P, 90P.
-
Kwotowanie uśmiechu zmienności dla opcji walutowych
W wersji podstawowej uśmiech zmienności jest wyznaczany przez trzy punkty wykresu:
-
zmienność opcji 25-delta put

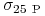 ,
, -
zmienność opcji ATM

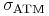 ,
, -
zmienność opcji 25-delta call

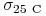 ,
przy czym dwie ostatnie wielkości są kwotowane pośrednio przez
,
przy czym dwie ostatnie wielkości są kwotowane pośrednio przez -
zmienność strategii 25-delta risk reversal (oznaczenie: 25-RR)
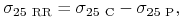
(11.14) -
zmienność strategii 25-delta butterfly (oznaczenie: 25-BF)
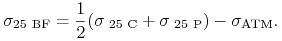
(11.15)
Z tych kwotowań wyliczamy
| (11.16) |
U w a g i:
-
Zmienność strategii 25-delta risk reversal określa stopień ,,skośności” uśmiechu zmienności.
-
Zmienność strategii 25-delta butterfly określa stopień ,,wypukłości” uśmiechu zmienności.
-
Czasami do opisu struktury uśmiechu zmienności używa się również zmienności implikowanych strategii RR i BF przy innych deltach, na przykład 10-delta. Te zmienności, na ogół, nawet jeśli pochodzą z rynku (są kwotowane), są efektem pewnego procesu ,,przybliżania” dokonywanego na podstawie zmienności ATM, 25-RR i 25-BF, przy czym to ,,przybliżanie” może polegać na ocenie rynku przez ,,kwotującego” albo na zastosowaniu pewnych analitycznych metod interpolacji (i ekstrapolacji).
11.6. Struktura zmienności implikowanej opcji walutowych
Dyskretna struktura zmienności implikowanej jest przedstawiona w postaci dwuwymiarowej tablicy, tzn. jako macierz wartości indeksowanych dwiema zmiennymi:
-
okresami, które odpowiadają pewnym ,,wystandaryzowanym” czasom trwania opcji,
-
,,deltami” opcji.
Indeksy czasowe
Standardowo przyjmuje się następujący układ ![]() (
(![]() czasów trwania opcji:
czasów trwania opcji:
1D, 1W, 1M, 2M, 3M, 6M, 9M, 1Y.
Każdego dnia tym okresom są przypisane określone liczby dni odpowiadające czasom trwania opcji, które były by zawarte w danym dniu. Te liczby dni nie są wielkościami stałymi i z dnia na dzień zmieniają się w pewnym zakresie.
Indeksy ,,delta”
Standardowo przyjmuje się następujący układ ![]() (
(![]() ,,delt”, określających stopień ,,bycia w pieniądzu
lub poza pieniądzem” opcji (put):
,,delt”, określających stopień ,,bycia w pieniądzu
lub poza pieniądzem” opcji (put):
0.10, 0.25, 0.50, 0.75, 0.90,
gdzie przypomnijmy znak ujemny delt (forward) opcji put został pominięty.
Dyskretna struktura zmienności implikowanej ma postać następującej tablicy
 |
Przybliżanie zmienności implikowanej względem czasu
W praktyce rynkowej stosuje się jedną z dwóch metod przybliżania zmienności względem czasu trwania opcji, które różnią się sposobem obliczania liczby dni do wygaśnięcia opcji (ang. expiry):
-
metoda podstawowa: uwzględnia się rzeczywistą liczbę dni od daty wyceny (włącznie) do daty wygaśnięcia (wyłącznie),
-
metoda dni handlowych (metoda TD, TD – od ang. Trade Day): przy obliczaniu liczby dni między datą wyceny (włącznie) a datą wygaśnięcia (wyłącznie) dni weekendowe oraz dni świąteczne są uwzględniane z wagami, które mają odzwierciedlić mniejszą zmienność kursu walutowego w tych dniach.
Obliczanie liczby dni w okresie czasu metodą dni handlowych
Niech
-
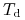 oznacza liczbę dni handlowych w okresie,
oznacza liczbę dni handlowych w okresie, -
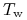 oznacza liczbę dni weekendowych w okresie,
oznacza liczbę dni weekendowych w okresie, -
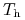 oznacza liczbę dni świątecznych w okresie,
oznacza liczbę dni świątecznych w okresie, -
![\omega _{{\text{w}}}\in[0,1]](wyklady/ifi/mi/mi1483.png) oznacza wagę z jaką
uwzględniane będą dni weekendowe w okresie,
oznacza wagę z jaką
uwzględniane będą dni weekendowe w okresie, -
![\omega _{{\text{h}}}\in[0,1]](wyklady/ifi/mi/mi1517.png) oznacza wagę z jaką
uwzględniane będą dni świąteczne w okresie.
oznacza wagę z jaką
uwzględniane będą dni świąteczne w okresie.
Wówczas liczba dni dla okresu czasu od chwili początkowej (daty
wyceny) do chwili ![]() według metody dni handlowych dana jest wzorem
według metody dni handlowych dana jest wzorem
Załóżmy, że mamy dane wartości ![]() zmienności
implikowanych dla czasów trwania
zmienności
implikowanych dla czasów trwania ![]() ,
, ![]() i przy
których delty opcji (put) wynoszą
i przy
których delty opcji (put) wynoszą ![]() dla pewnego
dla pewnego
![]() . Wartość zmienności implikowanej
. Wartość zmienności implikowanej ![]() opcji (put) z deltą
opcji (put) z deltą ![]() dla czasu trwania:
dla czasu trwania:
-
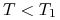 przyjmujemy następująco:
przyjmujemy następująco: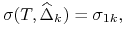
(11.17) -
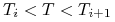 przybliżamy według następującego wzoru
(interpolacja liniowa względem nieannualizowanej wariancji):
przybliżamy według następującego wzoru
(interpolacja liniowa względem nieannualizowanej wariancji):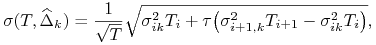
(11.18) gdzie
-
w przypadku metody podstawowej
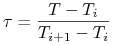
-
w przypadku metody dni handlowych
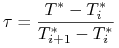
z liczbami dni
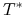 ,
,
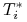 , oraz
, oraz 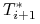 obliczonymi według metody dni handlowych,
obliczonymi według metody dni handlowych,
-
-
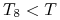 przyjmujemy następująco:
przyjmujemy następująco: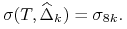
(11.19)
Przybliżenie zmienności względem ,,delt”
Przybliżenia dokonujemy dla ustalonego czasu trwania ![]() , dla
którego mamy dane (lub obliczone stosując przybliżenie zmienności
względem czasu) wartości
, dla
którego mamy dane (lub obliczone stosując przybliżenie zmienności
względem czasu) wartości
![]() zmienności implikowanej dla ,,delt”
zmienności implikowanej dla ,,delt”
![]() (
(![]() ).
).
Przybliżoną wartość zmienności implikowanej
![]()
-
dla czasu trwania
 ,
, -
która odpowiada zadanej wartości ,,delty”
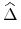 leżącej pomiędzy
leżącej pomiędzy 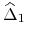 a
a
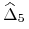
wyznaczamy stosując jedną z dwóch metod:
-
interpolację liniową między punktami
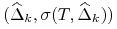 (
(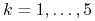 ), to jest
), to jest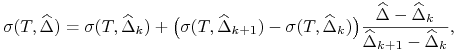
(11.20) jeśli
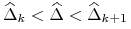 ,
, -
interpolację splajnami, to jest
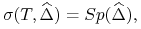
(11.21) gdzie
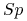 jest
naturalnym splajnem kubicznym wyznaczonym dla układu punktów
jest
naturalnym splajnem kubicznym wyznaczonym dla układu punktów
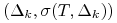 (
(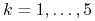 ).
).
Prócz metod interpolacji należy jeszcze określić sposób
ekstrapolacji zmienności, czyli wyznaczania zmienności
![]() w przypadku gdy
w przypadku gdy ![]() lub
lub
![]() . W najprostszym podejściu stosuje się
ekstrapolację stałymi wartościami, to jest:
. W najprostszym podejściu stosuje się
ekstrapolację stałymi wartościami, to jest:
dla ![]() (to jest dla opcji put/call mocno OTM/ITM)
kładziemy
(to jest dla opcji put/call mocno OTM/ITM)
kładziemy
| (11.22) | |||
Uwaga 11.2
Takie rozwiązanie może niedoszacowywać opcje o skrajnych wartościach delt, szczególnie opcje poza pieniądzem.
11.7. Wyznaczenie zmienności dla opcji o danej cenie wykonania
Załóżmy, że mamy dane wartości ![]() zmienności
implikowanej dla ,,delt”
zmienności
implikowanej dla ,,delt” ![]() (
(![]() ) i pewnego
ustalonego czasu trwania
) i pewnego
ustalonego czasu trwania ![]() . Wartość zmienności implikowanej
. Wartość zmienności implikowanej
![]() dla opcji o czasie trwania
dla opcji o czasie trwania ![]() i cenie wykonania
i cenie wykonania ![]() obliczamy następującym iteracyjnym algorytmem.
obliczamy następującym iteracyjnym algorytmem.
Niech
-
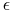 oznacza
zadaną wartość, która określa dokładność z jaką będziemy wyznaczać
zmienność implikowaną.
oznacza
zadaną wartość, która określa dokładność z jaką będziemy wyznaczać
zmienność implikowaną. -
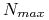 oznacza maksymalną liczbę wykonywanych iteracji.
oznacza maksymalną liczbę wykonywanych iteracji.
Start
-
Kładziemy
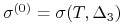 (bierzemy zmienność
implikowaną opcji ATM, czyli takiej której delta forward wynosi 50).
(bierzemy zmienność
implikowaną opcji ATM, czyli takiej której delta forward wynosi 50).
Iteracje
-
Dla
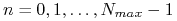 wykonujemy następujące kroki 1-3:
wykonujemy następujące kroki 1-3:-
Obliczamy ,,deltę” opcji ze zmiennością
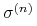 dla
ceny wykonania
dla
ceny wykonania  i czasu trwania
i czasu trwania  :
: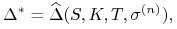
(11.23) gdzie, przypomnijmy,
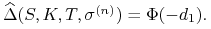
-
Wyznaczamy nową wartość zmienności implikowanej
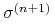 dla opcji z ,,deltą”
dla opcji z ,,deltą” 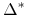 za pomocą jednej z
metod przybliżania względem ,,delty”.
za pomocą jednej z
metod przybliżania względem ,,delty”. -
Jeśli
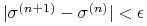 , to iteracje zostają
zatrzymane.
, to iteracje zostają
zatrzymane.
-
Koniec.
Jako wartość zmienności implikowanej dla opcji z ceną wykonania ![]() i czasem trwania
i czasem trwania ![]() przyjmujemy
przyjmujemy
11.8. Zmienność dla opcji dowolnym czasie trwania i cenie wykonania
Wyznaczenie wartości zmienności dla opcji o czasie trwania ![]() i
cenie wykonania
i
cenie wykonania ![]() przebiega w dwóch etapach:
przebiega w dwóch etapach:
Etap 1
Wyznaczamy strukturę ,,uśmiechu” zmienności dla opcji o czasie
trwania ![]() stosując przybliżenie względem czasu.
stosując przybliżenie względem czasu.
Etap 2
Wyznaczamy wartość zmienności dla opcji o czasie trwania ![]() i cenie
wykonania
i cenie
wykonania ![]() stosując schemat iteracyjny względem ,,delt” na
wyznaczonej w Etapie 1 strukturze ,,uśmiechu” zmienności dla opcji
o czasie trwania
stosując schemat iteracyjny względem ,,delt” na
wyznaczonej w Etapie 1 strukturze ,,uśmiechu” zmienności dla opcji
o czasie trwania ![]() .
.
Tak wyznaczona zmienność jest następnie używana do obliczenia wartości opcji waniliowej z modelu BS.
11.9. Struktura zmienności implikowanej opcji na akcje/indeksy
Podobnie jak poprzednio dyskretna struktura zmienności implikowanej jest przedstawiona w postaci dwuwymiarowej tablicy
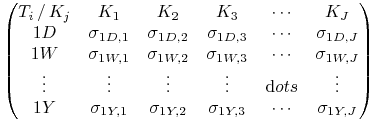 |
indeksowanej dwiema zmiennymi:
-
okresami, które odpowiadają pewnym ,,wystandaryzowanym” czasom trwania opcji,
-
cenami wykonania opcji
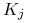 .
.
Wśród cen wykonania ![]() jest cena wykonania opcji ATM, która
zwykle znajduje się w środku ciągu cen
jest cena wykonania opcji ATM, która
zwykle znajduje się w środku ciągu cen ![]() .
.
Wyznaczenie wartości zmienności dla opcji o czasie trwania ![]() i
cenie wykonania
i
cenie wykonania ![]() przebiega podobnie jak poprzednio w dwóch
etapach:
przebiega podobnie jak poprzednio w dwóch
etapach:
Etap 1 jest identyczny jak w przypadku opcji walutowych:
Dla każdej z cen wykonania ![]() wyznaczamy strukturę ,,uśmiechu”
zmienności dla opcji o czasie trwania
wyznaczamy strukturę ,,uśmiechu”
zmienności dla opcji o czasie trwania ![]() stosując przybliżenie
względem czasu, czyli znajdujemy zmienności
stosując przybliżenie
względem czasu, czyli znajdujemy zmienności
![]() .
.
Etap 2 jest prostszy, niż w przypadku opcji walutowych:
Wartość zmienności dla opcji o czasie trwania ![]() i cenie wykonania
i cenie wykonania
![]() wyznaczamy stosując interpolację (liniową / splajnami) lub
ekstrapolację względem zmiennej
wyznaczamy stosując interpolację (liniową / splajnami) lub
ekstrapolację względem zmiennej ![]() na wyznaczonej w Etapie 1
strukturze ,,uśmiechu” zmienności
na wyznaczonej w Etapie 1
strukturze ,,uśmiechu” zmienności ![]() (
(![]() ).
).
Do czego używamy zmienności implikowanych?
-
Do wyceny (z modelu BS) opcji waniliowych.
-
Nie ma uzasadnienia (poza brakiem lepszego pomysłu) dla bezpośredniego używania zmienności implikowanych przy wycenie opcji egzotycznych, bo z definicji zmienności implikowane są skalibrowane tylko do opcji waniliowych. Za teoretyczną cenę opcji egzotycznych przyjmuje się cenę uzyskaną z odpowiedniego modelu BS obliczoną przy zmienności ATM opcji waniliowej.
-
Współczynniki wrażliwości opcji (szczególnie delta) nie powinny być obliczane z wzorów analitycznych wynikających z formuł BS, bowiem w tych wzorach zakłada się że parametr
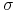 nie zależy od
nie zależy od  . Na
przykład w przypadku obliczania delty, teoretycznie powinniśmy to
zrobić w następujący sposób
. Na
przykład w przypadku obliczania delty, teoretycznie powinniśmy to
zrobić w następujący sposób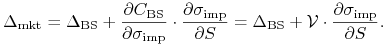
(11.24) Problem polega na tym, że na ogół nie znamy postaci funkcji
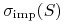 i nie umiemy policzyć analitycznie jej
pochodnej. Zwykle ratujemy się w ten sposób, że obliczamy deltę jako
symetryczny iloraz różnicowy
i nie umiemy policzyć analitycznie jej
pochodnej. Zwykle ratujemy się w ten sposób, że obliczamy deltę jako
symetryczny iloraz różnicowy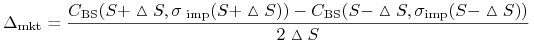
(11.25) dla odpowiednio małej wielkości
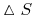 , o ile dysponujemy
metodą (numeryczną), która umożliwia modelowanie uśmiechu zmienności
jako funkcji od ceny bieżącej.
, o ile dysponujemy
metodą (numeryczną), która umożliwia modelowanie uśmiechu zmienności
jako funkcji od ceny bieżącej. -
Płaszczyzna zmienności jest używana jako ,,input” do zbudowania modelu wyceny opcji egzotycznych spójnej z wyceną opcji waniliowych. W tych modelach wprowadza się nowe rodzaje zmienności:
-
lokalną (Derman-Kani),
-
stochastyczną (Hull-White, Heston),
-
kombinację powyższych (model zaimplementowany w J.P. Morgan).
-
Cechy charakterystyczne uśmiechów zmienności
![]() Dla opcji walutowych
Dla opcji walutowych
(a) Dla par walutowych z rozwiniętych rynków
-
Ma symetryczny kształt z ramionami skierowanymi ku górze.
(b) Dla par walutowych, w których jedna waluta jest walutą rozwiniętego rynku, a druga jest walutą wschodzącego rynku
W tym przypadku spotyka się ,,sprzeczne” opinie i obserwacje:
-
Ma często kształt podobny do uśmiechu zmienności, który jest obserwowany dla opcji na akcje?
-
Kształt uśmiechu zmienności podlega częstym zmianom?
![]() Dla opcji na akcje (indeksy)
Dla opcji na akcje (indeksy)
-
Uśmiech zmienności ma zwykle wyraźną skośność.
-
Zmienność maleje wraz ze wzrostem ceny wykonania.
-
Kształt uśmiechu jest bardziej wyraźny dla opcji o krótkim czasie trwania. Dla opcji o dłuższym czasie trwania uśmiech zmienności jest ,,płytki”.
11.10. Zmienność lokalna
Zmienność lokalna to deterministyczna (niestochastyczna) funkcja
![]() , która występuje w równaniu opisującym proces
, która występuje w równaniu opisującym proces
![]() cen instrumentu podstawowego
cen instrumentu podstawowego
| (11.26) |
Uwagi
-
Jeśli
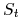 spełnia (11.26), to na ogół (po za kilkoma szczególnymi przypadkami)
nie umiemy podać analitycznego rozwiązania na
spełnia (11.26), to na ogół (po za kilkoma szczególnymi przypadkami)
nie umiemy podać analitycznego rozwiązania na 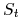 i w związku z
tym nie mamy wzorów będących odpowiednikami formuł BS.
i w związku z
tym nie mamy wzorów będących odpowiednikami formuł BS. -
Natomiast możemy wciąż powiedzieć, że cena instrumentu pochodnego wystawionego na
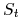 , spełnia równanie Blacka-Scholesa
, spełnia równanie Blacka-Scholesa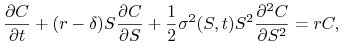
(11.27) które możemy próbować rozwiązywać numerycznie
-
po ,,wyspecyfikowaniu” funkcji
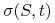 w sposób
zgodny z rynkiem,
w sposób
zgodny z rynkiem, -
po postawieniu warunków brzegowych, które ,,specyfikują” instrument pochodny.
Zwykle nie rozwiązujemy równania (11.27) bezpośrednio, a raczej przekształcamy je tak, by otrzymać inne równanie na inną funkcję (przez którą
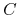 się wyraża), które się łatwiej rozwiązuje.
się wyraża), które się łatwiej rozwiązuje. -
-
Teoretycznie jeśli znamy (z rynku) zależność ceny opcji waniliowych od
 i
i  możemy wyznaczyć funkcję
możemy wyznaczyć funkcję 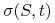 przez przejście do
równania dualnego do (11.27) – tzw. równania
Fokkera-Plancka. Z tego równania wyznaczamy zmienność lokalną w
następujący sposób
przez przejście do
równania dualnego do (11.27) – tzw. równania
Fokkera-Plancka. Z tego równania wyznaczamy zmienność lokalną w
następujący sposób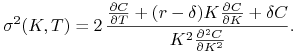
W praktyce są z tym problemy, bo mamy zbyt mało danych z rynku, by w sposób dostatecznie dobry wyliczyć pochodne
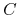 po
po  i
i  , które
występują w równaniu Fokkera-Plancka.
, które
występują w równaniu Fokkera-Plancka. -
Wykres funkcji
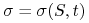 nazywa się płaszczyzną lokalnej
zmienności (nie mylić z płaszczyzną zmienności implikowanej).
nazywa się płaszczyzną lokalnej
zmienności (nie mylić z płaszczyzną zmienności implikowanej).
11.11. Zmienność stochastyczna
Jeśli nie wystarcza nam model (11.26), możemy spróbować skomplikować model jeszcze bardziej, to znaczy założyć że proces cen jest opisany równaniem
| (11.28) |
gdzie tym razem ![]() jest wielkością
stochastyczną, taką, że proces wariancji
jest wielkością
stochastyczną, taką, że proces wariancji
spełnia równanie
| (11.29) |
dla pewnych funkcji ![]() i
i ![]() . Zakłada się również, że procesy
Wienera
. Zakłada się również, że procesy
Wienera ![]() i
i ![]() są skorelowane, w tym sensie, że
są skorelowane, w tym sensie, że
Przykłady modeli dla zmienności
Model Hulla-White'a (1987)
gdzie ![]() ,
, ![]() ,
, ![]() , oraz
, oraz ![]() są stałymi.
są stałymi.
Model Hestona (1993)