Zagadnienia
3. Kontrakt FRA
3.1. Struktura kontraktu FRA
Terminologia:
-
ang. Forward Rate Agreement – FRA,
-
kontrakt na przyszłą stopę procentową.
Oznaczenia
-
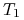 oznacza początek okresu
depozytowego, który jest również datą rozliczenia (ang.
settlement date),
oznacza początek okresu
depozytowego, który jest również datą rozliczenia (ang.
settlement date), -
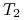 oznacza koniec okresu depozytowego,
oznacza koniec okresu depozytowego, -
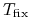 oznacza datę ustalenia stopy referencyjnej (ang. fixing date)
– to jest, zwykle dwa dni robocze przed początkiem okresu
depozytowego,
oznacza datę ustalenia stopy referencyjnej (ang. fixing date)
– to jest, zwykle dwa dni robocze przed początkiem okresu
depozytowego, -
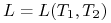 oznacza wartość stopy referencyjnej
zaobserwowaną na rynku w dniu ustalenia stopy - najczęściej są to 1,
3 lub 6 miesięczne stopy lokat/depozytów na rynku międzybankowym –
stopy WIBOR lub LIBOR,
oznacza wartość stopy referencyjnej
zaobserwowaną na rynku w dniu ustalenia stopy - najczęściej są to 1,
3 lub 6 miesięczne stopy lokat/depozytów na rynku międzybankowym –
stopy WIBOR lub LIBOR, -
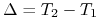 oznacza długość okresu
depozytowego kontraktu FRA obliczoną według właściwej dla danej
waluty konwencji (ACT/360 dla USD, EUR; ACT/365 dla PLN, GBP),
oznacza długość okresu
depozytowego kontraktu FRA obliczoną według właściwej dla danej
waluty konwencji (ACT/360 dla USD, EUR; ACT/365 dla PLN, GBP), -
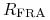 oznacza stopę kontraktu FRA, to
jest zakontraktowaną wysokość stopy procentowej, tzw. cena kontraktu
FRA,
oznacza stopę kontraktu FRA, to
jest zakontraktowaną wysokość stopy procentowej, tzw. cena kontraktu
FRA, -
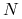 oznacza nominał kontraktu,
oznacza nominał kontraktu, -
Symbole używane na rynku do oznaczania kontraktu: FRA
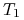 x
x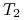 lub FRA
lub FRA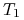 v
v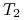 (na przykład: FRA6x9, gdzie ,,6”
odpowiada
(na przykład: FRA6x9, gdzie ,,6”
odpowiada 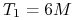 (6 miesięcy od dnia spot), a ,,9” to
(6 miesięcy od dnia spot), a ,,9” to 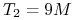 ).
).
Kwota rozliczenia (wypłata z kontraktu FRA) od strony nabywcy kontraktu, znana od momentu ustalenia stopy referencyjnej, płatna w dacie rozliczenia, wynosi
| (3.1) |
Warto zauważyć, że kwota rozliczenia (3.1) nie jest liniową
funkcją stopy ![]() , choć ta nieliniowość nie jest silna bowiem
wartości iloczynu
, choć ta nieliniowość nie jest silna bowiem
wartości iloczynu ![]() są zwykle małe w stosunku do 1.
są zwykle małe w stosunku do 1.
W sensie ekonomicznym (w sensie wartości bieżącej na chwilę ![]() )
wartość kwoty rozliczenia (3.1) kontraktu FRA płatnej w
chwili
)
wartość kwoty rozliczenia (3.1) kontraktu FRA płatnej w
chwili ![]() jest równoważna wartości rozliczenia wymiany w
następującej w chwili
jest równoważna wartości rozliczenia wymiany w
następującej w chwili ![]() odsetek liczonych według stopy zmiennej
odsetek liczonych według stopy zmiennej
![]() na odsetki liczone według stopy kontraktu
na odsetki liczone według stopy kontraktu
![]() , czyli kwoty
, czyli kwoty
| (3.2) |
Strony kontraktów FRA
-
Kupno FRA (długi FRA, ang. long FRA) – kupno pieniędzy (pożyczenie pieniędzy) – płacenie odsetek – płacenie stopy kontraktu FRA
-
Sprzedaż FRA (krótki FRA, ang. short FRA) – sprzedaż pieniędzy (ulokowanie pieniędzy) – otrzymywanie odsetek – otrzymywanie stopy kontraktu FRA
Rola kontraktów FRA
-
Nabywca kontraktu FRA zapewnia sobie określoną w umowie wysokość referencyjnej stopy procentowej, po której będzie mógł się finansować (pożyczyć pieniądze) przez ustalony w kontrakcie przyszły okres czasu.
-
Sprzedawca kontraktu FRA zapewnia sobie możliwość ulokowania po stopie kontraktu FRA swoich funduszy na ustalony w kontrakcie okres czasu.
Jak to działa? Wyjaśnimy to od strony kupującego kontrakt FRA.
-
Zawieramy kontrakt FRA w którym będziemy płacić ustaloną kontraktem stopę
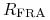 (tzn. kupujemy kontrakt FRA ze stopą
(tzn. kupujemy kontrakt FRA ze stopą
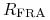 ). Zawarcie kontraktu nic nas nie kosztuje.
). Zawarcie kontraktu nic nas nie kosztuje. -
W chwili
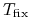 zostaje ustalona wartość
zostaje ustalona wartość 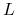 stopy rynkowej na
okres od
stopy rynkowej na
okres od 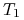 do
do 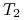 . Przypuśćmy, że
. Przypuśćmy, że 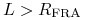 . To
oznacza, że od sprzedawcy kontraktu otrzymujemy kwotę
. To
oznacza, że od sprzedawcy kontraktu otrzymujemy kwotę 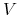 określoną
w (3.1). Wówczas
określoną
w (3.1). Wówczas-
kwotę
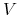 lokujemy po stopie
lokujemy po stopie 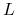 na okres od
na okres od 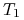 do
do 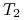 , oraz
, oraz -
kwotę
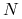 pożyczamy po stopie
pożyczamy po stopie 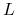 na ten sam okres.
na ten sam okres.
-
-
W chwili
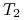
-
z lokaty dostajemy kwotę
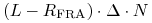 , oraz
, oraz -
zwracamy pożyczony kapitał
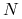 i płacimy należne odsetki w
wysokości
i płacimy należne odsetki w
wysokości  .
.
W efekcie, po zbilansowaniu płatności, od pożyczonego kapitału płacimy odsetki po stopie
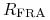 . Gdy
. Gdy 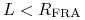 ,
musimy wypłacić sprzedawcy kwotę
,
musimy wypłacić sprzedawcy kwotę 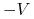 , którą w tym celu pożyczamy na
rynku po stopie
, którą w tym celu pożyczamy na
rynku po stopie 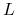 . Wtedy w
. Wtedy w 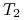 oddajemy kwotę
oddajemy kwotę
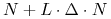 oraz kwotę
oraz kwotę
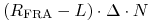 , co znów daje nam efekt taki
sam, jak w poprzednim przypadku.
, co znów daje nam efekt taki
sam, jak w poprzednim przypadku. -
Kontrakty FRA mogą być i są używane przez spekulantów. Spekulant, który przypuszcza, że stopy procentowe w przyszłości
-
wzrosną – kupuje kontrakt FRA,
-
spadną – sprzedaje kontrakt FRA,
bowiem jeśli spełnią się jego spekulacje, to zgodnie ze wzorem (3.1) zyska.
3.2. Wartość kontraktu FRA
(długiej pozycji FRA, kupiony FRA)
-
(a) Wartość zapadłego kontraktu FRA – wartość w dacie lub po dacie ustalenia stopy referencyjnej (
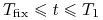 )
)Wartość kontraktu FRA jest równa wartości zdyskontowanej do momentu wyceny ustalonej kwoty rozliczenia (3.1)
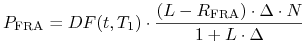
(3.3) -
(b) Wartość kontraktu przed datą ustalenia stopy referencyjnej (
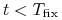 )
)Pokażemy, że wartość w chwili
 niezapadłego kontraktu FRA wynosi
niezapadłego kontraktu FRA wynosi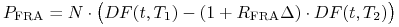
(3.4) W tym celu rozpatrzmy następującą strategię inwestycyjną, która w sposób statyczny replikuje wymianę odsetek
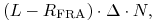
która (hipotetycznie) będzie miała miejsce w chwili
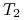 i która ekonomicznie jest
równoważna kwocie rozliczenia kontraktu FRA. Ta strategia polega na
i która ekonomicznie jest
równoważna kwocie rozliczenia kontraktu FRA. Ta strategia polega na-
sprzedaży w chwili
 obligacji zerokuponowej zapadalnej w chwili
obligacji zerokuponowej zapadalnej w chwili 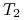 o nominale
o nominale
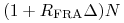 ,
, -
kupnie w chwili
 obligacji zerokuponowej zapadalnej w chwili
obligacji zerokuponowej zapadalnej w chwili 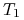 o nominale
o nominale 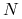 ,
, -
zainwestowaniu w chwili
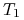 kwoty
kwoty 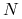 (otrzymanej z zapadającej w
(otrzymanej z zapadającej w 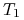 obligacji zerokuponowej)
na okres czasu od
obligacji zerokuponowej)
na okres czasu od 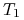 do
do 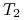 w lokatę oprocentowaną według
rynkowej stopy
w lokatę oprocentowaną według
rynkowej stopy 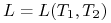 .
.
Jak łatwo sprawdzić, wartość tej strategii w chwili
 dana jest
wzorem
dana jest
wzorem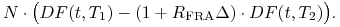
Ponieważ ta strategia replikuje kwotę (hipotetycznego) rozliczenia w
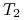 równoważnego rzeczywistemu rozliczeniu kontraktu FRA w chwili
równoważnego rzeczywistemu rozliczeniu kontraktu FRA w chwili
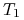 , to z prawa jednej ceny wynika, iż musi zachodzić równość
(3.4).
, to z prawa jednej ceny wynika, iż musi zachodzić równość
(3.4). -
3.3. Stopa kontraktu FRA
W dniu zawarcia kontraktu (ang. trade date) wartość kontraktu
wynosi zero. Niech ![]() oznacza chwilę zawarcia kontraktu. Stopa
oznacza chwilę zawarcia kontraktu. Stopa
![]() z jaką kontrakt został zawarty musiała być taka, by
z jaką kontrakt został zawarty musiała być taka, by
czyli stopa ta powinna była wynosić
| (3.5) |
Jak widać ze wzoru (3.5), w dniu zawarcia kontraktu (w dniu
bieżącym ![]() ) stopa kontraktu FRA jest równa stopie forward dla
okresu depozytowego kontraktu FRA obserwowanej w chwili
) stopa kontraktu FRA jest równa stopie forward dla
okresu depozytowego kontraktu FRA obserwowanej w chwili ![]()
| (3.6) |
gdzie, przypomnijmy, stopa ![]() spełnia warunek
spełnia warunek
| (3.7) |
Inne uzasadnienie równości (3.6). Kupiony kontrakt FRA
pozwala na ustalenie stopy procentowej po której będziemy mogli
pożyczać pieniądze na okres czasu od ![]() do
do ![]() . Z drugiej
strony ten sam efekt możemy uzyskać wykonując w chwili
. Z drugiej
strony ten sam efekt możemy uzyskać wykonując w chwili ![]() dwie
transakcje: pożyczenie pieniędzy na okres czasu od
dwie
transakcje: pożyczenie pieniędzy na okres czasu od ![]() do
do ![]() (sprzedaż obligacji zero-kuponowej o czasie zapadalności
(sprzedaż obligacji zero-kuponowej o czasie zapadalności ![]() ) oraz
jednoczesne ulokowanie tych pieniędzy na okres czasu od
) oraz
jednoczesne ulokowanie tych pieniędzy na okres czasu od ![]() do
do
![]() (kupno obligacji zero-kuponowej o czasie zapadalności
(kupno obligacji zero-kuponowej o czasie zapadalności ![]() ) -
patrz uzasadnienie definicji stopy forward (Wykład 2). Efektem tych
transakcji na obligacjach zero-kuponowych jest zapewnienie sobie
stopy forward
) -
patrz uzasadnienie definicji stopy forward (Wykład 2). Efektem tych
transakcji na obligacjach zero-kuponowych jest zapewnienie sobie
stopy forward ![]() na okres czasu od
na okres czasu od ![]() do
do ![]() przy
zerowych kosztach początkowych. Ekonomicznie transakcja FRA i te
dwie transakcje depozytowe dają ten sam efekt przy tych samych
(zerowych) kosztach. Tak więc, musi zachodzić warunek
(3.6), gdyż w przeciwnym razie moglibyśmy przeprowadzić
transakcję arbitrażową.
przy
zerowych kosztach początkowych. Ekonomicznie transakcja FRA i te
dwie transakcje depozytowe dają ten sam efekt przy tych samych
(zerowych) kosztach. Tak więc, musi zachodzić warunek
(3.6), gdyż w przeciwnym razie moglibyśmy przeprowadzić
transakcję arbitrażową.
Powyższy mechanizm opisany w celu uzasadnienia wzoru (3.6)
przedstawia również sposób replikacji kontraktu FRA przy pomocy
lokaty i depozytu. Kupiony FRA (płacimy stopę FRA) replikujemy
pożyczeniem pieniędzy na okres czasu do chwili ![]() po stopie
po stopie
![]() i ulokowaniem pożyczonych pieniędzy na depozycie do
chwili
i ulokowaniem pożyczonych pieniędzy na depozycie do
chwili ![]() po stopie
po stopie ![]() . W przypadku replikacji
sprzedanego kontraktu FRA postępujemy odwrotnie: pieniądze pożyczamy
na okres do
. W przypadku replikacji
sprzedanego kontraktu FRA postępujemy odwrotnie: pieniądze pożyczamy
na okres do ![]() i robimy depozyt na okres do
i robimy depozyt na okres do ![]() . W tym języku
wzór na stopę kontraktu FRA możemy zapisać następująco
. W tym języku
wzór na stopę kontraktu FRA możemy zapisać następująco
gdzie
![]() jest długością okresu depozytowego, który zaczyna się w
dacie spot dla chwili bieżącej
jest długością okresu depozytowego, który zaczyna się w
dacie spot dla chwili bieżącej ![]() i kończy w
i kończy w ![]() (
(![]() ).
).
3.4. Wyznaczanie wartości kontraktu FRA na podstawie stopy forward
Wartość kontraktu FRA jest równa wartości zdyskontowanej do momentu
wyceny kwoty przyszłego rozliczenia którą, obliczamy wzorem (3.1)
wstawiając w nim zamiast stopy ![]() stopę forward
stopę forward ![]() dla okresu od
dla okresu od ![]() do
do ![]() implikowaną przez strukturę stóp
procentowych z chwili wyceny
implikowaną przez strukturę stóp
procentowych z chwili wyceny ![]()
| (3.8) |
gdzie
| (3.9) |
Dlaczego można tak postąpić? Podamy dwa uzasadnienia.
Otóż w chwili ![]() możemy bez kosztów początkowych zawrzeć kontrakt
FRA na okres od
możemy bez kosztów początkowych zawrzeć kontrakt
FRA na okres od ![]() do
do ![]() zamykający nasz oryginalny
(wyceniany) kontrakt. Stopa tego zamykającego kontraktu FRA jak
wiemy musi wynosić
zamykający nasz oryginalny
(wyceniany) kontrakt. Stopa tego zamykającego kontraktu FRA jak
wiemy musi wynosić ![]() . Ekonomiczny rezultat tego
zamknięcia to wymiana w chwili
. Ekonomiczny rezultat tego
zamknięcia to wymiana w chwili ![]() stopy
stopy ![]() na stopę
na stopę
![]() wycenianego kontraktu FRA. Bieżąca wartość tej
wymiany, która jest de facto wartością oryginalnego kontraktu FRA,
wynosi zatem
wycenianego kontraktu FRA. Bieżąca wartość tej
wymiany, która jest de facto wartością oryginalnego kontraktu FRA,
wynosi zatem
| (3.10) |
Korzystając ze wzoru (3.9) na stopę forward, wyrażenie po prawej stronie równości (3.10) możemy zapisać w postaci (3.8), co uzasadnia tę metodę wyceny kontraktu FRA.
3.5. FRA jako instrument zabezpieczający
Jak widać, kontrakt FRA może służyć do zabezpieczania określonych
płatności odsetkowych. Jeśli mamy otrzymać płatność odsetkową za
przyszły okres czasu od ![]() do
do ![]() zależną od stopy rynkowej
zależną od stopy rynkowej
![]() , która będzie ustalona na ten okres przez rynek, możemy
sprzedać kontrakt FRA na ten okres czasu ze stopą
, która będzie ustalona na ten okres przez rynek, możemy
sprzedać kontrakt FRA na ten okres czasu ze stopą
![]() . W efekcie, możemy uważać, że bez
żadnych kosztów zamieniliśmy nieznaną w chwili
. W efekcie, możemy uważać, że bez
żadnych kosztów zamieniliśmy nieznaną w chwili ![]() stopę rynkową na
stopę
stopę rynkową na
stopę ![]() ustaloną w
ustaloną w ![]() .
.
Wniosek 3.1
Z powyższej analizy wynika, że wyceniając w chwili ![]() (licząc
wartość bieżącą na chwilę
(licząc
wartość bieżącą na chwilę ![]() ) przepływ pieniężny postaci
) przepływ pieniężny postaci
następujący w chwili ![]() (
(![]() jest
stałą niezależną od
jest
stałą niezależną od ![]() ), możemy zastąpić stopę
), możemy zastąpić stopę
![]() stopą forward
stopą forward ![]() . Wtedy wartość w chwili
. Wtedy wartość w chwili
![]() takiego przepływu wynosi
takiego przepływu wynosi
W szczególności, dla
przepływu będącego odsetkami za okres od ![]() do
do ![]()
po skorzystaniu ze wzoru (3.9) na stopę forward, otrzymujemy
3.6. Reprezentacja FRA w postaci strumienia pieniężnego
Jak widać ze wzoru (3.4), wycena kupionego kontraktu FRA jest identyczna jak wycena strumienia pieniężnego
-
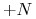 w chwili
w chwili 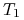 ,
, -
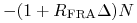 w chwili
w chwili 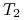 .
.
Podobnie, ze wzoru (3.10) wynika, że wycena kupionego kontraktu FRA jest identyczna jak wycena strumienia pieniężnego
-
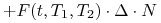 w chwili
w chwili 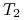 ,
, -
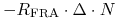 w chwili
w chwili 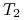 .
.
Uwaga: Powyższe przepływy pieniężne (oraz przepływy pieniężne odpowiadające wzorowi (3.8)) są jedynie przepływami syntetycznymi i w rzeczywistości żadne z tych przepływów nie występują w związku z realizacją kontraktu FRA.
3.7. Aspekty praktyczne
-
Kontrakty FRA są kwotowane ze spreadem kupna – sprzedaży. Cena kupna kontraktu FRA to stopa
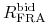 , którą kwotujący jest skłonny
,,płacić” w tym kontrakcie. Analogicznie, cena sprzedaży kontraktu
FRA to stopa
, którą kwotujący jest skłonny
,,płacić” w tym kontrakcie. Analogicznie, cena sprzedaży kontraktu
FRA to stopa 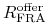 , którą kwotujący jest
gotów ,,otrzymywać” w tym kontrakcie. Jasne, że
, którą kwotujący jest
gotów ,,otrzymywać” w tym kontrakcie. Jasne, że
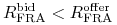 .
. -
Spready kupna – sprzedaży kontraktów FRA są relatywnie małe (kilka lub kilkanaście bp), na ogół dużo mniejsze niż wynikałyby ze spreadów lokat/depozytów replikujących kontrakty FRA (patrz Zadanie 3.1). Jest to związane z różnymi poziomami ryzyka kredytowego w kontraktach FRA i w transakcjach depozytowych. Ponadto, kontrakty FRA, jako transakcje pozabilansowe, mają znacznie większą płynność niż transakcje depozytowe, które wymagają zaangażowania gotówki (są transakcjami bilansowymi).
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 3.1
W dniu 18 października 2004 Bank X kwotował: 3M PLN Depo – 6.65 / 6.85 oraz 6M PLN Depo – 6.80 / 6.95, oraz PLN FRA3x6 – 6.84 / 6.90 (kwotowania na bazie ACT/365). Oblicz ceny kupna / sprzedaży kontraktu FRA3x6, które wynikałyby ze stóp depozytowych. W obliczeniach przyjmij, że okres 3M ma 92 dni a 6M ma 183 dni (od dnia spot).
Ćwiczenie 3.2
Dane są następujące kwotowania rynkowe: FRA3x6 – 5.00%, bon skarbowy o terminie wykupu za 3 miesiące – 98.00, oraz bon skarbowy o terminie wykupu za 6 miesięcy – 97.50. Czy przy tych danych można przeprowadzić arbitraż? W obliczeniach załóż, że okres 3 miesięczny ma 91 dni, a 6 miesięczny 182 dni.
Ćwiczenie 3.3
Dane są dwie obligacje stałokuponowe, które płacą kupon co pół roku:
-
OS1: kupon – 5%, termin zapadalności – za 4 miesiące, cena czysta – 99,58;
-
OS2: kupon – 6%, termin zapadalności – za 7 miesięcy, cena czysta – 100,6.
Stopa procentowa 1M lokat/depozytów wynosi 5,50%. Kwotowanie FRA4x7 wynosi 6,00%. Czy w tej sytuacji jest możliwość przeprowadzenia arbitrażu. Jeśli tak, skonstruuj strategię arbitrażową i oblicz wartość zysku uzyskanego tą strategią.
Ćwiczenie 3.4 (Trochę bardziej skomplikowany wariant poprzedniego zadania.)
Dane są dwie obligacje stałokuponowe, które płacą kupon co pół roku:
-
OS1: kupon – 6.00%, termin zapadalności – za 7 miesięcy, cena czysta – 100.50;
-
OS2: kupon – 6.60%, termin zapadalności – za 10 miesięcy, cena czysta – 100.57.
Stopy procentowe lokat/depozytów wynoszą: 1M – 5.50%, 4M – 5.75%. Kwotowanie kontraktu FRA7x10 wynosi 6.00%. Czy w tej sytuacji jest możliwość przeprowadzenia arbitrażu. Jeśli tak, skonstruuj i opisz strategię arbitrażową. Jaka jest wysokość zysku uzyskanego tym arbitrażem?
Ćwiczenie 3.5
Dwa miesiące temu sprzedaliśmy kontrakt FRA3x6 na nominał 10 mln PLN ze stopą 6.10%. W chwili obecnej kontrakt FRA1x4 ma kwotowanie 5.90/6.05, a WIBOR 1M wynosi 5.80%. Oblicz wartość naszego kontraktu.
Ćwiczenie 3.6
(a) Oblicz BPV kontaktów FRA 3x6, 3x9.
(b) Zbadaj jak BPV kontraktów FRA zmienia się wraz z upływem czasu pozostałego do wygaśnięcia (rozliczenia) kontraktu.
Ćwiczenie 3.7
Pokaż, że ![]() dla nowo zawartego kontraktu (przy przesunięciu równoległym
stóp procentowych w dół o 1 bp).
dla nowo zawartego kontraktu (przy przesunięciu równoległym
stóp procentowych w dół o 1 bp).
Ćwiczenie 3.8
Wycena obligacji o zmiennym kuponie – ang. FRN – Floating Rate Note
Obligacja o zmiennym kuponie płaci kupony, które są obliczane według pewnej referencyjnej rynkowej stopy procentowej (zwykle stopy typu LIBOR).
-
(a) Obligacja o stałym nominale
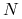 .
.Kupon za okres odsetkowy
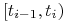 płatny w chwili
płatny w chwili 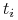 wynosi
wynosi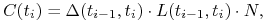
gdzie
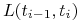 jest stopą rynkową, której wartość jest
ustalana na rynku na początku okresu odsetkowego (w rzeczywistości,
zwykle na dwa robocze przez rozpoczęciem tego okresu). Oblicz
jest stopą rynkową, której wartość jest
ustalana na rynku na początku okresu odsetkowego (w rzeczywistości,
zwykle na dwa robocze przez rozpoczęciem tego okresu). Oblicz-
(i) wartość tej obligacji w chwili
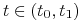 oraz jej
cenę czystą,
oraz jej
cenę czystą, -
(ii) wartość tej obligacji na początku okresu odsetkowego, tj. w chwili
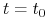 .
.
-
-
(b) Obligacja z amortyzowanym nominałem.
Nominał obligacji zmienia się w trakcie jej trwania według z góry określonego harmonogramu. Niech
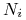 oznacza nominał obligacji w
okresie odsetkowym
oznacza nominał obligacji w
okresie odsetkowym 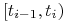 . Kupon za okres odsetkowy
. Kupon za okres odsetkowy
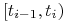 płatny w chwili
płatny w chwili 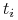 wynosi
wynosi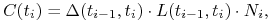
przy oznaczeniach takich samych jak w punkcie (a). Prócz tego kuponu, w chwili
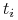 , gdzie
, gdzie 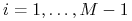 , obligacja zwraca część
nominału odpowiadającą amortyzacji
, obligacja zwraca część
nominału odpowiadającą amortyzacji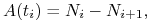
przy czym w terminie wykupu obligacji
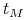 następuje wypłata pozostałej po
tych amortyzacjach ostatniej części
następuje wypłata pozostałej po
tych amortyzacjach ostatniej części 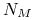 nominału. Oblicz
nominału. Oblicz-
(i) wartość tej obligacji w chwili
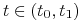 oraz jej
cenę czystą,
oraz jej
cenę czystą, -
(ii) wartość tej obligacji na początku okresu odsetkowego, tj. w chwili
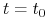 .
.
-
Ćwiczenie 3.9
Obligacja z kapitalizowanymi odsetkami o zmiennym oprocentowaniu.
Jest to obligacja, która zamiast płacić odsetki kapitalizuje je co
okres odsetkowy, przy czym odsetki są obliczane według rynkowej
stopy procentowej ![]() ustalanej przed rozpoczęciem
każdego kolejnego okresu odsetkowego
ustalanej przed rozpoczęciem
każdego kolejnego okresu odsetkowego ![]() , gdzie
, gdzie
![]() . W terminie wykupu
. W terminie wykupu ![]() obligacja zwraca nominał
wraz ze skapitalizowanymi odsetkami, czyli kwotę
obligacja zwraca nominał
wraz ze skapitalizowanymi odsetkami, czyli kwotę
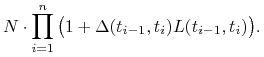 |
Oblicz wartość tej
obligacji w chwili ![]() , gdzie
, gdzie ![]() .
.
Wyceniając tę obligację możesz zastąpić przyszłe w stosunku do
chwili wyceny ![]() stopy
stopy ![]() stopami forward
stopami forward
![]() obserwowanymi w
obserwowanymi w ![]() . Dlaczego możemy tak
postąpić? Pomyśl o serii odpowiednich kontraktów FRA, które musiał
byś zawrzeć w chwili
. Dlaczego możemy tak
postąpić? Pomyśl o serii odpowiednich kontraktów FRA, które musiał
byś zawrzeć w chwili ![]() by uzasadnić podstawienie w miejsce stóp
przyszłych
by uzasadnić podstawienie w miejsce stóp
przyszłych ![]() bieżących stóp forward
bieżących stóp forward
![]() .
.
Ćwiczenie 3.10
Ile wynoszą duracje obligacji opisanych w Ćwiczeniu 3.8 i Ćwiczeniu 3.9?
Ćwiczenie 3.11
Rozważmy dwie obligacje.
-
Obligacja A: płaci stały kupon 8%, płatny co pół roku, termin wykupu przypada za 2 lata i 3 miesiące. Cena czysta tej obligacji wynosi 98, a jej duracja jest równa 1.25.
-
Obligacja B: płaci kupon liczony według 6M stopy rynkowej, płatny co pół roku, termin wykupu przypada za 7 lat i 3 miesiące. Stopa procentowa dla bieżącego okresu odsetkowego została ustalona w wysokości 6%. Cena czysta tej obligacji wynosi 99.
Oblicz o ile procent (w przybliżeniu) zmieni się (a) cena brudna, (b) cena czysta każdej z tych obligacji, jeżeli stopy procentowe zmienią się o +50 bp (punktów bazowych, 1 bp=0.01%). Załóż że stopy są wyrażone na bazie 30/360.




