Zagadnienia
- 6.1 Kontrakty opcyjne
- 6.2 Opcje waniliowe
- 6.3 Opcje egzotyczne
- 6.4 Własności opcji waniliowych
- 6.5 Parytet opcji kupna/sprzedaży
- 6.6 Ograniczenia na wartość opcji
- 6.7 Wczesne wykonanie w opcjach amerykańskich
- 6.8 Zależność wartości opcji europejskiej od ceny wykonania
- 6.9 Zależność wartości opcji europejskiej od ceny instrumentu podstawowego
- 6.10 Wartość czasowa opcji
- Zagadnienia i zadania na Ćwiczenia
6. Kontrakty opcyjne
6.1. Kontrakty opcyjne
Kontrakt opcyjny (krótko: opcja) to umowa na podstawie której
-
jedna strona umowy (posiadacz opcji) nabywa prawo do zrealizowania opisanej umową transakcji lub do otrzymania określonej wypłaty, zaś
-
druga strona (wystawca opcji, sprzedawca opcji) zobowiązuje się być stroną tej transakcji lub, odpowiednio, wypłacić posiadaczowi określoną kwotę.
Posiadacz kontraktu (który zajmuje tzw. długą pozycję) będzie realizował kontrakt tylko wtedy, gdy jest to dla niego korzystne lub otrzyma od wystawcy odpowiednią wypłatę jeśli tylko wypłata ta jest dodatnią wartością. Z tego względu strony kontraktu opcyjnego nie są ,,symetryczne”, w tym sensie, że posiadacz opcji w chwili realizacji opcji z pewnością nie poniesie straty, a wystawca opcji z pewnością nie będzie miał zysku. Z tego powodu wystawca opcji otrzymuje od nabywcy opcji tzw. premię, czyli opłatę, która ma zrekompensować wystawcy jego potencjalnie gorszą sytuację.
Dwa podstawowe problemy związane z kontraktami opcyjnymi są następujące:
-
jaka jest ,,sprawiedliwa” wartość opcji, w szczególności ile powinna wynosić premia opcji,
-
jak wystawca może zabezpieczać swoją pozycję wynikającą ze sprzedanej opcji.
Umowa opcji określa
-
termin wygaśnięcia opcji
 ,
, -
rodzaj transakcji, która będzie wykonywana w przypadku realizacji opcji, lub formułę, według której oblicza się wypłatę opcji; w szczególności wyspecyfikowany jest tzw. instrument podstawowy (ang. underlying) od wartości którego zależy wartość transakcji lub wypłaty opcji,
-
termin lub terminy w których opcja może być realizowana.
Ze względu na instrument podstawowy opcji wyróżniamy w szczególności
-
opcje na akcje,
-
opcje na indeks (giełdowy),
-
opcje walutowe (FX options, currency options) – instrumentem podstawowym jest kurs walutowy,
-
opcje na obligacje (bond options),
-
opcje na kontrakty Futures (Futures options),
-
opcje na stopy procentowe, a wśród nich
-
opcje na poziom stopy procentowej – cap (seria caplet-ów, tj. pojedynczych opcji na górny poziom stopy procentowej) oraz floor (seria floorlet-ów, tj. pojedynczych opcji na dolny poziom stopy procentowej),
-
opcje na kontrakt IRS – swapcje (swaptions).
-
Ze względu na terminy realizacji opcji wyróżniamy
-
opcje europejskie – realizacja opcji może nastąpić tylko w terminie wygaśnięcia opcji,
-
opcje amerykańskie – realizacja opcji może nastąpić w dowolnym momencie przed terminem wygaśnięcia lub w terminie wygaśnięcia opcji,
-
opcje bermudzkie – realizacja opcji może nastąpić w kilku ustalonych chwilach czasu w trakcie trwania opcji.
Niech
-
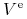 oznacza premię (wartość) opcji europejskiej,
oznacza premię (wartość) opcji europejskiej, -
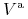 oznacza premię (wartość) opcji amerykańskiej,
oznacza premię (wartość) opcji amerykańskiej, -
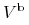 oznacza premię (wartość) opcji bermudzkiej.
oznacza premię (wartość) opcji bermudzkiej.
Wówczas, dla opcji o tym samym terminie wygaśnięcia i o takim samym profilu wypłaty zachodzi
6.2. Opcje waniliowe
Opcja waniliowa (ang. plain vanilla option) jest kontraktem
opcyjnym, w którym przedmiotem umowy opcji jest transakcja
kupna/sprzedaży pewnego aktywa (instrumentu podstawowego) po
ustalonej umową cenie wykonania ![]() :
:
-
opcja kupna (ang. call) – posiadacz opcji ma prawo do kupna aktywa po cenie
 ,
, -
opcja sprzedaży (ang. put) – posiadacz opcji ma prawo do sprzedaży aktywa po cenie
 .
.
Wówczas, wartości tych opcji w chwili ich realizacji ![]() , od strony
posiadacza opcji, wynoszą odpowiednio
, od strony
posiadacza opcji, wynoszą odpowiednio
-
dla opcji kupna:
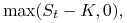
-
dla opcji sprzedaży:
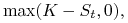
gdzie ![]() jest ceną aktywa w chwili realizacji opcji.
jest ceną aktywa w chwili realizacji opcji.
6.3. Opcje egzotyczne
Modyfikacje opcji waniliowych doprowadziły do skonstruowania szeregu kontraktów opcyjnych o specyficznych właściwościach – opcji egzotycznych (ang. exotic options). Najważniejsze z nich to
-
opcje azjatyckie – opcje w których zamiast ceny
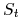 aktywa w chwili realizacji
aktywa w chwili realizacji  opcji do wyznaczenia kwoty wypłaty
(rozliczenia) brana jest
opcji do wyznaczenia kwoty wypłaty
(rozliczenia) brana jest 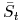 – pewna średnia wartość cen
aktywa, na przykład:
– pewna średnia wartość cen
aktywa, na przykład:-
dyskretna średnia arytmetyczna:
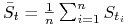 , gdzie
, gdzie
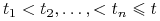 są ustalonymi chwilami czasu w których
obserwowana jest wartość instrumentu podstawowego (przypadek
najczęściej występujący w praktyce),
są ustalonymi chwilami czasu w których
obserwowana jest wartość instrumentu podstawowego (przypadek
najczęściej występujący w praktyce), -
ciągła średnia arytmetyczna:
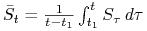 – graniczny przypadek dyskretnej średniej arytmetycznej,
– graniczny przypadek dyskretnej średniej arytmetycznej, -
dyskretna średnia geometryczna:
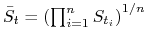 (ma bardziej
znaczenie teoretyczne niż praktyczne),
(ma bardziej
znaczenie teoretyczne niż praktyczne), -
ciągła średnia geometryczna:
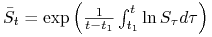 .
.
-
-
opcje lookback – opcje w których zamiast ceny
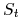 aktywa w chwili realizacji
aktywa w chwili realizacji  opcji do wyznaczenia kwoty
rozliczenia brana jest wartość
opcji do wyznaczenia kwoty
rozliczenia brana jest wartość ![\max\{ S_{t}:t\in[t_{1},t]\}](wyklady/ifi/mi/mi709.png) lub
lub
![\min\{ S_{t}:t\in[t_{1},t]\}](wyklady/ifi/mi/mi718.png) , przy czym podobnie jak dla opcji
azjatyckich możemy mieć warianty ciągłe i dyskretne.
, przy czym podobnie jak dla opcji
azjatyckich możemy mieć warianty ciągłe i dyskretne. -
opcje barierowe – opcje waniliowe z dodatkowym warunkiem uzależniającym wypłatę od tego czy w ustalonym przedziale czasu (zwykle w trakcie całego czasu trwania opcji) cena instrumentu podstawowego ,,dotknie” ustalonej w kontrakcie bariery
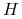 ; opcje
te występują w dwóch (komplementarnych) rodzajach:
; opcje
te występują w dwóch (komplementarnych) rodzajach:-
opcje deaktywujące (ang. knock-out option) – dotknięcie bariery wygasza opcję waniliową,
-
opcje aktywujące (ang. knock-in option) – dotknięcie bariery powoduje uaktywnienie opcji waniliowej,
-
-
opcje binarne typu Cash-or-Nothing – opcje, których wypłata wynosi
-
dla opcji kupna:
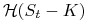 ,
, -
dla opcji sprzedaży:
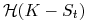 ,
,
gdzie
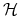 jest funkcją Heaviside'a.
jest funkcją Heaviside'a. -
-
opcje binarne typu Asset-or-Nothing – opcje, których wypłata wynosi
-
dla opcji kupna:
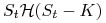 ,
, -
dla opcji sprzedaży:
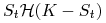 .
.
-
-
jest jeszcze wiele innych rodzajów opcji egzotycznych – patrz np. podręcznik Hull'a.
6.4. Własności opcji waniliowych
Wprowadźmy następującą notację:
-
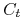 – wartość opcji kupna (call) w chwili
– wartość opcji kupna (call) w chwili  ,
, -
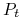 – wartość opcji sprzedaży (put) w chwili
– wartość opcji sprzedaży (put) w chwili  ,
,
przy czym ![]() jest momentem zawarcia opcji.
jest momentem zawarcia opcji.
Typ wykonania opcji będziemy zaznaczać odpowiednim górnym indeksem: e – dla opcji europejskiej, a – dla opcji amerykańskiej, b – dla opcji bermudzkiej.
Zauważmy, że wartości opcji waniliowych spełniają następujące oczywiste ograniczenia:
przy czym dla europejskiej opcji sprzedaży mamy lepsze oszacowanie
gdzie ![]() jest czynnikiem dyskontowym dla waluty w której
wyrażona jest cena aktywa (i cena wykonania
jest czynnikiem dyskontowym dla waluty w której
wyrażona jest cena aktywa (i cena wykonania ![]() ), który odpowiada
wolnej od ryzyka stopy procentowej (tj. odzwierciedlającej czysty
koszt pieniądza w czasie).
), który odpowiada
wolnej od ryzyka stopy procentowej (tj. odzwierciedlającej czysty
koszt pieniądza w czasie).
6.5. Parytet opcji kupna/sprzedaży
![]() Parytet dla opcji europejskich których
instrument podstawowy nie przynosi dochodu
Parytet dla opcji europejskich których
instrument podstawowy nie przynosi dochodu
Twierdzenie 6.1
Wartości europejskich opcji kupna/sprzedaży, w przypadku instrumentu podstawowego, który w trakcie trwania opcji nie przynosi dochodu, spełniają następujący związek, zwany parytetem opcji kupna/sprzedaży,
| (6.1) |
Rozpatrzmy następującą strategię (portfel):
-
kupno opcji kupna z ceną wykonania
 ,
, -
sprzedaż opcji sprzedaży z ceną wykonania
 ,
, -
lokata kwoty
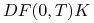 na czas trwania opcji po stopie
wolnej od ryzyka.
na czas trwania opcji po stopie
wolnej od ryzyka.
Koszt tej strategii w chwili jej zawiązania (w ![]() ) wynosi
) wynosi
Natomiast w chwili ![]() wynik naszej strategii będzie następujący:
wynik naszej strategii będzie następujący:
(a) w przypadku gdy ![]() :
:
-
z kupionej opcji kupna:
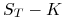
-
ze sprzedanej opcji sprzedaży: 0
-
zwrot z lokaty:

razem otrzymamy ![]() ;
;
b) w przypadku gdy ![]() :
:
-
z kupionej opcji kupna: 0
-
ze sprzedanej opcji sprzedaży:
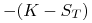
-
zwrot z lokaty:

razem znów otrzymamy ![]() .
.
Tak więc, niezależnie od sytuacji na rynku, w chwili ![]() nasza
strategia przyniesie dochód równy
nasza
strategia przyniesie dochód równy ![]() . Aby nie było możliwości do
przeprowadzenia arbitrażu początkowy koszt tej strategii musi być
równy cenie aktywa w chwili początkowej, czyli musi zachodzić
. Aby nie było możliwości do
przeprowadzenia arbitrażu początkowy koszt tej strategii musi być
równy cenie aktywa w chwili początkowej, czyli musi zachodzić
co kończy uzasadnienie.
∎![]() Parytet dla opcji europejskich których
instrument podstawowy daje ,,dyskretny” dochód.
Parytet dla opcji europejskich których
instrument podstawowy daje ,,dyskretny” dochód.
Twierdzenie 6.2
Parytet opcji kupna/sprzedaży, w przypadku instrumentu podstawowego,
który w trakcie trwania opcji przynosi dochód ![]() płatny w
kilku ustalonych chwilach czasu
płatny w
kilku ustalonych chwilach czasu ![]() ,
, ![]() , ma
następującą postać
, ma
następującą postać
| (6.2) |
gdzie ![]() jest wartością bieżącą
strumienia dochodów generowanych przez aktywo w trakcie trwania
opcji.
jest wartością bieżącą
strumienia dochodów generowanych przez aktywo w trakcie trwania
opcji.
Patrz Ćwiczenia – Zadanie 6.1.
∎![]() Parytet dla opcji europejskich których
instrument podstawowy daje ,,ciągły” dochód.
Parytet dla opcji europejskich których
instrument podstawowy daje ,,ciągły” dochód.
Twierdzenie 6.3
Parytet opcji kupna/sprzedaży, w przypadku instrumentu podstawowego,
który w trakcie trwania opcji przynosi dochód płatny w sposób ciągły
ze stopą ![]() , ma następującą postać
, ma następującą postać
| (6.3) |
Stwierdzenie 6.1
W przypadku opcji amerykańskich różnicę wartości opcji kupna i opcji sprzedaży możemy jedynie oszacować w następujący sposób:
| (6.4) |
gdy instrument podstawowy generuje ,,dyskretne” dochody i wtedy
![]() jest wartością bieżącą tych dochodów (patrz Ćwiczenia –
Zadanie 6.2). Gdy aktywo generuje ,,ciągły” strumień dochodu płatny
ze stopą
jest wartością bieżącą tych dochodów (patrz Ćwiczenia –
Zadanie 6.2). Gdy aktywo generuje ,,ciągły” strumień dochodu płatny
ze stopą ![]() , oszacowanie to przyjmuje następującą postać
, oszacowanie to przyjmuje następującą postać
| (6.5) |
6.6. Ograniczenia na wartość opcji
W poniższym Twierdzeniu zebrane są nierówności na wartość opcji których instrument podstawowy daje ,,dyskretny” dochód.
Twierdzenie 6.4
Wartości opcji spełniają następujące nierówności:
Dla opcji europejskich
| (6.6) |
| (6.7) |
Dla opcji amerykańskich
| (6.8) |
| (6.9) |
Nierówności (6.6), (6.7) dla opcji europejskich wynikają z nieujemności wartości opcji i parytetu opcji kupna/sprzedaży (6.2). Ograniczenia dolne w (6.8), (6.9) dla opcji amerykańskich wynikają w części z odpowiednich nierówności dla opcji europejskich i relacji między wartością opcji amerykańskiej a wartością opcji europejskiej, oraz w pozostałej części z charakteru tych opcji (opcje amerykańskie można w każdej chwili wykonać).
∎6.7. Wczesne wykonanie w opcjach amerykańskich
Twierdzenie 6.5
Jeżeli aktywo, które jest instrumentem podstawowym waniliowej opcji amerykańskiej, nie daje dochodu w trakcie trwania opcji, to wczesne wykonanie opcji kupna nie jest optymalne.
Rozważmy dwie strategie w chwili ![]() :
:
-
Wczesne wykonanie opcji
-
Trzymanie opcji do terminu zapadnięcia opcji
Zbadamy jaki jest rezultat obu strategii w ![]() (w chwili wygaśnięcia
opcji).
(w chwili wygaśnięcia
opcji).
Aby przeprowadzić wczesne wykonanie opcji, pożyczamy kwotę ![]() i za
te pieniądze kupujemy aktywo. W chwili
i za
te pieniądze kupujemy aktywo. W chwili ![]() mamy aktywo warte
mamy aktywo warte ![]() oraz zobowiązanie (dług) w kwocie
oraz zobowiązanie (dług) w kwocie ![]() , czyli ta
strategia ma wartość
, czyli ta
strategia ma wartość
Trzymanie opcji do chwili ![]() : wartość opcji w chwili
: wartość opcji w chwili ![]() wynosi
wynosi
Przy założeniu, że stopy procentowe są dodatnie, czyli gdy
![]() , mamy
, mamy
co oznacza iż bardziej opłaca się trzymać taką opcję do terminu wygaśnięcia opcji niż skorzystać możliwości wczesnego wykonania opcji.
∎Wniosek 6.1
Jeżeli aktywo nie daje dochodu w trakcie trwania opcji, to amerykańska opcja kupna jest równoważna europejskiej opcji kupna i wartości tych opcji są takie same.
Uwaga 6.2
Dla amerykańskiej opcji kupna zachodzi następujące oszacowanie
gdzie ![]() jest dowolną chwilą czasu w trakcie trwania opcji. Warunek
ten oznacza, że chcąc zrealizować wynik na inwestycji w opcję w
chwili
jest dowolną chwilą czasu w trakcie trwania opcji. Warunek
ten oznacza, że chcąc zrealizować wynik na inwestycji w opcję w
chwili ![]() przed terminem wykupu, bardziej opłaca się sprzedać
posiadaną opcję niż ją wykonać i natychmiast sprzedać aktywo po
cenie
przed terminem wykupu, bardziej opłaca się sprzedać
posiadaną opcję niż ją wykonać i natychmiast sprzedać aktywo po
cenie ![]() .
.
Uwaga 6.3
Gdy instrument podstawowy generuje dochód w trakcie trwania opcji
amerykańskiej wcześniejsze wykonanie opcji może być korzystne. Na
przykład rozpatrzmy amerykańską opcję kupna na akcję, która płaci
dywidendę. Niech cena wykonania wynosi ![]() . Przypuśćmy, że
akcja, która kosztuje
. Przypuśćmy, że
akcja, która kosztuje ![]() , wypłaci dywidendę w wysokości
, wypłaci dywidendę w wysokości ![]() w chwili dostatecznie bliskiej terminowi wygaśnięcia opcji. Przed
wypłatą dywidendy opcję możemy zrealizować z zyskiem. Natomiast po
wypłacie dywidendy, kiedy cena akcji spadnie do 95, opcja staje się
bezwartościowa.
w chwili dostatecznie bliskiej terminowi wygaśnięcia opcji. Przed
wypłatą dywidendy opcję możemy zrealizować z zyskiem. Natomiast po
wypłacie dywidendy, kiedy cena akcji spadnie do 95, opcja staje się
bezwartościowa.
Uwaga 6.4
W przypadku amerykańskiej opcji sprzedaży wcześniejsze wykonanie
opcji, nawet dla instrumentów, które nie generują dochodu w trakcie
trwania opcji, może być opłacalne. Na przykład, tak będzie gdy
![]() (dlaczego?).
(dlaczego?).
6.8. Zależność wartości opcji europejskiej od ceny wykonania
Mamy następujące
Twierdzenie 6.6
Rozpatrzmy opcje europejskie na ten sam instrument podstawowy o
ustalonym czasie trwania ![]() . Niech
. Niech ![]()
![]() oznacza cenę opcji kupna (sprzedaży) przy cenie
wykonania
oznacza cenę opcji kupna (sprzedaży) przy cenie
wykonania ![]() dla ustalonej wartości instrumentu podstawowego.
dla ustalonej wartości instrumentu podstawowego.
-
(a) Funkcja
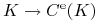
-
jest malejąca,
-
spełnia warunek Lipschitza ze stałą
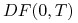 ,
, -
jest wypukła.
-
-
(b) Funkcja
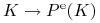
-
jest rosnąca,
-
spełnia warunek Lipschitza ze stałą
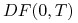 ,
,
-
jest wypukła.
-
Niech ![]() . Mamy udowodnić, że
wówczas
. Mamy udowodnić, że
wówczas
| (6.10) | |||
Rozpatrzmy przypadek opcji kupna. Przypuśćmy, że nierówność
(6.10a) nie zachodzi, czyli, że ![]() . W tej sytuacji przeprowadzamy następujące
transakcje:
. W tej sytuacji przeprowadzamy następujące
transakcje:
-
sprzedajemy opcję kupna z ceną wykonania
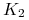 ,
, -
kupujemy opcję kupna z ceną wykonania
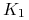 .
.
Różnicę ![]() lokujemy na
rachunku bankowym. Ponadto, w chwili wygaśnięcia opcji mamy
następujące możliwości:
lokujemy na
rachunku bankowym. Ponadto, w chwili wygaśnięcia opcji mamy
następujące możliwości:
-
(i)
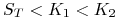 – obie opcje są bezwartościowe,
– obie opcje są bezwartościowe, -
(ii)
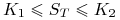 – opcja sprzedana jest bezwartościowa, a z kupionej
opcji realizujemy zysk
– opcja sprzedana jest bezwartościowa, a z kupionej
opcji realizujemy zysk 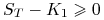 ,
, -
(iii)
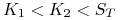 – na sprzedanej opcji mamy stratę
– na sprzedanej opcji mamy stratę 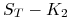 , na kupionej
zysk
, na kupionej
zysk 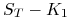 , czyli w sumie mamy zysk
, czyli w sumie mamy zysk 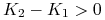 .
.
Tak więc z dodatnim prawdopodobieństwem ta strategia daje zysk. Zatem jest to strategia arbitrażowa, a to oznacza że musi zachodzić (6.10a).
Analogiczny dowód przeprowadzamy dla opcji sprzedaży.
Korzystając z parytetu opcji kupna/sprzedaży raz dla opcji z ceną
wykonania ![]() , a drugi raz dla opcji z ceną wykonania
, a drugi raz dla opcji z ceną wykonania ![]() ,
otrzymamy
,
otrzymamy
| (6.11) |
Z (6.11) oraz z monotoniczności funkcji ![]() i
i ![]() wynika iż funkcje
te spełniają warunek Lipschitza ze stałą równą
wynika iż funkcje
te spełniają warunek Lipschitza ze stałą równą ![]() .
.
Wypukłość funkcji ![]() oznacza że dla
każdych
oznacza że dla
każdych ![]() oraz każdego
oraz każdego ![]() zachodzi
zachodzi
| (6.12) |
Przypuśćmy, że (6.12) nie zachodzi. Wówczas, dla pewnych
![]() ,
, ![]() , oraz dla
, oraz dla ![]() mamy nierówność
mamy nierówność
| (6.13) |
Wtedy następująca strategia:
-
sprzedajemy opcję kupna z ceną wykonania
 ,
, -
kupujemy
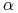 opcji kupna z ceną wykonania
opcji kupna z ceną wykonania 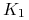 ,
, -
kupujemy
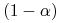 opcji kupna z ceną wykonania
opcji kupna z ceną wykonania 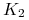 ,
,
jest strategią arbitrażową (Zadanie na Ćwiczenia).
Wypukłość funkcji ![]() wynika z wypukłości
funkcji
wynika z wypukłości
funkcji ![]() i parytetu opcji
kupna/sprzedaży.
i parytetu opcji
kupna/sprzedaży.
Uwaga 6.5
Monotoniczność funkcji ![]() i
i ![]() można
również uzasadnić racjonalnie w następujący sposób. Na przykład w
przypadku opcji kupna, wraz ze wzrostem ceny wykonania
można
również uzasadnić racjonalnie w następujący sposób. Na przykład w
przypadku opcji kupna, wraz ze wzrostem ceny wykonania ![]() maleją:
(a) prawdopodobieństwo tego, że w chwili wygaśnięcia opcji
maleją:
(a) prawdopodobieństwo tego, że w chwili wygaśnięcia opcji ![]() , oraz (b) wartość wypłaty opcji.
, oraz (b) wartość wypłaty opcji.
6.9. Zależność wartości opcji europejskiej od ceny instrumentu podstawowego
Twierdzenie 6.7
Rozpatrzmy opcje europejskie na ten sam instrument podstawowy o
ustalonym czasie trwania ![]() i ustalonej cenie wykonania
i ustalonej cenie wykonania ![]() . Niech
teraz
. Niech
teraz ![]() (
(![]() ) oznacza cenę opcji kupna
(sprzedaży) przy bieżącej cenie instrumentu podstawowego
) oznacza cenę opcji kupna
(sprzedaży) przy bieżącej cenie instrumentu podstawowego ![]() .
.
-
(a) Funkcja
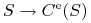
-
jest rosnąca,
-
spełnia warunek Lipschitza ze stała równą
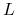 ,
, -
jest wypukła.
-
-
(b) Funkcja
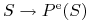
-
jest malejąca,
-
spełnia warunek Lipschitza ze stała równą
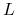 ,
, -
jest wypukła,
gdzie ![]() dla opcji na instrument podstawowy,
który generuje ciągły dochód ze stopą
dla opcji na instrument podstawowy,
który generuje ciągły dochód ze stopą ![]() , lub
, lub ![]() w pozostałych
przypadkach.
w pozostałych
przypadkach.
Dowód tego twierdzenia przebiega w sposób podobny do dowodu
przeprowadzonego w przypadku poprzedniego twierdzenia. Jednakże, aby
móc przeprowadzić analogiczne rozumowania arbitrażowe musimy
wprowadzić instrumenty podstawowe, które, poza tym że różnią się
bieżącymi cenami, są identyczne z instrumentem podstawowym. Na
przykład, w dowodzie monotoniczności zakładamy, że mamy dwa
instrumenty podstawowe, jeden o cenie bieżącej ![]() i drugi
identyczny ale o cenie bieżącej
i drugi
identyczny ale o cenie bieżącej ![]() .
.
Można pokazać, że własności opcji europejskich opisane w
Twierdzeniach 6.6 i 6.7 zachodzą również w
przypadku opcji amerykańskich, przy czym warunki Lipschitza
sformułowane w tych twierdzeniach zachodzą jedynie ze stałymi ![]() .
Jednakże, dowody tych twierdzeń dla opcji amerykańskich są bardziej
skomplikowane.
.
Jednakże, dowody tych twierdzeń dla opcji amerykańskich są bardziej
skomplikowane.
6.10. Wartość czasowa opcji
Wartość wewnętrzna opcji waniliowej w chwili ![]() , gdzie
, gdzie
![]() jest terminem wygaśnięcia opcji, to
jest terminem wygaśnięcia opcji, to
-
dla opcji kupna wielkość
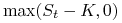 ,
, -
dla opcji sprzedaży wielkość
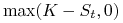 .
.
Wartość czasowa opcji waniliowej w chwili ![]() , gdzie
, gdzie ![]() jest terminem wygaśnięcia opcji, to różnica między wartością opcji w
chwili
jest terminem wygaśnięcia opcji, to różnica między wartością opcji w
chwili ![]() a jej wartością wewnętrzną, czyli
a jej wartością wewnętrzną, czyli
-
dla opcji kupna:
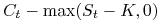 ,
, -
dla opcji sprzedaży:
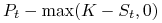 .
.
Terminologia
Opcja kupna jest w chwili ![]()
-
w cenie (ang. in the money, ITM), jeżeli
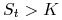 ,
, -
po cenie (ang. at the money, ATM), jeżeli
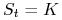 ,
, -
poza ceną (ang. out of the money, OTM), jeżeli
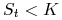 .
.
Opcja sprzedaży jest w chwili ![]()
-
w cenie (ang. in the money, ITM), jeżeli
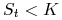 ,
, -
po cenie (ang. at the money, ATM), jeżeli
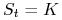 ,
, -
poza ceną (ang. out of the money, OTM), jeżeli
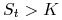 .
.
Wartość czasowa europejskiej opcji kupna na aktywo nie dające dochodu:
-
Dla opcji poza ceną, to znaczy gdy
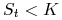 , wartość czasowa
jest równa wartości opcji.
, wartość czasowa
jest równa wartości opcji. -
Dla opcji w cenie, to znaczy gdy
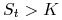 , wartość czasowa
jest większa niż
, wartość czasowa
jest większa niż 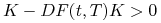 , bowiem jak wynika z Twierdzenia
6.4,
, bowiem jak wynika z Twierdzenia
6.4,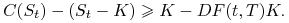
Wartość czasowa europejskiej opcji sprzedaży na aktywo nie dające dochodu:
-
Dla opcji poza ceną, to znaczy gdy
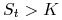 , wartość czasowa
jest równa wartości opcji.
, wartość czasowa
jest równa wartości opcji. -
Dla opcji w cenie, to znaczy gdy
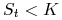 , wartość czasowa opcji
może być ujemna. Jeśli cena bieżąca
, wartość czasowa opcji
może być ujemna. Jeśli cena bieżąca 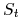 jest dostatecznie mała to,
jak wynika z Twierdzenia 6.4
jest dostatecznie mała to,
jak wynika z Twierdzenia 6.4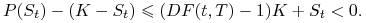
Twierdzenie 6.8
Wartość czasowa opcji w chwili jest największa dla opcji po cenie,
to znaczy gdy ![]() .
.
Rozpatrzmy przypadek opcji kupna. Na przedziale ![]() wartość
wewnętrzna opcji kupna jest zerowa i wartość czasowa opcji pokrywa
się z wartością opcji. Ponieważ wartość opcji kupna jest funkcją
rosnącą ceny instrumentu podstawowego to wartość czasowa opcji dla
wartość
wewnętrzna opcji kupna jest zerowa i wartość czasowa opcji pokrywa
się z wartością opcji. Ponieważ wartość opcji kupna jest funkcją
rosnącą ceny instrumentu podstawowego to wartość czasowa opcji dla
![]() będzie największa dla
będzie największa dla ![]() .
.
Teraz wystarczy udowodnić, że na przedziale ![]() wartość
czasowa opcji kupna jest funkcją malejącą ceny instrumentu
podstawowego. Niech
wartość
czasowa opcji kupna jest funkcją malejącą ceny instrumentu
podstawowego. Niech ![]() . Wówczas, na mocy
Twierdzenia 6.7
. Wówczas, na mocy
Twierdzenia 6.7
Stąd po przekształceniach otrzymujemy
co oznacza, że ![]() jest malejąca.
jest malejąca.
W przypadku opcji sprzedaży dowód jest analogiczny.
∎Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 6.1
Udowodnij równość (6.2) (parytet kupna/sprzedaży opcji, których instrument podstawowy daje ,,dyskretny” dochód). W tym celu:
-
(a) Przypuśćmy, że
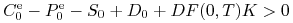 . Pokaż, że
strategia
. Pokaż, że
strategia-
kupno opcji sprzedaży,
-
kupno instrumentu podstawowego,
-
sprzedaż opcji kupna,
-
pożyczka kwoty
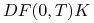 na czas trwania opcji po stopie
wolnej od ryzyka,
na czas trwania opcji po stopie
wolnej od ryzyka, -
pożyczka kwoty
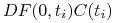 na okres
kończący się w
na okres
kończący się w 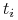 opcji po stopie wolnej od ryzyka (dla każdego
opcji po stopie wolnej od ryzyka (dla każdego
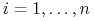 ),
),
zawiązana w
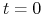 , jest strategią arbitrażową.
, jest strategią arbitrażową. -
-
(b) Przypuśćmy, że
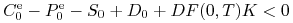 . Pokaż, że
strategia
. Pokaż, że
strategia-
sprzedaż opcji sprzedaży,
-
krótka sprzedaż instrumentu podstawowego,
-
kupno opcji kupna,
-
ulokowanie kwoty
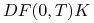 na czas trwania opcji po stopie wolnej od ryzyka,
na czas trwania opcji po stopie wolnej od ryzyka, -
ulokowanie kwoty
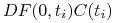 na okres
kończący się w
na okres
kończący się w 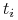 opcji po stopie wolnej od ryzyka (dla każdego
opcji po stopie wolnej od ryzyka (dla każdego
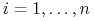 ),
),
zawiązana w
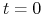 , jest strategią arbitrażową.
, jest strategią arbitrażową. -
Ćwiczenie 6.2
Udowodnij nierówności (6.8) w przypadku gdy instrument podstawowy nie przynosi dochodu w trakcie trwania opcji, oraz gdy struktura stóp procentowych wolnych od ryzyka jest płaska i nie zmienia się w czasie trwania opcji:
-
(a) Przypuśćmy, że
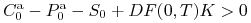 . Pokaż, że
strategia
. Pokaż, że
strategia-
kupno opcji sprzedaży,
-
kupno instrumentu podstawowego,
-
sprzedaż opcji kupna,
-
pożyczka kwoty
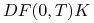 na czas trwania opcji po stopie
wolnej od ryzyka,
na czas trwania opcji po stopie
wolnej od ryzyka,
zawiązana w
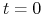 , jest strategią arbitrażową.
, jest strategią arbitrażową. -
-
(b) Przypuśćmy, że
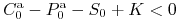 . Pokaż, że
strategia
. Pokaż, że
strategia-
sprzedaż opcji sprzedaży,
-
krótka sprzedaż instrumentu podstawowego,
-
kupno opcji kupna,
-
ulokowanie kwoty
 na czas trwania opcji po stopie
wolnej od ryzyka,
na czas trwania opcji po stopie
wolnej od ryzyka,
zawiązana w
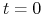 , jest strategią arbitrażową.
, jest strategią arbitrażową. -
Ćwiczenie 6.3
Dokończyć dowód wypukłości funkcji ![]() (patrz Twierdzenie 6.6).
(patrz Twierdzenie 6.6).
Ćwiczenie 6.4
Przeprowadź dowód Twierdzenia 6.8 w przypadku opcji sprzedaży.
Ćwiczenie 6.5 (Delty europejskich opcji waniliowych)
Załóżmy, że funkcje ![]() i
i ![]() są różniczkowalne. Pierwsze pochodne tych funkcji,
tzw. ,,delty” opcji
są różniczkowalne. Pierwsze pochodne tych funkcji,
tzw. ,,delty” opcji
są podstawowymi współczynnikami wrażliwości, które określają ,,ryzyko” opcji (portfeli opcji). Pokaż, że
-
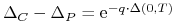 ,
, -
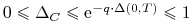 ,
, -
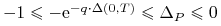 .
.
Ćwiczenie 6.6 (Gamma europejskich opcji waniliowych)
Załóżmy, że funkcje ![]() i
i ![]() są dwukrotnie różniczkowalne. Drugie pochodne tych
funkcji, tzw. ,,gammy” opcji
są dwukrotnie różniczkowalne. Drugie pochodne tych
funkcji, tzw. ,,gammy” opcji
są
współczynnikami wrażliwości drugiego rzędu, które określają
wrażliwość ,,delt” opcji (delt portfela opcji) na zmianę ceny
instrumentu podstawowego. Pokaż, że ![]()
Ćwiczenie 6.7 (Vega europejskich opcji waniliowych)
Wartość opcji zależy również od wielkości ![]() , która określa
poziom zmienności ceny instrumentu podstawowego. Załóżmy, że funkcje
, która określa
poziom zmienności ceny instrumentu podstawowego. Załóżmy, że funkcje
![]() i
i ![]() są różniczkowalne. Pochodne tych funkcji, tzw.
,,vegi” opcji
są różniczkowalne. Pochodne tych funkcji, tzw.
,,vegi” opcji
są
współczynnikami wrażliwości, które określają wrażliwość wartości
opcji (portfela opcji) na zmianę zmienności ceny instrumentu
podstawowego. Pokaż, że ![]() i uzasadnij
dlaczego
i uzasadnij
dlaczego ![]() .
.
Ćwiczenie 6.8 (Europejskie opcje binarne typu Cash-or-Nothing)
-
(a) Wyprowadź parytet opcji kupna/sprzedaży dla europejskich opcji binarnych typu Cash-or-Nothing.
-
(b) Call spread. Statyczna replikacja opcji binarnej kupna typu Cash-or-Nothing, która daje wypłatę jeśli cena instrumentu podstawowego jest ostro większa niż cena wykonania
 . Pokaż, że strategia
złożona opcji waniliowych o czasie trwania identycznym jak opcja
binarna typu Cash-or-Nothing, kupionej z ceną wykonania
. Pokaż, że strategia
złożona opcji waniliowych o czasie trwania identycznym jak opcja
binarna typu Cash-or-Nothing, kupionej z ceną wykonania  i
sprzedanej z ceną wykonania
i
sprzedanej z ceną wykonania 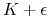 o wartościach nominalnych
o wartościach nominalnych
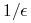 (sztuk instrumentu podstawowego) ma wypłatę która w
przybliżeniu pokrywa się z wypłatą opcji binarnej kupna dla
dostatecznie małej wartości
(sztuk instrumentu podstawowego) ma wypłatę która w
przybliżeniu pokrywa się z wypłatą opcji binarnej kupna dla
dostatecznie małej wartości 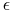 . Wówczas z prawa jednej ceny
wynika, że
. Wówczas z prawa jednej ceny
wynika, że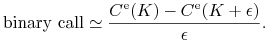
Uwaga: W praktyce
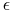 musi być co najmniej tak małe jak
minimalna wielkość zmiany ceny instrumentu podstawowego.
musi być co najmniej tak małe jak
minimalna wielkość zmiany ceny instrumentu podstawowego. -
(c) Jak wygląda replikacja opcji binarnej kupna typu Cash-or-Nothing, jeśli wypłata następuje gdy cena instrumentu podstawowego jest większa lub równa cenie wykonania
 ?
?
W praktyce rynkowej opcję typu Cash-or-Nothing wycenia się z call spreadu.
Ćwiczenie 6.9 (Europejskie opcje binarne typu Asset-or-Nothing)
-
(a) Wyprowadź parytet opcji kupna/sprzedaży dla europejskich opcji binarnych typu Asset-or-Nothing.
-
(b) Przestaw opcję waniliową jako portfel złożony z opcji binarnej typu Cash-or-Nothing oraz binarnej typu Asset-or-Nothing o odpowiednich nominałach.
-
(c) Korzystając z (b) sformułuj związek pomiędzy ceną opcji waniliowej a cenami opcji binarnych typu Cash-or-Nothing oraz typu Asset-or-Nothing.
W praktyce rynkowej opcję Asset-or-Nothing wycenia się za pomocą związku opisanego w (c) powyżej, w którym opcja Cash-or-Nothing jest wyceniana z call spreadu (patrz Zadanie 6.8).
Ćwiczenie 6.10 (Strategia motyla (Butterfly strategy))
Strategia motyla to portfel europejskich opcji waniliowych o następującym składzie:
-
dwóch kupionych opcji o cenach wykonania
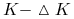 oraz
oraz 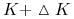 odpowiednio,
odpowiednio, -
dwóch sprzedanych opcji o cenie wykonania
 .
.
Wykreśl profil wypłaty tej strategii. W jaki sposób zbudować tę strategię korzystając z opcji sprzedaży?
Uwaga: Niech ![]() oraz
oraz ![]() gdzie
gdzie ![]() są ustalonymi cenami wykonania.
Strategia motyla jest szczególnym przypadkiem strategii polegającej
na kupnie
są ustalonymi cenami wykonania.
Strategia motyla jest szczególnym przypadkiem strategii polegającej
na kupnie ![]() sztuk opcji z ceną wykonania
sztuk opcji z ceną wykonania ![]() , kupnie
, kupnie
![]() sztuk opcji z ceną wykonania
sztuk opcji z ceną wykonania ![]() , oraz sprzedaży jednej
opcji z ceną wykonania
, oraz sprzedaży jednej
opcji z ceną wykonania ![]() , wszystkie o tym samym terminie
wykonania. Strategię tego typu można wykorzystać w dowodzie
wypukłości ceny opcji względem ceny wykonania.
, wszystkie o tym samym terminie
wykonania. Strategię tego typu można wykorzystać w dowodzie
wypukłości ceny opcji względem ceny wykonania.
Ćwiczenie 6.11 (Risk reversal strategy)
Strategia risk reversal to portfel europejskich opcji waniliowych o następującym składzie:
-
sprzedanej (kupionej) opcji sprzedaży z ceną wykonania
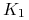 ,
, -
kupionej (sprzedanej) opcji kupna z ceną wykonania
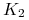 ,
,
gdzie ![]() . Na rynku OTC opcji walutowych, to jest opcji,
których instrumentem podstawowym jest kurs wymiany walut, kwotuje
się strategie risk reversal, w których obie opcje mają taką
samą deltę (co do wartości bezwzględnej), standardowo 0.25. Taką
strategię nazywa się wtedy 25 delta risk reversal strategy.
. Na rynku OTC opcji walutowych, to jest opcji,
których instrumentem podstawowym jest kurs wymiany walut, kwotuje
się strategie risk reversal, w których obie opcje mają taką
samą deltę (co do wartości bezwzględnej), standardowo 0.25. Taką
strategię nazywa się wtedy 25 delta risk reversal strategy.
Wykreśl profil wypłaty tej strategii.
Ćwiczenie 6.12 (Europejskie opcje ,,zapłać później” (Paylater options))
Wartość europejskiej opcji kupna ,,zapłać później” z ceną wykonania
![]() w chwili wygaśnięcia
w chwili wygaśnięcia ![]() wynosi
wynosi
-
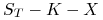 , jeśli
, jeśli 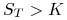 ,
, -
0, jeśli
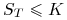 ,
,
gdzie ![]() jest premią opcji płaconą w chwili
jest premią opcji płaconą w chwili ![]() , ustalaną zwykle
tak, by w chwili zawarcia opcji jej wartość wynosiła zero.
, ustalaną zwykle
tak, by w chwili zawarcia opcji jej wartość wynosiła zero.
Analogicznie, wartość europejskiej opcji sprzedaży zapłać później z
ceną wykonania ![]() w chwili wygaśnięcia
w chwili wygaśnięcia ![]() wynosi
wynosi
-
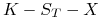 , jeśli
, jeśli 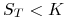 ,
, -
0, jeśli
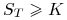 .
.
Wykreśl profil wypłat tych opcji. Przedstaw te opcje jako portfele złożone z opcji waniliowej i opcji binarnej.
Ćwiczenie 6.13 (Opcja wyboru (Chooser option))
Europejska opcja wyboru (chooser option) zapadalna w chwili
![]() to opcja waniliowa, w której dodatkowo posiadacz opcji w chwili
to opcja waniliowa, w której dodatkowo posiadacz opcji w chwili
![]() określa, czy posiadana przez niego opcja jest opcją kupna
czy opcją sprzedaży. Tak więc w chwili
określa, czy posiadana przez niego opcja jest opcją kupna
czy opcją sprzedaży. Tak więc w chwili ![]() ta opcja ma wartość
ta opcja ma wartość
gdzie ![]() ,
, ![]() są
wartościami opcji kupna i sprzedaży, odpowiednio. Załóżmy, że cena
wykonania obu opcji w jest taka sama i wynosi
są
wartościami opcji kupna i sprzedaży, odpowiednio. Załóżmy, że cena
wykonania obu opcji w jest taka sama i wynosi ![]() . Załóżmy, dla
uproszczenia, że instrument podstawowy opcji daje dochód płacony w
sposób ciągły ze stałą stopą
. Załóżmy, dla
uproszczenia, że instrument podstawowy opcji daje dochód płacony w
sposób ciągły ze stałą stopą ![]() (np. indeks giełdowy).
(np. indeks giełdowy).
-
(a) Pokaż, że
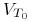 można przedstawić jako sumę wartości opcji kupna zapadalnej
w chwili
można przedstawić jako sumę wartości opcji kupna zapadalnej
w chwili  o cenie wykonania
o cenie wykonania  oraz wypłaty z opcji sprzedaży
zapadalnej w
oraz wypłaty z opcji sprzedaży
zapadalnej w 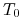 z odpowiednio dobraną ceną wykonania
z odpowiednio dobraną ceną wykonania 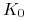 . Ile
wynosi
. Ile
wynosi 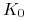 ?
? -
(b) Przedstaw opcję wyboru w postaci portfela odpowiednio dobranych waniliowej opcji kupna oraz waniliowej opcji sprzedaży. Korzystając z tego przedstawienia wyprowadź formuły na wycenę opcji wyboru w zależności od wartości odpowiednio dobranych opcji waniliowych.
Ćwiczenie 6.14
Dane są następujące kwotowania:
-
cena 3M opcji ATM (at-the-money) kupna 1 miliona USD za PLN (to jest opcji call na kurs wymiany USD/PLN o nominale 1 milion USD) wynosi:
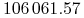 PLN,
PLN, -
bieżący kurs USD/PLN wynosi: 4.0000 (PLN za 1 USD),
-
3M punkty swapowe USD/PLN wynoszą: 0.0503,
-
3M stopa (kapitalizowana w sposób ciągły) dla PLN wynosi: 7.00%.
Przy założeniu, że na rynku nie ma możliwości do arbitrażu,
-
(a) oblicz cenę 3M opcji ATM (at-the-money) kupna
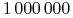 PLN za USD,
PLN za USD, -
(b) 3M depozytową stopę (wolną od ryzyka) dla USD.
Przypomnienie: Mówimy, że opcja jest ATM (at-the-money) jeśli bieżąca cena instrumentu podstawowego opcji jest równa cenie wykonania opcji.
Ćwiczenie 6.15
Wyprowadź parytet opcji kupna/sprzedaży dla europejskich opcji azjatyckich na dyskretną średnią arytmetyczną
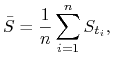 |
gdzie
![]() są ustalonymi chwilami czasu, w których
obserwowana jest wartość instrumentu podstawowego, a
są ustalonymi chwilami czasu, w których
obserwowana jest wartość instrumentu podstawowego, a ![]() jest
terminem zapadalności opcji. Załóż, że struktura stóp procentowych
jest płaska i stała w czasie trwania opcji. Parytet wyznacz dla
chwili czasu
jest
terminem zapadalności opcji. Załóż, że struktura stóp procentowych
jest płaska i stała w czasie trwania opcji. Parytet wyznacz dla
chwili czasu ![]() , to znaczy w trakcie trwania opcji,
po ustaleniu
, to znaczy w trakcie trwania opcji,
po ustaleniu ![]() pierwszych wartości instrumentu podstawowego.
pierwszych wartości instrumentu podstawowego.
Oblicz wartość kontraktu forward na średnią arytmetyczną ![]() z
ceną wykonania
z
ceną wykonania ![]() , który zapada w
, który zapada w ![]() . W tym celu, pokaż, że
wyceniając ten kontrakt, wartość każdego nieustalonego składnika
. W tym celu, pokaż, że
wyceniając ten kontrakt, wartość każdego nieustalonego składnika
![]() , gdzie
, gdzie ![]() , sumy określającej średnią
, sumy określającej średnią ![]() , można
zastąpić ceną forward
, można
zastąpić ceną forward ![]() wyznaczoną w chwili
wyznaczoną w chwili ![]() kontraktu
zapadalnego w
kontraktu
zapadalnego w ![]() .
.
Ćwiczenie 6.16
Bank Miejski oferuje klientom lokatę w PLN, która po upływie terminu
lokaty ![]() wypłaci kwotę
wypłaci kwotę
gdzie
-
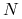 jest nominałem lokaty w PLN,
jest nominałem lokaty w PLN, -
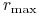 – maksymalną stopą oprocentowania lokaty,
– maksymalną stopą oprocentowania lokaty, -
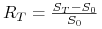 jest stopą zwrotu z indeksu WIG20 w okresie
lokaty,
jest stopą zwrotu z indeksu WIG20 w okresie
lokaty, -
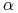 jest tak zwanym współczynnikiem partycypacji.
jest tak zwanym współczynnikiem partycypacji.
Jakie opcje waniliowe na WIG20 są wbudowane w tą lokatę?
Ćwiczenie 6.17 (Europejska opcja z barierą europejską)
Niech ![]() dla opcji kupna oraz
dla opcji kupna oraz ![]() dla opcji
sprzedaży, oraz niech
dla opcji
sprzedaży, oraz niech ![]() . Wypłata europejskiej
opcji kupna/sprzedaży z barierą europejską
. Wypłata europejskiej
opcji kupna/sprzedaży z barierą europejską ![]() i ceną wykonania
i ceną wykonania ![]() wynosi
wynosi
Wykreśl profil wypłat tych opcji. Przedstaw te opcje jako portfele złożone z opcji waniliowych i opcji binarnej Cash-or-Nothing o odpowiednich nominałach.
Ćwiczenie 6.18 (Lokata dwuwalutowa)
Inwestor lokuje w banku kwotę ![]() w walucie
w walucie ![]() na
okres czasu
na
okres czasu ![]() . Niech
. Niech ![]() oznacza kurs wymiany
oznacza kurs wymiany
![]() . W chwili
. W chwili ![]() zakończenia lokaty
inwestor otrzymuje
zakończenia lokaty
inwestor otrzymuje
-
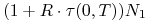 w walucie
w walucie 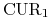 , jeśli
, jeśli 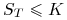 ,
, -
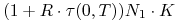 w walucie
w walucie  , jeśli
, jeśli 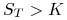 ,
,
gdzie ![]() jest ustalonym kursem wymiany (tzw. kurs konwersji), zaś
jest ustalonym kursem wymiany (tzw. kurs konwersji), zaś
![]() jest ułamkiem roku odpowiadającym bazie stopy
jest ułamkiem roku odpowiadającym bazie stopy ![]() .
.
Jaka opcja jest wbudowana w ten instrument? Załóżmy, że ![]() jest
stopą procentową dla standardowej lokaty złożonej na okres czasu
jest
stopą procentową dla standardowej lokaty złożonej na okres czasu
![]() . Jaka jest największa wartość stopy
. Jaka jest największa wartość stopy ![]() w zależności od cen
instrumentów wbudowanych w tą lokatę dwuwalutową, którą bank może
zaoferować inwestorowi nie tracąc na takim instrumencie?
w zależności od cen
instrumentów wbudowanych w tą lokatę dwuwalutową, którą bank może
zaoferować inwestorowi nie tracąc na takim instrumencie?
Ćwiczenie 6.19 (Jednorodność ceny opcji jako funkcji ceny bieżącej i ceny wykonania)
Uzasadnij dlaczego cena ![]() opcji waniliowej jest jednorodną funkcją
ceny bieżącej instrumentu podstawowego i ceny wykonania, to znaczy
opcji waniliowej jest jednorodną funkcją
ceny bieżącej instrumentu podstawowego i ceny wykonania, to znaczy
| (6.14) |
Zauważ, że dla ![]() zachodzi tożsamość
zachodzi tożsamość
gdzie ![]() dla
opcji kupna i
dla
opcji kupna i ![]() dla opcji sprzedaży.
dla opcji sprzedaży.
Korzystając z (6.14) pokaż, że jeśli ![]() jest funkcją
różniczkowalną względem
jest funkcją
różniczkowalną względem ![]() i
i ![]() , to
, to
Uwaga: Pochodna ceny opcji ![]() względem ceny wykonania
względem ceny wykonania ![]() jest
określana jako tak zwana delta dualna.
jest
określana jako tak zwana delta dualna.




