Zagadnienia
7. Model dwumianowy – jednookresowy
7.1. Model dwumianowy
Model dwumianowy jest prostym modelem za pomocą którego
-
opiszemy proces stochastyczny ceny aktywa,
-
skonstruujemy portfele replikujące instrumenty pochodne,
-
sformułujemy i uzasadnimy metodę wyceny instrumentów pochodnych.
Model opiszemy w dwóch etapach:
-
zaczniemy od modelu jednookresowego (Wykład 7),
który następnie rozszerzymy na
-
model wielookresowy (Wykład 8).
W modelu jednookresowym rozpatrujemy tylko dwa punkty w czasie
-
dziś –
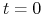 w którym znamy stan rynku,
w którym znamy stan rynku, -
jutro –
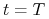 w którym stan rynku z dzisiejszej perspektywy
nie jest znany – ceny aktywów w
w którym stan rynku z dzisiejszej perspektywy
nie jest znany – ceny aktywów w  są zmiennymi losowymi.
są zmiennymi losowymi.
Na rynku mamy dwa aktywa
-
obligację zerokuponową (rachunek bankowy na którym lokaty/depozyty są oprocentowane według stopy zerokuponowej)
 proces (zmienna) deterministyczna,
proces (zmienna) deterministyczna, -
aktywo obarczone ryzykiem (np. akcja), które nie przynosi dochodu w okresie
![[0,T]](wyklady/ifi/mi/mi591.png)
 proces stochastyczny.
proces stochastyczny.
![]() Proces wartości obligacji zerokuponowej
(rachunku bankowego) –
Proces wartości obligacji zerokuponowej
(rachunku bankowego) – ![]()
-
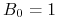 ,
, -
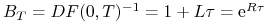 , gdzie
, gdzie 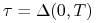 .
.
![]() Proces ceny aktywa –
Proces ceny aktywa – ![]()
-
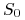 dane, znana wartość,
dane, znana wartość, -
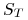 jest zmienną losową o następującym rozkładzie
jest zmienną losową o następującym rozkładzie![S_{T}=\left\{\begin{array}[]{ll}S_{0}\, U,&\hbox{z prawdopodobieństwem $p$ (stan ,,up''),}\\
S_{0}\, D,&\hbox{z prawdopodobieństwem $1-p$ (stan ,,down'').}\end{array}\right.](wyklady/ifi/mi/mi891.png)
gdzie
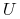 i
i 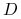 są dane, przy czym
są dane, przy czym 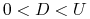 . Później pokażemy jak te
wielkości powiązać z innymi parametrami aktywa, w szczególności ze
zmiennością aktywa. Okaże się również, że wartość prawdopodobieństwa
. Później pokażemy jak te
wielkości powiązać z innymi parametrami aktywa, w szczególności ze
zmiennością aktywa. Okaże się również, że wartość prawdopodobieństwa
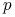 nie będzie istotna przy wycenie instrumentów pochodnych
wystawionych na
nie będzie istotna przy wycenie instrumentów pochodnych
wystawionych na  (istotna będzie miara prawdopodobieństwa w tzw.
świecie wolnym od ryzyka).
(istotna będzie miara prawdopodobieństwa w tzw.
świecie wolnym od ryzyka).
Zmienną ![]() możemy zapisać w postaci
możemy zapisać w postaci
gdzie ![]() jest następującą zmienną losową
jest następującą zmienną losową
![]() Europejski instrument pochodny
Europejski instrument pochodny ![]() , wystawiony
na ryzykowne aktywo
, wystawiony
na ryzykowne aktywo ![]() , to instrument finansowy, którego wartość
wypłaty w chwili zapadalności
, to instrument finansowy, którego wartość
wypłaty w chwili zapadalności ![]() jest zmienną losową postaci
jest zmienną losową postaci
gdzie ![]() jest pewną funkcją.
jest pewną funkcją.
Na przykład, dla europejskiej opcji kupna akcji ![]() z ceną wykonania
z ceną wykonania
![]() , która wygasa w
, która wygasa w ![]() , mamy
, mamy
przy założeniu, że ![]() .
.
Jedna z metod wyceny instrumentów pochodnych będzie polegała na konstrukcji portfela replikującego dany instrument pochodny, to znaczy portfela którego wartość w terminie zapadalności instrumentu pochodnego będzie taka sama jak wypłata, którą da instrument pochodny. Sformalizujemy pojęcie portfela w następujący sposób.
![]() Portfel na rynku, na którym dostępne
są obligacja (rachunek bankowy) i jedno ryzykowne aktywo, to para
Portfel na rynku, na którym dostępne
są obligacja (rachunek bankowy) i jedno ryzykowne aktywo, to para
![]() , gdzie
, gdzie ![]() oznacza kwotę pieniędzy zainwestowaną w
obligacje (złożoną na rachunku bankowym), a
oznacza kwotę pieniędzy zainwestowaną w
obligacje (złożoną na rachunku bankowym), a ![]() oznacza ilość
ryzykownego aktywa w portfelu.
oznacza ilość
ryzykownego aktywa w portfelu.
Założenia
-
krótka sprzedaż jest dozwolona

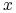 i
i 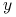 mogą
być ujemne,
mogą
być ujemne, -
jest nieskończona podzielność aktywów

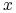 i
i 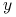 nie muszą być całkowite,
nie muszą być całkowite, -
nie ma widełek kupna-sprzedaży,
-
jest pełna płynność obu aktywów.
![]() Wartość portfela
Wartość portfela ![]() :
:
-
w chwili
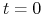 utworzenia portfela wynosi
utworzenia portfela wynosi
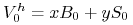 i jest znaną wartością, jeśli
i jest znaną wartością, jeśli 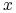 i
i 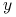 są dane,
są dane, -
w przyszłej chwili
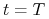 jest zmienną losową
jest zmienną losową
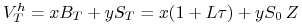 .
.
Sprawiedliwa cena instrumentu pochodnego będzie ceną, przy której arbitraż nie będzie możliwy. Sprecyzujemy pojęcie portfela arbitrażowego.
![]() Portfel arbitrażowy to portfel
Portfel arbitrażowy to portfel ![]() ,
który spełnia następujące warunki:
,
który spełnia następujące warunki:
-
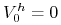
 nie ponosimy żadnych kosztów
początkowych by utworzyć portfel,
nie ponosimy żadnych kosztów
początkowych by utworzyć portfel, -
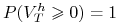 ,
, -
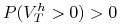 .
.
W jakich warunkach nasz model rynku nie dopuszcza arbitrażu? Odpowiedź na to pytanie zawarta jest w następującym lemacie:
Lemat 7.1
Model jednookresowy rynku z parametrami ![]() nie dopuszcza
arbitrażu wtedy i tylko wtedy gdy
nie dopuszcza
arbitrażu wtedy i tylko wtedy gdy
| (7.1) |
gdzie ![]() .
.
(![]() ) Przypuśćmy, że (7.1) nie zachodzi. Wówczas,
) Przypuśćmy, że (7.1) nie zachodzi. Wówczas,
![]() lub
lub ![]() . Rozpatrzmy przypadek
. Rozpatrzmy przypadek
![]() . Wtedy mamy także
. Wtedy mamy także ![]() . Skąd wynika, że
zawsze (niezależnie od stanu rynku) inwestycja w obligację (lokatę
na rachunku bankowym) nie będzie mniej opłacalna niż inwestycja w
aktywo. Tak więc, tworzymy portfel
. Skąd wynika, że
zawsze (niezależnie od stanu rynku) inwestycja w obligację (lokatę
na rachunku bankowym) nie będzie mniej opłacalna niż inwestycja w
aktywo. Tak więc, tworzymy portfel ![]() , to znaczy krótko
sprzedajemy aktywo i pieniądze uzyskane ze sprzedaży aktywa
inwestujemy w obligację. Jasne, że
, to znaczy krótko
sprzedajemy aktywo i pieniądze uzyskane ze sprzedaży aktywa
inwestujemy w obligację. Jasne, że ![]() oraz że
oraz że
w każdym stanie rynku. Ponadto, w stanie ,,down”
![]() . Tak więc
. Tak więc ![]() jest portfelem arbitrażowym. Podobne rozumowanie możemy
przeprowadzić w przypadku gdy
jest portfelem arbitrażowym. Podobne rozumowanie możemy
przeprowadzić w przypadku gdy ![]() .
.
(![]() ) Niech
) Niech ![]() będzie dowolnym portfelem takim, że
będzie dowolnym portfelem takim, że
![]() . Wówczas
. Wówczas ![]() , a jego wartość w
, a jego wartość w ![]() wynosi
wynosi
Przypuśćmy, że arbitraż jest możliwy. W przypadku ![]()
![]() jest
portfelem arbitrażowym wtedy i tylko wtedy, gdy
jest
portfelem arbitrażowym wtedy i tylko wtedy, gdy ![]() oraz
oraz
![]() , i przynajmniej jedna z tych nierówności jest ostra.
Wtedy mamy sprzeczność z (7.1). W przypadku
, i przynajmniej jedna z tych nierówności jest ostra.
Wtedy mamy sprzeczność z (7.1). W przypadku ![]() do
sprzeczności dochodzimy w podobny sposób.
do
sprzeczności dochodzimy w podobny sposób.
Warunek z Lematu 7.1 możemy przeformułować w następujący sposób:
(![]() ) Oczywiste.
) Oczywiste.
(![]() ) Definiujemy (rozwiązujemy równanie (7.2)
przy warunku
) Definiujemy (rozwiązujemy równanie (7.2)
przy warunku ![]() ):
):
| (7.3) |
Łatwo sprawdzić, że są to szukane wartości.
∎7.2. Świat wolny od ryzyka
![]() zadają nowe prawdopodobieństwo
zadają nowe prawdopodobieństwo ![]() na przestrzeni stanów
rynku w
na przestrzeni stanów
rynku w ![]() . Niech
. Niech ![]() oznacza wartość oczekiwaną względem miary
prawdopodobieństwa
oznacza wartość oczekiwaną względem miary
prawdopodobieństwa ![]() . Wówczas, jak łatwo można pokazać
. Wówczas, jak łatwo można pokazać
| (7.4) |
czyli w świecie z miarą ![]() oczekiwany zwrot z ryzykownego
aktywa jest równy zwrotowi z aktywa wolnego od ryzyka. Z tego powodu
miarę
oczekiwany zwrot z ryzykownego
aktywa jest równy zwrotowi z aktywa wolnego od ryzyka. Z tego powodu
miarę ![]() określa się terminem miara wolna od ryzyka, a
przestrzeń stanów rynku z tą miarą nazywamy światem wolnym od
ryzyka.
określa się terminem miara wolna od ryzyka, a
przestrzeń stanów rynku z tą miarą nazywamy światem wolnym od
ryzyka.
Wzór (7.4) możemy przepisać w następującej postaci
| (7.5) |
i wtedy oznacza on, że bieżąca cena ryzykownego aktywa jest równa
zdyskontowanej po stopie wolnej od ryzyka wartości oczekiwanej
(względem miary ![]() ) przyszłej ceny
) przyszłej ceny ![]() . Niech
. Niech
będzie procesem zdyskontowanej ceny aktywa. Wówczas (7.5) możemy przeformułować w następujący sposób:
co matematycznie możemy wyrazić mówiąc iż zdyskontowany proces cen
jest martyngałem. Dlatego też o mierze ![]() mówimy że jest to wolna
od ryzyka miara martyngałowa.
mówimy że jest to wolna
od ryzyka miara martyngałowa.
7.3. Wycena instrumentów pochodnych
Niech
oznacza cenę instrumentu pochodnego ![]() w chwili
czasu
w chwili
czasu ![]() . Jasne, że w chwili zapadalności
. Jasne, że w chwili zapadalności ![]() instrumentu
instrumentu ![]() jego cena pokrywa się z wartością wypłaty, czyli że
jego cena pokrywa się z wartością wypłaty, czyli że
![]() .
.
Jak natomiast wyznaczyć sprawiedliwą cenę ![]() w chwili bieżącej
w chwili bieżącej
![]() ? Zrobimy to tak:
? Zrobimy to tak:
-
zreplikujemy instrument pochodny
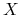 portfelem
portfelem 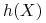 złożonym
z obligacji zerokuponowej (lokaty/depozytu) i aktywa
złożonym
z obligacji zerokuponowej (lokaty/depozytu) i aktywa  ,
, -
za cenę instrumentu pochodnego
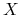 przyjmiemy wartość portfela
replikującego, to znaczy przyjmiemy, że
przyjmiemy wartość portfela
replikującego, to znaczy przyjmiemy, że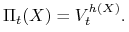
W szczególności, będziemy mieli (zasada wyceny instrumentów pochodnych)
| (7.6) |
bowiem każda inna cena prowadziłaby do arbitrażu.
Będzie to dobry model wyceny, jeżeli będziemy wiedzieli, że każdy instrument pochodny możemy tak wycenić, czyli gdy każdy instrument pochodny będziemy w stanie zreplikować w naszym modelu rynku. W tym kontekście wprowadzimy następujące definicje:
-
Instrument pochodny
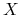 jest osiągalny, jeżeli istnieje
portfel
jest osiągalny, jeżeli istnieje
portfel 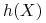 taki że
taki że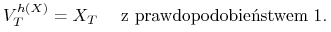
Portfel
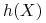 nazywamy portfelem
replikującym, a
nazywamy portfelem
replikującym, a 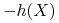 portfelem
zabezpieczającym.
portfelem
zabezpieczającym. -
Jeżeli każdy instrument pochodny
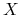 jest osiągalny na
danym rynku, to mówimy, że rynek jest zupełny.
jest osiągalny na
danym rynku, to mówimy, że rynek jest zupełny.
W naszym prostym przypadku mamy następujące
Twierdzenie 7.1
Jeżeli model jednookresowy jest wolny od arbitrażu, to ten model rynku jest zupełny, to znaczy, każdy instrument pochodny na tym rynku jest osiągalny.
Niech ![]() będzie dowolnym instrumentem pochodnym zapadalnym
w
będzie dowolnym instrumentem pochodnym zapadalnym
w ![]() , którego instrumentem podstawowym jest aktywo
, którego instrumentem podstawowym jest aktywo ![]() . Pokażemy,
że istnieje portfel
. Pokażemy,
że istnieje portfel ![]() taki, że
taki, że
Niech ![]() . Wówczas z powyższego warunku wynika następujący
układ równań na niewiadome
. Wówczas z powyższego warunku wynika następujący
układ równań na niewiadome ![]() ,
, ![]() :
:
Ponieważ ![]() , układ ten ma jednoznaczne rozwiązanie
, układ ten ma jednoznaczne rozwiązanie
| (7.7) |
A więc istnieje portfel ![]() replikujący
replikujący ![]() .
.
Niech ![]() będzie instrumentem pochodnym, a
będzie instrumentem pochodnym, a ![]() jego
portfelem replikującym skład którego dany jest wzorami
(7.7). Wówczas zgodnie z zasadą wyceny instrumentów
pochodnych (7.6), cena
jego
portfelem replikującym skład którego dany jest wzorami
(7.7). Wówczas zgodnie z zasadą wyceny instrumentów
pochodnych (7.6), cena ![]() w
w ![]() dana jest wzorem
dana jest wzorem
Dotychczasowe rezultaty zbierzemy w następującym twierdzeniu.
Twierdzenie 7.2
Jeżeli model jednookresowy nie dopuszcza arbitrażu, to sprawiedliwa
cena instrumentu pochodnego ![]() dana jest wzorem
dana jest wzorem
gdzie ![]() jest wolną od
ryzyka miarą martyngałową wyznaczoną przez warunek
jest wolną od
ryzyka miarą martyngałową wyznaczoną przez warunek
Instrument pochodny ![]() można
zreplikować portfelem
można
zreplikować portfelem ![]() , gdzie
, gdzie
7.4. Alternatywne wyprowadzenie wzorów na wycenę instrumentu pochodnego
Rozpatrzmy instrument pochodny ![]() wygasający w chwili
wygasający w chwili ![]() ,
którego instrumentem podstawowym jest aktywo
,
którego instrumentem podstawowym jest aktywo ![]() . Tworzymy portfel
który składa się z
. Tworzymy portfel
który składa się z
-
 jednostek aktywa,
jednostek aktywa, -
wystawionego (sprzedanego) instrumentu pochodnego
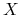 .
.
Wartość tego portfela w chwili ![]() wynosi
wynosi
Chcemy by ten portfel był pozbawiony ryzyka, to znaczy, by niezależnie od stanu rynku jego wartość była taka sama, czyli by zachodziła równość
Rozwiązując to równanie ze względu na zmienną ![]() otrzymujemy
otrzymujemy
| (7.8) |
Zauważmy, że ![]() , gdzie
, gdzie ![]() określa ilość aktywa w portfelu
replikującym
określa ilość aktywa w portfelu
replikującym ![]() (patrz (7.7)). Gdy
(patrz (7.7)). Gdy ![]() jest wyznaczone
wzorem (7.8), nasz portfel jest pozbawiony ryzyka. Dochód,
który da ten portfel, musi być taki sam jak dochód z inwestycji w
obligację zerokuponową (lokatę/depozyt) ze stopą
jest wyznaczone
wzorem (7.8), nasz portfel jest pozbawiony ryzyka. Dochód,
który da ten portfel, musi być taki sam jak dochód z inwestycji w
obligację zerokuponową (lokatę/depozyt) ze stopą ![]() . Ponieważ koszt
utworzenia tego portfela w
. Ponieważ koszt
utworzenia tego portfela w ![]() wynosi
wynosi
w chwili
![]() musi zachodzić
musi zachodzić
Z tego równania
możemy wyliczyć wartość ![]() . Otrzymamy
. Otrzymamy
| (7.9) |
a po podstawieniu do (7.9) formuły (7.8) na ![]() i
wykonaniu odpowiednich przekształceń, wzór (7.9)
przedstawimy znów w postaci
i
wykonaniu odpowiednich przekształceń, wzór (7.9)
przedstawimy znów w postaci
Uwaga 7.1
Często do wyrażenia stopy dochodu z inwestycji wolnej od
ryzyka, zamiast stopy prostej ![]() , używa się stopy kapitalizowanej w
sposób ciągły (stopy logarytmicznego zwrotu)
, używa się stopy kapitalizowanej w
sposób ciągły (stopy logarytmicznego zwrotu) ![]() . Podobnie, zamiast
czynnika dyskontowego postaci
. Podobnie, zamiast
czynnika dyskontowego postaci ![]() , używa się ceny
obligacji zerokuponowej zapadalnej w
, używa się ceny
obligacji zerokuponowej zapadalnej w ![]() . Wtedy w odpowiednich
wyrażeniach należy zastąpić
. Wtedy w odpowiednich
wyrażeniach należy zastąpić ![]() przez
przez ![]() lub
lub
![]() .
.
Przykład 7.1
Niech cena akcji w chwili ![]() wynosi
wynosi ![]() , a stopa wolna od
ryzyka kapitalizowana w sposób ciągły
, a stopa wolna od
ryzyka kapitalizowana w sposób ciągły ![]() . Rozpatrzmy
trzymiesięczną opcję kupna z ceną wykonania
. Rozpatrzmy
trzymiesięczną opcję kupna z ceną wykonania ![]() . Dla uproszczenia
obliczeń przyjmijmy, że
. Dla uproszczenia
obliczeń przyjmijmy, że ![]() . Załóżmy, że cena akcji albo
wzrośnie o
. Załóżmy, że cena akcji albo
wzrośnie o ![]() albo zmaleje o
albo zmaleje o ![]() , czyli że
, czyli że ![]() oraz
oraz
![]() . Tak więc w
. Tak więc w ![]() , cena akcji wynosi
, cena akcji wynosi
a wartość wypłaty z opcji
Wyznaczamy miarę wolną od ryzyka, czyli prawdopodobieństwo
Uwaga: wartość ![]() możemy również obliczyć z równania
możemy również obliczyć z równania
Zgodnie z zasadą
wyceny instrumentów pochodnych cena opcji w ![]() wynosi
wynosi
Tą samą wartość
otrzymamy obliczając wartość portfela replikującego w ![]() .
Mianowicie, skład portfela replikującego jest następujący
.
Mianowicie, skład portfela replikującego jest następujący
a jego wartość w ![]() wynosi
wynosi
Wróćmy do świata realnego. Przypuśćmy, że oczekiwana logarytmiczna
(kapitalizowana w sposób ciągły) stopa zwrotu z akcji wynosi 16%.
Prawdopodobieństwo ![]() wzrostu ceny akcji w świecie realnym
obliczamy z równania
wzrostu ceny akcji w świecie realnym
obliczamy z równania
skąd ![]() . W świecie realnym oczekiwana
wypłata z opcji wynosi
. W świecie realnym oczekiwana
wypłata z opcji wynosi
Jaką
stopą ![]() należy zdyskontować tą oczekiwaną wypłatę opcji, by
otrzymać cenę opcji? Obliczamy ją z warunku
należy zdyskontować tą oczekiwaną wypłatę opcji, by
otrzymać cenę opcji? Obliczamy ją z warunku
skąd ![]() , a więc dużo więcej
niż 16%, i słusznie bowiem opcja jest instrumentem bardziej
ryzykownym niż akcja.
, a więc dużo więcej
niż 16%, i słusznie bowiem opcja jest instrumentem bardziej
ryzykownym niż akcja.
7.5. Wyznaczanie wartości współczynników 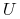 i
i 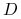
Chcemy powiązać wartości współczynników ![]() i
i ![]() z podstawowymi
parametrami procesu cen aktywa
z podstawowymi
parametrami procesu cen aktywa ![]() . Tymi parametrami będą
. Tymi parametrami będą
-
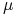 – logarytmiczna stopa oczekiwanego zwrotu z aktywa, czyli
liczba taka, że
– logarytmiczna stopa oczekiwanego zwrotu z aktywa, czyli
liczba taka, że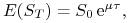
-
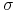 – odchylenie standardowe logarytmicznej stopy zwrotu z aktywa
– tzw. zmienność aktywa – liczba taka, że
– odchylenie standardowe logarytmicznej stopy zwrotu z aktywa
– tzw. zmienność aktywa – liczba taka, że
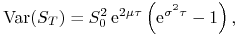
(7.10)
przy czym obie wielkości są podane w skali roku (zannualizowane).
Oczywiście, w przypadku tworzenia drzewa dwumianowego w celu wyceny
instrumentu pochodnego przyjmujemy ![]() , gdzie
, gdzie ![]() jest stopą
wolną od ryzyka (bowiem wycena odbywa się w świecie wolnym od
ryzyka).
jest stopą
wolną od ryzyka (bowiem wycena odbywa się w świecie wolnym od
ryzyka).
Niech ![]() oznacza prawdopodobieństwo wzrostu ceny aktywa w modelu
dwumianowym rynku w którym stopa oczekiwanego zwrotu wynosi
oznacza prawdopodobieństwo wzrostu ceny aktywa w modelu
dwumianowym rynku w którym stopa oczekiwanego zwrotu wynosi ![]() .
Wówczas, parametry modelu muszą być tak dobrane by
.
Wówczas, parametry modelu muszą być tak dobrane by
| (7.11) | |||
Równania (7.11) tworzą układ dwóch równań na trzy
niewiadome ![]() ,
, ![]() , oraz
, oraz ![]() . Musimy więc dołożyć dodatkowy
warunek, który umożliwi nam rozwiązanie układu. Przedstawimy dwa
rozwiązania, które uzyskamy przy dwóch różnych warunkach
dodatkowych.
. Musimy więc dołożyć dodatkowy
warunek, który umożliwi nam rozwiązanie układu. Przedstawimy dwa
rozwiązania, które uzyskamy przy dwóch różnych warunkach
dodatkowych.
![]() Rozwiązanie I (Model CRR – Cox, Ross,
Rubinstein)
Rozwiązanie I (Model CRR – Cox, Ross,
Rubinstein)
Warunek dodatkowy jest następujący – zakładamy, że
| (7.12) |
Ten warunek upraszcza tworzenie procesu cen aktywa na wielookresowym drzewie dwumianowym. Wówczas rozwiązanie układu równań (7.11), (7.12) ma następującą postać:
| (7.13) |
co wynika wprost z (7.11a), oraz
| (7.14) |
przy czym wielkości ![]() i
i ![]() spełniają równanie (7.11b) z
dokładnością od wyrażeń rzędu
spełniają równanie (7.11b) z
dokładnością od wyrażeń rzędu ![]() .
.
Uwagi
-
Można pokazać, że jeżeli
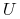 i
i 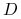 są określone równaniami (7.14), a
są określone równaniami (7.14), a
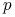 równaniem (7.13), to spełnianie warunku
(7.11b) nie zależy od wartości stopy
równaniem (7.13), to spełnianie warunku
(7.11b) nie zależy od wartości stopy 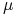 . To oznacza, że
w modelu dwumianowym zmienność aktywa jest taka sama niezależnie od
tego czy model opisuje świat realny czy świat wolny od ryzyka (ma to
związek z Twierdzeniem Girsanowa).
. To oznacza, że
w modelu dwumianowym zmienność aktywa jest taka sama niezależnie od
tego czy model opisuje świat realny czy świat wolny od ryzyka (ma to
związek z Twierdzeniem Girsanowa). -
Jeżeli zamiast przybliżonego równania (7.11b), do wyznaczania wartości współczynników
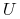 i
i 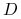 użyć dokładnego równania
użyć dokładnego równania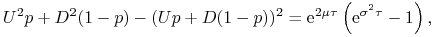
to wartości tych współczynników wyniosą

gdzie
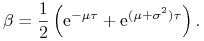
Można pokazać, że wówczas
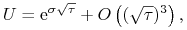
tak więc z dokładnością do wyrazów wyższego rzędu
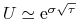 , tak jak w oryginalnym rozwiązaniu CRR.
, tak jak w oryginalnym rozwiązaniu CRR.
![]() Rozwiązanie II – Model ,,równych
prawdopodobieństw”
Rozwiązanie II – Model ,,równych
prawdopodobieństw”
Warunek dodatkowy jest następujący – przyjmujemy, że
| (7.15) |
Ten warunek upraszcza obliczanie wartości oczekiwanej przy obliczaniu ceny instrumentu pochodnego w wielookresowym modelu dwumianowym. Wówczas rozwiązanie układu równań (7.11), (7.15) ma następującą postać:
| (7.16) |
| (7.17) |
przy czym wielkości ![]() i
i ![]() spełniają równanie (7.11) z
dokładnością od wyrażeń rzędu
spełniają równanie (7.11) z
dokładnością od wyrażeń rzędu ![]() .
.
7.6. Zagadnienia i zadania na Ćwiczenia
W poniższych zadaniach przyjmijmy następujące definicje i określenia
-
Prosta stopa zwrotu
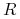 z aktywa
z aktywa 
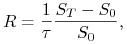
gdzie
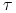 jest ułamkiem
roku dla okresu
jest ułamkiem
roku dla okresu ![[0,T]](wyklady/ifi/mi/mi591.png) .
. -
Stopa logarytmicznego zwrotu
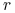 z aktywa
z aktywa 
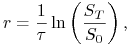
gdzie
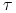 jest
ułamkiem roku dla okresu
jest
ułamkiem roku dla okresu ![[0,T]](wyklady/ifi/mi/mi591.png) .
. -
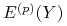 – wartość oczekiwana zmiennej
– wartość oczekiwana zmiennej 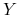 w modelu dwumianowym, w którym prawdopodobieństwo stanu ,,Up”
wynosi
w modelu dwumianowym, w którym prawdopodobieństwo stanu ,,Up”
wynosi 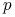 .
. -
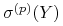 – odchylenie standardowe zmiennej
– odchylenie standardowe zmiennej 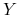 w modelu dwumianowym, w którym prawdopodobieństwo stanu ,,Up” wynosi
w modelu dwumianowym, w którym prawdopodobieństwo stanu ,,Up” wynosi 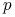 .
.
Ćwiczenie 7.1
Pokaż, że
-
(a)
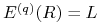 ,
, -
(b)
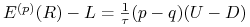 ,
, -
(c)
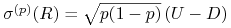 ,
, -
(d)
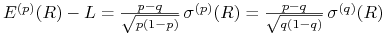 ,
,
gdzie ![]() jest stopą prostą opisującą kumulację kapitału na rachunku
bankowym – tzw. stopa wolna od ryzyka, a
jest stopą prostą opisującą kumulację kapitału na rachunku
bankowym – tzw. stopa wolna od ryzyka, a ![]() jest
prawdopodobieństwem (martyngałowym) w tym świecie wolnym od ryzyka.
jest
prawdopodobieństwem (martyngałowym) w tym świecie wolnym od ryzyka.
Ćwiczenie 7.2
Pokaż, że wartość aktywa ![]() w chwili
w chwili ![]() można wyrazić w
następujący sposób
można wyrazić w
następujący sposób
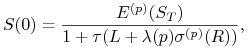 |
gdzie
Ćwiczenie 7.3
Pokaż, że
-
(a)
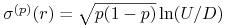
-
(b) W modelu CRR:
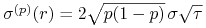
-
(c) W modelu równych prawdopodobieństw: