Zagadnienia
8. Model dwumianowy – wielookresowy
W modelu wielookresowym czas trwania instrumentu pochodnego, który
zapada w chwili ![]() , jest podzielony na
, jest podzielony na ![]() okresów o długości
okresów o długości
![]() każdy.
każdy.
Na rynku mamy dwa aktywa
-
obligację zerokuponową (rachunek bankowy na którym lokaty/depozyty są oprocentowane według stopy zerokuponowej)
 proces (zmienna) deterministyczna,
proces (zmienna) deterministyczna, -
aktywo obarczone ryzykiem, które nie przynosi dochodu
 proces stochastyczny.
proces stochastyczny.
![]() Proces wartości obligacji zerokuponowej
(rachunku bankowego) –
Proces wartości obligacji zerokuponowej
(rachunku bankowego) – ![]() , gdzie
, gdzie ![]() , a
, a ![]() .
Upraszczając notację będziemy pisać
.
Upraszczając notację będziemy pisać ![]() . Proces ten jest
zdefiniowany w następujący sposób
. Proces ten jest
zdefiniowany w następujący sposób
-
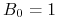 ,
, -
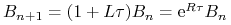 dla
dla 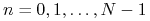 .
.
Tak więc zakładamy, że stopa procentowa jest stała w rozpatrywanym okresie czasu.
![]() Proces ceny aktywa ryzykownego –
Proces ceny aktywa ryzykownego – ![]() , gdzie
, gdzie
![]() , a
, a ![]() . Upraszczając notację będziemy pisać
. Upraszczając notację będziemy pisać
![]() . Proces ten jest zdefiniowany w następujący sposób
. Proces ten jest zdefiniowany w następujący sposób
-
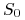 dane, znana wartość,
dane, znana wartość, -
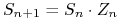 dla
dla 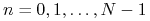 , gdzie
, gdzie
 są niezależnymi zmiennymi losowymi o
jednakowym rozkładzie
są niezależnymi zmiennymi losowymi o
jednakowym rozkładzie![Z_{n}=\left\{\begin{array}[]{ll}U,&\hbox{z prawdopodobieństwem $p$;}\\
D,&\hbox{z prawdopodobieństwem $1-p$.}\end{array}\right.](wyklady/ifi/mi/mi1006.png)
przy czym
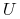 ,
, 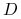 są dane oraz zakładamy, że
są dane oraz zakładamy, że 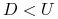 (te wielkości
są powiązane z innymi parametrami aktywa, w szczególności ze
zmiennością aktywa – patrz Wykład 7).
(te wielkości
są powiązane z innymi parametrami aktywa, w szczególności ze
zmiennością aktywa – patrz Wykład 7).
Drzewo dwumianowe
Proces ceny ryzykownego aktywa oraz wycena instrumentów pochodnych
będzie się odbywać na ![]() okresowym drzewie dwumianowym.
okresowym drzewie dwumianowym. ![]() ty
okres składa się z
ty
okres składa się z ![]() jednookresowych drzewek z których każde ma
swój wierzchołek w końcowych węzłach poprzedniego okresu. Te
jednookresowych drzewek z których każde ma
swój wierzchołek w końcowych węzłach poprzedniego okresu. Te ![]() jednookresowych drzewek ma swoje zakończenia w
jednookresowych drzewek ma swoje zakończenia w ![]() węzłach, które
są wierzchołkami jednookresowych drzewek w kolejnym okresie.
Będziemy zakładać, że drzewo rekombinuje się w tym sensie, że wzrost
ceny w okresie i spadek ceny w następnym okresie prowadzi do tej
samej wartości co spadek ceny w tym okresie i wzrost ceny w
następnym okresie – tak będzie gdy iloraz
węzłach, które
są wierzchołkami jednookresowych drzewek w kolejnym okresie.
Będziemy zakładać, że drzewo rekombinuje się w tym sensie, że wzrost
ceny w okresie i spadek ceny w następnym okresie prowadzi do tej
samej wartości co spadek ceny w tym okresie i wzrost ceny w
następnym okresie – tak będzie gdy iloraz ![]() będzie taki sam w
każdym okresie drzewa. Węzły drzewa będziemy oznaczać parą
będzie taki sam w
każdym okresie drzewa. Węzły drzewa będziemy oznaczać parą ![]() ,
gdzie
,
gdzie ![]() odpowiada chwili czasu
odpowiada chwili czasu ![]() , a
, a ![]() identyfikuje węzeł odpowiadający stanowi rynku, przy czym
identyfikuje węzeł odpowiadający stanowi rynku, przy czym ![]() oznacza liczbę wzrostów ceny na drodze od wierzchołka drzewa do tego
węzła. Wierzchołek drzewa oznaczamy parą
oznacza liczbę wzrostów ceny na drodze od wierzchołka drzewa do tego
węzła. Wierzchołek drzewa oznaczamy parą ![]() . Tak więc cena
aktywa w chwili
. Tak więc cena
aktywa w chwili ![]() w
w ![]() węźle wynosi
węźle wynosi
Strategia inwestycyjna to portfel
gdzie
-
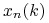 – ilość pieniędzy zainwestowana w obligację
zerokuponową (rachunek bankowy) w węźle
– ilość pieniędzy zainwestowana w obligację
zerokuponową (rachunek bankowy) w węźle 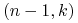 trzymana do chwili
trzymana do chwili
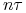 ,
,
-
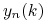 – ilość aktywa ryzykownego w portfelu stworzonym w węźle
– ilość aktywa ryzykownego w portfelu stworzonym w węźle
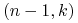 trzymana do chwili
trzymana do chwili 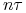 .
.
Ponadto, w celu zapewnienia spójności formuł definiujemy ![]() .
.
Wielkości ![]() są zmiennymi losowymi, tak więc możemy mówić, że
strategia inwestycyjna jest procesem stochastycznym. Skład portfela
są zmiennymi losowymi, tak więc możemy mówić, że
strategia inwestycyjna jest procesem stochastycznym. Skład portfela
![]() zależy od całej informacji o stanie rynku dostępnej do chwili
zależy od całej informacji o stanie rynku dostępnej do chwili
![]() (włącznie)
(włącznie)![]()
![]() jest tzw. procesem
prognozowalnym.
jest tzw. procesem
prognozowalnym.
Proces wartości strategii. W chwili ![]() portfel
portfel ![]() ma
wartość
ma
wartość
gdzie ![]() oraz
oraz
![]() .
.
Strategia (portfel) ![]() jest samofinansująca(y) się wtedy i
tylko wtedy gdy dla każdego
jest samofinansująca(y) się wtedy i
tylko wtedy gdy dla każdego ![]() zachodzi
zachodzi
Ten warunek oznacza, że zmiana składu portfela w chwili czasu
![]() odbywa się bez dopływu gotówki do portfela lub odpływu
gotówki z portfela.
odbywa się bez dopływu gotówki do portfela lub odpływu
gotówki z portfela.
Samofinansujący się portfel ![]() jest strategią arbitrażową, jeżeli
jest strategią arbitrażową, jeżeli
-
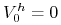 ,
, -
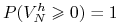 ,
, -
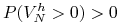 .
.
Tak jak poprzednio w przypadku modelu jednookresowego, model nie dopuszcza arbitrażu wtedy i tylko wtedy gdy
| (8.1) |
Dowód tego faktu podamy w dalszej części wykładu (patrz Twierdzenie 8.3).
Na razie załóżmy, że warunek ![]() jest spełniony. Wówczas, możemy
określić miarę martyngałową
jest spełniony. Wówczas, możemy
określić miarę martyngałową ![]() , taką, że
, taką, że
a prawdopodobieństwa martyngałowe dane są wzorami
| (8.2) |
Rozważamy europejskie instrumenty pochodne ![]() , których wartość
wypłaty w chwili zapadalności dana jest przez pewną funkcję
, których wartość
wypłaty w chwili zapadalności dana jest przez pewną funkcję ![]() zmiennej
zmiennej ![]()
Podobnie jak w przypadku modelu
jednookresowego, instrument pochodny ![]() jest osiągalny
jeśli istnieje samofinansujący się portfel
jest osiągalny
jeśli istnieje samofinansujący się portfel ![]() replikujący
replikujący ![]() ,
to znaczy taki, że
,
to znaczy taki, że
Model rynku jest zupełny jeżeli każdy instrument pochodny da się zreplikować samofinansującym się portfelem utworzonym z aktywów dostępnych na tym rynku.
Zasada wyceny instrumentów pochodnych jest analogiczna jak w
przypadku modelu jednookresowego. Jeżeli ![]() jest osiągalny, to
sprawiedliwa cena tego instrumentu, tj. cena, która uniemożliwia
przeprowadzenie arbitrażu, w chwili
jest osiągalny, to
sprawiedliwa cena tego instrumentu, tj. cena, która uniemożliwia
przeprowadzenie arbitrażu, w chwili ![]() dana jest wzorem
dana jest wzorem
gdzie ![]() jest samofinansującą się
strategią replikującą
jest samofinansującą się
strategią replikującą ![]() .
.
Poniższe twierdzenie opisuje algorytm wyznaczania portfela replikującego i wyznaczania ceny instrumentu pochodnego. Wnioskiem z tego twierdzenia jest również zupełność rynku.
Twierdzenie 8.1
Niech ![]() będzie europejskim instrumentem pochodnym, zapadalnym w
chwili
będzie europejskim instrumentem pochodnym, zapadalnym w
chwili ![]() , którego wartość wypłaty dana jest funkcją
, którego wartość wypłaty dana jest funkcją
![]() .
. ![]() można zreplikować samofinansującym się
portfelem
można zreplikować samofinansującym się
portfelem ![]() , którego wartości obliczamy następującym algorytmem
rekurencyjnym
, którego wartości obliczamy następującym algorytmem
rekurencyjnym
| (8.3) |
oraz dla ![]() ,
,
| (8.4) |
a ![]() i
i ![]() są określone w (8.2). Skład portfela
replikującego dany jest następującymi wzorami
są określone w (8.2). Skład portfela
replikującego dany jest następującymi wzorami
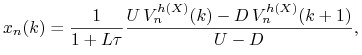 |
(8.5) |
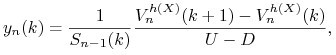 |
(8.6) |
gdzie ![]() a
a ![]() .
.
W szczególności, cena instrumentu pochodnego ![]() w
w ![]() wynosi
wynosi ![]() . Wzór na tę cenę zawarty jest następującym
twierdzeniu.
. Wzór na tę cenę zawarty jest następującym
twierdzeniu.
Twierdzenie 8.2
Sprawiedliwa cena europejskiego instrumentu pochodnego ![]() w chwili
w chwili
![]() dana jest wzorem
dana jest wzorem
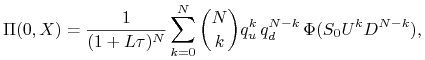 |
(8.7) |
który możemy zapisać w postaci
| (8.8) |
gdzie
![]() jest wolną od ryzyka miarą na przestrzeni stanów rynku w
chwili
jest wolną od ryzyka miarą na przestrzeni stanów rynku w
chwili ![]() :
:
Twierdzenie 8.3
Wielookresowy model rynku nie dopuszcza arbitrażu wtedy i tylko wtedy gdy
| (8.9) |
Jeżeli arbitraż nie jest możliwy, to nierówność ![]() uzyskujemy z
analogicznego twierdzenia dla modelu jednookresowego. Załóżmy teraz,
że nierówności
uzyskujemy z
analogicznego twierdzenia dla modelu jednookresowego. Załóżmy teraz,
że nierówności ![]() zachodzą. Niech
zachodzą. Niech ![]() będzie samofinansującym
się portfelem, który spełnia warunki
będzie samofinansującym
się portfelem, który spełnia warunki
-
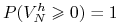 ,
, -
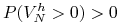 .
.
Wówczas, z twierdzenia (8.3) wynika, że
![]() Tak więc
Tak więc ![]() nie może
być portfelem arbitrażowym.
nie może
być portfelem arbitrażowym.
8.1. Podsumowanie – algorytm wyceny na drzewie dwumianowym
Dla
-
europejskiego instrumentu pochodnego,
-
o wypłacie niezależnej od drogi,
-
którego instrument podstawowy nie daje dochodu w czasie trwania kontraktu.
Na podstawie danych
-
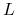 – stopy procentowej (wolnej od ryzyka),
– stopy procentowej (wolnej od ryzyka), -
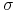 – zmienności cen instrumentu podstawowego,
– zmienności cen instrumentu podstawowego,
wyznaczamy
-
współczynniki
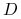 i
i 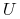 ,
, -
odpowiednie wartości prawdopodobieństw martyngałowych
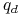 oraz
oraz 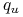 .
.
![]() Etap pierwszy: wyznaczenie procesu cen
instrumentu podstawowego na drzewie
Etap pierwszy: wyznaczenie procesu cen
instrumentu podstawowego na drzewie
Dla ![]() wyznaczamy wartości instrumentu podstawowego w
wyznaczamy wartości instrumentu podstawowego w
![]() węzłach każdej warstwy czasowej
węzłach każdej warstwy czasowej ![]() korzystając z wzoru
korzystając z wzoru
W przypadku instrumentu europejskiego niezależnego od drogi
potrzebujemy wartości instrumentu podstawowego tylko w chwili
![]() .
.
![]() Etap drugi: indukcja wstecz – wyznaczenie
wartości instrumentu pochodnego na drzewie
Etap drugi: indukcja wstecz – wyznaczenie
wartości instrumentu pochodnego na drzewie
Obliczamy wartość wypłaty z instrumentu pochodnego w chwili
zapadalności kontraktu ![]()
Następnie, obliczamy kolejno dla ![]()
Wartość instrumentu pochodnego
![]() w chwili
w chwili ![]() wynosi
wynosi ![]() .
.
Uwaga 8.1
Algorytm dwumianowy opisany w twierdzeniu 8.1
(lub w powyższym podsumowaniu) można przenieść na przypadek
instrumentów pochodnych typu amerykańskiego. Niech wartość wypłaty
takiego instrumentu w chwili ![]() będzie dana wzorem
będzie dana wzorem
![]() . Taki instrument jest wyceniamy również przez
konstrukcję i wycenę strategii replikującej. Wyznaczając wartości
strategii replikującej instrument amerykański musimy dodatkowo
sprawdzać w poszczególnych węzłach czy optymalne jest wcześniejsze
wykonanie. W tym celu wystarczy zmodyfikować wzór (8.3) w
następujący sposób:
. Taki instrument jest wyceniamy również przez
konstrukcję i wycenę strategii replikującej. Wyznaczając wartości
strategii replikującej instrument amerykański musimy dodatkowo
sprawdzać w poszczególnych węzłach czy optymalne jest wcześniejsze
wykonanie. W tym celu wystarczy zmodyfikować wzór (8.3) w
następujący sposób:
| (8.10) |
gdzie ![]() , oraz
, oraz ![]()
8.2. Dalsze uogólnienia i rozszerzenia algorytmu dwumianowego
![]() Uwzględnienie struktury stóp procentowych
Uwzględnienie struktury stóp procentowych
Niech ![]() oznacza stopę forward kapitalizowaną w sposób ciągły na
okres czasu
oznacza stopę forward kapitalizowaną w sposób ciągły na
okres czasu ![]() . Wówczas, konstruując drzewo
dwumianowe należy uwzględnić następujące modyfikacje.
. Wówczas, konstruując drzewo
dwumianowe należy uwzględnić następujące modyfikacje.
-
W modelu CRR wartości współczynników
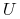 i
i 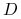 są takie same w każdym
podokresie drzewa (bo zależą tylko od zmienności
są takie same w każdym
podokresie drzewa (bo zależą tylko od zmienności 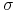 – patrz
wzór (7.3)), natomiast prawdopodobieństwa martyngałowe
– patrz
wzór (7.3)), natomiast prawdopodobieństwa martyngałowe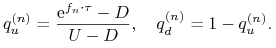
(8.11) będą się zmieniać w kolejnych podokresach drzewa.
-
W modelu ,,równych prawdopodobieństw” zmieniać się będą w kolejnych podokresach wartości współczynników
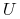 i
i 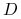 ; mianowicie wyniosą
one
; mianowicie wyniosą
one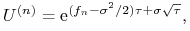
(8.12) 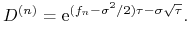
Prawdopodobieństwa martyngałowe będą oczywiście takie same (równe
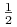 ).
).
W obu metodach, mimo tych modyfikacji, drzewo dwumianowe w dalszym
ciągu się rekombinuje, bowiem iloraz ![]() ma stałą wartość w każdym
z podokresów drzewa. Algorytm wyceny instrumentów pochodnych
sformułowany w twierdzeniu 8.1 w zasadzie pozostaje bez
zmian – należy jedynie pamiętać o uzmiennieniu odpowiednich
parametrów w formułach (8.4)–(8.6). W
szczególności, zamiast czynnika dyskontowego postaci
ma stałą wartość w każdym
z podokresów drzewa. Algorytm wyceny instrumentów pochodnych
sformułowany w twierdzeniu 8.1 w zasadzie pozostaje bez
zmian – należy jedynie pamiętać o uzmiennieniu odpowiednich
parametrów w formułach (8.4)–(8.6). W
szczególności, zamiast czynnika dyskontowego postaci ![]() ,
który nie zależy od podokresu, należy użyć czynników które są
wyznaczane na postawie stóp forward, na przykład mających postać
,
który nie zależy od podokresu, należy użyć czynników które są
wyznaczane na postawie stóp forward, na przykład mających postać
![]() .
.
Następne modyfikacje polegają na uwzględnieniu dochodów przynoszonych przez aktywo. Rozpatrzmy trzy przypadki:
-
aktywo ryzykowne przynosi ,,ciągły” dochód,
-
aktywo ryzykowne przynosi ,,dyskretny” dochód, który jest wyrażony jako procent bieżącej ceny aktywa,
-
aktywo ryzykowne przynosi ,,dyskretny” dochód, który jest przedstawiony jako strumień płatności.
![]() Aktywo ryzykowne przynosi ,,ciągły” dochód
(np. indeks giełdowy, kurs walutowy)
Aktywo ryzykowne przynosi ,,ciągły” dochód
(np. indeks giełdowy, kurs walutowy)
Niech ![]() oznacza stopę dochodu kapitalizowaną w sposób ciągły.
Modyfikacje algorytmu dwumianowego polegają na zastąpieniu w
odpowiednich wyrażeniach stopy wolnej od ryzyka
oznacza stopę dochodu kapitalizowaną w sposób ciągły.
Modyfikacje algorytmu dwumianowego polegają na zastąpieniu w
odpowiednich wyrażeniach stopy wolnej od ryzyka ![]() (lub ogólniej
stóp forward
(lub ogólniej
stóp forward ![]() ) przez różnicę tej stopy i stopy dochodu, czyli
przez
) przez różnicę tej stopy i stopy dochodu, czyli
przez ![]() (lub odpowiednio przez
(lub odpowiednio przez ![]() ). I tak,
). I tak,
-
W modelu CRR wartości współczynników
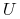 i
i 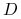 pozostają bez zmian
(bo zależą tylko od zmienności
pozostają bez zmian
(bo zależą tylko od zmienności 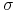 – patrz wzór
(7.3)), natomiast prawdopodobieństwa martyngałowe wynoszą
– patrz wzór
(7.3)), natomiast prawdopodobieństwa martyngałowe wynoszą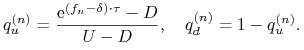
(8.13) -
W modelu ,,równych prawdopodobieństw” wartości współczynników
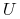 i
i 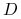 wynoszą
wynoszą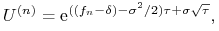
(8.14) 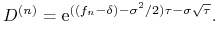
Prawdopodobieństwa martyngałowe będą oczywiście takie same (równe
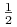 ).
).
W przypadku, gdy ![]() jest kursem walutowym podanym jako ilość waluty
jest kursem walutowym podanym jako ilość waluty
![]() za jednostkę waluty
za jednostkę waluty ![]() ,
, ![]() jest stopą
waluty
jest stopą
waluty ![]() , a
, a ![]() jest stopą waluty
jest stopą waluty ![]() .
.
![]() Aktywo ryzykowne przynosi ,,dyskretny”
dochód, który jest wyrażony jako procent bieżącej ceny aktywa
Aktywo ryzykowne przynosi ,,dyskretny”
dochód, który jest wyrażony jako procent bieżącej ceny aktywa
Zakładamy, że aktywo daje dochód w terminach zgodnych z podziałem
czasu trwania instrumentu pochodnego na okresy drzewa. Wielkość tego
dochodu jest wyrażona jako procent ceny bieżącej aktywa. Dokładniej,
załóżmy że w chwili ![]() aktywo wypłaca dochód w wysokości
aktywo wypłaca dochód w wysokości
![]() , gdzie
, gdzie ![]() jest ceną aktywa w chwili
jest ceną aktywa w chwili ![]() , a
, a ![]() określa procentową wysokość tego dochodu. Zakładamy, że wypłata
tego dochodu powoduje spadek wartości ceny bieżącej o wartość
wypłaty. Czyli tuż po wypłacie dochodu aktywo ma wartość
określa procentową wysokość tego dochodu. Zakładamy, że wypłata
tego dochodu powoduje spadek wartości ceny bieżącej o wartość
wypłaty. Czyli tuż po wypłacie dochodu aktywo ma wartość ![]() .
Uwzględnienie takiego mechanizmu wypłat dochodu przy tworzeniu
drzewa dwumianowego jest proste. Mianowicie, generując proces cen
aktywa na drzewie, tak długo jak aktywo nie daje dochodu postępujemy
według algorytmu dla aktywa nieprzynoszącego dochodu, po czym w
momencie wypłaty dochodu w każdym węźle drzewa warstwy czasowej
.
Uwzględnienie takiego mechanizmu wypłat dochodu przy tworzeniu
drzewa dwumianowego jest proste. Mianowicie, generując proces cen
aktywa na drzewie, tak długo jak aktywo nie daje dochodu postępujemy
według algorytmu dla aktywa nieprzynoszącego dochodu, po czym w
momencie wypłaty dochodu w każdym węźle drzewa warstwy czasowej
![]() obniżamy ceny aktywa o wartość
obniżamy ceny aktywa o wartość ![]() (wartość
(wartość ![]() zastępujemy przez
zastępujemy przez ![]() dla
dla ![]() ). Dalej, do
następnego momentu wypłaty, postępujemy znów według algorytmu dla
aktywa nieprzynoszącego dochodu startując w chwili
). Dalej, do
następnego momentu wypłaty, postępujemy znów według algorytmu dla
aktywa nieprzynoszącego dochodu startując w chwili ![]() z
wartości
z
wartości ![]() . Wartości współczynników
. Wartości współczynników ![]() i
i ![]() oraz
prawdopodobieństw martyngałowych są takie same jak dla aktywa
nieprzynoszącego dochodu. Należy zauważyć, że ,,multiplikatywność”
dochodu powoduje iż drzewo w dalszym ciągu się rekombinuje.
oraz
prawdopodobieństw martyngałowych są takie same jak dla aktywa
nieprzynoszącego dochodu. Należy zauważyć, że ,,multiplikatywność”
dochodu powoduje iż drzewo w dalszym ciągu się rekombinuje.
Aktywo ryzykowne przynosi ,,dyskretny” dochód będący strumieniem płatności (np. akcja z dywidendą)
Zakładamy że aktywo daje dochód w terminach zgodnych z podziałem czasu trwania instrumentu pochodnego na okresy drzewa. Wówczas, konstruując proces ceny aktywa na drzewie należy pamiętać o tym że po wypłacie dochodu cena aktywa skokowo spada o wielkość wypłaty. Obniżenie ceny aktywa w momencie wypłat dochodu o stałe wartości powoduje iż drzewo przestaje się rekombinować. Sposób obejścia tego problemu jest następujący.
-
Obliczamy
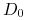 – wartość bieżącą (na chwilę 0) strumienia wszystkich
przyszłych (do chwili
– wartość bieżącą (na chwilę 0) strumienia wszystkich
przyszłych (do chwili  ) dochodów.
) dochodów. -
Tworzymy rekombinujące się drzewo procesu cen aktywa (,,obdartego” z części deterministycznej – tj. z wartości znanych z góry dochodów) startując z wartości
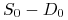 i używając współczynników
i używając współczynników 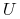 i
i 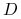 jak dla aktywa niepłacącego dochodu.
jak dla aktywa niepłacącego dochodu. -
Tak otrzymane drzewo modyfikujemy dodając z powrotem składowe odpowiadające dochodom generowanym przez aktywo. Mianowicie do cen aktywa w chwili
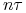 utworzonych w kroku (2) dodajemy wartość bieżącą na chwilę
utworzonych w kroku (2) dodajemy wartość bieżącą na chwilę
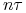 wszystkich przyszłych (względem chwili
wszystkich przyszłych (względem chwili 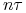 ) dochodów
generowanych przez aktywo. W szczególności, po tej modyfikacji
proces cen ponownie startuje z ceny bieżącej aktywa
) dochodów
generowanych przez aktywo. W szczególności, po tej modyfikacji
proces cen ponownie startuje z ceny bieżącej aktywa 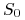 oraz
uwzględnia skokowe zmiany wartości aktywa będące konsekwencjami
wypłat dochodu.
oraz
uwzględnia skokowe zmiany wartości aktywa będące konsekwencjami
wypłat dochodu.
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 8.1
Wycenić opcję sprzedaży (put) akcji na dwuokresowym drzewie dwumianowym przy następujących danych:
-
bieżąca cena akcji wynosi
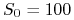 ,
, -
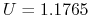 ,
, 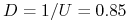 ,
, -
czas trwania opcji wynosi 2 miesiące (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla jednomiesięcznych lokat/depozytów w każdym okresie wynosi
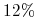 (pa),
(pa), -
cena wykonania wynosi
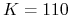 .
.
Wycenę przeprowadź w dwóch przypadkach: (a) opcji europejskiej, (b) opcji amerykańskiej.
Ćwiczenie 8.2
Wycenić europejską opcję kupna (call) akcji na trzyokresowym drzewie dwumianowym przy następujących danych:
-
bieżąca cena akcji wynosi
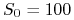 ,
, -
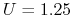 ,
, 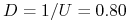 ,
, -
czas trwania opcji wynosi 9 miesięcy (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla trzymiesięcznych lokat/depozytów wynosi 8% (pa), dla sześciomiesięcznych 9%, a dla dziewięciomiesięcznych 10%.
-
cena wykonania wynosi
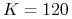 .
.
Ćwiczenie 8.3
Rozpatrzmy europejski instrument pochodny o następującej funkcji wypłaty
gdzie ![]() jest
stopą zwrotu z akcji w okresie
jest
stopą zwrotu z akcji w okresie ![]() . Wyceń ten instrument na
trzyokresowym drzewie dwumianowym przy następujących danych:
. Wyceń ten instrument na
trzyokresowym drzewie dwumianowym przy następujących danych:
-
bieżąca cena akcji wynosi
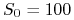 ,
, -
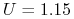 ,
, 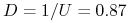 ,
, -
czas trwania opcji wynosi 9 miesięcy (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla trzymiesięcznych lokat/depozytów w każdym okresie wynosi 8% (pa),
-
cena wykonania wynosi
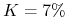 .
.
Ćwiczenie 8.4
Wycenić europejską opcję sprzedaży (put) akcji na dwuokresowym drzewie dwumianowym przy następujących danych
-
bieżąca cena akcji wynosi
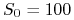 ,
, -
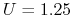 ,
, 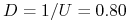 ,
, -
czas trwania opcji wynosi 6 miesięcy (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla trzymiesięcznych lokat/depozytów w każdym okresie wynosi 8% (pa),
-
cena wykonania wynosi
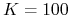 , przy czym jeśli na końcu trzeciego
miesiąca cena akcji spadnie poniżej 85, to cena wykonania zostanie
obniżona do
, przy czym jeśli na końcu trzeciego
miesiąca cena akcji spadnie poniżej 85, to cena wykonania zostanie
obniżona do 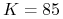 .
.
Ćwiczenie 8.5
Rozpatrzmy europejską opcję kupna akcji. Cena wykonania opcji ![]() zależy od ceny akcji w chwili zapadalności opcji w następujący
sposób:
zależy od ceny akcji w chwili zapadalności opcji w następujący
sposób:
![K=\left\{\begin{array}[]{ll}30,&\hbox{gdy $S_{T}<30$,}\\
S_{T},&\hbox{gdy $30\leq S_{T}\leq 60$,}\\
60+\frac{1}{10}(S_{T}-60),&\hbox{gdy $60<S_{T}$.}\end{array}\right.](wyklady/ifi/mi/mi1058.png) |
Wyceń ten instrument na trzyokresowym drzewie dwumianowym przy następujących danych:
-
bieżąca cena akcji wynosi
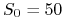 ,
, -
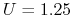 ,
, 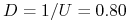 ,
, -
czas trwania opcji wynosi 9 miesięcy (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla trzymiesięcznych lokat/depozytów w każdym okresie wynosi 8% (pa).
Ćwiczenie 8.6
Rozpatrzmy europejski instrument pochodny o następującej funkcji wypłaty:
Wyznacz wartość ![]() , tak by cena tego instrumentu pochodnego przy
następujących danych:
, tak by cena tego instrumentu pochodnego przy
następujących danych:
-
bieżąca cena akcji wynosi
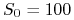 ,
, -
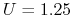 ,
, 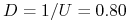 ,
, -
czas trwania opcji wynosi 9 miesięcy (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla trzymiesięcznych lokat/depozytów w każdym okresie wynosi 8% (pa),
-
cena wykonania wynosi
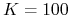 ,
,
wynosiła zero. Posłuż się trzyokresowym drzewem dwumianowym.
Ćwiczenie 8.7
Rozpatrzmy europejski instrument pochodny o następującej funkcji wypłaty:
Wyznacz cenę tego instrumentu pochodnego w zależności od
parametru ![]() przy następujących danych:
przy następujących danych:
-
bieżąca cena akcji wynosi
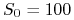 ,
, -
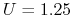 ,
, 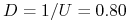 ,
, -
czas trwania opcji wynosi 9 miesięcy (można przyjąć że 1 miesiąc = 1/12 roku),
-
stopa procentowa dla trzymiesięcznych lokat/depozytów w każdym okresie wynosi 8% (pa),
-
cena wykonania wynosi
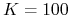 .
.
Posłuż się trzyokresowym drzewem dwumianowym.
Ćwiczenie 8.8
Rozpatrzmy europejski instrument pochodny o następującej funkcji wypłaty
Wyznacz cenę tego instrumentu pochodnego przy następujących danych:
-
bieżąca cena akcji wynosi
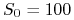 ,
, -
zmienność akcji wynosi
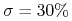 ,
, -
czas trwania opcji wynosi 9 miesięcy (można przyjąć, że 1 miesiąc = 1/12 roku),
-
struktura stóp procentowych jest płaska i stopa procentowa kapitalizowana w sposób ciągły wynosi 6% (pa),
-
cena wykonania wynosi
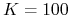 .
.
Posłuż się trzyokresowym drzewem dwumianowym.
Ćwiczenie 8.9
Rozpatrzmy europejską trzymiesięczną opcję kupna ![]() mln USD po
cenie
mln USD po
cenie ![]() PLN za 1 USD. Wyznacz cenę tej opcji przy
następujących danych:
PLN za 1 USD. Wyznacz cenę tej opcji przy
następujących danych:
-
bieżący kurs wymiany wynosi
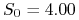 PLN za 1 USD,
PLN za 1 USD, -
zmienność kursu wynosi
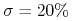 ,
, -
struktura stóp procentowych dla obu walut jest płaska i stopy procentowe kapitalizowane w sposób ciągły wynoszą: dla USD –
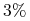 (pa), a dla PLN –
(pa), a dla PLN – 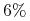 (pa).
(pa).
Posłuż się trzyokresowym drzewem dwumianowym. Dla uproszczenia obliczeń możesz przyjąć że 1 miesiąc = 1/12 roku.
Ćwiczenie 8.10
(a) Rozpatrzmy europejską trzymiesięczną azjatycką opcję kupna
![]() mln USD po cenie
mln USD po cenie ![]() PLN za 1 USD, w której średnia
arytmetyczna występująca w funkcji wypłaty
PLN za 1 USD, w której średnia
arytmetyczna występująca w funkcji wypłaty
jest postaci
Wyznacz cenę tej opcji przy następujących danych:
-
bieżący kurs wymiany wynosi
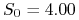 PLN za 1 USD,
PLN za 1 USD, -
zmienność kursu wynosi
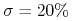 ,
, -
struktura stóp procentowych dla obu walut jest płaska i stopy procentowe kapitalizowane w sposób ciągły wynoszą: dla USD – 3% (pa), a dla PLN – 6% (pa).
Posłuż się trzyokresowym drzewem dwumianowym. Dla uproszczenia obliczeń możesz przyjąć że 1 miesiąc = 1/12 roku. Porównaj cenę tej opcji z ceną opcji waniliowej obliczoną w Zadaniu 8.9.
(b) Przy tych samych danych wyceń europejską trzymiesięczną azjatycką opcję kupna, w której cena wykonania jest średnią arytmetyczną cen instrumentu podstawowego, to jest opcję o następującej funkcji wypłaty:
Porównaj cenę tej opcji z ceną opcji waniliowej obliczoną w Zadaniu 8.9.
Ćwiczenie 8.11
Uzasadnij wzory na prawdopodobieństwo martyngałowe oraz wycenę
instrumentów pochodnych w przypadku modelu dwumianowego dla
instrumentów pochodnych na kurs walutowy ![]() wyrażony jako ilość
waluty
wyrażony jako ilość
waluty ![]() za jednostkę waluty
za jednostkę waluty ![]() (ogólniej
na aktywo płacące ciągłą dywidendę). W tym modelu mamy trzy aktywa:
dwa aktywa wolne od ryzyka odpowiadające rachunkom pieniężnym w
walucie
(ogólniej
na aktywo płacące ciągłą dywidendę). W tym modelu mamy trzy aktywa:
dwa aktywa wolne od ryzyka odpowiadające rachunkom pieniężnym w
walucie ![]() oraz w walucie
oraz w walucie ![]() odpowiednio,
oraz aktywo ryzykowne – kurs walutowy
odpowiednio,
oraz aktywo ryzykowne – kurs walutowy ![]() . Wyznacz na drzewie
jednookresowym portfel replikujący instrument pochodny i przedstaw
jego cenę jako zdyskontowaną wartość oczekiwaną wypłaty w
odpowiedniej mierze martyngałowej.
. Wyznacz na drzewie
jednookresowym portfel replikujący instrument pochodny i przedstaw
jego cenę jako zdyskontowaną wartość oczekiwaną wypłaty w
odpowiedniej mierze martyngałowej.




