Zagadnienia
- 9.1 Model dynamiki cen aktywa
- 9.2 Rozkład logarytmicznej stopy zwrotu
- 9.3 Zasada wyceny instrumentów pochodnych w modelu ciągłym
- 9.4 Wycena instrumentów pochodnych w modelu Blacka-Scholesa
- 9.5 Formuły Blacka-Scholesa dla europejskich opcji waniliowych
- 9.6 Proste uogólnienia formuł Blacka-Scholesa
- 9.7 Wycena instrumentów pochodnych metodą Monte Carlo
- Zagadnienia i zadania na Ćwiczenia
9. Model Blacka-Scholesa
Model dwumianowy był prostym modelem za pomocą którego opisaliśmy proces stochastyczny ceny aktywa. Był to tak zwany model dyskretny, bowiem zmienna czasowa przyjmowała wartości dyskretne oraz wartości przyjmowane przez ceny aktywa w tych chwilach czasu tworzyły zbiory dyskretne. Mimo swojej prostoty, model ten przy dostatecznie dużej liczbie kroków czasowych na danym odcinku czasu (to jest, dla danego czasu trwania instrumentu) daje stosunkowo dokładną wycenę szerokiej klasy instrumentów pochodnych. Gdy liczba kroków czasowych na ustalonym odcinku czasu dąży do nieskończoności (długość okresu na drzewie dwumianowym dąży do zera), model dwumianowy przechodzi w model ciągły. W wyniku przejścia granicznego rozkład dwumianowy ,,przechodzi” w rozkład log-normalny, natomiast zasada wyceny instrumentów pochodnych w modelu ciągłym pozostaje taka sama jak w modelu dyskretnym.
9.1. Model dynamiki cen aktywa
Będziemy zakładać, że ![]() spełnia następujące stochastyczne równanie
spełnia następujące stochastyczne równanie
| (9.1) |
gdzie
-
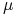 jest stopą zwrotu
jest stopą zwrotu  (współczynnikiem dryfu),
(współczynnikiem dryfu), -
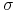 jest zmiennością
jest zmiennością  (współczynnikiem dyfuzji),
(współczynnikiem dyfuzji), -
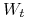 jest tak zwanym procesem Wienera.
jest tak zwanym procesem Wienera.
W naszym prostym modelu o ![]() i
i ![]() zakładamy, że są stałe,
to jest nie zależą od czasu
zakładamy, że są stałe,
to jest nie zależą od czasu ![]() i procesu
i procesu ![]() . Równanie
(9.1) jest szczególnym przypadkiem ogólniejszej klasy
równań stochastycznych postaci
. Równanie
(9.1) jest szczególnym przypadkiem ogólniejszej klasy
równań stochastycznych postaci
| (9.2) |
gdzie ![]() i
i ![]() są
procesami o odpowiednich własnościach, które często zależą od
są
procesami o odpowiednich własnościach, które często zależą od ![]() i
procesu
i
procesu ![]() . Nasz prosty przypadek uzyskujemy kładąc w
(9.2)
. Nasz prosty przypadek uzyskujemy kładąc w
(9.2) ![]() oraz
oraz ![]() i zamieniając
i zamieniając ![]() na
na ![]() .
.
Proces Wienera ![]() to proces stochastyczny o następujących
własnościach:
to proces stochastyczny o następujących
własnościach:
-
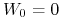 ,
, -
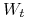 ma niezależne przyrosty, to znaczy, dla każdych
ma niezależne przyrosty, to znaczy, dla każdych
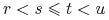 zmienne losowe
zmienne losowe 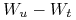 i
i 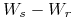 są niezależne,
są niezależne, -
dla każdych
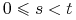
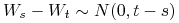 ,
, -
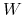 ma ciągłe trajektorie (z prawdopodobieństwem 1).
ma ciągłe trajektorie (z prawdopodobieństwem 1).
W szczególności z tych warunków wynika, że
oraz
Uwaga 9.1
Wbrew pozorom równanie (9.2) (ani (9.1)) nie jest równaniem różniczkowym. A to dlatego że pochodna trajektorii procesu Wienera nie istnieje (z prawdopodobieństwem 1 są one nigdzie nieróżniczkowalne). Tak naprawdę równanie (9.2) należy rozumieć jako równanie całkowe
| (9.3) |
gdzie druga całka jest tak zwaną całką stochastyczną Itô, która jest już dobrze zdefiniowanym obiektem matematycznym.
Nie podamy definicji całki stochastycznej Itô (proszę poczekać cierpliwie na wykład z procesów stochastycznych – zainteresowanym przystępnym wprowadzeniem do rachunku stochastycznego polecam podręcznik Steven'a E. Shreve'a Stochastic Calculus for Finance II (Springer 2004)[2]). Zadowolimy się natomiast wybranymi szczególnymi technikami rachunku stochastycznego, które powinny nam wystarczyć dla naszych rozważań. Mamy następujący
Lemat 9.1
Dla deterministycznej funkcji ![]() całkowalnej z kwadratem,
całkowalnej z kwadratem,
Będą nas również interesować funkcje postaci ![]() gdzie
gdzie ![]() jest procesem spełniającym równanie (9.2). W szczególności
chcielibyśmy wiedzieć jakie równanie stochastyczne spełnia proces
jest procesem spełniającym równanie (9.2). W szczególności
chcielibyśmy wiedzieć jakie równanie stochastyczne spełnia proces
![]() . Na to pytanie odpowiada następujący
. Na to pytanie odpowiada następujący
Lemat 9.2 (Lemat Itô)
Załóżmy, że proces ![]() spełnia równanie stochastyczne
spełnia równanie stochastyczne
| (9.4) |
gdzie ![]() i
i ![]() są
adaptowalnymi procesami (o odpowiednich własnościach by całki miały
sens). Niech
są
adaptowalnymi procesami (o odpowiednich własnościach by całki miały
sens). Niech ![]() . Wówczas proces
. Wówczas proces
![]() spełnia następujące równanie
spełnia następujące równanie
| (9.5) |
W szczególnym przypadku, gdy ![]() oraz
oraz ![]() , to
jest gdy
, to
jest gdy ![]() spełnia równanie (9.1), teza Lematu Itô
przyjmuje następującą postać:
spełnia równanie (9.1), teza Lematu Itô
przyjmuje następującą postać:
Przykłady zastosowania Lematu Itô:
-
Niech
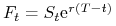 będzie ceną kontraktu Forward (ceną
teoretyczną kontraktu Futures) na aktywo, które nie przynosi dochodu
w trakcie trwania kontraktu
będzie ceną kontraktu Forward (ceną
teoretyczną kontraktu Futures) na aktywo, które nie przynosi dochodu
w trakcie trwania kontraktu ![[t,T]](wyklady/ifi/mi/mi188.png) . Wówczas
. Wówczas 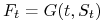 , gdzie
, gdzie
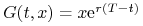 . Jeżeli cena aktywa
. Jeżeli cena aktywa  spełnia
(9.1), to na mocy lematu Itô, proces
spełnia
(9.1), to na mocy lematu Itô, proces 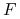 spełnia
następujące równanie
spełnia
następujące równanie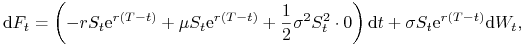
które po uporządkowaniu przyjmuje następującą postać
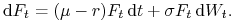
(9.6) -
Korzystając z Lematu Itô obliczymy całkę stochastyczną
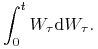
Niech
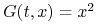 . Rozpatrzmy proces
. Rozpatrzmy proces 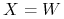 , czyli
, czyli 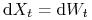 (a więc w równaniu (9.2)
(a więc w równaniu (9.2) 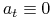 oraz
oraz
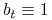 ). Badamy proces
). Badamy proces 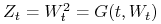 . Na mocy lematu
Itô, proces
. Na mocy lematu
Itô, proces 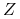 spełnia równanie
spełnia równanie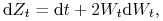
co w postaci całkowej oznacza, że
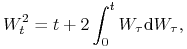
skąd otrzymujemy
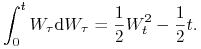
Rozwiązanie równania (9.1) i jego własności
Niech ![]() . Wówczas, na mocy Lematu Itô, proces
. Wówczas, na mocy Lematu Itô, proces
![]() , gdzie
, gdzie ![]() jest dane przez (9.1), spełnia
następujące równanie
jest dane przez (9.1), spełnia
następujące równanie
które po uporządkowaniu przyjmuje następującą postać:
| (9.7) |
W postaci całkowej (9.7) oznacza, że
| (9.8) |
skąd otrzymujemy
| (9.9) |
W ten sposób ,,otrzymaliśmy” rozwiązanie równania stochastycznego
(9.1). Przedstawiona powyżej metoda rozwiązania nie jest w
pełni poprawna, bo po pierwsze zakłada istnienie rozwiązania, a po
drugie zakłada jego dodatniość. O ile istnienie rozwiązania możemy
uzyskać stosunkowo łatwo, powołując się na stosowne twierdzenie o
istnieniu rozwiązań równania typu (9.2), to dodatniość
rozwiązania nie jest taka oczywista. Możemy jednak naprawić nasze
,,rozwiązanie” w następujący sposób. Po prostu wystarczy sprawdzić
czy proces ![]() zdefiniowany równaniem (9.9)
spełnia równanie (9.1) (Zadanie na Ćwiczenia).
zdefiniowany równaniem (9.9)
spełnia równanie (9.1) (Zadanie na Ćwiczenia).
9.2. Rozkład logarytmicznej stopy zwrotu
Z równania (9.10) wynika, że logarytmiczna stopa zwrotu
Stąd wynika, że ,,łatwiej” jest przewidzieć logarytmiczną stopę zwrotu w długim okresie czasu niż w krótszym okresie.
Logarytmiczna stopa oczekiwanego zwrotu
9.3. Zasada wyceny instrumentów pochodnych w modelu ciągłym
Podobnie jak w modelu dyskretnym wycena instrumentów pochodnych polega na przejściu do świata wolnego od ryzyka, w którym aktywa ryzykowne mają taką samą stopę zwrotu jak inwestycje wolne od ryzyka – stopę wolną od ryzyka. To podejście jest oparte na następującym twierdzeniu:
Twierdzenie 9.1
Jeżeli proces ![]() spełnia równanie
spełnia równanie
| (9.13) |
to spełnia również równanie
| (9.14) |
gdzie ![]() jest stopą wolną od ryzyka, a przy przejściu do równania
(9.14) (to jest, przy przejściu do świata wolnego od
ryzyka) dokonaliśmy odpowiedniej zmiany procesu
jest stopą wolną od ryzyka, a przy przejściu do równania
(9.14) (to jest, przy przejściu do świata wolnego od
ryzyka) dokonaliśmy odpowiedniej zmiany procesu ![]() na proces
Wienera
na proces
Wienera ![]() . Ponadto istnieje miara probabilistyczna
. Ponadto istnieje miara probabilistyczna ![]() (tzw. miara martyngałowa) taka, że
(tzw. miara martyngałowa) taka, że
a
sprawiedliwa (wolna od arbitrażu) cena instrumentu pochodnego o
funkcji wypłaty ![]() dana jest wzorem
dana jest wzorem
| (9.15) |
9.4. Wycena instrumentów pochodnych w modelu Blacka-Scholesa
Lemat 9.3
Jeżeli zmienna losowa ![]() ma rozkład log-normalny, to
ma rozkład log-normalny, to
| (9.16) |
gdzie ![]() jest dystrybuantą standardowego rozkładu normalnego,
oraz
jest dystrybuantą standardowego rozkładu normalnego,
oraz
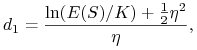 |
(9.17) |
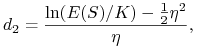 |
(9.18) |
a ![]() jest odchyleniem standardowym zmiennej
jest odchyleniem standardowym zmiennej ![]() .
.
Zapiszmy ![]() w postaci
w postaci
gdzie ![]() jest wartością oczekiwaną zmiennej
jest wartością oczekiwaną zmiennej ![]() ,
, ![]() odchyleniem
standardowym
odchyleniem
standardowym ![]() , a
, a ![]() . Wówczas
. Wówczas
i wtedy
| (9.19) |
gdzie ![]() jest gęstością standardowego
rozkładu normalnego.
jest gęstością standardowego
rozkładu normalnego.
Ponieważ
wyrażenie na wartość oczekiwaną (9.19) zapiszemy w postaci
| (9.20) |
Korzystając z symetrii gęstości standardowego rozkładu normalnego, wyrażenie (9.20) przekształcamy do następującej postaci:
| (9.21) |
gdzie ![]() , a
, a ![]() jest dystrybuantą standardowego
rozkładu normalnego.
jest dystrybuantą standardowego
rozkładu normalnego.
Z własności zmiennych losowych o rozkładzie log-normalnym wynika, że
| (9.22) |
Wykorzystując ten związek pokazujemy, że ![]() i
i ![]() są określone
wyrażeniami (9.17) i (9.18) odpowiednio. Ponadto
są określone
wyrażeniami (9.17) i (9.18) odpowiednio. Ponadto
![]() , co, po uwzględnieniu w (9.21) daje
nam ostatecznie (9.16).
, co, po uwzględnieniu w (9.21) daje
nam ostatecznie (9.16).
9.5. Formuły Blacka-Scholesa dla europejskich opcji waniliowych
![]() Opcje kupna
Opcje kupna
Wycenimy europejską opcję kupna aktywa, które nie przynosi dochodu w
trakcie trwania opcji. Zakładamy, że cena aktywa ![]() spełnia
równanie (9.1). Zgodnie z zasadą wyceny instrumentów
pochodnych wartość opcji kupna dana jest wzorem
spełnia
równanie (9.1). Zgodnie z zasadą wyceny instrumentów
pochodnych wartość opcji kupna dana jest wzorem
gdzie ![]() jest miarą
martyngałową w świecie wolnym od ryzyka. W tym świecie cena aktywa
jest procesem opisanym równaniem
jest miarą
martyngałową w świecie wolnym od ryzyka. W tym świecie cena aktywa
jest procesem opisanym równaniem
| (9.23) |
gdzie ![]() jest stopą zwrotu z inwestycji wolnych od ryzyka (która
pojawia się w miejsce stopy
jest stopą zwrotu z inwestycji wolnych od ryzyka (która
pojawia się w miejsce stopy ![]() w (9.1)), a
w (9.1)), a ![]() jest odpowiednio zmodyfikowanym procesem Wienera, który pojawia się
w miejsce procesu Wienera
jest odpowiednio zmodyfikowanym procesem Wienera, który pojawia się
w miejsce procesu Wienera ![]() w (9.1) przy przejściu do świata
wolnego od ryzyka. Wówczas,
w (9.1) przy przejściu do świata
wolnego od ryzyka. Wówczas, ![]() ma rozkład log-normalny (patrz
(9.10)) oraz jak wynika z (9.11)
ma rozkład log-normalny (patrz
(9.10)) oraz jak wynika z (9.11)
| (9.24) |
Po wstawieniu równości (9.24) do wzoru (9.16) z Lematu 9.3 otrzymujemy
| (9.25) |
gdzie wyrażenia na ![]() i
i ![]() przyjmują postać
przyjmują postać
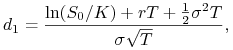 |
(9.26) |
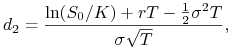 |
(9.27) |
przy przekształceniu których uwzględniliśmy fakt, że odchylenie
standardowe ![]() wynosi
wynosi ![]() (patrz
(9.10)).
(patrz
(9.10)).
![]() Opcje sprzedaży
Opcje sprzedaży
Europejską opcję sprzedaży możemy wycenić stosując podobne podejście jak w przypadku opcji kupna – przez obliczenie wyrażenia
korzystając z odpowiednio zmodyfikowanego Lematu 9.3. Możemy też posłużyć się parytetem opcji kupna-sprzedaży dla wyliczenia wartości opcji sprzedaży z wartości opcji kupna. Postępując w ten drugi sposób otrzymujemy
co, po skorzystaniu z
tożsamości ![]() , zapiszemy w następującej postaci
, zapiszemy w następującej postaci
| (9.28) |
Wzory (9.25) i (9.28) przedstawiają wycenę opcji w
chwili ![]() , których czas trwania wynosił
, których czas trwania wynosił ![]() . Przyjęcie
. Przyjęcie ![]() było
tylko kwestią wygody. Wycenę opcji w chwili
było
tylko kwestią wygody. Wycenę opcji w chwili ![]() uzyskujemy
traktując
uzyskujemy
traktując ![]() jako chwilę początkową, w której znamy wartości
argumentów funkcji
jako chwilę początkową, w której znamy wartości
argumentów funkcji ![]() i
i ![]() , a
, a ![]() jako pozostały do wygaśnięcia
opcji czas trwania. W szczególności, jako wartość początkową aktywa
bierzemy
jako pozostały do wygaśnięcia
opcji czas trwania. W szczególności, jako wartość początkową aktywa
bierzemy ![]() – jego wartość ustaloną w chwili
– jego wartość ustaloną w chwili ![]() . Wówczas
wzory na wycenę opcji waniliowych przyjmują postać
. Wówczas
wzory na wycenę opcji waniliowych przyjmują postać
| (9.29) |
| (9.30) |
gdzie
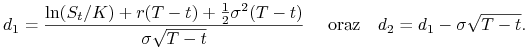 |
(9.31) |
We wzorach (9.29)–(9.31) stopa procentowa ![]() oraz zmienność
oraz zmienność ![]() oznaczają ich wartości ustalone w chwili
wyceny
oznaczają ich wartości ustalone w chwili
wyceny ![]() na pozostały do wygaśnięcia opcji czas trwania, przy czym
dla czytelności zapisu zaznaczenie zależności tych zmiennych od
na pozostały do wygaśnięcia opcji czas trwania, przy czym
dla czytelności zapisu zaznaczenie zależności tych zmiennych od ![]() zostało pominięte.
zostało pominięte.
Uwaga 9.2
Wzory: (9.29) na wartość opcji kupna i (9.30) na
wartość opcji sprzedaży możemy zapisać jedną formułą z dodatkowym
parametrem ![]() , który będzie określał która opcja, kupna czy
sprzedaży, jest wyceniana. Mianowicie formuła
, który będzie określał która opcja, kupna czy
sprzedaży, jest wyceniana. Mianowicie formuła
| (9.32) |
dla ![]() daje wycenę opcji kupna, a dla
daje wycenę opcji kupna, a dla ![]() wycenę
opcji sprzedaży.
wycenę
opcji sprzedaży.
I n t e r p r e t a c j e:
-
Wartość dystrybuanty
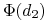 określa prawdopodobieństwo
(w świecie wolnym od ryzyka) wykonania opcji kupna.
określa prawdopodobieństwo
(w świecie wolnym od ryzyka) wykonania opcji kupna. -
Na wzór (9.25) na wycenę opcji kupna możemy spojrzeć jak na wartość portfela, który składa się z
-
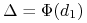 ,,sztuk” aktywa
ryzykownego, oraz
,,sztuk” aktywa
ryzykownego, oraz -
inwestycji w instrument wolny od ryzyka (rachunek bankowy) na kwotę równą
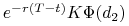 .
.
-
Zbadamy teraz zachowanie się formuł na wycenę w kilku skrajnych przypadkach. Zrobimy to w przypadku opcji kupna.
![]()
![]() (opcja kupna mocno w cenie)
(opcja kupna mocno w cenie)
Wówczas ![]() ,
, ![]() są duże i wtedy
są duże i wtedy ![]() oraz
oraz ![]() są
bliskie jedności. Zatem, w tym przypadku
są
bliskie jedności. Zatem, w tym przypadku
czyli wartość opcji kupna jest w przybliżeniu równa wartości kupionego kontraktu Forward. Możemy powiedzieć, że opcja kupna mocno w cenie jest równoważna kupionemu kontraktowi Forward.
![]()
![]() (opcja kupna mocno poza ceną)
(opcja kupna mocno poza ceną)
Wówczas ![]() oraz
oraz ![]() i wtedy
i wtedy ![]() oraz
oraz
![]() są bliskie zera. Zatem, w tym przypadku
są bliskie zera. Zatem, w tym przypadku
czyli opcja jest prawie bezwartościowa.
![]()
![]()
Niech ![]() oznacza cenę forward w chwili
oznacza cenę forward w chwili ![]() aktywa
dla kontraktu, który zapada w
aktywa
dla kontraktu, który zapada w ![]() .
.
(a) Dla ![]() , czyli gdy
, czyli gdy ![]()
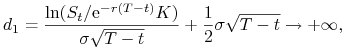 |
oraz
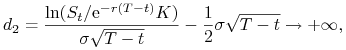 |
przy
![]() . Wówczas
. Wówczas
(b) Dla ![]() , czyli gdy
, czyli gdy ![]()
Zatem
(c) Dla ![]() , czyli gdy
, czyli gdy ![]()
Wówczas
Pokazaliśmy więc, że gdy ![]() , to
, to
![]()
![]() (warunek brzegowy dla
opcji)
(warunek brzegowy dla
opcji)
(a) Dla ![]()
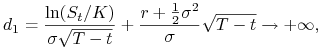 |
oraz
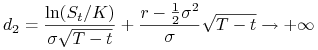 |
przy ![]() . Wówczas
. Wówczas
(b) Dla ![]()
Zatem
(c) Dla ![]()
o ile istnieje granica
![]() , i wtedy
, i wtedy
Pokazaliśmy więc, że spełniony jest warunek brzegowy, w tym sensie, że
9.6. Proste uogólnienia formuł Blacka-Scholesa
![]() Aktywo ryzykowne przynosi ,,dyskretny” dochód
(np. akcja z dywidendą)
Aktywo ryzykowne przynosi ,,dyskretny” dochód
(np. akcja z dywidendą)
Niech ![]() oznacza wartość bieżącą dochodu, który da aktywo w
trakcie pozostałego do wygaśnięcia opcji okresu. Wówczas wartość
opcji dana jest wzorami (9.25) – (9.28), w
których w miejsce
oznacza wartość bieżącą dochodu, który da aktywo w
trakcie pozostałego do wygaśnięcia opcji okresu. Wówczas wartość
opcji dana jest wzorami (9.25) – (9.28), w
których w miejsce ![]() podstawiamy
podstawiamy ![]() . Jeżeli zmienność
. Jeżeli zmienność
![]() jest estymowana na podstawie zaobserwowanych historycznych
wartości aktywa, to zmienność którą należy użyć przy obliczaniu
jest estymowana na podstawie zaobserwowanych historycznych
wartości aktywa, to zmienność którą należy użyć przy obliczaniu
![]() i
i ![]() jest w przybliżeniu tą wyestymowaną zmiennością
historyczną przemnożoną przez współczynnik
jest w przybliżeniu tą wyestymowaną zmiennością
historyczną przemnożoną przez współczynnik ![]() .
Natomiast zmienność implikowana (patrz Wykład 11),
jeśli jest stosowana do wyceny opcji, nie wymaga żadnej korekcji.
.
Natomiast zmienność implikowana (patrz Wykład 11),
jeśli jest stosowana do wyceny opcji, nie wymaga żadnej korekcji.
![]() Aktywo ryzykowne przynosi ,,ciągły” dochód
(np. indeks giełdowy, kurs walutowy)
Aktywo ryzykowne przynosi ,,ciągły” dochód
(np. indeks giełdowy, kurs walutowy)
Zakładamy, że ![]() spełnia (w świecie wolnym od ryzyka) następujące
równanie
spełnia (w świecie wolnym od ryzyka) następujące
równanie
| (9.33) |
gdzie ![]() jest stopą wolną od ryzyka, a
jest stopą wolną od ryzyka, a ![]() jest stopą dochodu
(stopą dywidendy), kapitalizowanymi w sposób ciągły. Korzystając z
Lematu Itô, można łatwo pokazać, że wówczas proces
jest stopą dochodu
(stopą dywidendy), kapitalizowanymi w sposób ciągły. Korzystając z
Lematu Itô, można łatwo pokazać, że wówczas proces
![]() spełnia równanie
spełnia równanie
| (9.34) |
Ponadto, w chwili wygaśnięcia opcji ![]() . Zatem, opcje,
których instrumentem podstawowym jest
. Zatem, opcje,
których instrumentem podstawowym jest ![]() płacące ciągłą dywidendę,
możemy traktować jak opcje których instrumentem podstawowym jest
aktywo
płacące ciągłą dywidendę,
możemy traktować jak opcje których instrumentem podstawowym jest
aktywo ![]() niepłacące dywidendy i wycenić je wzorami
(9.25)–(9.28) dla wartości początkowej aktywa
niepłacące dywidendy i wycenić je wzorami
(9.25)–(9.28) dla wartości początkowej aktywa
![]() . Wzory te przyjmują wówczas następującą
postać
. Wzory te przyjmują wówczas następującą
postać
| (9.35) |
| (9.36) |
gdzie
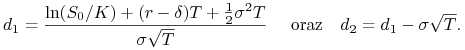 |
(9.37) |
Analogicznie, jak poprzednio wzory na wycenę w dowolnej chwili czasu
![]() mają postać
mają postać
| (9.38) |
| (9.39) |
gdzie
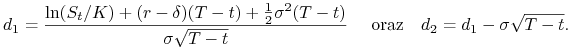 |
(9.40) |
9.7. Wycena instrumentów pochodnych metodą Monte Carlo
Uzyskanie jawnych wzorów analitycznych na wycenę waniliowych opcji
europejskich było możliwe dzięki szczególnej postaci funkcji wypłaty
tych opcji i rozkładu zmiennej ![]() , które umożliwiały obliczenie
wartości oczekiwanej we wzorze na wycenę instrumentu pochodnego
, które umożliwiały obliczenie
wartości oczekiwanej we wzorze na wycenę instrumentu pochodnego
| (9.44) |
W przypadku, gdy obliczenie całki występującej w (9.44)
jest niemożliwe lub trudne do przeprowadzenia, jedynym ze sposobów
na uzyskanie przybliżonej wartości ![]() jest zastosowanie
symulacji Monte Carlo.
jest zastosowanie
symulacji Monte Carlo.
Naiwny algorytm symulacji Monte Carlo dla opcji o europejskim typie wykonania:
-
Dla
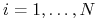
-
Generuj trajektorię
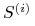 procesu
procesu  w
świecie wolnym od ryzyka startując z wartości początkowej
w
świecie wolnym od ryzyka startując z wartości początkowej 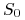 aż
do chwili zapadalności instrumentu pochodnego
aż
do chwili zapadalności instrumentu pochodnego  zgodnie z
przyjętym modelem stochastycznym.
zgodnie z
przyjętym modelem stochastycznym. -
Dla wygenerowanej trajektorii
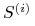 wyznacz wartość wypłaty instrumentu pochodnego
wyznacz wartość wypłaty instrumentu pochodnego
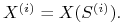
-
-
Oblicz przybliżoną wartość instrumentu pochodnego
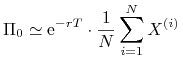
(9.45)
W przypadku gdy ![]() spełnia równanie (9.14), generowanie
trajektorii jest proste, bowiem znamy dokładne rozwiązanie tego
równania – patrz (9.9) z
spełnia równanie (9.14), generowanie
trajektorii jest proste, bowiem znamy dokładne rozwiązanie tego
równania – patrz (9.9) z ![]() . Korzystając z tego
rozwiązania, wartości
. Korzystając z tego
rozwiązania, wartości ![]() w chwilach czasu
w chwilach czasu ![]() generujemy w następujący sposób
generujemy w następujący sposób
| (9.46) |
gdzie ![]() a
a ![]() są niezależnymi zmiennymi losowymi o
rozkładzie normalnym
są niezależnymi zmiennymi losowymi o
rozkładzie normalnym ![]() .
.
Uwagi
-
Jeżeli wypłata instrumentu pochodnego zależy tylko od wartości instrumentu podstawowego w chwili
 i dysponujemy dokładnym rozwiązaniem
równania opisującego proces
i dysponujemy dokładnym rozwiązaniem
równania opisującego proces  , nie musimy symulować wartości
, nie musimy symulować wartości
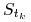 dla
dla 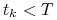 . Możemy od razu generować wartości
. Możemy od razu generować wartości 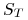 . Na
przykład, gdy
. Na
przykład, gdy  spełnia równanie (9.14),
spełnia równanie (9.14), 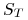 generujemy
korzystając ze wzoru
generujemy
korzystając ze wzoru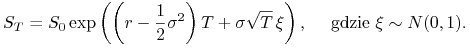
(9.47) -
Jeżeli wypłata instrumentu pochodnego zależy od trajektorii procesu
 (zależy od drogi) – jak np. przypadku opcji
azjatyckich – musimy symulować wartości
(zależy od drogi) – jak np. przypadku opcji
azjatyckich – musimy symulować wartości 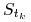 (w chwilach czasu
(w chwilach czasu
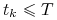 ) od których zależy wartość wypłaty.
) od których zależy wartość wypłaty. -
W przypadku, gdy nie mamy dokładnego rozwiązania równania stochastycznego, które opisuje proces
 , symulując ten proces
musimy się posłużyć zdyskretyzowaną postacią równania
stochastycznego. Na przykład, dla równania (9.2) napisanego
dla procesu
, symulując ten proces
musimy się posłużyć zdyskretyzowaną postacią równania
stochastycznego. Na przykład, dla równania (9.2) napisanego
dla procesu  , wartości
, wartości  symulujemy korzystając z
symulujemy korzystając z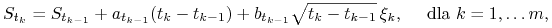
(9.48) gdzie
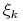 są niezależnymi zmiennymi losowymi
o rozkładzie normalnym
są niezależnymi zmiennymi losowymi
o rozkładzie normalnym 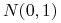 i poruszając się dostatecznie małymi
krokami czasowymi
i poruszając się dostatecznie małymi
krokami czasowymi 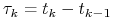 .
.
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 9.2
Pokaż, że jeżeli ![]() , gdzie
, gdzie ![]() , (inaczej
, (inaczej
![]() ), to
), to
oraz
Jeżeli ![]() to
funkcja tworząca momenty
to
funkcja tworząca momenty ![]() dla
dla
![]() .
.
Ćwiczenie 9.3
Niech ![]() , gdzie
, gdzie ![]() spełnia równanie
spełnia równanie
a ![]() ,
, ![]() i
i
![]() są stałymi. Wyprowadź równanie na proces
są stałymi. Wyprowadź równanie na proces ![]() .
.
Ćwiczenie 9.4
Niech ![]() , gdzie
, gdzie ![]() spełnia równanie
spełnia równanie
a ![]() ,
, ![]() i
i ![]() są stałymi. Wyprowadź równanie na proces
są stałymi. Wyprowadź równanie na proces ![]() .
.
Ćwiczenie 9.5
-
(a) Cash-or-Nothing Options
Wyceń europejskie opcje binarne, których wypłaty dane są funkcjami:
-
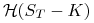 dla opcji kupna,
dla opcji kupna,
oraz
-
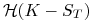 dla opcji sprzedaży,
dla opcji sprzedaży,
gdzie
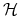 jest funkcją Heaviside'a.
jest funkcją Heaviside'a. -
-
(b) Asset-or-Nothing Options
Wyceń europejskie opcje binarne, których wypłaty dane są funkcjami:
-
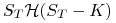 dla opcji kupna,
dla opcji kupna,
oraz
-
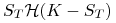 dla opcji
sprzedaży,
dla opcji
sprzedaży,
gdzie
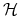 jest funkcją Heaviside'a.
jest funkcją Heaviside'a. -
Jeśli dobrze zrozumiałeś wyprowadzenie wzorów Blacka-Scholesa, to będziesz umiał z nich ,,odczytać” rozwiązanie.
Ćwiczenie 9.6
Wyceń europejską opcję ,,zapłać później”, to jest opcję europejską za którą nabywca płaci premię w chwili wygaśnięcia opcji tylko wtedy gdy opcja wygasa w cenie.
Ćwiczenie 9.7
Wyceń europejską opcję, której ceną wykonania będzie ustalona
wielokrotność zaobserwowanej ceny aktywa w ustalonej chwili czasu
![]() w trakcie trwania opcji. Na przykład, dla opcji kupna wartość
wypłaty tej opcji dana jest wzorem
w trakcie trwania opcji. Na przykład, dla opcji kupna wartość
wypłaty tej opcji dana jest wzorem ![]() ,
gdzie
,
gdzie ![]() , a
, a ![]() jest dane.
jest dane.
Ćwiczenie 9.8
Dla opcji sprzedaży sformułuj i udowodnij lemat analogiczny do Lematu 9.3.
Ćwiczenie 9.9
Rozpatrzmy europejskie opcje azjatyckie o ustalonej cenie wykonania
![]() , których wartość wypłaty zależy od średniej geometrycznej
, których wartość wypłaty zależy od średniej geometrycznej
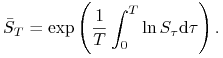 |
Przy założeniu że proces ![]() spełnia równanie (9.1), oblicz
spełnia równanie (9.1), oblicz
-
(a) wariancję
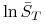 ,
, -
(b) wartość oczekiwaną
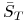 ,
, -
(c) cenę azjatyckiej opcji kupna.
Ćwiczenie 9.10
Rozpatrzmy opcje europejskie o czasie trwania ![]() , które są w chwili
bieżącej at-the-money forward, to znaczy takie, których
cena wykonania
, które są w chwili
bieżącej at-the-money forward, to znaczy takie, których
cena wykonania ![]() i bieżąca cena akcji
i bieżąca cena akcji ![]() spełniają warunek
spełniają warunek
gdzie ![]() jest stopą wolną od ryzyka, a
jest stopą wolną od ryzyka, a
![]() stopą (ciągłej) dywidendy.
stopą (ciągłej) dywidendy.
Pokaż, że w tym przypadku ceny opcji call i put są takie same i wynoszą
Ponadto, pokaż, że dla małych wartości ![]() , zachodzi
przybliżony wzór
, zachodzi
przybliżony wzór
W
powyższych wzorach ![]() oznacza zmienność akcji, a
oznacza zmienność akcji, a ![]() –
dystrybuantę rozkładu
–
dystrybuantę rozkładu ![]() .
.