Zagadnienia
- 2.1 Podstawowe stopy procentowe
- 2.2 Obligacje zerokuponowe, czynniki dyskontowe
- 2.3 Wartość strumienia przepływów pieniężnych
- 2.4 Zerokuponowe stopy procentowe (spotowe, natychmiastowe)
- 2.5 Struktura stóp procentowych
- 2.6 Chwilowa stopa natychmiastowa
- 2.7 Stopy forward
- 2.8 Chwilowa stopa forward
- Zagadnienia i zadania na Ćwiczenia
2. Stopy procentowe
2.1. Podstawowe stopy procentowe
Na rynku obserwujemy wiele różnych stóp procentowych, z których każda na swój sposób określa cenę pieniądza w czasie i ewentualnie premię za ryzyko kredytowe:
-
stopy skarbowe – stopy po których rządy państw pożyczają pieniądze w swoim kraju – rentowności bonów skarbowych (w przypadku amerykańskich bonów skarbowych (T-bills) stopa dyskonta), stopy dochodowości obligacji skarbowych (T-bonds),
-
stopy repo – stopy transakcji repo (ang. repurchase agreement), to jest transakcji, która polega na sprzedaży papieru wartościowego z przyrzeczeniem odkupu (różnica między ceną odkupu a ceną sprzedaży to odsetki),
-
stopy międzybankowe – stopy lokat i depozytów na rynku międzybankowym – w tym stopy referencyjne typu LIBOR, WIBOR, EURIBOR.
Dla transakcji o takim samym czasie trwania mamy następującą nierówność
przy założeniu, że stopy te zostały sprowadzone do tej samej ,,bazy” (są wyrażone w tej samej konwencji – o tym będzie mowa później). Nierówność powyższa wynika z różnych poziomów ryzyka kredytowego, zawartego w transakcjach którym te stopy odpowiadają.
Prócz tych stóp mamy jeszcze na rynku międzybankowym
-
stopy swapowe – stopy kontraktów wymiany procentowej IRS,
-
stopy FRA – to są de facto stopy forward.
Wyżej wymienione stopy są bezpośrednio obserwowane na rynku, to znaczy są kwotowane lub są ogłaszane. Jest też grupa instrumentów finansowych, których (kwotowane) ceny implikują odpowiedniego rodzaju stopy procentowe. Na przykład mamy
-
stopy dochodowości obligacji skarbowych, papierów komercyjnych (bonów, obligacji emitowanych przez podmioty gospodarcze) (ang. yield to maturity, internal rate of return),
-
stopy forward implikowane przez kontrakty futures na depozyty (Eurodollar futures).
W matematyce finansowej i w inżynierii finansowej używa się również wielu stóp teoretycznych, które nie są obserwowalne na rynku.
Mówiąc o stopie procentowej na ogół odnosimy ją do okresu czasu, w którym ,,żyje” instrument finansowy związany z tą stopą. Oznaczenia dla czasu będziemy często stosować w podwójnych znaczeniach:
-
raz zmienne czasowe, np.
 ,
,  , będą oznaczać daty (dni),
, będą oznaczać daty (dni), -
innym razem
 ,
,  będą punktami (liczbami rzeczywistymi)
na osi czasu, które odpowiadają odległości chwil
będą punktami (liczbami rzeczywistymi)
na osi czasu, które odpowiadają odległości chwil  ,
,  od pewnego
ustalonego dnia (początku osi czasu), przy czym odległości te będą
liczone według pewnego sposobu (konwencji).
od pewnego
ustalonego dnia (początku osi czasu), przy czym odległości te będą
liczone według pewnego sposobu (konwencji).
Zwykle będziemy przyjmować, że bieżący dzień jest początkiem osi czasu.
Odległość między dwoma chwilami czasu mierzymy w latach, bowiem
stopy procentowe będziemy zawsze podawać zannualizowane,
tzn. w skali roku (rok jest jednostką czasu). Należy jeszcze zwrócić
uwagę na sprecyzowanie co to znaczy ,,rok”. I tak, odległość między
![]() a
a ![]() , którą będziemy oznaczać symbolem
, którą będziemy oznaczać symbolem ![]() , może być
zdefiniowana
, może być
zdefiniowana
-
w konwencji ACT/365 jako
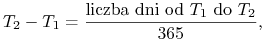
-
w konwencji ACT/360 jako
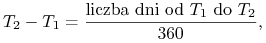
-
w konwencji 30/360 jako
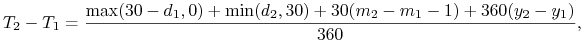
gdzie
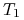 potraktowane jako data zapisaliśmy w postaci
potraktowane jako data zapisaliśmy w postaci
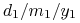 , i analogicznie
, i analogicznie 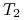 w postaci
w postaci 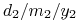 – w
tej konwencji liczba dni między dwoma dniami jest liczona przy
założeniu, że każdy miesiąc ma 30 dni.
– w
tej konwencji liczba dni między dwoma dniami jest liczona przy
założeniu, że każdy miesiąc ma 30 dni.
Przyjmijmy następujące oznaczenia
-
 – chwila czasu (dzień), w której instrument finansowy (stopa z nim
związana) jest ,,obserwowany”,
– chwila czasu (dzień), w której instrument finansowy (stopa z nim
związana) jest ,,obserwowany”, -
 – data zapadalności instrumentu (stopy),
– data zapadalności instrumentu (stopy), -
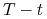 – czas trwania (czas do zapadalności).
– czas trwania (czas do zapadalności).
2.2. Obligacje zerokuponowe, czynniki dyskontowe
Obligacja zerokuponowa o terminie zapadalności ![]() to
instrument finansowy, który gwarantuje posiadaczowi wypłatę w
wysokości 1 (w danej walucie) w chwili czasu
to
instrument finansowy, który gwarantuje posiadaczowi wypłatę w
wysokości 1 (w danej walucie) w chwili czasu ![]() . Niech
. Niech
oznacza wartość tego instrumentu w chwili ![]() , gdzie
, gdzie ![]() .
.
Tak zdefiniowane obligacje zerokuponowe są teoretycznym instrumentem finansowym i w rzeczywistości występują na rynku rzadko. Na przykład, bony skarbowe są obligacjami zerokuponowymi i w danej chwili na rynku jest tylko skończona liczba tych bonów o czasach trwania, które nie przekraczają roku. Obligacje zerokuponowe są fundamentalnym pojęciem używanym w teorii stóp procentowych, które pozwala powiązać lub wyznaczyć większość stóp procentowych: te występujące na rynku, oraz stopy teoretyczne, nieobserwowalne na rynku.
Własności ![]()
-
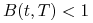 dla
dla 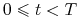 ,
, -
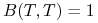 ,
, -
obserwując w chwili
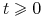 :
:-
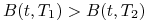 dla każdych
dla każdych 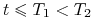 , tj. funkcja
, tj. funkcja 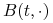 jest malejąca,
jest malejąca, -
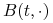 jest
różniczkowalna (to jest założenie),
jest
różniczkowalna (to jest założenie),
-
-
dla każdego
 :
: 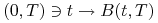 jest
procesem stochastycznym.
jest
procesem stochastycznym.
Czynniki dyskontowe
Czynnik dyskontowy, który sprowadza do chwili ![]() wartość przepływu
pieniężnego następującego w
wartość przepływu
pieniężnego następującego w ![]() , będziemy oznaczać symbolem
, będziemy oznaczać symbolem
![]() . Wartość (cena) w chwili
. Wartość (cena) w chwili ![]() obligacji zero-kuponowej o
terminie zapadalności
obligacji zero-kuponowej o
terminie zapadalności ![]() może być używana do dyskontowania na
chwilę
może być używana do dyskontowania na
chwilę ![]() wartości przepływu pieniężnego następującego w chwili
wartości przepływu pieniężnego następującego w chwili
![]() . Zatem, w szczególności, jeżeli istnieje obligacja zerokuponowa
zapadalna w
. Zatem, w szczególności, jeżeli istnieje obligacja zerokuponowa
zapadalna w ![]() , to
, to ![]() i wówczas te dwa pojęcia
możemy używać wymiennie. By zaznaczyć walutę (CUR) w której
dyskontowany jest przepływ pieniężny będziemy czasami stosować
notację
i wówczas te dwa pojęcia
możemy używać wymiennie. By zaznaczyć walutę (CUR) w której
dyskontowany jest przepływ pieniężny będziemy czasami stosować
notację ![]() . Wartości czynników dyskontowych
można wyznaczyć również na podstawie kwotowań innych instrumentów
finansowych, na przykład na podstawie stóp depozytowych, stóp
kontraktów FRA oraz stóp kontraktów IRS (patrz Wykłady 3 i 4).
. Wartości czynników dyskontowych
można wyznaczyć również na podstawie kwotowań innych instrumentów
finansowych, na przykład na podstawie stóp depozytowych, stóp
kontraktów FRA oraz stóp kontraktów IRS (patrz Wykłady 3 i 4).
Uwaga 2.1
W teorii modeli stóp procentowych definiuje się również stochastyczny czynnik dyskontowy
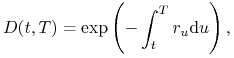 |
gdzie ![]() jest
krótkoterminową (chwilową) stopą natychmiastową (o tej stopie
będziemy mówić w dalszej części wykładu). W ramach tej teorii
pokazuje się, że
jest
krótkoterminową (chwilową) stopą natychmiastową (o tej stopie
będziemy mówić w dalszej części wykładu). W ramach tej teorii
pokazuje się, że
gdzie ![]() jest tzw. filtracją (zasobem informacji
dostępnej do chwili
jest tzw. filtracją (zasobem informacji
dostępnej do chwili ![]() włącznie).
włącznie).
2.3. Wartość strumienia przepływów pieniężnych
Niech ![]() oznacza przepływ pieniężny, który następuje w chwili
oznacza przepływ pieniężny, który następuje w chwili
![]() . Wartość strumienia (portfela) przepływów
. Wartość strumienia (portfela) przepływów
![]() (następujących w tej samej walucie) w
chwili
(następujących w tej samej walucie) w
chwili ![]() wynosi
wynosi
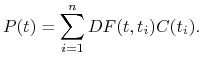 |
(2.1) |
Jeśli ![]() (chwila bieżąca),
(chwila bieżąca), ![]() nazywamy wartością bieżącą
strumienia
nazywamy wartością bieżącą
strumienia ![]() . Ponieważ wiele instrumentów
finansowych można przedstawić w postaci strumienia przepływów
pieniężnych, wzór (2.1) jest podstawowym modelem wyceny
takich instrumentów. Nawet jeśli instrumenty tego typu mają cenę
rynkową i formalnie nie ma potrzeby dokonywania wyceny na podstawie
modelu (wzorem (2.1)), model wyceny jest niezbędny od
wyznaczania miar ryzyka takiego instrumentu – na przykład duracji
(inaczej: średniego czasu trwania), czy też BPV (ang. Basis
Point Value) – patrz Zadanie 2.8.
. Ponieważ wiele instrumentów
finansowych można przedstawić w postaci strumienia przepływów
pieniężnych, wzór (2.1) jest podstawowym modelem wyceny
takich instrumentów. Nawet jeśli instrumenty tego typu mają cenę
rynkową i formalnie nie ma potrzeby dokonywania wyceny na podstawie
modelu (wzorem (2.1)), model wyceny jest niezbędny od
wyznaczania miar ryzyka takiego instrumentu – na przykład duracji
(inaczej: średniego czasu trwania), czy też BPV (ang. Basis
Point Value) – patrz Zadanie 2.8.
2.4. Zerokuponowe stopy procentowe (spotowe, natychmiastowe)
Zerokuponowa stopa prosta dla okresu ![]() to wewnętrzna
stopa zwrotu obligacji zerokuponowej zapadalnej w chwili
to wewnętrzna
stopa zwrotu obligacji zerokuponowej zapadalnej w chwili ![]() wyznaczona jako stopa o tzw. prostej kapitalizacji odsetek
wyznaczona jako stopa o tzw. prostej kapitalizacji odsetek
| (2.2) |
skąd
| (2.3) |
Wzór (2.2) jest tożsamy z warunkiem
| (2.4) |
który można zinterpretować jako założenie braku arbitrażu. Lewa
strona (2.4) jest kumulacją kapitału (kapitałem wraz z
odsetkami) złożonego na lokacie, której oprocentowanie wynosi
![]() , na okres od
, na okres od ![]() do
do ![]() . Prawa strona jest wypłatą w chwili
. Prawa strona jest wypłatą w chwili
![]() z inwestycji polegającej na zakupie w chwili
z inwestycji polegającej na zakupie w chwili ![]()
![]() jednostek zerokuponowej obligacji, która zapada w
jednostek zerokuponowej obligacji, która zapada w ![]() . By nie było
arbitrażu, obie te inwestycje muszą dać ten sam dochód. Stąd musi
zachodzić (2.4).
. By nie było
arbitrażu, obie te inwestycje muszą dać ten sam dochód. Stąd musi
zachodzić (2.4).
Zerokuponowa stopa kapitalizowana w sposób ciągły dla
okresu ![]() to wewnętrzna stopa zwrotu obligacji zerokuponowej
zapadalnej w chwili
to wewnętrzna stopa zwrotu obligacji zerokuponowej
zapadalnej w chwili ![]() wyznaczona jako stopa o tzw. ciągłej
kapitalizacji odsetek
wyznaczona jako stopa o tzw. ciągłej
kapitalizacji odsetek
| (2.5) |
skąd
| (2.6) |
Wzór (2.5) jest tożsamy z warunkiem
| (2.7) |
który znów można zinterpretować jako założenie braku arbitrażu, przy czym tym razem kumulacja kapitału jest wyrażona przez stopę kapitalizowaną w sposób ciągły.
Zerokuponowa stopa kapitalizowana ![]() -krotnie w ciągu roku
dla okresu
-krotnie w ciągu roku
dla okresu ![]() to wewnętrzna stopa zwrotu obligacji
zerokuponowej zapadalnej w chwili
to wewnętrzna stopa zwrotu obligacji
zerokuponowej zapadalnej w chwili ![]() wyznaczona jako stopa o tzw.
wyznaczona jako stopa o tzw.
![]() -krotnej (w ciągu roku) kapitalizacji odsetek
-krotnej (w ciągu roku) kapitalizacji odsetek
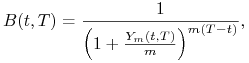 |
(2.8) |
skąd
| (2.9) |
Wzór (2.8) jest tożsamy z warunkiem
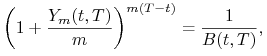 |
(2.10) |
który znów można zinterpretować jako założenie braku arbitrażu, przy
czym kumulacja kapitału jest wyrażona przez stopę kapitalizowaną
![]() -krotnie w ciągu roku.
-krotnie w ciągu roku.
Korzystając z definicji (2.2), (2.5), oraz
(2.8) możemy wyprowadzić formuły wiążące wzajemnie stopy
![]() ,
, ![]() , oraz
, oraz ![]() . Wszystkie te stopy wyrażają to
samo, tj. koszt pieniądza w czasie, z tym że każda na swój sposób.
. Wszystkie te stopy wyrażają to
samo, tj. koszt pieniądza w czasie, z tym że każda na swój sposób.
Określenie stopy ![]() jako stopa kapitalizowanej w sposób ciągły
jest uzasadnione przez następujący fakt (Zadanie na Ćwiczenia).
Mianowicie, jeśli granica
jako stopa kapitalizowanej w sposób ciągły
jest uzasadnione przez następujący fakt (Zadanie na Ćwiczenia).
Mianowicie, jeśli granica ![]() istnieje, to
istnieje, to
Odnosząc się do stopy procentowej, należy jeszcze zwrócić uwagę na
to w jaki sposób obliczana jest długość okresu czasu (wielkość
![]() ). Stopom procentowym o tym samym schemacie kapitalizacji
odsetek można (i tak bywa dla różnych walut) przypisać różne
konwencje, według których obliczana jest długość okresu czasu
). Stopom procentowym o tym samym schemacie kapitalizacji
odsetek można (i tak bywa dla różnych walut) przypisać różne
konwencje, według których obliczana jest długość okresu czasu ![]() .
.
Które z tych stóp widać na rynku ?
-
Stopy proste
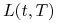 są bezpośrednio obserwowalne na rynku – stopy
lokat / depozytów na rynku międzybankowym.
są bezpośrednio obserwowalne na rynku – stopy
lokat / depozytów na rynku międzybankowym. -
Stopy
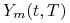 są czasem widoczne jako stopy implikowane –
na przykład, jako stopy dochodowości obligacji zerokuponowych. Dla
obligacji amerykańskich standardem jest stopa kapitalizowana co pół
roku, tj. dla
są czasem widoczne jako stopy implikowane –
na przykład, jako stopy dochodowości obligacji zerokuponowych. Dla
obligacji amerykańskich standardem jest stopa kapitalizowana co pół
roku, tj. dla 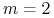 .
. -
Stopy
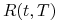 kapitalizowane w sposób ciągły nie są bezpośrednio
widoczne na rynku. Są one natomiast bardzo użyteczne w matematyce
finansowej.
kapitalizowane w sposób ciągły nie są bezpośrednio
widoczne na rynku. Są one natomiast bardzo użyteczne w matematyce
finansowej.
2.5. Struktura stóp procentowych
Struktura stóp procentowych to nic innego jak funkcja
gdzie ![]() oznacza jedną
ze stóp
oznacza jedną
ze stóp ![]() ,
, ![]() ,
, ![]() . Wykres tej funkcji nazywamy
krzywą stóp procentowych.
. Wykres tej funkcji nazywamy
krzywą stóp procentowych.
Bywa, że określając strukturę stóp procentowych używa się dwóch rodzajów stóp, na przykład
Często mówiąc o strukturze stóp procentowych, mamy na myśli de facto strukturę czynników dyskontowych, to jest funkcję
Aspekty praktyczne
-
Mamy dwa podstawowe typy struktur czynników dyskontowych
-
krzywą obligacyjną (,,bondową”), ang. government curve
 wygenerowaną z cen obligacji (skarbowych),
wygenerowaną z cen obligacji (skarbowych), -
krzywą międzybankową (,,swapową”), ang. swap (intermarket) curve
 wygenerowaną na podstawie stóp na rynku
międzybankowym (stóp typu LIBOR, stóp FRA, stóp IRS, cen kontraktów
Futures na depozyty – patrz Wykłady 3 i 4).
wygenerowaną na podstawie stóp na rynku
międzybankowym (stóp typu LIBOR, stóp FRA, stóp IRS, cen kontraktów
Futures na depozyty – patrz Wykłady 3 i 4).
-
-
Krzywa swapowa jest określona przez
-
wartości czynników dyskontowych
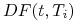 dla chwil czasu
dla chwil czasu 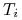 (
(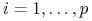 ), które
odpowiadają czasom trwania instrumentów użytych do ich
wygenerowania,
), które
odpowiadają czasom trwania instrumentów użytych do ich
wygenerowania, -
metody interpolacji i ekstrapolacji, przy pomocy których wyznacza się wartości
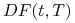 dla
dla  leżących pomiędzy punktami węzłowymi
leżących pomiędzy punktami węzłowymi
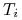 ; na przykład dla
; na przykład dla 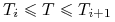 (interpolacja)
określamy
(interpolacja)
określamy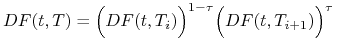
(2.11) 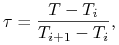
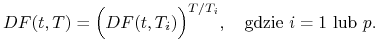
Uwaga: Nie jest to jedyny możliwy sposób interpolacji czynników dyskontowych (patrz Zadanie 2.5). Ten sposób interpolacji ma pewne zalety (patrz Zadanie 2.3.(a) oraz Zadanie 2.4) ale ma też i wady (Zadanie 2.3.(b)).
-
2.6. Chwilowa stopa natychmiastowa
W matematycznym modelowaniu stóp procentowych operuje się również pewnymi abstrakcyjnymi stopami procentowymi. Jedną z takich stóp jest krótkoterminowa (chwilowa) stopa natychmiastowa (ang. spot short interest rate), zdefiniowana w następujący sposób
Dla oznaczenia tej stopy
będziemy również używać symbolu ![]() .
.
Z powyższej definicji, oraz z własności funkcji ![]() wynika,
że
wynika,
że
Można również pokazać (Zadanie na Ćwiczenia), że
Z tego powodu za rynkowy odpowiednik stopy chwilowej czasami przyjmuje się krótkoterminową stopę lokat / depozytów na rynku międzybankowym. Ze względu na czas trwania najbardziej odpowiednią stopą byłaby stopa ON (ang. OverNight). Jednakże, na wielu rynkach, w tym i na polskim, stopa ON ma zbyt dużą zmienność w stosunku do innych stóp rynkowych i nie jest dostatecznie skorelowana z tymi stopami rynkowymi, by mogła ,,tłumaczyć” ich zachowanie. Czasami za surogat stopy chwilowej bierze się trzymiesięczną stopę typu LIBOR.
Dynamikę struktury stóp procentowych próbuje się modelować
formułując stochastyczne równania różniczkowe dla odpowiednio
dobranych stóp procentowych. Podstawowa klasa modeli stóp
procentowych dotyczy stopy chwilowej ![]() . Jednym z takich
modeli jest następujący model Hull-White'a
. Jednym z takich
modeli jest następujący model Hull-White'a
gdzie
-
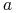 i
i 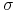 są stałymi,
są stałymi, -
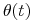 pewną funkcją deterministyczną.
pewną funkcją deterministyczną.
Model Hull-White'a jest modelem z powrotem do średniej – stopa
krótkoterminowa powraca do średniej ![]() w tempie
w tempie ![]() .
Parametry modelu (funkcję
.
Parametry modelu (funkcję ![]() , stałe
, stałe ![]() i
i ![]() ) dobiera
się w taki sposób by dopasować go bieżącej struktury stóp
procentowych.
) dobiera
się w taki sposób by dopasować go bieżącej struktury stóp
procentowych.
2.7. Stopy forward
Określenie stopy forward przy użyciu (prostych) stóp depozytowych
Dla uproszczenia załóżmy, że rozpatrujemy okresy do ![]() (wtedy
możemy stosować konwencje rynku pieniężnego, to jest stopy proste).
(wtedy
możemy stosować konwencje rynku pieniężnego, to jest stopy proste).
Stopa forward obserwowana w chwili ![]() na okres czasu od
na okres czasu od ![]() do
do ![]() ,
gdzie
,
gdzie ![]() , to stopa
, to stopa ![]() w okresie od
w okresie od ![]() do
do ![]() przy
której następujące dwie transakcje dają taki sam wynik w chwili
przy
której następujące dwie transakcje dają taki sam wynik w chwili ![]() :
:
-
Transakcja 1 – w chwili
 lokujemy jednostkę pieniężną na okres
lokujemy jednostkę pieniężną na okres ![[t,S]](wyklady/ifi/mi/mi279.png) po stopie
po stopie 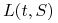
-
Transakcja 2 – w chwili
 lokujemy jednostkę pieniężną na okres
lokujemy jednostkę pieniężną na okres ![[t,T]](wyklady/ifi/mi/mi188.png) po stopie
po stopie 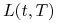 oraz jednocześnie zawieramy umowę na ulokowanie kwoty
oraz jednocześnie zawieramy umowę na ulokowanie kwoty
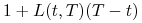 na okres czasu
na okres czasu ![[T,S]](wyklady/ifi/mi/mi127.png) po stopie
po stopie 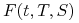
Te dwie transakcje dają ten sam wynik jeśli
| (2.12) |
skąd otrzymamy następujący wzór na stopę forward
| (2.13) |
Stopa forward zdefiniowana (z pozoru) inaczej
Stopa forward obserwowana w chwili ![]() na okres czasu od
na okres czasu od ![]() do
do ![]() (
(![]() ) to stopa zwrotu którą można zrealizować w okresie od
) to stopa zwrotu którą można zrealizować w okresie od ![]() do
do ![]() na transakcji wolnej od ryzyka zawartej w
na transakcji wolnej od ryzyka zawartej w ![]() bez
początkowych kosztów. Taką transakcję przeprowadzamy w następujący
sposób:
bez
początkowych kosztów. Taką transakcję przeprowadzamy w następujący
sposób:
-
w chwili
 sprzedajemy jedną obligację zerokuponową o terminie zapadalności
sprzedajemy jedną obligację zerokuponową o terminie zapadalności
 - otrzymujemy sumę
- otrzymujemy sumę 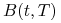 , i jednocześnie,
, i jednocześnie, -
w chwili
 kupujemy obligację zero-kuponową o terminie zapadalności
kupujemy obligację zero-kuponową o terminie zapadalności
 o nominale
o nominale 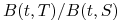 – płacimy sumę
– płacimy sumę 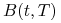 .
.
Następnie,
-
w chwili
 realizujemy zobowiązanie z tytułu sprzedanej obligacji
zerokuponowej o terminie zapadalności
realizujemy zobowiązanie z tytułu sprzedanej obligacji
zerokuponowej o terminie zapadalności  – płacimy 1,
– płacimy 1,
-
w chwili
 otrzymujemy wypłatę z obligacji zerokuponowej o terminie zapadalności
otrzymujemy wypłatę z obligacji zerokuponowej o terminie zapadalności
 – otrzymujemy sumę
– otrzymujemy sumę 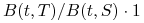 .
.
Zatem w okresie od ![]() do
do ![]() zrealizujemy wolny od ryzyka zwrot w
wysokości
zrealizujemy wolny od ryzyka zwrot w
wysokości
Z tym zwrotem możemy związać następujące stopy:
-
Prostą stopę forward
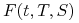 ustaloną w chwili
ustaloną w chwili  na okres
czasu
na okres
czasu ![[T,S]](wyklady/ifi/mi/mi127.png) , która jest określona przez następujący warunek
, która jest określona przez następujący warunek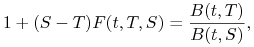
skąd mamy następującą definicję
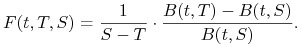
(2.14) -
Stopę forward kapitalizowaną w sposób ciągły
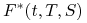 ustaloną w chwili
ustaloną w chwili  na okres czasu
na okres czasu ![[T,S]](wyklady/ifi/mi/mi127.png) , określoną w
następujący sposób
, określoną w
następujący sposób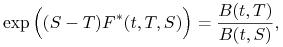
skąd mamy następującą definicję
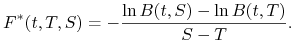
(2.15)
Korzystając z definicji (2.15) można łatwo pokazać, że
| (2.16) |
Z tego wzoru wynika następująca obserwacja:
-
jeśli w okresie czasu
![[T,S]](wyklady/ifi/mi/mi127.png) krzywa stóp procentowych
krzywa stóp procentowych 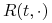 jest
rosnąca (malejąca), to
jest
rosnąca (malejąca), to 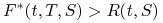 (
(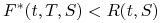 ).
).
Które ze stóp forward widać na rynku?
Proste stopy forward – jako kwotowania kontraktów FRA (patrz Wykład 3) oraz jako stopy implikowane z kwotowań kontraktów Futures na depozyty (patrz Wykład 5).
2.8. Chwilowa stopa forward
Chwilowa stopa forward obserwowana w chwili ![]() o terminie
zapadalności
o terminie
zapadalności ![]() jest zdefiniowana jako następująca granica
jest zdefiniowana jako następująca granica
| (2.17) |
gdzie stopa ![]() jest określona przez warunek (2.14).
Korzystając z (2.14) obliczamy
jest określona przez warunek (2.14).
Korzystając z (2.14) obliczamy
| (2.18) |
Analogicznie pokazujemy, że
Ponadto, jeżeli założymy, że funkcja
![]() jest różniczkowalna, to przechodząc w równaniu
(2.16) do granicy
jest różniczkowalna, to przechodząc w równaniu
(2.16) do granicy ![]() (lub podstawiając w
(2.18) wzór (2.6) i wykonując różniczkowanie),
otrzymamy następujący związek między stopą chwilową forward
(lub podstawiając w
(2.18) wzór (2.6) i wykonując różniczkowanie),
otrzymamy następujący związek między stopą chwilową forward ![]() a stopami natychmiastowymi kapitalizowanymi w sposób ciągły:
a stopami natychmiastowymi kapitalizowanymi w sposób ciągły:
Całkując (2.18) otrzymujemy następujący związek
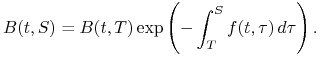 |
(2.19) |
W szczególności
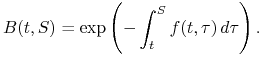 |
(2.20) |
Z (2.20) napisanego dla ![]() i z definicji (2.5)
stopy
i z definicji (2.5)
stopy ![]() wynika następujący związek
wynika następujący związek
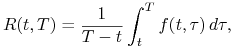 |
(2.21) |
Czyli stopa ![]() jest średnią chwilowych stóp forward w okresie
czasu
jest średnią chwilowych stóp forward w okresie
czasu ![]() . Na koniec zauważmy, że
. Na koniec zauważmy, że
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 2.1
Na rynku kwotowane są następujące stopy (proste, ACT/365)
-
(i) spot L(3M)=5.00%,
-
(ii) forward F(3M,6M)=5.10%, F(3M,9M)=5.15%, F(6M,1Y)=5.20%.
Oblicz
-
(a) stopy spot L(6M), L(9M), L(1Y),
-
(b) stopy forward F(6M,9M), F(9M,1Y),
-
(c) czynniki dyskontowe
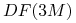 ,
, 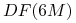 ,
, 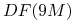 ,
, 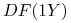 .
.
Załóż, że okres 3M ma 91 dni (od daty spot), 6M 183 dni, 9M 273 dni, oraz 1Y 365 dni.
Ćwiczenie 2.2
Pokazać, że jeśli granica
![]() istnieje, to
istnieje, to
![]()
Ćwiczenie 2.3
(a) Sprawdzić, że jeżeli ciąg ![]() (
(![]() )
jest malejący, to funkcja
)
jest malejący, to funkcja ![]() określona
formułami (2.11) jest malejąca.
określona
formułami (2.11) jest malejąca.
(b) Pokazać, że stopy forward kapitalizowane w sposób ciągły dla
każdego okresu czasu ![]() zawartego w
zawartego w ![]() są
takie same.
są
takie same.
Ćwiczenie 2.4
Wyprowadzić wzory na interpolację i
ekstrapolację stóp ![]() , które odpowiadają interpolacji i
ekstrapolacji czynników dyskontowych określonym formułami
(2.11). Pokazać że, przy tej metodzie interpolacji i
ekstrapolacji stóp
, które odpowiadają interpolacji i
ekstrapolacji czynników dyskontowych określonym formułami
(2.11). Pokazać że, przy tej metodzie interpolacji i
ekstrapolacji stóp ![]() , przesunięciu równoległemu
stóp
, przesunięciu równoległemu
stóp ![]() (
(![]() ) odpowiada równoległe przesunięcie
krzywej
) odpowiada równoległe przesunięcie
krzywej ![]() . Jak zmienia się struktura czynników
dyskontowych przy przesunięciu równoległym stóp procentowych?
. Jak zmienia się struktura czynników
dyskontowych przy przesunięciu równoległym stóp procentowych?
Ćwiczenie 2.5
Wyprowadzić wzory na interpolację czynników dyskontowych
analogiczne do (2.11a), które odpowiadają liniowej
interpolacji stóp ![]() , to jest
, to jest
dla ![]() . Przedyskutować problem monotoniczności
tak zdefiniowanej krzywej czynników dyskontowych
. Przedyskutować problem monotoniczności
tak zdefiniowanej krzywej czynników dyskontowych ![]() względem zmiennej
względem zmiennej ![]() .
.
![]() i
i ![]() , oraz
, oraz ![]() i
i ![]() .
Sprawdź czy dla
.
Sprawdź czy dla ![]() zachodzi
zachodzi ![]() .
.
Ćwiczenie 2.6
Załóżmy, że krzywa zerokuponowych stóp (kapitalizowanych w sposób ciągły) jest rosnąca. Co jest większe
-
stopa zerokuponowa dla terminu
 ,
,
-
wewnętrzna stopa zwrotu z obligacji stałokuponowej o terminie wykupu
 ?
?
Co można powiedzieć, jeśli krzywa stóp procentowych jest malejąca lub stała?
Ćwiczenie 2.7
Na rynku kwotowane są następujące papiery skarbowe
-
(i) sześciomiesięczny bon – po 97,
-
(ii) obligacja kuponowa o kuponie 5.00% płatnym co pół roku zapadająca za rok – po cenie 99,
-
(iii) obligacja kuponowa o kuponie 5.50% płatnym co rok zapadająca za rok i sześć miesięcy – po cenie (czystej) 96.75,
-
(iv) obligacja kuponowa o kuponie 6% płatnym raz w roku zapadająca za dwa lata – po cenie 98.
Oblicz
-
(a) czynniki dyskontowe
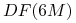 ,
, 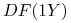 ,
, 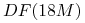 ,
, 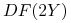 ,
, -
(b) stopy R(6M), R(1Y), R(18M), R(2Y),
-
(c) stopy forward
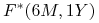 ,
, 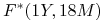 ,
, 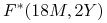 (kapitalizowane w sposób ciągły).
(kapitalizowane w sposób ciągły).
W celu uproszczenia obliczeń przyjmij, że ułamek roku dla każdego
okresu sześciomiesięcznego wynosi ![]() .
.
Ćwiczenie 2.8
Rozwiąż Zadanie 2.7 mając dane tylko (i), (iii) oraz (iv).
Brakujące dane będziesz musiał zastąpić założeniem co do postaci czynnika dyskontowego dla okresu 1Y.
Ćwiczenie 2.9
Dane są dwie obligacje, których czas trwania jest taki sam i
wynosi 5 lat (obligacje zapadają za 5 lat od chwili bieżącej). Obie
obligacje płacą kupon w dokładnie tych samych terminach, ale w
różnych wysokościach. Jedna z nich płaci kupon 7.5% i jej cena
bieżąca wynosi 95. Druga, o 5% kuponie, kosztuje 92.50. Oblicz
wartość czynnika dyskontowego dla okresu 5Y oraz zero-kuponową stopę
procentową ![]() (kapitalizowaną półrocznie) w konwencji
ACT/360.
(kapitalizowaną półrocznie) w konwencji
ACT/360.
Ćwiczenie 2.10
Na rynku są w obrocie dwie obligacje zerokuponowe
-
(i) skarbowa w cenie 98,
-
(ii) korporacyjna (emitowana przez korporację) w cenie 95,
obie zapadające w ciągu 91 dni. Oblicz
-
(a) wewnętrzne stopy zwrotu tych obligacji.
-
(b) spread kredytowy papieru komercyjnego, to jest różnicę między wewnętrzną stopą zwrotu papieru komercyjnego a stopą papieru skarbowego (wolnego od ryzyka kredytowego).
Ćwiczenie 2.11
Wewnętrzna stopa zwrotu dwuletniej obligacji, która płaci 6% kupon co pół roku, wynosi 8% (kapitalizacja półroczna, 30/360).
-
(a) Oblicz cenę tej obligacji.
-
(b) Wiedząc, że
-
26- i 52-tygodniowe bony skarbowe są sprzedawane i kupowane z dyskontem 5 i odpowiednio 8,
-
cena czysta obligacji o czasie trwania 18 miesięcy, która płaci 10% kupon raz w roku, wynosi 90,
oblicz wartość czynnika dyskontowego dla okresu 2Y oraz zerokuponową stopę procentową
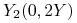 (kapitalizowaną półrocznie, ACT/360).
(kapitalizowaną półrocznie, ACT/360). -
Ćwiczenie 2.12
Dane są następujące wielkości
-
cena 3M bonu skarbowego – 97,
-
cena 9M bonu skarbowego – 92,
-
cena czysta obligacji o czasie trwania 15M z półrocznym 6% kuponem – 95,
-
cena czysta obligacji o czasie trwania 21M z półrocznym 8% kuponem – 94.
Spółka wuwu.com emituje obligację o czasie trwania 18M, która
będzie płacić kupon w wysokości 2.5 kwartalnie. Stopa dochodowości
obligacji emitowanych przez spółki z sektora .com jest
średnio wyższa o 200 punktów bazowych niż stopa dochodowości
papierów skarbowych o podobnej strukturze. Przy tym założeniu wyceń
obligację spółki wuwu.com.
Uwagi: (i) Przyjmij że stopy procentowe obligacji, o których mowa w zadaniu, są podane na bazie 30/360. (ii) Przy poprawnym rozwiązywaniu tego zadania zajdzie potrzeba obliczenia stopy dochodowości. W tym celu możesz się posłużyć np. arkuszem kalkulacyjnym. Sprawdź jak by się zmieniła cena obligacji gdybyś ,,uprościł” rozwiązanie tak by nie obliczać stopy dochodowości, a obliczając cenę tej obligacji po prostu nałożył ten spread na strukturę stóp zerokuponowych.
Ćwiczenie 2.13 (Duracja vel średni czas trwania.)
Rozpatrzmy strumień (portfel) przepływów pieniężnych
![]() (następujących w tej samej walucie) i
załóżmy, że jego wartość w chwili
(następujących w tej samej walucie) i
załóżmy, że jego wartość w chwili ![]()
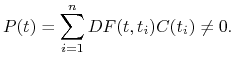 |
Wówczas, możemy określić wielkość
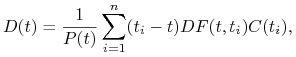 |
którą zwykle określa się jako durację Macaulay'a (ang. Macaulay duration).
-
(a) Pokaż, że jeżeli wszystkie przepływy pieniężne
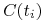 są dodatnie,
to
są dodatnie,
to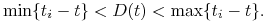
-
(b) Niech
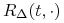 oznacza strukturę stóp procentowych
oznacza strukturę stóp procentowych
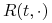 kapitalizowanych w sposób ciągły przesuniętą
równolegle o wielkość
kapitalizowanych w sposób ciągły przesuniętą
równolegle o wielkość  , to znaczy
, to znaczy
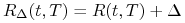 dla każdego
dla każdego 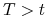 . Niech
. Niech 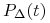 oznacza wartość strumienia
oznacza wartość strumienia 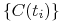 obliczoną przy tak
przesuniętej strukturze stóp, to jest, dla czynników dyskontowych
określonych wzorem
obliczoną przy tak
przesuniętej strukturze stóp, to jest, dla czynników dyskontowych
określonych wzorem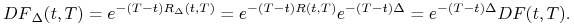
Pokaż, że
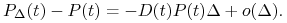 Wskazówka:
Wskazówka:Określ funkcję
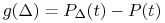 dla ustalonej struktury
stóp
dla ustalonej struktury
stóp 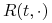 . Oblicz
. Oblicz 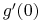 .
. -
(c) Rozpatrzmy teraz zależność wartości strumienia od wielkości równoległego przesunięcia stóp
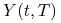 kapitalizowanych
rocznie. Niech
kapitalizowanych
rocznie. Niech 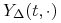 oznacza strukturę stóp
procentowych
oznacza strukturę stóp
procentowych 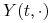 przesuniętą równolegle o wielkość
przesuniętą równolegle o wielkość
 , to znaczy
, to znaczy 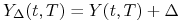 dla każdego
dla każdego 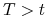 .
Niech
.
Niech 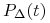 oznacza wartość strumienia
oznacza wartość strumienia 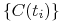 obliczoną przy tak przesuniętej strukturze stóp, to jest, dla
czynników dyskontowych określonych wzorem
obliczoną przy tak przesuniętej strukturze stóp, to jest, dla
czynników dyskontowych określonych wzorem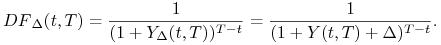
Pokaż, że
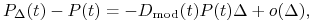
gdzie
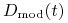 jest tak zwaną zmodyfikowaną duracją Macaulay'a
(ang. modified Macaulay duration) określoną wzorem
jest tak zwaną zmodyfikowaną duracją Macaulay'a
(ang. modified Macaulay duration) określoną wzorem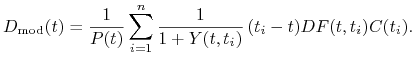
-
(d) Rozpatrzmy teraz przypadek, gdy struktura stóp procentowych jest płaska, to znaczy kiedy
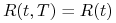 dla każdego
dla każdego 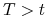 i analogicznie
i analogicznie
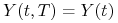 dla
dla 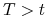 , gdzie oczywiście
, gdzie oczywiście 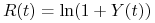 . Pokaż,
że wówczas
. Pokaż,
że wówczas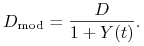
Uwaga: W praktyce duracje obligacji oblicza się względem wewnętrznej stopy zwrotu tej obligacji. Oznacza to, że, na przykład, jeśli do obliczenia wewnętrznej stopy zwrotu przyjęto mechanizm rocznej kapitalizacji, to czynniki dyskontowe
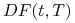 w definicji
duracji (zmodyfikowanej) są postaci
w definicji
duracji (zmodyfikowanej) są postaci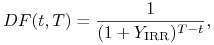
gdzie
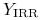 jest wewnętrzną stopą zwrotu tej obligacji (o
rocznej kapitalizacji). Gdy dla wewnętrznej stopy zwrotu przyjęto
inny mechanizm kapitalizacji, np. kapitalizację ciągłą lub półroczną
(przypadek obligacji amerykańskich), to wówczas należy odpowiednio
adaptować definicję czynnika dyskontowego użytego do obliczenia
duracji i sam wzór na durację. Jak widać tak określona duracja nie
jest pojęciem jednolitym, w tym sensie, że zależy ona od wewnętrznej
stopy zwrotu obligacji (łącznie z całym bagażem konwencji użytych do
określenia tej stopy). Trudno jest więc porównywać tak liczone
duracje dla różnych obligacji, szczególnie tych których wewnętrzne
stopy zwrotu różnią się istotnie.
jest wewnętrzną stopą zwrotu tej obligacji (o
rocznej kapitalizacji). Gdy dla wewnętrznej stopy zwrotu przyjęto
inny mechanizm kapitalizacji, np. kapitalizację ciągłą lub półroczną
(przypadek obligacji amerykańskich), to wówczas należy odpowiednio
adaptować definicję czynnika dyskontowego użytego do obliczenia
duracji i sam wzór na durację. Jak widać tak określona duracja nie
jest pojęciem jednolitym, w tym sensie, że zależy ona od wewnętrznej
stopy zwrotu obligacji (łącznie z całym bagażem konwencji użytych do
określenia tej stopy). Trudno jest więc porównywać tak liczone
duracje dla różnych obligacji, szczególnie tych których wewnętrzne
stopy zwrotu różnią się istotnie. -
(e) BPV to nic innego jak zmiana wartości strumienia (portfela przepływów pieniężnych) odpowiadająca przesunięciu równoległemu struktury stóp procentowych o 1 punkt bazowy (0.01%, od ang. basis point oznaczany jako bp), zwykle w dół. Tak więc
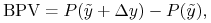
gdzie
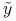 oznacza bieżącą strukturę stóp procentowych, a
oznacza bieżącą strukturę stóp procentowych, a 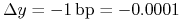 . Wyprowadź związek pomiędzy BPV a duracją.
. Wyprowadź związek pomiędzy BPV a duracją.
Ćwiczenie 2.14 (BPV obligacji zerokuponowej.)
Wyprowadź wzór na BPV obligacji zerokuponowej.
Ćwiczenie 2.15 (Addytywność BPV.)
Niech
gdzie ![]() (przesunięcie tylko
(przesunięcie tylko
![]() tej stopy, to jest stopy o tenorze
tej stopy, to jest stopy o tenorze ![]() ). Pokaż, że
). Pokaż, że
Ćwiczenie 2.16
W portfelu mamy 100 mln PLN (wartości nominalnej) w obligacji o następujących parametrach: 8% kupon płatny co pół roku, termin wykupu za 2 lata i trzy miesiące, YTM (semi-annual, 30/360) wynosi 8.488%. Oblicz
-
(a) cenę czystą tej obligacji,
-
(b) średni czas trwania tej obligacji,
-
(c) zmodyfikowaną durację,
-
(d) przybliżoną zmianę wartości portfela przy wzroście YTM o 5 bp.
Ćwiczenie 2.17
Dealer zarządza dwoma portfelami:
-
portfelem pięcioletnich obligacji zerokuponowych o wartości nominalnej 100 mln PLN,
-
portfelem dwuletnich obligacji zerokuponowych o wartości nominalnej 150 mln PLN.
Dwuletnia stopa zerokuponowa (o rocznej kapitalizacji) wynosi 4%, a pięcioletnia stopa zerokuponowa (o rocznej kapitalizacji) wynosi 5%.
-
(a) Oblicz BPV tych portfeli.
-
(b) Dealer szacuje, że stopa dwuletnia wzrośnie z dnia na dzień o 25 bp a stopa pięcioletnia wzrośnie o 30 bp. Na którym z portfeli dzienna zmiana wyniku będzie większa? Jaka będzie całkowita zmiana wyniku na obu tych portfelach?
-
(c) W drugim scenariuszu dealer szacuje, że stopa dwuletnia wzrośnie z dnia na dzień o 15 bp, a stopa pięcioletnia spadnie o 20 bp. Jaka będzie całkowita zmiana wyniku na obu tych portfelach?
Ćwiczenie 2.18
Dealer zarządza portfelem, którego BPV wynosi -1000 PLN, przy czym
-
BPV odpowiadające zmianie stóp krótkoterminowych (do dwóch lat) wynosi -4000 PLN,
-
BPV odpowiadające zmianie stóp średnioterminowych (miedzy dwoma a pięcioma latami) wynosi 2000 PLN,
-
BPV odpowiadające zmianie stóp długoterminowych (powyżej pięciu lat) wynosi 1000 PLN.
Jak zmieni się wynik na tym portfelu jeśli
-
(a) krzywa stóp procentowych przesunie się równolegle o -25 bp?
-
(b) krzywa stóp procentowych zmieni kąt nachylenia w ten sposób, że stopy krótkoterminowe wzrosną o 10 bp, stopy średnioterminowe nie zmienią się, a stopy długoterminowe spadną o 15 bp?
-
(c) krzywa stóp procentowych zmieni wypukłość w ten sposób, że stopy krótkoterminowe spadną o 5 bp, stopy średnioterminowe wzrosną o 10 bp, a stopy długoterminowe spadną o 15 bp?
Ćwiczenie 2.19 (Duracja portfela.)
Wyprowadź wzór na durację portfela w zależności od duracji składowych portfela.
Ćwiczenie 2.20 (Wynik na lokacie/depozycie.)
Wynik na lokacie (i analogicznie na depozycie) zwykle liczy się
metodą narosłych odsetek. Załóżmy, że bank zrobił lokatę (udzielił
klientowi kredytu) na kwotę ![]() na okres czasu
na okres czasu ![]() . Stopa
oprocentowania lokaty wynosi
. Stopa
oprocentowania lokaty wynosi ![]() , a odsetki w kwocie
, a odsetki w kwocie ![]() będą
zapłacone wraz ze zwrotem ulokowanej kwoty
będą
zapłacone wraz ze zwrotem ulokowanej kwoty ![]() w chwili
w chwili ![]() . Wynik
na tej transakcji w chwili czasu
. Wynik
na tej transakcji w chwili czasu ![]() liczony metodą
narosłych odsetek wynosi
liczony metodą
narosłych odsetek wynosi
gdzie
![]() jest liczbą dni na którą lokata została zrobiona, a
jest liczbą dni na którą lokata została zrobiona, a
![]() jest liczbą dni od początku okresu odsetkowego lokaty do
chwili wyceny
jest liczbą dni od początku okresu odsetkowego lokaty do
chwili wyceny ![]() . Przy założeniu że stopa
. Przy założeniu że stopa ![]() jest na bazie
ACT/365, czyli, że
jest na bazie
ACT/365, czyli, że ![]() , narosłe odsetki możemy
wyrazić w następujący sposób:
, narosłe odsetki możemy
wyrazić w następujący sposób:
gdzie przyjęliśmy, że ![]() . Wynik liczony w powyższy sposób
przyrasta w czasie liniowo i nie zależy od bieżących stóp
procentowych.
. Wynik liczony w powyższy sposób
przyrasta w czasie liniowo i nie zależy od bieżących stóp
procentowych.
Wynik na lokacie (i analogicznie na depozycie) można również liczyć
w sposób ekonomiczny, to znaczy jako wynik który byłby zrealizowany
w rezultacie zamknięcia tej lokaty po stopach obowiązujących w
chwili wyceny ![]() . Tak rozumiany wynik ekonomiczny dany jest wzorem
(dlaczego?)
. Tak rozumiany wynik ekonomiczny dany jest wzorem
(dlaczego?)
Załóżmy, że ![]() – tzn.
– tzn. ![]() jest stopą
depozytową dla okresu
jest stopą
depozytową dla okresu ![]() .
.
Pokaż, że
z
dokładnością do wyrazów drugiego rzędu. Stąd wynika w szczególności,
że jeżeli ![]() , to wynik ekonomiczny pokrywa się (w przybliżeniu)
z wynikiem liczonym metodą narosłych odsetek.
, to wynik ekonomiczny pokrywa się (w przybliżeniu)
z wynikiem liczonym metodą narosłych odsetek.




