Zagadnienia
4. Kontrakty IRS / CCIRS
4.1. Struktura kontraktów wymiany stóp procentowych
Są dwa podstawowe rodzaje kontraktów wymiany stóp procentowych:
-
ang. Interest Rate Swap (IRS):
-
w jednej walucie
-
strony kontraktu wymieniają między sobą (tylko) odsetki
-
-
ang. Cross Currency Interest Rate Swap (CCIRS):
-
w dwóch różnych walutach
-
strony kontraktu wymieniają między sobą odsetki
-
oraz wymieniane są nominały na początku (na ogół, choć nie zawsze) i na końcu kontraktu, oraz w przypadku kontraktu z amortyzacją (ze zmieniającymi się w trakcie trwania kontraktu nominałami) wymieniane są kwoty, które dostosowują odpowiednio nominały kontraktu
-
Kontrakt wymiany procentowej (IRS/CCIRS) składa się z dwóch strumieni pieniężnych, tzw. nóg kontraktu. Strona kontraktu IRS/CCIRS otrzymuje/płaci płatności występujące na jednej nodze kontraktu w zamian za co płaci drugiej stronie/otrzymuje od drugiej strony kontraktu płatności drugiej nogi.
Wyróżniamy dwa rodzaje nóg kontraktów wymiany procentowej:
-
nogę stałą (ang. fixed leg) – odsetki są liczone według stałej stopy,
-
nogę zmienną (ang. floating leg) – odsetki są liczone według zmiennej stopy.
Ze względu na charakter nóg odsetkowych, możemy rozważać następujące typy kontraktów IRS/CCIRS:
-
fixed/float – tzw. coupon swap,
-
float/float – tzw. basis swap,
-
fixed/fixed (ma sens tylko w przypadku kontraktów dwuwalutowych CCIRS).
Ponadto, dla każdego z typów kontraktu IRS/CCIRS możemy mieć kontrakt
-
bez amortyzacji – nominały nóg kontraktu nie zmieniają się w trakcie trwania kontraktu,
-
z amortyzacją – nominały nóg kontraktu zmieniają się w trakcie trwania kontraktu.
Noga stała
Noga stała (ang. fixed leg) kontraktu to strumień płatności
![]() następujących w chwilach
następujących w chwilach ![]() ,
, ![]() (
(![]() jest
terminem zapadalności kontraktu), na który składają się:
jest
terminem zapadalności kontraktu), na który składają się:
-
w przypadku kontraktu IRS, odsetki wyliczone według stałej, ustalonej w kontrakcie, stopy (ang. fixed rate)
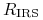
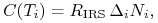
(4.1) gdzie
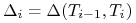 jest długością okresu
odsetkowego
jest długością okresu
odsetkowego 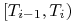 obliczoną według właściwej dla stopy
kontraktu
obliczoną według właściwej dla stopy
kontraktu 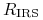 konwencji, a
konwencji, a 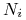 jest nominałem od
którego w okresie odsetkowym
jest nominałem od
którego w okresie odsetkowym 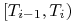 liczone są odsetki;
liczone są odsetki; -
w przypadku kontraktu CCIRS, odsetki wyliczone według stałej, ustalonej w kontrakcie, stopy (ang. fixed rate)
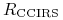 plus,
w przypadku kontraktu o amortyzowanym nominale, przepływy wynikające
z amortyzacji nominału
plus,
w przypadku kontraktu o amortyzowanym nominale, przepływy wynikające
z amortyzacji nominału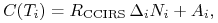
(4.2) gdzie
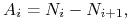
przy czym końcową wypłatę nominału, następującą w
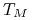 , możemy dla spójności notacji uznać za końcową
amortyzację, to znaczy przyjmiemy, że
, możemy dla spójności notacji uznać za końcową
amortyzację, to znaczy przyjmiemy, że 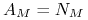 .
.
Noga zmienna
Noga zmienna (ang. floating leg) kontraktu to strumień
płatności ![]() następujących w chwilach
następujących w chwilach ![]() ,
,
![]() (
(![]() jest terminem zapadalności kontraktu),
na które składają się
jest terminem zapadalności kontraktu),
na które składają się
-
w przypadku kontraktu IRS, odsetki wyliczone według, ustalonej w kontrakcie, zmiennej stopy rynkowej (ang. floating rate),
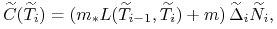
(4.3) gdzie
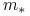 jest czynnikiem multiplikatywnym a
jest czynnikiem multiplikatywnym a 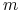 –
marżą addytywną,
–
marżą addytywną, 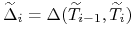 jest długością
okresu odsetkowego
jest długością
okresu odsetkowego 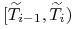 obliczoną według właściwej
dla stopy rynkowej konwencji, a
obliczoną według właściwej
dla stopy rynkowej konwencji, a 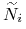 jest nominałem od którego w
okresie odsetkowym
jest nominałem od którego w
okresie odsetkowym 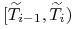 liczone są odsetki,
liczone są odsetki, -
w przypadku kontraktu CCIRS, odsetki wyliczone według, ustalonej w kontrakcie, zmiennej rynkowej stopy (ang. floating rate) plus, w przypadku kontraktu o amortyzowanym nominale, przepływy wynikające z amortyzacji nominału
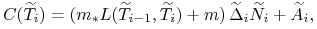
(4.4) gdzie
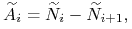
przy czym końcową wypłatę nominału, następującą w
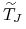 , możemy dla spójności notacji uznać za końcową
amortyzację, to znaczy przyjmiemy, że
, możemy dla spójności notacji uznać za końcową
amortyzację, to znaczy przyjmiemy, że 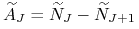 , gdzie
, gdzie
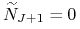 .
.
Uwagi
-
Częstotliwości płatności odsetkowych na obu nogach kontraktu wymiany procentowej nie muszą być takie same. Na przykład, w standardowych (ang. plain vanilla swaps, generic swaps) kontraktach IRS w PLN odsetki nogi stałej są płatne rocznie, a odsetki nogi zmiennej co pół roku po stopie WIBOR 6M.
-
Częstotliwość płatności odsetkowych nogi stałej zwykle jest zgodna ze schematem płatności kuponów obligacji obowiązującym na danym segmencie rynku obligacji (na ogół punktem odniesienia jest rynek obligacji skarbowych), bowiem zgodność ta umożliwia tworzenie dopasowanych strategii zabezpieczających. Jednym z ważnych wyjątków od tej ogólnej reguły są standardowe kontrakty IRS dla USD, które płacą odsetki rocznie, podczas gdy obligacje skarbowe (USD T-bonds) płacą kupon co pół roku.
-
Konwencje stóp procentowych nóg kontraktu IRS/CCIRS nie muszą być takie same i na ogół nie są. I tak:
-
Stopa kontraktu IRS/CCIRS (stopa na nogi stałej) zwykle ma konwencję zgodną z konwencją stóp obligacji o stałym kuponie, choć i tu też są wyjątki od tej ogólnej zasady – noga stała USD IRS jest na bazie ACT/360 podczas gdy USD T-bonds są na bazie ACT/ACT; oraz drugi wyjątek – noga stała EUR IRS ma bazę 30/360 a obligacje rządowe na rynku EU przeszły na konwencję ACT/ACT z chwilą wprowadzenia wspólnej waluty.
-
Stopa zmienna nogi zmiennej ma konwencję rynku pieniężnego danej waluty.
-
-
Na ogół pierwsze okresy odsetkowe na obu nogach kontraktu rozpoczynają się w tym samym momencie.
-
Obie nogi kontraktu wymiany procentowej kończą się w tym samym momencie.
-
Amortyzacje nominałów następują w tych samych chwilach czasu na obu nogach kontraktu.
-
W przypadku kontraktów IRS z amortyzacją nie ma przepływów wynikających ze zmian nominału. Formalnie można by wprowadzić takie przepływy, ale wówczas po zbilansowaniu przepływy te zniosły by się wzajemnie. Jednak czasami, na potrzeby pewnych rozważań i interpretacji będziemy przyjmować, że nogi kontraktu IRS z amortyzacją mają przepływy amortyzacyjne oraz, że następują końcowe wymiany (takich samych) nominałów.
-
W przypadku kontraktów IRS, płatności odsetkowe obu nóg następujące w tej samej chwili czasu są bilansowane i kwota netto rozliczenia jest płacona / otrzymywana.
Kontrakt IRS/CCIRS jako Fixed Bond vs. Floating Rate Note
Zauważmy, że
-
strumień nogi stałej kontraktu IRS/CCIRS (wraz z przepływami wynikającymi z ewentualnych amortyzacji i z nominałem w terminie zapadalności) możemy interpretować jako strumień odpowiedniej obligacji o stałym oprocentowaniu
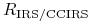 ,
, -
strumień nogi zmiennej kontraktu IRS/CCIRS w którym
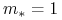 (wraz z przepływami
wynikającymi z ewentualnych amortyzacji i z nominałem w terminie
zapadalności) możemy interpretować jako strumień obligacji o
zmiennym oprocentowaniu.
(wraz z przepływami
wynikającymi z ewentualnych amortyzacji i z nominałem w terminie
zapadalności) możemy interpretować jako strumień obligacji o
zmiennym oprocentowaniu.
Stąd kontrakt IRS w którym, na przykład, otrzymujemy nogę stałą i płacimy nogę zmienną, możemy utożsamiać z portfelem złożonym z kupionej obligacji o stałym kuponie (ang. long fixed bond position) i ze sprzedanej obligacji o zmiennym kuponie (ang. short floating rate note position):
IRS(otrzymujemy ![]() )= + obligacja z kuponem
)= + obligacja z kuponem
![]()
![]() obligacja o zmiennym kuponie
obligacja o zmiennym kuponie
4.2. Wycena kontraktu IRS/CCIRS
Wartość kontraktu IRS/CCIRS (jego wycena) dla strony kontraktu jest
różnicą pomiędzy wyceną nogi otrzymywanej przez stronę a wyceną nogi
płaconej. Wyceną nogi kontraktu w chwili ![]() jest przeliczona po
kursie wymiany (waluty nogi na walutę wyceny) obowiązującym w chwili
jest przeliczona po
kursie wymiany (waluty nogi na walutę wyceny) obowiązującym w chwili
![]() wartość obecna przyszłych w stosunku do
wartość obecna przyszłych w stosunku do ![]() przepływów
pieniężnych tej nogi. Tak więc
przepływów
pieniężnych tej nogi. Tak więc
gdzie
-
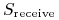 jest kursem wymiany waluty
przepływów nogi otrzymywanej na walutę wyceny,
jest kursem wymiany waluty
przepływów nogi otrzymywanej na walutę wyceny, -
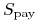 jest kursem wymiany waluty
przepływów nogi płaconej na walutę wyceny.
jest kursem wymiany waluty
przepływów nogi płaconej na walutę wyceny.
Na przykład, dla strony, która otrzymuje odsetki po stopie stałej a płaci odsetki po stopie zmiennej w kontrakcie IRS denominowanym w PLN, wartość kontraktu w PLN wynosi
Przedstawimy wycenę nóg kontraktów wymiany procentowej IRS/CCIRS. Do
wyceny będziemy brać tylko niezrealizowane przepływy nóg
kontraktu, to znaczy te przepływy, które nastąpią w przyszłości
względem momentu wyceny ![]() .
.
Wycena nogi stałej
Niech ![]() będą niezrealizowanymi
przepływami nogi stałej, to znaczy
będą niezrealizowanymi
przepływami nogi stałej, to znaczy ![]() dla każdego
dla każdego
![]() (po ewentualnym przenumerowaniu dat
(po ewentualnym przenumerowaniu dat ![]() , tak by
, tak by
![]() oznaczało pierwszy przyszły termin płatności odsetek). Wartość
nogi stałej kontraktu IRS/CCIRS (wyrażona w walucie tej nogi), to
jest wartość obecna na moment
oznaczało pierwszy przyszły termin płatności odsetek). Wartość
nogi stałej kontraktu IRS/CCIRS (wyrażona w walucie tej nogi), to
jest wartość obecna na moment ![]() strumienia przepływów
strumienia przepływów
![]() , dana jest wzorem:
, dana jest wzorem:
w przypadku kontraktu IRS
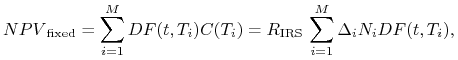 |
(4.5) | ||
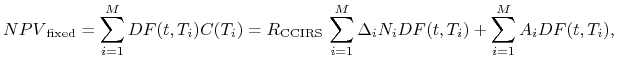 |
gdzie ![]() oznacza czynnik dyskontujący przepływ następujący
w chwili
oznacza czynnik dyskontujący przepływ następujący
w chwili ![]() na moment wyceny
na moment wyceny ![]() odpowiadający strukturze stóp
procentowych waluty nogi kontraktu obowiązującej w dniu wyceny.
odpowiadający strukturze stóp
procentowych waluty nogi kontraktu obowiązującej w dniu wyceny.
Uwaga: W pewnych sytuacjach wyceniając kontrakt IRS do obu nóg kontraktu dokładane są (wzajemnie znoszące się) przepływy amortyzacyjne oraz końcowe wymiany nominałów. Wówczas, wycena tak zmodyfikowanej nogi stałej kontraktu IRS jest dana wzorem (4.5b). W szczególności, dla kontraktów bez amortyzacji (w przypadku IRS z dołożoną końcową wymianą nominałów) mamy
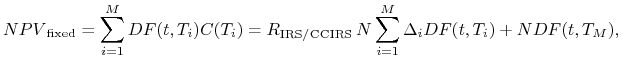 |
(4.6) |
bowiem wtedy ![]() i
i ![]() dla
dla ![]() oraz
oraz ![]() .
Zauważmy, że wówczas (4.6) można interpretować jako wycenę obligacji
o stałym kuponie równym
.
Zauważmy, że wówczas (4.6) można interpretować jako wycenę obligacji
o stałym kuponie równym ![]() .
.
Wycena nogi zmiennej
Aby ujednolicić formuły na wycenę dla kontraktów IRS i CCIRS,
założymy, że w przypadku kontraktów IRS dołożone zostały (wzajemnie
znoszące się) przepływy amortyzacyjne oraz końcowe wymiany
nominałów. Tak samo jak w przypadku wyceny nogi stałej, do wyceny
nogi zmiennej bierzemy tylko niezrealizowane przepływy, to
znaczy te które nastąpią w przyszłości w stosunku do daty wyceny
![]() . Załóżmy, że pierwszym aktualnie trwającym okresem odsetkowym
jest okres
. Załóżmy, że pierwszym aktualnie trwającym okresem odsetkowym
jest okres ![]() , przy czym
, przy czym
![]() , gdzie
, gdzie ![]() jest
datą ustalenia (fixingu) stopy rynkowej na kolejny okres odsetkowy
jest
datą ustalenia (fixingu) stopy rynkowej na kolejny okres odsetkowy
![]() . Wartość rynkowej stopy procentowej
. Wartość rynkowej stopy procentowej
![]() jest znana i w związku z tym przepływ
następujący w chwili
jest znana i w związku z tym przepływ
następujący w chwili ![]() ma dobrze określoną wielkość
ma dobrze określoną wielkość
Z rozważań przeprowadzonych przy omawianiu kontraktów FRA i stóp
forward (patrz Wniosek z Wykładu 3) wynika, że wyceniając przepływy
pieniężne nogi zmiennej (ich części odsetkowe) następujące w
chwilach ![]() możemy zastąpić stopy przyszłe
możemy zastąpić stopy przyszłe
![]() bieżącymi stopami forward, to znaczy stopami
bieżącymi stopami forward, to znaczy stopami
![]() . Wówczas wycena nogi zmiennej (wyrażona w
walucie tej nogi) dana jest wzorem
. Wówczas wycena nogi zmiennej (wyrażona w
walucie tej nogi) dana jest wzorem
| (4.7) |
gdzie przypomnijmy stopa forward ![]() spełnia warunek
spełnia warunek
| (4.8) |
W przypadku, gdy ![]() , stopa
, stopa
![]() dla kolejnego okresu odsetkowego jest również
ustalona na rynku. Wówczas, prócz przepływu następującego w
dla kolejnego okresu odsetkowego jest również
ustalona na rynku. Wówczas, prócz przepływu następującego w ![]() ,
ustaloną wartość ma także przepływ, który nastąpi w
,
ustaloną wartość ma także przepływ, który nastąpi w ![]() . Zatem,
w tym przypadku, wzór na wycenę ma następującą postać
. Zatem,
w tym przypadku, wzór na wycenę ma następującą postać
| (4.9) |
Uproszczone postaci wzorów na wycenę nogi zmiennej
Korzystając z warunku na stopę forward (4.8), wzory
(4.7) i (4.9) możemy przekształcić tak, by nie
zawierały odwołania do stóp forward. Pokażemy to w przypadku, gdy
czynnik multiplikatywny ![]() stopy nogi zmiennej wynosi 1 (wtedy
bowiem wzory te przyjmują szczególnie prostą postać).
stopy nogi zmiennej wynosi 1 (wtedy
bowiem wzory te przyjmują szczególnie prostą postać).
Rozpatrzmy wyrażenia postaci
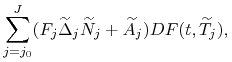 |
(4.10) |
które są składowymi wzoru (4.7) dla ![]() i wzoru
(4.9) dla
i wzoru
(4.9) dla ![]() . Korzystając z definicji stopy forward
(4.8), składniki sumy (4.10) odpowiadające
przepływom odsetkowym możemy przekształcić w następujący sposób
. Korzystając z definicji stopy forward
(4.8), składniki sumy (4.10) odpowiadające
przepływom odsetkowym możemy przekształcić w następujący sposób
Stąd, po uwzględnieniu definicji amortyzacji
![]() , wyrażenia pod sumą (4.10) możemy
zapisać w postaci
, wyrażenia pod sumą (4.10) możemy
zapisać w postaci
Po podstawieniu tych wyrażeń pod znak sumy (4.10) i po
przeprowadzeniu stosownych uproszczeń pamiętając, że ![]() ,
otrzymamy
,
otrzymamy
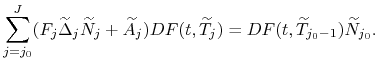 |
(4.11) |
Równość (4.11) wykorzystujemy do uproszczenia wzorów na wycenę nogi zmiennej.
![]() Uproszczona postać wzoru (4.7).
Uproszczona postać wzoru (4.7).
Po wstawieniu (4.11) napisanego w przypadku ![]() do
wzoru (4.7) i przeprowadzeniu stosownych uproszczeń,
otrzymujemy
do
wzoru (4.7) i przeprowadzeniu stosownych uproszczeń,
otrzymujemy
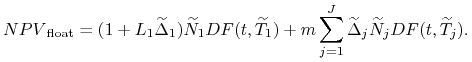 |
(4.12) |
Zauważmy, że wzór (4.12) w przypadku ![]() jest identyczny
ze wzorem na wycenę obligacji o zmiennym kuponie, której okresy
odsetkowe są takie same jak na zmiennej nodze kontraktu IRS.
jest identyczny
ze wzorem na wycenę obligacji o zmiennym kuponie, której okresy
odsetkowe są takie same jak na zmiennej nodze kontraktu IRS.
![]() Uproszczona postać wzoru (4.9).
Uproszczona postać wzoru (4.9).
4.3. Standardowy kontrakt IRS
(ang. plain vanilla IRS, generic IRS)
Na rynku kwotowane są stopy standardowych kontraktów IRS o szerokim zakresie terminów zapadalności: zwykle od 2Y do 10Y, 15Y, 20Y, 30Y oraz czasami 1Y (choć te na ogół mają nieco inną konstrukcję niż kontrakty IRS o dłuższych terminach zapadalności - noga zmienna kontraktu 1Y IRS płaci odsetki z większą częstotliwością niż kontrakty IRS o dłuższych czasach trwania).
Struktura standardowego kontraktu IRS jest następująca:
-
jednowalutowy,
-
wymiana samych odsetek: fixed/float,
-
okresy odsetkowe nogi stałej mają taką samą długość: zwykle rok (dla PLN, USD, EUR), lub pół roku (dla GBP, JPY),
-
bez marż nakładanych na stopę nogi zmiennej:
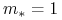 oraz
oraz
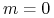 ,
, -
bez amortyzacji: nominał jest stały w trakcie trwania kontraktu,
-
obie nogi zaczynają (i kończą) się w tych samych chwilach czasu.
Wycena standardowego kontraktu IRS (receive: fixed, pay: float)
Wycenę standardowego kontraktu IRS w chwili
![]() uzyskujemy stosując wzór
(4.6) do wyceny nogi stałej oraz wzór (4.12) z
uzyskujemy stosując wzór
(4.6) do wyceny nogi stałej oraz wzór (4.12) z
![]() i
i ![]() do wyceny nogi zmiennej. Aby zastosować te wzory
do przepływów nóg tego kontraktu dołożyliśmy w terminie zapadalności
kontraktu
do wyceny nogi zmiennej. Aby zastosować te wzory
do przepływów nóg tego kontraktu dołożyliśmy w terminie zapadalności
kontraktu ![]() dwa wzajemnie znoszące się przepływy
odpowiadające końcowym wymianom nominałów
dwa wzajemnie znoszące się przepływy
odpowiadające końcowym wymianom nominałów ![]() . Stąd wycena
standardowego kontraktu IRS dana jest wzorem
. Stąd wycena
standardowego kontraktu IRS dana jest wzorem
| (4.14) |
Standardowy kontrakt IRS w chwili zawarcia kontraktu
Rozpatrzmy wycenę standardowego kontraktu IRS w chwili zawarcia
kontraktu. Wówczas data wyceny ![]() (będąca chwilą zawarcia
kontraktu) jest równocześnie chwilą ustalenia stopy zmiennej
(będąca chwilą zawarcia
kontraktu) jest równocześnie chwilą ustalenia stopy zmiennej
![]() dla pierwszego okresu odsetkowego nogi
zmiennej, to jest
dla pierwszego okresu odsetkowego nogi
zmiennej, to jest ![]() , a
, a ![]() jest
bieżącą datą spot. Wartość kontraktu w chwili
jest
bieżącą datą spot. Wartość kontraktu w chwili ![]() dana jest wzorem
(4.14), pomimo tego że wyceniamy kontrakt w dacie
dana jest wzorem
(4.14), pomimo tego że wyceniamy kontrakt w dacie
![]() ustalenia stopy rynkowej
ustalenia stopy rynkowej ![]() dla pierwszego
okresu odsetkowego nogi zmiennej
dla pierwszego
okresu odsetkowego nogi zmiennej ![]() (bowiem w
(bowiem w
![]() nie ma płatności nogi zmiennej). Z własności stopy
nie ma płatności nogi zmiennej). Z własności stopy ![]() i sposobu wyznaczania czynników dyskontowych z kwotowań stóp
depozytowych wynika, że
i sposobu wyznaczania czynników dyskontowych z kwotowań stóp
depozytowych wynika, że
Wtedy wzór (4.14) możemy zapisać w postaci
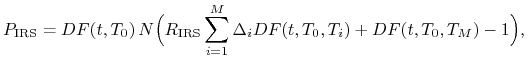 |
(4.15) |
gdzie oznaczyliśmy
| (4.16) |
Czynniki dyskontowe
występujące w
(4.15), określone wzorem (4.16), są czynnikami
(obserwowanymi w chwili bieżącej ![]() ) dyskontującymi do daty spot.
) dyskontującymi do daty spot.
Stopa standardowego kontraktu IRS
Standardowy kontrakt IRS jest zawierany ze stopą ![]() dobraną tak by wartość kontraktu w chwili jego zawarcia wynosiła
zero (strony kontraktu IRS nie ponoszą kosztów początkowych
zawierając kontrakt). Ze wzoru (4.15) wynika, że stopa
dobraną tak by wartość kontraktu w chwili jego zawarcia wynosiła
zero (strony kontraktu IRS nie ponoszą kosztów początkowych
zawierając kontrakt). Ze wzoru (4.15) wynika, że stopa
![]() spełnia równanie
spełnia równanie
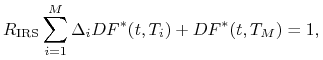 |
(4.17) |
skąd stopa ta wynosi
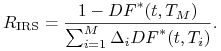 |
Zauważmy, że warunek (4.17) oznacza, że obligacja o stałym
oprocentowaniu ![]() z terminem wykupu
z terminem wykupu ![]() , która płaci
odsetki z taką samą częstotliwością jak noga stała kontraktu IRS,
jest at par, to znaczy, cena tej obligacji jest równa jej
wartości nominalnej. Stąd, stopy kontraktów IRS mogą być traktowane
jako punkt odniesienia przy określaniu oprocentowania nowo
emitowanych obligacji stałokuponowych.
, która płaci
odsetki z taką samą częstotliwością jak noga stała kontraktu IRS,
jest at par, to znaczy, cena tej obligacji jest równa jej
wartości nominalnej. Stąd, stopy kontraktów IRS mogą być traktowane
jako punkt odniesienia przy określaniu oprocentowania nowo
emitowanych obligacji stałokuponowych.
Uwaga 4.1
Stopę ![]() niestandardowego kontraktu IRS/CCIRS na
ogół wyznacza się również tak, by wartość tego kontraktu w chwili
zawarcia wynosiła zero.
niestandardowego kontraktu IRS/CCIRS na
ogół wyznacza się również tak, by wartość tego kontraktu w chwili
zawarcia wynosiła zero.
Stopa standardowego kontraktu IRS jako średnia stóp forward
Znów rozpatrzmy standardowy kontrakt IRS, w którym odsetki po obu nogach są płacone z taką samą częstotliwością. Ponieważ wartość kontraktu w chwili jego zawarcia wynosi zero, to
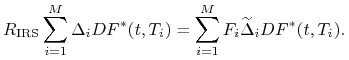 |
(4.18) |
Zatem,
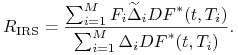 |
(4.19) |
Ze wzoru (4.19) wynika, że jeśli stopy forward i stopa
![]() są wyrażane w tej samej konwencji, czyli gdy
są wyrażane w tej samej konwencji, czyli gdy
![]() dla każdego
dla każdego ![]() , to
, to
Ponadto, jak widać z (4.19), stopa ![]() jest
średnią ważoną stóp
jest
średnią ważoną stóp ![]() . Jako przykład, weźmy dwuletni kontrakt
IRS z odsetkami płaconymi co pół roku po obu nogach. Ponieważ
. Jako przykład, weźmy dwuletni kontrakt
IRS z odsetkami płaconymi co pół roku po obu nogach. Ponieważ
wzór (4.19) oznacza, że stopa
![]() jest, w przybliżeniu, średnią ważoną czynnikami
dyskontowymi, obserwowalnych na rynku: stopy LIBOR 6M oraz stóp FRA
na kolejne 6-miesięczne okresy.
jest, w przybliżeniu, średnią ważoną czynnikami
dyskontowymi, obserwowalnych na rynku: stopy LIBOR 6M oraz stóp FRA
na kolejne 6-miesięczne okresy.
Standardowy kontrakt IRS vs. seria kontraktów FRA
Rozpatrzmy standardowy kontrakt IRS, w którym odsetki po obu nogach są płacone z taką samą częstotliwością. Wówczas taki kontrakt jest serią wymian odsetek
-
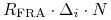 w chwili
w chwili 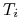 ,
, -
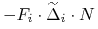 w chwili
w chwili 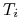 .
.
Każda taka wymiana (za wyjątkiem pierwszej) może być potraktowana
jako syntetyczne przepływy (sprzedanego) kontraktu
FRA![]() ze stopą
ze stopą ![]() . Pierwsza
wymiana w kontrakcie IRS jest wymianą odsetek według stopy
. Pierwsza
wymiana w kontrakcie IRS jest wymianą odsetek według stopy
![]() za odsetki według ustalonej już rynkowej stopy
referencyjnej. Tak więc wartość takiego kontraktu IRS jest taka sama
jak wartość serii sprzedanych kontraktów FRA
za odsetki według ustalonej już rynkowej stopy
referencyjnej. Tak więc wartość takiego kontraktu IRS jest taka sama
jak wartość serii sprzedanych kontraktów FRA![]() ,
,
![]() , FRA
, FRA![]() z taką samą stopą równą
z taką samą stopą równą
![]() oraz pierwszej wymiany odsetek. Warto zauważyć, że
te kontrakty FRA mają na ogół nierynkową stopę (ang.
off-market), wszystkie taką samą równą
oraz pierwszej wymiany odsetek. Warto zauważyć, że
te kontrakty FRA mają na ogół nierynkową stopę (ang.
off-market), wszystkie taką samą równą ![]() .
.
4.4. Bootstrapping czynników dyskontowych
W praktyce wzór (4.17) stosuje się raczej do wyznaczenia
wartości czynników dyskontowych niż do wyznaczania stóp kontraktów
IRS, bowiem to właśnie na podstawie kwotowań stóp standardowych
kontraktów IRS wyznacza się strukturę stóp procentowych i czynników
dyskontowych. Niech ![]() oznacza stopę standardowego kontraktu IRS,
który zapada w
oznacza stopę standardowego kontraktu IRS,
który zapada w ![]() . Terminy zapadalności standardowych kontraktów
IRS, w których odsetki nogi stałej są płacone rocznie, są
,,wielokrotnościami lat”, co zaznaczamy pisząc
. Terminy zapadalności standardowych kontraktów
IRS, w których odsetki nogi stałej są płacone rocznie, są
,,wielokrotnościami lat”, co zaznaczamy pisząc ![]() (gdzie
(gdzie ![]() symbolizuje okres roczny, a
symbolizuje okres roczny, a ![]() jest liczbą naturalną). W przypadku
gdy odsetki nogi stałej są płacone co pół roku, terminy zapadalności
tych kontraktów są ,,wielokrotnościami sześciomiesięcznych okresów”
i wówczas
jest liczbą naturalną). W przypadku
gdy odsetki nogi stałej są płacone co pół roku, terminy zapadalności
tych kontraktów są ,,wielokrotnościami sześciomiesięcznych okresów”
i wówczas ![]() , gdzie
, gdzie ![]() .
.
Przekształcając (4.17) otrzymujemy
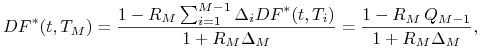 |
(4.20) |
gdzie oznaczyliśmy
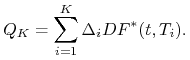 |
Wzór (4.20) stosujemy rekurencyjnie przy założeniu, że mamy
już wyznaczony (innymi metodami) czynnik dyskontowy ![]() .
Zauważmy również, że aby rekurencja była możliwa musimy założyć, że
końce okresów odsetkowych kontraktu IRS użytego w (4.20) są
zgodne z terminami zapadalności poprzednich kontraktów i wówczas
mamy związek
.
Zauważmy również, że aby rekurencja była możliwa musimy założyć, że
końce okresów odsetkowych kontraktu IRS użytego w (4.20) są
zgodne z terminami zapadalności poprzednich kontraktów i wówczas
mamy związek
Powyższe równanie ułatwia przeprowadzenie rekurencyjnych obliczeń wartości czynników dyskontowych.
Problem gładkości stóp forward
Jakość zbudowanej krzywej czynników dyskontowych (zerokuponowych
stóp procentowych) jest oceniana na podstawie przebiegu
implikowanych z tej krzywej stóp forward. Jednym z kryteriów takiej
oceny jest gładkość (regularność) względem ![]() stóp forward
stóp forward
![]() o pewnym ustalonym tenorze
o pewnym ustalonym tenorze ![]() .
.
Na gładkość stóp forward wpływ mają
-
wartości danych wejściowych użytych do wyznaczenia czynników dyskontowych – te przyczyny można uznać za obiektywne,
-
sposoby uzupełniania brakujących danych wejściowych, np. interpolacje stóp par,
-
metody interpolacji i ekstrapolacji czynników dyskontowych,
-
założenia odnośnie postaci funkcjonalnej krzywej czynników dyskontowych i sposobu jej estymacji.
Wyznaczanie krzywej czynników dyskontowych o gładkich stopach forward
Stopy forward implikowane z krzywej swapowej otrzymanej przez bootstrapping często mają nieregularny przebieg, który nie ma ekonomicznego uzasadnienia. Poniżej opiszemy sposób wyznaczania krzywej swapowej która dokładnie wycenia kontrakty IRS i dla której stopy implikowane zmieniają się w sposób regularny.
Idea wyznaczania takiej krzywej jest następująca
-
czynniki dyskontowe są wyznaczane przez stopy forward o ustalonym relatywnie krótkim tenorze (np. trzy miesiące), które dobieramy tak, by
-
kontrakty IRS były prawidłowo wycenione przez tą krzywą,
-
stopy forward zmieniały się w sposób regularny.
Oznaczenia:
-
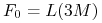 – znana (z rynku) stopa typu LIBOR dla okresu 3M
– znana (z rynku) stopa typu LIBOR dla okresu 3M -
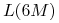 – znana (z rynku) stopa typu LIBOR dla okresu 6M
– znana (z rynku) stopa typu LIBOR dla okresu 6M -
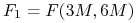 – stopa forward implikowana ze znanych (z rynku) stóp
– stopa forward implikowana ze znanych (z rynku) stóp 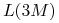 oraz
oraz
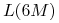 ; alternatywnie zamiast korzystać ze stopy
; alternatywnie zamiast korzystać ze stopy 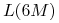 można za
można za
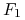 przyjąć stopę kontraktu FRA3x6
przyjąć stopę kontraktu FRA3x6 -
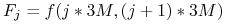 dla
dla 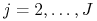 – szukane 3M stopy
forward dla kolejnych 3M okresów począwszy od 6M
– szukane 3M stopy
forward dla kolejnych 3M okresów począwszy od 6M -
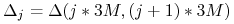 – długość okresu depozytowego stopy
– długość okresu depozytowego stopy 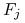
-
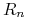 – rynkowe kwotowania stóp wybranego zestawu
– rynkowe kwotowania stóp wybranego zestawu 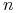 -letnich kontraktów IRS,
to jest dla
-letnich kontraktów IRS,
to jest dla 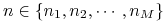
Stopy forward ![]() (
(![]() ) znajdujemy rozwiązując
następujący problem optymalizacyjny
) znajdujemy rozwiązując
następujący problem optymalizacyjny
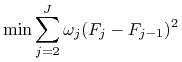 |
(4.21) |
pod warunkiem, że dla każdego ![]() zachodzi
zachodzi
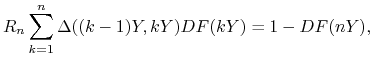 |
(4.22) |
gdzie czynniki dyskontowe są obliczone następującym wzorem rekurencyjnym
| (4.23) |
przy czym
W wyrażeniu
(4.21) ![]() są wagami, które określają relatywny
wpływ poszczególnych składników na wartość sumy. Zwykle przyjmuje
się, że
są wagami, które określają relatywny
wpływ poszczególnych składników na wartość sumy. Zwykle przyjmuje
się, że ![]() dla każdego
dla każdego ![]() . Wartość sumy (4.21)
mierzy stopień zmienności (wahanie) stóp forward. Im ta wartość jest
mniejsza, tym stopy zmieniają się w bardziej regularny sposób.
Dobierając wagi
. Wartość sumy (4.21)
mierzy stopień zmienności (wahanie) stóp forward. Im ta wartość jest
mniejsza, tym stopy zmieniają się w bardziej regularny sposób.
Dobierając wagi ![]() w specyficzny sposób, możemy wymusić w
której części krzywej stopy forward zachowują się regularnie a w
której dopuszczamy większe wahania tych stóp.
w specyficzny sposób, możemy wymusić w
której części krzywej stopy forward zachowują się regularnie a w
której dopuszczamy większe wahania tych stóp.
Warunek (4.22) gwarantuje, że kontrakty IRS z wybranego zestawu są poprawnie wyceniane przez krzywą. W odróżnieniu do standardowego bootstrappingu, zestaw kontraktów IRS nie musi się składać ze wszystkich kolejnych kontraktów. Zagadnienie optymalizacyjne (4.21) – (4.22) rozwiązuje się stosując standardowe algorytmy numeryczne, na przykład metodę gradientów sprzężonych lub metodę Newtona (dostępne w narzędziu Solver arkusza kalkulacyjnego MS Excel).
Możliwe są jeszcze inne warianty powyższej metody. Na przykład,
-
Wtedy w powyższym zadaniu zmieniamy tylko sposób wyznaczania czynników dyskontowych na następujący
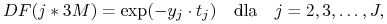
a stopy forward występujące w (1) obliczamy wzorem
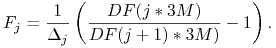
4.5. Własności stóp kontraktów IRS
Korzystając ze związku (4.17) dla kontraktu IRS zapadalnego
w ![]() , który zapisaliśmy w postaci
, który zapisaliśmy w postaci
wyrażenie (4.18) możemy przedstawić w postaci
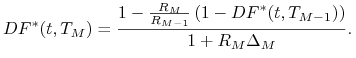 |
(4.24) |
Ze wzoru (4.24) wynikają dwa warunki na poprawność
struktury czynników dyskontowych. Mianowicie, warunek
![]() oznacza, że stopa
oznacza, że stopa ![]() kontraktu IRS musi
spełniać nierówność
kontraktu IRS musi
spełniać nierówność
| (4.25) |
Z warunku na monotoniczność czynników dyskontowych
![]() otrzymujemy natomiast następujące
ograniczenie
otrzymujemy natomiast następujące
ograniczenie
| (4.26) |
Korzystając z tych dwóch warunków, można pokazać (Zadanie 4.6), że
jeśli ![]() dla
dla ![]() oraz gdy
ciąg stóp
oraz gdy
ciąg stóp ![]() jest ograniczony, to
jest ograniczony, to
| (4.27) |
Zagadnienia i zadania na Ćwiczenia
Ćwiczenie 4.1 (Terminowy kontrakt IRS (ang. forward starting IRS))
W terminowym kontrakcie IRS rozpoczęcie okresów odsetkowych następuje w przyszłości w stosunku do daty spot dla daty zawarcia kontraktu (inaczej: data ustalenia wartości rynkowej stopy dla pierwszego okresu odsetkowego nogi zmiennej znajduje się w przyszłości w stosunku do daty zawarcia kontraktu).
-
(a) Wyceń standardowy kontrakt terminowy IRS w chwili
 która znajduje się
przed rozpoczęciem okresów odsetkowych kontraktu.
która znajduje się
przed rozpoczęciem okresów odsetkowych kontraktu. -
(b) Przy założeniu, że wartość tego kontraktu w chwili jego zawarcia wynosi zero, znajdź wzór na wartość stopy tego kontraktu.
Ćwiczenie 4.2
Wyprowadź wzory uproszczone na wycenę nogi zmiennej kontraktu
IRS/CCIRS bez założenia ![]() .
.
Ćwiczenie 4.3
(a) Dane są następujące wielkości:
-
sześciomiesięczna stopa depozytowa wynosi 6.00%,
-
kwotowania kontraktów FRA na przyszłą stopę procentową wynoszą
FRA6x12 – 6.20%, FRA12x18 – 6.30%,
-
stopa dwuletniego kontraktu IRS wynosi 6.50%,
-
ceny obligacji zerokuponowych, które zapadają za dwa i pół roku oraz za trzy lata, wynoszą odpowiednio
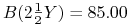 oraz
oraz
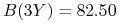 .
.
Wyznacz wartości czynników dyskontowych dla okresów czasu będących
wielokrotnościami sześciomiesięcznych okresów do trzech lat
włącznie. W obliczeniach, dla uproszczenia, przyjmij, że długość
![]() -miesięcznego okresu czasu (
-miesięcznego okresu czasu (![]() ) wynosi
) wynosi
![]() lat.
lat.
(b) Rozpatrzmy jednowalutowy kontrakt wymiany procentowej typu fixed/float ze zmiennym nominałem o czasie trwania 3 lata. W trakcie trwania kontraktu nominał kontraktu jest redukowany o 20% początkowej wartości (tj. wartości w chwili zawarcia) po każdym rocznym okresie odsetkowym. Odsetki po stronie stałej (fixed leg) są płacone co roku, a po stronie zmiennej (float leg) co pół roku.
Przy danych rynkowych podanych w punkcie (a) oblicz stopę stałej strony kontraktu, przy której wartość tego kontraktu w chwili zawarcia wynosi zero.
Ćwiczenie 4.4 (Rollercoaster swap)
Firma Y ma dług od którego płaci odsetki po stopie WIBOR 6M plus 50
bp marży. Struktura tego długu jest następująca: w pierwszym roku
nominał długu wynosi 50 mln PLN, w drugim 80 mln PLN, w trzecim 100
mln PLN, w czwartym 60 mln PLN, i ostatnim piątym roku 40 mln PLN.
Firma Y chce zrestrukturyzować płatności odsetkowe od tego długu w
ten sposób by przez pięć lat płacić stopę WIBOR 6M powiększoną o
marżę ![]() od stałego nominału w wysokości 65 mln PLN. W tym celu
firma Y zawiera z bankiem X odpowiedni kontrakt IRS. Jaką minimalną
wartość marży
od stałego nominału w wysokości 65 mln PLN. W tym celu
firma Y zawiera z bankiem X odpowiedni kontrakt IRS. Jaką minimalną
wartość marży ![]() Bank X powinien zakwotować firmie Y? W celu
wykonania obliczeń przyjmij, że stopy kontraktów IRS (annual,
ACT/365) wynoszą: 1Y – 5.50%, 2Y – 5.60%, 3Y – 5.70%, 4Y –
5.90%, 5Y – 6.00%, oraz dla uproszczenia obliczeń załóż, że
każdy roczny okres ma 365 dni.
Bank X powinien zakwotować firmie Y? W celu
wykonania obliczeń przyjmij, że stopy kontraktów IRS (annual,
ACT/365) wynoszą: 1Y – 5.50%, 2Y – 5.60%, 3Y – 5.70%, 4Y –
5.90%, 5Y – 6.00%, oraz dla uproszczenia obliczeń załóż, że
każdy roczny okres ma 365 dni.
Ćwiczenie 4.5 (Asset swap)
Rozpatrzmy dwuletnią obligację, która płaci co pół roku kupon według
stopy zmiennej ![]() (typu LIBOR) powiększonej o marżę
(typu LIBOR) powiększonej o marżę ![]() . Cena tej
obligacji wynosi 101. Inwestor jest skłonny kupić tą obligację pod
warunkiem że jednocześnie będzie mógł zawrzeć kontrakt IRS, który
zamieni odsetki otrzymywane z tej obligacji na odsetki liczone
według stopy stałej, przy czym stopa tego kontraktu IRS powinna być
tak dobrana by cały pakiet (obligacja plus kontrakt IRS) był
at par.
. Cena tej
obligacji wynosi 101. Inwestor jest skłonny kupić tą obligację pod
warunkiem że jednocześnie będzie mógł zawrzeć kontrakt IRS, który
zamieni odsetki otrzymywane z tej obligacji na odsetki liczone
według stopy stałej, przy czym stopa tego kontraktu IRS powinna być
tak dobrana by cały pakiet (obligacja plus kontrakt IRS) był
at par.
-
(a) Oblicz wysokość marży
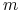 .
. -
(b) Oblicz wysokość stopy kontraktu IRS.
-
(c) Oblicz oprocentowanie stałego kuponu, który w efekcie nabycia tego pakietu (asset swapa) będzie otrzymywał inwestor.
Do obliczeń użyj następującej krzywej czynników dyskontowych
Ćwiczenie 4.6
Pokaż, że jeśli ![]() dla
dla ![]() oraz gdy ciąg stóp
oraz gdy ciąg stóp ![]() jest ograniczony, to
jest ograniczony, to
![]() przy
przy ![]() .
.
Ćwiczenie 4.7
Niech ![]() oznacza stopę
oznacza stopę ![]() -letniego kontraktu IRS, który zapada w
-letniego kontraktu IRS, który zapada w
![]() .
.
-
(a) Pokaż, że
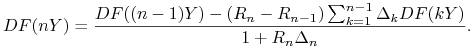
-
(b) Korzystając z wyniku punktu (a), pokaż, że jeśli
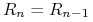 , to stopa prosta forward
dla okresu czasu
, to stopa prosta forward
dla okresu czasu ![[(n-1)Y,nY]](wyklady/ifi/mi/mi423.png) wynosi
wynosi 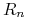 .
. -
(c) W szczególności, pokaż, że jeśli struktura stóp procentowych kontraktów IRS jest płaska, tzn.
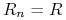 dla każdego
dla każdego
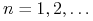 , to proste stopy forward
, to proste stopy forward 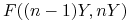 są takie same
dla każdego
są takie same
dla każdego 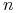 i wynoszą
i wynoszą 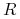 . Ponadto, pokaż że wówczas
. Ponadto, pokaż że wówczas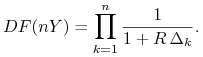
Jeśli założyć dodatkowo, że
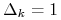 dla każdego
dla każdego 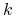 , to powyższy wzór
przyjmuje szczególnie czytelną postać, mianowicie
, to powyższy wzór
przyjmuje szczególnie czytelną postać, mianowicie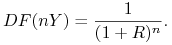
Ćwiczenie 4.8
-
(a) Inverse floater (bull floater)
Inverse floater to papier wartościowy, w którym kupon jest liczony według stopy
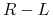 , gdzie
, gdzie 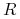 jest stałą stopą, a
jest stałą stopą, a 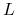 zmienną stopą rynkową (typu LIBOR, WIBOR), i oczywiście w terminie
zapadalności zwraca nominał. Zwykle, stopa
zmienną stopą rynkową (typu LIBOR, WIBOR), i oczywiście w terminie
zapadalności zwraca nominał. Zwykle, stopa 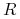 jest istotnie większa
niż stopa
jest istotnie większa
niż stopa 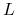 ustalona na rynku w chwili emisji papieru i jest
dobierana tak by w chwili emisji papier był at par. Ile
powinna wynosić stopa
ustalona na rynku w chwili emisji papieru i jest
dobierana tak by w chwili emisji papier był at par. Ile
powinna wynosić stopa 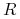 ?
? -
(b) Bear floater
Bear floater to papier wartościowy, w którym kupon jest liczony według stopy
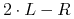 , gdzie
, gdzie 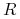 jest stałą stopą, a
jest stałą stopą, a 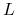 zmienną stopą rynkową (typu LIBOR, WIBOR) ,i oczywiście w terminie
zapadalności zwraca nominał. Zwykle, stopa
zmienną stopą rynkową (typu LIBOR, WIBOR) ,i oczywiście w terminie
zapadalności zwraca nominał. Zwykle, stopa 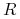 jest dobierana tak by
w chwili emisji papier był at par. Ile powinna wynosić
stopa
jest dobierana tak by
w chwili emisji papier był at par. Ile powinna wynosić
stopa 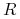 ?
?
Uwaga: W praktyce zwykle warunki inverse floater i
bear floater ograniczają z dołu kupon tak by miał on zawsze
nieujemną wartość. Wówczas, wyznaczając stopę ![]() należy uwzględnić
koszt opcji gwarantującej nieujemność kuponu. Wrócimy do tego
problemu w wykładzie 12.
należy uwzględnić
koszt opcji gwarantującej nieujemność kuponu. Wrócimy do tego
problemu w wykładzie 12.
Ćwiczenie 4.9
Rozpatrzmy standardowy kontrakt IRS (receive fixed) o rezydualnym
czasie trwania ![]() lat, który był zawarty ze stopą
lat, który był zawarty ze stopą ![]() . Bieżące
kwotowanie standardowego kontraktu IRS
. Bieżące
kwotowanie standardowego kontraktu IRS ![]() Y (pay fixed) wynosi
Y (pay fixed) wynosi
![]() . Pokaż, że koszt przedterminowego zamknięcia zawartego
kontraktu (na jednostkę nominału) wynosiłby
. Pokaż, że koszt przedterminowego zamknięcia zawartego
kontraktu (na jednostkę nominału) wynosiłby
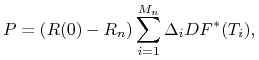 |
gdzie ![]() oznacza ułamek roku
oznacza ułamek roku ![]() tego okresu odsetkowego
nogi stałej kontraktu,
tego okresu odsetkowego
nogi stałej kontraktu, ![]() koniec tego okresu, a
koniec tego okresu, a ![]() jest liczbą
okresów odsetkowych nogi stałej,
jest liczbą
okresów odsetkowych nogi stałej, ![]() jest czynnikiem
dyskontującym do daty spot.
jest czynnikiem
dyskontującym do daty spot.
Ćwiczenie 4.10
Rozpatrzmy kontrakt IRS (pay fixed annual / receive float semi-annual) o zmiennym nominale o rezydualnym czasie trwania 3 lata zawarty ze stopa 5.00%. Nominał tego kontraktu IRS w ciągu kolejnych trzech lat jest następujący: w 1 roku – 120 mln PLN, w 2 roku – 80 mln PLN, w 3 roku – 100 mln PLN. Bieżące kwotowanie standardowego kontraktu IRS 3Y (fixed annual / float semi-annual) wynosi 5.00%. Czy zamykając w chwili bieżącej kontrakt IRS zrealizujemy zysk czy stratę?




