13. Model Marczuka humoralnej odpowiedzi odpornościowej
Kolejny wykład poświęcimy na zapoznanie się z nieco bardziej skomplikowanym modelem odpowiedzi odpornościowej. W 1975 r. Guri I. Marczuk (właściwie G. I. Marchuk według obowiązującej transkrypcji rosyjskiego nazwiska, Marczuk to spolszczona wersja tego nazwiska) zaproponował dość prosty model, który jest w stanie odzwierciedlić najważniejsze przebiegi odpowiedzi odpornościowej, w tym również chorobę przewlekłą (chroniczną). Model opisany jest za pomocą czterech równań z opóźnionym argumentem i z założenia odzwierciedla humoralną odpowiedź odpornościową, choć podobną strukturę modelu można także zaproponować w przypadku odpowiedzi komórkowej. Model ten będziemy w dalszym ciągu nazywać modelem Marczuka. W 1980 r. ukazała się książka Marczuka [14], w której oprócz tego najprostszego modelu przedstawił także kilka wersji bardziej rozbudowanych, w tym model opisujący równoległy przebieg odpowiedzi humoralnej i komórkowej. W późniejszych latach ukazały się także tłumaczenia tej książki na język angielski [11] i polski [12]. Wyniki doświadczalne dla pewnych chorób okazały się bardzo podobne do teoretycznych wyników uzyskanych na podstawie modelu Marczuka.
Z powstaniem modelu wiąże się ciekawa historia. Marczuk przez wiele lat był przewodniczącym Akademii Nauk ZSSR. Niestety zachorował na żółtaczkę zakaźną, a pobyt w szpitalu urozmaicał sobie poznawaniem mechanizmów odpornościowych. W rezultacie doprowadziło to do powstania modelu reakcji odpornościowej i zaowocowało wieloma pracami naukowymi w tej dziedzinie. Po powrocie do zdrowia Marczuk w dalszym ciągu prowadził działalność naukową, w ramach której odwiedził Wydział Matematyki, Informatyki i Mechaniki UW, gdzie zaprezentował model i wyniki symulacji wskazujące możliwości leczenia choroby przewlekłej za pomocą zaostrzenia infekcji. Zarówno sam model, jak i możliwości jego zastosowania, zafascynowały jednego z pionierów polskiej biomatematyki, prof. Wiesława Szlenka. Tematyka ta znalazła się później wśród zagadnień badawczych w powstałym po pewnym czasie Instytucie Matematyki Stosowanej i Mechaniki.
13.1. Prezentacja modelu Marczuka
Zajmiemy się teraz omówieniem konstrukcji prostego modelu odpowiedzi odpornościowej zaproponowanego przez G. I. Marczuka, a następnie przedstawimy podstawowe własności układu.
Przypomnijmy, że reakcja odpornościowa następuje w wyniku wniknięcia do organizmu obcego czynnika, który nazywamy antygenem. W przypadku omawianego modelu antygenem są głównie bakterie, ponieważ np. wirusy wywołują znacznie bardziej skomplikowane reakcje, które wymagają bardziej skomplikowanego opisu matematycznego, w szczególności uwzględnienia także komórkowej odpowiedzi odpornościowej. Pojawienie się antygenu wywołuje kaskadę reakcji, które w efekcie doprowadzają do rozpoznania antygenu i uruchomienia produkcji przeciwciał swoistych przez komórki plazmatyczne. Mechanizmem uruchamiającym tę kaskadę jest powstanie tzw. kompleksu VT, czyli przyłączenie do antygenu przeciwciała prezentującego. Wobec tego zakładamy, że produkcja komórek plazmatycznych zależy od liczby wiązań antygen – przeciwciało, przy czym obserwujemy opóźnienie między powstaniem takiego wiązania a wyprodukowaniem przed układ odpornościowy komórek plazmatycznych produkujących przeciwciała swoiste.
W modelu występują następujące podstawowe zmienne
-
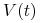 — zagęszczenie populacji bakterii (antygenu) w organizmie
w chwili
— zagęszczenie populacji bakterii (antygenu) w organizmie
w chwili 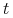 ,
, -
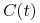 — zagęszczenie komórek plazmatycznych w chwili
— zagęszczenie komórek plazmatycznych w chwili 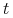 ,
, -
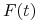 — stężenie przeciwciał w chwili
— stężenie przeciwciał w chwili 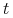 ,
,
przy czym (jak dotychczas) używamy określenia zagęszczenie w stosunku do osobników pewnej populacji (tu populacji komórkowych), natomiast stężenie dotyczy głównie substancji, a wiemy, że przeciwciała są białkami.
Dynamikę antygenu opisujemy w modelu Marczuka w taki sam sposób jak w najprostszym modelu odpowiedzi odpornościowej prezentowanym poprzednio. Zakładamy, że bakterie rozmnażają się za stałym współczynnikiem reprodukcji ![]() i giną w wyniku reakcji odpornościowych. Zatem śmiertelność spowodowana jest wiązaniem antygenów z przeciwciałami, proporcjonalnie do liczby tych
wiązań ze współczynnikiem
i giną w wyniku reakcji odpornościowych. Zatem śmiertelność spowodowana jest wiązaniem antygenów z przeciwciałami, proporcjonalnie do liczby tych
wiązań ze współczynnikiem ![]() , który odzwierciedla prawdopodobieństwo związania antygenu z przeciwciałem i siłę ich reakcji.
Stąd
, który odzwierciedla prawdopodobieństwo związania antygenu z przeciwciałem i siłę ich reakcji.
Stąd
Przeciwciała giną nie tylko w wyniku wiązania z antygenem, ale też w procesie naturalnej degradacji. Są one produkowane przez komórki plazmatyczne w stałym tempie ![]() , czyli
, czyli
gdzie ![]() opisuje frakcję związanych przeciwciał ginących w reakcji odpornościowej, a
opisuje frakcję związanych przeciwciał ginących w reakcji odpornościowej, a ![]() odzwierciedla średni czas przetrwania
przeciwciała.
odzwierciedla średni czas przetrwania
przeciwciała.
Zauważyliśmy wcześniej, że produkcja komórek plazmatycznych uruchamiana jest przez powstanie kompleksów
![]() i jest opóźniona w stosunku do mechanizmu uruchamiającego.
Dla uproszczenia zakładamy, że opóźnienie to jest stałe, równe
i jest opóźniona w stosunku do mechanizmu uruchamiającego.
Dla uproszczenia zakładamy, że opóźnienie to jest stałe, równe ![]() .
W organizmie utrzymuje się też stały fizjologiczny poziom przeciwciał
.
W organizmie utrzymuje się też stały fizjologiczny poziom przeciwciał ![]() . Skoro tak, to jeśli nie ma antygenu, wewnętrzną dynamikę komórek plazmatycznych możemy opisać równaniem
. Skoro tak, to jeśli nie ma antygenu, wewnętrzną dynamikę komórek plazmatycznych możemy opisać równaniem
gdzie ![]() oznacza średnią długość życia komórki plazmatycznej.
Wtedy
oznacza średnią długość życia komórki plazmatycznej.
Wtedy ![]() przy
przy ![]() , co oznacza, że w zdrowym organizmie po odchyleniu od poziomu fizjologicznego zawsze następuje samoczynny powrót do tego poziomu.
, co oznacza, że w zdrowym organizmie po odchyleniu od poziomu fizjologicznego zawsze następuje samoczynny powrót do tego poziomu.
Jeśli antygen występuje w organizmie, to w powyższym równaniu uwzględniamy jeszcze składnik związany ze stymulacją odpowiedzi odpornościowej
przy czym ![]() jest współczynnikiem immunogenności antygenu odzwierciedlającym siłę odpowiedzi odpornościowej na dany antygen.
jest współczynnikiem immunogenności antygenu odzwierciedlającym siłę odpowiedzi odpornościowej na dany antygen.
Prócz tych trzech podstawowych zmiennych w modelu występuje zmienna dodatkowa, która opisuje stopień uszkodzenia organu zaatakowanego przez antygen, ponieważ Marczuk budował swój model z myślą o żółtaczce i stopniu uszkodzenia wątroby w wyniku tej choroby.
Niech ![]() oznacza charakterystykę (masę lub powierzchnię) zdrowego organu, a
oznacza charakterystykę (masę lub powierzchnię) zdrowego organu, a ![]() — zdrową część organu uszkodzonego przez antygen. Definiujemy
— zdrową część organu uszkodzonego przez antygen. Definiujemy
Mamy zatem ![]() , co opisuje stosunek części uszkodzonej do całości. Oczywiście
, co opisuje stosunek części uszkodzonej do całości. Oczywiście
![]() dla organu zdrowego oraz
dla organu zdrowego oraz ![]() dla organu całkowicie zniszczonego. Dynamikę
dla organu całkowicie zniszczonego. Dynamikę ![]() opisujemy za pomocą prostego równania liniowego
opisujemy za pomocą prostego równania liniowego
gdzie ![]() odzwierciedla zdolność antygenu do niszczenia organu, a
odzwierciedla zdolność antygenu do niszczenia organu, a ![]() oznacza średni czas regeneracji organu.
oznacza średni czas regeneracji organu.
Wielkość ![]() osłabia odpowiedź odpornościową poprzez zmniejszenie stymulacji produkcji komórek plazmatycznych, zatem zamiast współczynnika immunogenności
osłabia odpowiedź odpornościową poprzez zmniejszenie stymulacji produkcji komórek plazmatycznych, zatem zamiast współczynnika immunogenności ![]() rozpatrujemy w modelu współczynnik
rozpatrujemy w modelu współczynnik ![]() , gdzie
, gdzie ![]() jest nierosnącą funkcją zmiennej
jest nierosnącą funkcją zmiennej ![]() ,
, ![]() i
i ![]() .
.
Ostatecznie model Marczuka humoralnej odpowiedzi odpornościowej opisujemy układem 4. równań różniczkowych z opóźnionym argumentem (rrzoa)
![\begin{array}[]{l c l}\dot{V}(t)&=&(\beta-\gamma F(t))V(t),\\
\dot{C}(t)&=&\alpha\xi(m(t))V(t-\tau)F(t-\tau)-\mu _{C}(C(t)-C^{{*}}),\\
\dot{F}(t)&=&\varrho C(t)-(\mu _{F}+\eta\gamma V(t))F(t),\\
\dot{m}(t)&=&\sigma V(t)-\mu _{m}m(t)\ \ \mbox{dla}\ \ m(t)\leq 1.\end{array}](wyklady/mbm/mi/mi1154.png) |
(13.1) |
W większości przypadków istnieje pewna progowa wielkość ![]() , do której
, do której ![]() nie wpływa znacząco na reakcję odpornościową i można założyć, że
nie wpływa znacząco na reakcję odpornościową i można założyć, że ![]() dla
dla ![]() .
.
13.2. Podstawowe własności układu (13.1)
Przejdziemy teraz do zbadania podstawowych własności układu (13.1). Jest on układem równań z opóźnionym argumentem, zatem jako warunek początkowy należy zadać funkcję określoną na odcinku ![]() o wartościach w
o wartościach w ![]() . Ponieważ jednak tylko współrzędne
. Ponieważ jednak tylko współrzędne
![]() i
i ![]() występują z opóźnionym argumentem, więc możemy zadać tylko ich wartości na całym przedziale
występują z opóźnionym argumentem, więc możemy zadać tylko ich wartości na całym przedziale ![]() , ograniczając się do wartości
, ograniczając się do wartości ![]() i
i ![]() dla zmiennych
dla zmiennych ![]() i
i ![]() . Należy przy tym pamiętać, że z
formalnego punktu widzenia potrzebne są wszystkie cztery współrzędne funkcji początkowej.
. Należy przy tym pamiętać, że z
formalnego punktu widzenia potrzebne są wszystkie cztery współrzędne funkcji początkowej.
Istnienie, jednoznaczność i nieujemność rozwiązań dla nieujemnego warunku początkowego możemy wykazać stosując metodę kroków. Przypomnijmy, że opiera się ona na zasadzie indukcji matematycznej i pozwala zastosować znane techniki dotyczące równań różniczkowych zwyczajnych do analizy rrzoa.
Istnienie lokalnego rozwiązania układu (13.1).
Niech ![]() ,
, ![]() . Wtedy dla
. Wtedy dla ![]() układ (13.1) sprowadza się do niejednorodnego układu rrz postaci
układ (13.1) sprowadza się do niejednorodnego układu rrz postaci
![\begin{array}[]{l c l}\dot{V}(t)&=&(\beta-\gamma F(t))V(t),\\
\dot{C}(t)&=&\alpha\xi(m(t))G_{0}(t)-\mu _{C}(C(t)-C^{{*}}),\\
\dot{F}(t)&=&\varrho C(t)-(\mu _{F}+\eta\gamma V(t))F(t),\\
\dot{m}(t)&=&\sigma V(t)-\mu _{m}m(t)\ \ \mbox{dla}\ \ m(t)\leq 1,\end{array}](wyklady/mbm/mi/mi1237.png) |
(13.2) |
gdzie ![]() jest znaną funkcją, gdyż dla
jest znaną funkcją, gdyż dla
![]() argument
argument ![]() . Funkcje
opisujące współrzędne prawej strony układu (13.2)
są wielomianami kwadratowym względem współrzędnych, czyli są klasy
. Funkcje
opisujące współrzędne prawej strony układu (13.2)
są wielomianami kwadratowym względem współrzędnych, czyli są klasy ![]() (faktycznie
(faktycznie ![]() ), więc spełniają założenia twierdzeń o lokalnym istnieniu i jednoznaczności rozwiązań równań różniczkowych zwyczajnych. Istnieje zatem odcinek
), więc spełniają założenia twierdzeń o lokalnym istnieniu i jednoznaczności rozwiązań równań różniczkowych zwyczajnych. Istnieje zatem odcinek ![]() , na którym mamy jednoznaczne rozwiązanie układu.
, na którym mamy jednoznaczne rozwiązanie układu.
Nieujemność lokalnego rozwiązania układu (13.1).
Pokażemy najpierw, że rozwiązanie to jest nieujemne. Pierwsze równanie układu (13.2) zapisujemy w równoważnej postaci całkowej
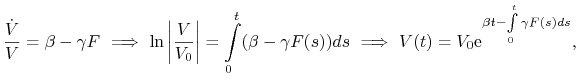 |
gdzie w powyższym wzorze ![]() .
Zatem
.
Zatem ![]() dla
dla ![]() , co więcej,
, co więcej,
![]() dla
dla ![]() , czyli z matematycznego punktu widzenia wyzdrowienie może wystąpić tylko asymptotycznie. W praktyce zagęszczenie antygenu niższe od czułości urządzeń pomiarowych jest niewykrywalne i takie zagęszczenia uznajemy za równoważne wyzdrowieniu.
, czyli z matematycznego punktu widzenia wyzdrowienie może wystąpić tylko asymptotycznie. W praktyce zagęszczenie antygenu niższe od czułości urządzeń pomiarowych jest niewykrywalne i takie zagęszczenia uznajemy za równoważne wyzdrowieniu.
Dla ![]() drugie równanie układu (13.2) jest równaniem liniowym niejednorodnym. Rozwiązujemy je stosując metodę uzmienniania
stałej i otrzymujemy
drugie równanie układu (13.2) jest równaniem liniowym niejednorodnym. Rozwiązujemy je stosując metodę uzmienniania
stałej i otrzymujemy
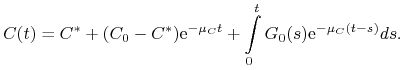 |
(13.3) |
Ponieważ ![]() oraz
oraz ![]() dla
dla ![]() , to
, to ![]() dla
dla ![]() .
Zauważmy też, że
w tym przypadku współrzędna
.
Zauważmy też, że
w tym przypadku współrzędna ![]() jest zdefiniowana za pomocą wzoru (13.3) na całym przedziale
jest zdefiniowana za pomocą wzoru (13.3) na całym przedziale ![]() .
.
W ogólnym przypadku, gdy ![]() ,
oszacujemy wartość pochodnej
,
oszacujemy wartość pochodnej ![]() z dołu przez
z dołu przez ![]() , więc
, więc
Zatem ![]() dla
dla ![]() .
Zauważmy także, że jeśli
.
Zauważmy także, że jeśli ![]() , to z powyższych nierówności
wynika, że
, to z powyższych nierówności
wynika, że ![]() dla dowolnego
dla dowolnego ![]() .
.
W analogiczny sposób dowodzimy nieujemności zmiennej ![]() .
.
Skoro ![]() dla
dla ![]() , to
podobnie oszacujemy
, to
podobnie oszacujemy ![]() , czyli
, czyli
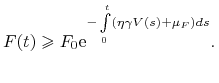 |
Zatem ![]() dla
dla ![]() .
.
Istnienie rozwiązania układu (13.1) na przedziale ![[0,\tau]](wyklady/mbm/mi/mi1160.png) .
.
Pokażemy teraz, że z nieujemności rozwiązań wynika ich istnienie na całym przedziale ![]() . W tym celu oszacujemy nasze rozwiązania z góry.
Dla pierwszej zmiennej mamy
. W tym celu oszacujemy nasze rozwiązania z góry.
Dla pierwszej zmiennej mamy
zatem wzrost ![]() jest co najwyżej wykładniczy.
jest co najwyżej wykładniczy.
Dla zmiennej ![]() mamy
mamy
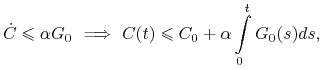 |
czyli ![]() jest również ograniczona na każdym podprzedziale odcinka
jest również ograniczona na każdym podprzedziale odcinka
![]() .
.
Z ograniczoności ![]() i
i ![]() wynika ograniczoność
wynika ograniczoność
![]() i
i ![]() . Skoro funkcje te są ograniczone, więc ograniczone są także ich pochodne, czyli rozwiązanie można przedłużyć biorąc jako nowy warunek początkowy granicę
. Skoro funkcje te są ograniczone, więc ograniczone są także ich pochodne, czyli rozwiązanie można przedłużyć biorąc jako nowy warunek początkowy granicę ![]() (istnienie granicy wynika bezpośrednio z ograniczoności pochodnej) oraz punkt
(istnienie granicy wynika bezpośrednio z ograniczoności pochodnej) oraz punkt ![]() i stosując twierdzenie o istnieniu rozwiązań. Wobec dowolności
i stosując twierdzenie o istnieniu rozwiązań. Wobec dowolności ![]() wnioskujemy, że rozwiązanie istnieje na całym
wnioskujemy, że rozwiązanie istnieje na całym ![]() .
.
Globalne istnienie rozwiązań układu (13.1).
Stosując metodę kroków zakładamy, że istnieje nieujemne rozwiązanie
układu (13.1) na odcinku ![]() i powtarzamy powyższe rozumowanie w celu wykazania istnienia nieujemnego rozwiązania na kolejnym
odcinku
i powtarzamy powyższe rozumowanie w celu wykazania istnienia nieujemnego rozwiązania na kolejnym
odcinku ![]() . Na mocy zasady indukcji matematycznej
jednoznaczne, nieujemne rozwiązanie układu (13.1)
istnieje dla dowolnego
. Na mocy zasady indukcji matematycznej
jednoznaczne, nieujemne rozwiązanie układu (13.1)
istnieje dla dowolnego ![]() .
.
Punkty krytyczne układu (13.1).
Znajdziemy teraz punkty krytyczne badanego układu. Rozwiązujemy następujący układ równań algebraicznych
![\begin{array}[]{l c l}0&=&(\beta-\gamma\bar{F})\bar{V},\\
0&=&\alpha\xi(\bar{m})\bar{V}\bar{F}-\mu _{C}(\bar{C}-C^{{*}}),\\
0&=&\varrho\bar{C}-(\mu _{F}+\eta\gamma\bar{V})\bar{F},\\
0&=&\sigma\bar{V}-\mu _{m}\bar{m}.\end{array}](wyklady/mbm/mi/mi1239.png) |
(13.4) |
W ogólnym przypadku, aby rozwiązać układ (13.4), musimy zadać konkretną postać funkcji ![]() .
Dla uproszczenia załóżmy więc, że
.
Dla uproszczenia załóżmy więc, że ![]() , czyli
, czyli ![]() . W tym przypadku badanie możemy ograniczyć do układu trzech równań, a następnie sprawdzić zachowanie ostatniej zmiennej.
. W tym przypadku badanie możemy ograniczyć do układu trzech równań, a następnie sprawdzić zachowanie ostatniej zmiennej.
Łatwo widać, że układ (13.4) ma rozwiązanie opisujące stan zdrowia, czyli ![]() i
i ![]() . Wtedy
. Wtedy ![]() i oczywiście
i oczywiście ![]() .
. ![]() nazwiemy poziomem fizjologicznym przeciwciał.
nazwiemy poziomem fizjologicznym przeciwciał.
Niech ![]() odzwierciedla stan zdrowia organizmu.
odzwierciedla stan zdrowia organizmu.
Jeśli ![]() , to z pierwszego równania układu (13.4) mamy
, to z pierwszego równania układu (13.4) mamy
![]() . Wstawiając tę zależność do drugiego i trzeciego równania obliczmy
. Wstawiając tę zależność do drugiego i trzeciego równania obliczmy
Punkt krytyczny ![]() odzwierciedla chorobę przewlekłą, oczywiście pod warunkiem, że wszystkie jego współrzędne są dodatnie.
Współrzędne
odzwierciedla chorobę przewlekłą, oczywiście pod warunkiem, że wszystkie jego współrzędne są dodatnie.
Współrzędne ![]() i
i ![]() możemy przepisać w nieco innej postaci
możemy przepisać w nieco innej postaci
z czego wynika, że jeśli
-
[A.]
-
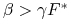 i
i 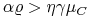 albo
albo -
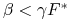 i
i 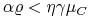 ,
,
to ![]() .
Zauważmy dalej, że przy warunku A mamy:
.
Zauważmy dalej, że przy warunku A mamy:
| (13.5) |
zatem ![]() . Przy warunku B nierówność (13.5) zmienia znak, ale znak zmienia też mianownik
. Przy warunku B nierówność (13.5) zmienia znak, ale znak zmienia też mianownik ![]() , czyli
, czyli ![]() . Widzimy więc, że warunki A, B są konieczne i dostateczne dla istnienia dodatniego punktu krytycznego. Zauważmy także, że w tym przypadku
. Widzimy więc, że warunki A, B są konieczne i dostateczne dla istnienia dodatniego punktu krytycznego. Zauważmy także, że w tym przypadku ![]() oraz
oraz ![]() .
Ostatnia nierówność oznacza, że w omawianym przypadku
.
Ostatnia nierówność oznacza, że w omawianym przypadku ![]() poziom stacjonarny antygenu
poziom stacjonarny antygenu ![]() nie może być zbyt duży. W literaturze mówi się o lekkiej chorobie przewlekłej dla
nie może być zbyt duży. W literaturze mówi się o lekkiej chorobie przewlekłej dla ![]() , natomiast gdy
, natomiast gdy ![]() — o ciężkiej.
— o ciężkiej.
Lokalna stabilność punktów krytycznych układu (13.1).
Badanie lokalnej stabilności punktów krytycznych rrzoa nie różni się w początkowej fazie od analogicznej analizy dla rrz. Niech ![]() oznacza punkt krytyczny. Zdefiniujmy nowe zmienne:
oznacza punkt krytyczny. Zdefiniujmy nowe zmienne: ![]() ,
, ![]() ,
,
![]() . Układ w nowych zmiennych ma postać
. Układ w nowych zmiennych ma postać
![\begin{array}[]{l c l}\dot{v}(t)&=&(\beta-\gamma\tilde{F}-\gamma f(t))v(t)-\gamma\tilde{V}f(t),\\
\dot{c}(t)&=&\alpha(\tilde{V}f(t-\tau)+\tilde{F}v(t-\tau)+v(t-\tau)f(t-\tau))-\mu _{C}c(t),\\
\dot{f}(t)&=&\varrho c(t)-\mu _{F}f(t)-\eta\gamma(\tilde{F}v(t)+\tilde{V}f(t)+v(t)f(t)).\\
\end{array}](wyklady/mbm/mi/mi1182.png) |
(13.6) |
Linearyzujemy układ (13.6) wokół punktu ![]() zakładając, że
zakładając, że ![]() ,
, ![]() ,
,
![]() dla
dla ![]() .
Składniki wyższego rzędu, czyli
.
Składniki wyższego rzędu, czyli
![]() i
i ![]() szacują się przez
szacują się przez ![]() , co
możemy pominąć. Po zlinearyzowaniu układ (13.6) przyjmuje postać
, co
możemy pominąć. Po zlinearyzowaniu układ (13.6) przyjmuje postać
![\begin{array}[]{l c l}\dot{v}(t)&=&(\beta-\gamma\tilde{F})v(t)-\gamma\tilde{V}f(t),\\
\dot{c}(t)&=&\alpha(\tilde{V}f(t-\tau)+\tilde{F}v(t-\tau))-\mu _{C}c(t),\\
\dot{f}(t)&=&\varrho c(t)-\mu _{F}f(t)-\eta\gamma(\tilde{F}v(t)+\tilde{V}f(t)).\\
\end{array}](wyklady/mbm/mi/mi1206.png) |
(13.7) |
W kolejnym kroku znajdujemy rozwiązania układu (13.7) postaci ![]() ,
, ![]() ,
,
![]() . Otrzymujemy więc następujące zależności
. Otrzymujemy więc następujące zależności
![\begin{array}[]{l c l}0&=&(-\lambda+\beta-\gamma\tilde{F})v_{0}-\gamma\tilde{V}f_{0},\\
0&=&\alpha\tilde{F}v_{0}\text{e}^{{-\lambda\tau}}+\alpha\tilde{V}f_{0}\text{e}^{{-\lambda\tau}}-(\mu _{C}+\lambda)c_{0},\\
0&=&-\eta\gamma\tilde{F}v_{0}+\varrho c_{0}-(\eta\gamma\tilde{V}+\mu _{F}+\lambda)f_{0}.\\
\end{array}](wyklady/mbm/mi/mi1196.png) |
(13.8) |
Układ (13.8) ma nietrywialne rozwiązania, jeśli
![\det\left(\begin{array}[]{c c c}\beta-\gamma\tilde{F}-\lambda&0&-\gamma\tilde{V}\\
\alpha\tilde{F}\text{e}^{{-\lambda\tau}}&-\mu _{C}-\lambda&\alpha\tilde{V}\text{e}^{{-\lambda\tau}}\\
-\eta\gamma\tilde{F}&\varrho&-\eta\gamma\tilde{V}-\mu _{F}-\lambda\\
\end{array}\right)=0.](wyklady/mbm/mi/mi1177.png) |
(13.9) |
Twierdzenie o linearyzacji gwarantuje, że jeśli wartości własne, czyli rozwiązania równania (13.8) mają części rzeczywiste ujemne, to rozwiązanie ![]() układu (13.6) jest lokalnie asymptotycznie stabilne, natomiast jeśli istnieje wartość własna o części rzeczywistej dodatniej, to rozwiązanie jest niestabilne.
układu (13.6) jest lokalnie asymptotycznie stabilne, natomiast jeśli istnieje wartość własna o części rzeczywistej dodatniej, to rozwiązanie jest niestabilne.
Zbadamy wartości własne dla poszczególnych punktów krytycznych. Zaczniemy od ![]() . Wtedy macierz układu ma postać dolnietrójkątną, zatem łatwo wyznaczamy wartości własne, gdyż spełniają równanie
. Wtedy macierz układu ma postać dolnietrójkątną, zatem łatwo wyznaczamy wartości własne, gdyż spełniają równanie
czyli wartości własne są równe: ![]() ,
,
![]() ,
, ![]() , zatem są rzeczywiste i ujemne dla
, zatem są rzeczywiste i ujemne dla
![]() .
.
Wniosek 13.1
Jeśli ![]() , to rozwiązanie
, to rozwiązanie ![]() jest lokalnie asymptotycznie stabilne. Natomiast jeśli
jest lokalnie asymptotycznie stabilne. Natomiast jeśli ![]() , to
, to ![]() jest niestabilne.
jest niestabilne.
Widzimy, że stabilność rozwiązania ![]() , czyli wyzdrowienie jest możliwe tylko przy niewielkiej reproduktywność antygenu
, czyli wyzdrowienie jest możliwe tylko przy niewielkiej reproduktywność antygenu ![]() w stosunku do poziomu fizjologicznego przeciwciał
w stosunku do poziomu fizjologicznego przeciwciał ![]() .
.
Badając stabilność rozwiązania ![]() otrzymujemy następujący pseudowielomian charakterystyczny
otrzymujemy następujący pseudowielomian charakterystyczny
| (13.10) |
gdzie
| (13.11) |
a wyznaczenie współczynników pozostawiamy jako ćwiczenie. Przypomnijmy, że dla ![]() pseudowielomian ma nieskończenie wiele pierwiastków, co utrudnia jego analizę (podczas gdy dla wielomianów możemy skorzystać np. z kryt. Routha – Hurwitza).
pseudowielomian ma nieskończenie wiele pierwiastków, co utrudnia jego analizę (podczas gdy dla wielomianów możemy skorzystać np. z kryt. Routha – Hurwitza).
Wiemy, że jeśli rozwiązanie
jest stabilne dla ![]() , to z ciągłej zależności od parametrów
wynika, że albo rozwiązanie jest stabilne dla wszystkich
, to z ciągłej zależności od parametrów
wynika, że albo rozwiązanie jest stabilne dla wszystkich ![]() ,
albo istnieje krytyczna wartość parametru
,
albo istnieje krytyczna wartość parametru ![]() , dla której może nastąpić destabilizacja.
Dla
, dla której może nastąpić destabilizacja.
Dla ![]() możemy zbadać stabilność punktu
możemy zbadać stabilność punktu ![]() za pomocą kryterium Routha – Hurwitza, skąd dostajemy warunek stabilności
za pomocą kryterium Routha – Hurwitza, skąd dostajemy warunek stabilności
| (13.12) |
Warunek ![]() jest równoważny
jest równoważny ![]() , zatem stabilność
, zatem stabilność ![]() dla
dla ![]() możliwa jest tylko w przypadku A. Natomiast w przypadku B mamy stabilność punktu
możliwa jest tylko w przypadku A. Natomiast w przypadku B mamy stabilność punktu ![]() .
.
Zauważmy, że zmiana stabilności może nastąpić tylko gdy pseudowielomian charakterystyczny (13.10) ma pierwiastki czysto urojone ![]() . Wtedy
. Wtedy
czyli
Zdefiniujmy funkcję pomocniczą
Jej dodatnie miejsca zerowe determinują potencjalne zmiany stabilności punktu krytycznego ![]() . Z warunku (13.12) wynika, że wyraz wolny wielomianu
. Z warunku (13.12) wynika, że wyraz wolny wielomianu ![]() jest ujemny, zatem istnieje co najmniej jedno dodatnie miejsce zerowe.
Warunek A lub B implikuje też
jest ujemny, zatem istnieje co najmniej jedno dodatnie miejsce zerowe.
Warunek A lub B implikuje też ![]() , czyli dodatnie miejsce zerowe
, czyli dodatnie miejsce zerowe ![]() jest wyznaczone jednoznacznie. Niech
jest wyznaczone jednoznacznie. Niech ![]() , gdzie
, gdzie ![]() . Podstawiając
. Podstawiając ![]() do pseudowielomianu (13.10) dostajemy układ równań, z którego wyznaczamy sinus i kosinus wartości krytycznej
do pseudowielomianu (13.10) dostajemy układ równań, z którego wyznaczamy sinus i kosinus wartości krytycznej ![]() . Mamy zatem krytyczną wartość opóźnienia zdefiniowaną w sposób uwikłany za pomocą tych funkcji trygonometrycznych. Skoro jednak znamy tylko wartości sinusa i kosinusa, to oczywiście mamy nie jedną wartość krytyczną, a cały ciąg takich wartości
. Mamy zatem krytyczną wartość opóźnienia zdefiniowaną w sposób uwikłany za pomocą tych funkcji trygonometrycznych. Skoro jednak znamy tylko wartości sinusa i kosinusa, to oczywiście mamy nie jedną wartość krytyczną, a cały ciąg takich wartości ![]() z pierwszą wartością
z pierwszą wartością ![]() , taką że
, taką że ![]() i
i ![]() .
.
Zmiana stabilności następuje przy takiej krytycznej wartości ![]() , dla której istnieje para czysto urojonych wartości własnych
, dla której istnieje para czysto urojonych wartości własnych ![]() i przy przekraczaniu osi urojonej wartości własne przechodzą z lewej półpłaszczyzny zespolonej na prawą, czyli
i przy przekraczaniu osi urojonej wartości własne przechodzą z lewej półpłaszczyzny zespolonej na prawą, czyli ![]() . Przypomnijmy, że znak tej pochodnej jest taki sam jak znak pochodnej funkcji pomocniczej
. Przypomnijmy, że znak tej pochodnej jest taki sam jak znak pochodnej funkcji pomocniczej ![]() w odpowiednim miejscu zerowym — tutaj jedynym miejscu zerowym
w odpowiednim miejscu zerowym — tutaj jedynym miejscu zerowym ![]() . W tej sytuacji mamy oczywiście dodatnią pochodną
. W tej sytuacji mamy oczywiście dodatnią pochodną ![]() i wartości własne przechodzą z lewej półpłaszczyzny zespolonej na prawą.
i wartości własne przechodzą z lewej półpłaszczyzny zespolonej na prawą.
Wniosek 13.2
Jeśli spełnione są nierówności (13.12) i istnieje dodatni punkt krytyczny ![]() , to punkt ten jest stabilny dla
, to punkt ten jest stabilny dla ![]() i istnieje krytyczna wartość opóźnienia
i istnieje krytyczna wartość opóźnienia ![]() , przy której
, przy której ![]() traci stabilność i pozostaje niestabilny dla
traci stabilność i pozostaje niestabilny dla ![]() . W
. W ![]() zachodzi bifurkacja Hopfa, czyli pojawiają się nietrywialne rozwiązania okresowe o okresie
zachodzi bifurkacja Hopfa, czyli pojawiają się nietrywialne rozwiązania okresowe o okresie ![]() .
.
Przypomnijmy, że z nierówności ![]() wynika, że stabilność punktu
wynika, że stabilność punktu ![]() przy
przy ![]() jest możliwa tylko w przypadku spełnienia warunku A.
jest możliwa tylko w przypadku spełnienia warunku A.
Korzystając z kryterium Michajłowa, można udowodnione następujące twierdzenie dotyczące stabilności punktu ![]() , które daje nam oszacowanie wielkości opóźnienia krytycznego
, które daje nam oszacowanie wielkości opóźnienia krytycznego ![]()
Twierdzenie 13.1
Niech ![]() oraz
oraz
| (13.13) |
Jeśli dodatkowo spełnione są nierówności (13.12) i istnieje dodatni punkt krytyczny ![]() , to punkt ten jest lokalnie asymptotycznie stabilny.
, to punkt ten jest lokalnie asymptotycznie stabilny.
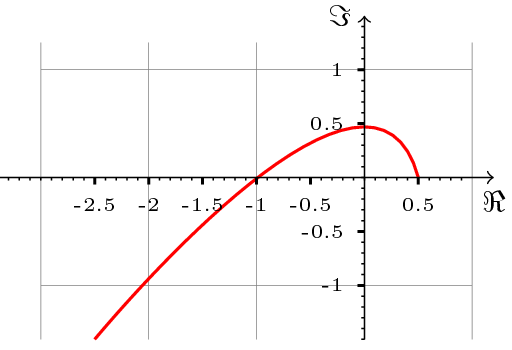
Twierdzenie 13.1 zadaje warunki wystarczające stabilności punktu ![]() przy ustalonych parametrach. Warunki te implikują, że hodograf Michajłowa ma kształt przedstawiony na rys. 13.2.
przy ustalonych parametrach. Warunki te implikują, że hodograf Michajłowa ma kształt przedstawiony na rys. 13.2.
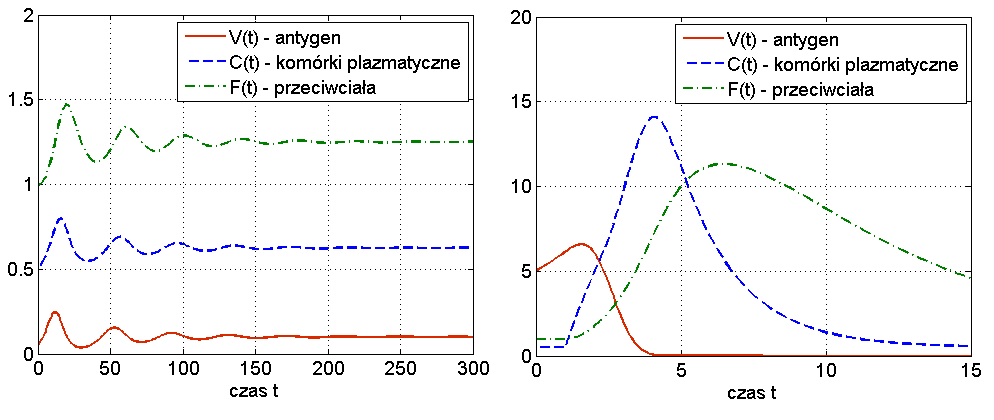
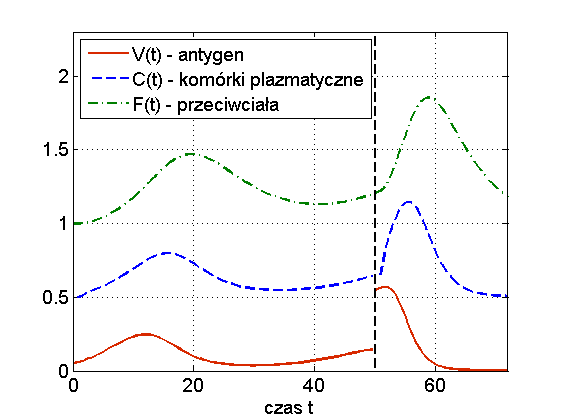
Widzimy więc, że układ (13.1) jest w stanie odzwierciedlić dwa podstawowe przebiegi choroby: zakażenie z wyzdrowieniem oraz chorobę przewlekłą (chroniczną), por. rys. 13.3. Ciekawą własnością symulacji tego modelu jest to, że zwiększając dawkę antygenu możemy wyprowadzić organizm z choroby chronicznej — mówimy o wyzdrowieniu poprzez zaostrzenie choroby, por. rys. 13.4. Trzeba jednak podkreślić, że taki efekt obserwuje się tylko w symulacjach, natomiast wszystkie wyniki analityczne wskazują na globalną stabilność punktu ![]() przy założeniu
przy założeniu ![]() .
.
![Przebieg typowej funkcji $\xi(m)$, czyli funkcja tożsamościowo równa 1 na odcinku $[0,m^{*}]$ oraz malejąca liniowo do 0 na $[m^{*},1]$.](wyklady/mbm/wyk13_przykladowe_eps_od_m.png)