3. Modelowanie pojedynczej populacji III
3.1. Efekt Alleego
W większości przypadków, jeśli nie uwzględniamy migracji, to model pojedynczej populacji ![]() , zarówno w przypadku ciągłym jak i dyskretnym, możemy zapisać w ogólnej postaci
, zarówno w przypadku ciągłym jak i dyskretnym, możemy zapisać w ogólnej postaci
| (3.1) |
gdzie ![]() odzwierciedla przyrost per capita, podobnie jak w przypadku równania logistycznego (2.2). Omówimy teraz postać funkcji
odzwierciedla przyrost per capita, podobnie jak w przypadku równania logistycznego (2.2). Omówimy teraz postać funkcji ![]() w przypadku występowania w populacji tzw. efektu Alleego. Populacje, w których obserwujemy taki efekt, zmniejszają swoją liczebność, jeśli spadnie ona poniżej pewnego progu. Typowo wiążemy efekt Alleego z drapieżnictwem — na dynamikę danej populacji wpływa także to, że w ekosystemie występuje gatunek drapieżnika żywiący się osobnikami populacji
w przypadku występowania w populacji tzw. efektu Alleego. Populacje, w których obserwujemy taki efekt, zmniejszają swoją liczebność, jeśli spadnie ona poniżej pewnego progu. Typowo wiążemy efekt Alleego z drapieżnictwem — na dynamikę danej populacji wpływa także to, że w ekosystemie występuje gatunek drapieżnika żywiący się osobnikami populacji ![]() , przy czym zakładamy, że drapieżników jest zawsze dużo. Wobec tego jeśli liczebność populacji
, przy czym zakładamy, że drapieżników jest zawsze dużo. Wobec tego jeśli liczebność populacji ![]() jest niewielka, to drapieżniki zjadają dostępne osobniki i populacja
jest niewielka, to drapieżniki zjadają dostępne osobniki i populacja ![]() wymiera.
wymiera.
Modele z efektem Alleego mogą mieć różną postać, w zależności od funkcji drapieżnictwa. Najprostszy model stanowi modyfikację równania logistycznego (2.2)
| (3.2) |
gdzie ![]() i
i ![]() interpretujemy analogicznie jak w równaniu logistycznym, natomiast
interpretujemy analogicznie jak w równaniu logistycznym, natomiast ![]() nazywamy w tym kontekście pułapką drapieżnictwa.
nazywamy w tym kontekście pułapką drapieżnictwa.
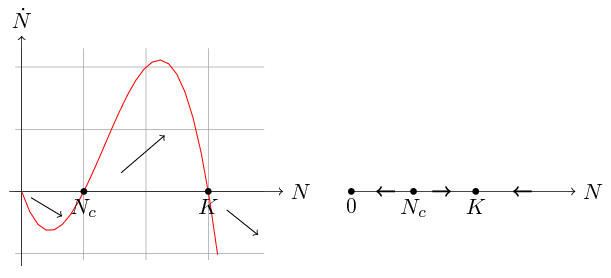
Podobnie jak w przypadku równania (2.2), równanie (3.2) możemy rozwiązać analitycznie rozkładając prawą stronę na ułamki proste, co zostawimy jako ćwiczenie. Najważniejsze własności rozwiązań odczytamy z portretu fazowego, por. rys. 3.1.
Widzimy, że prawa strona równania (3.2) jest wielomianem trzeciego stopnia o miejscach zerowych ![]() ,
, ![]() ,
, ![]() — są to oczywiście stany stacjonarne naszego równania — i ujemnym współczynniku przy
— są to oczywiście stany stacjonarne naszego równania — i ujemnym współczynniku przy ![]() . Wobec tego
. Wobec tego
-
dla
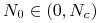 mamy
mamy 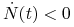 , czyli
, czyli 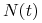 maleje do
maleje do 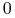 ;
; -
dla
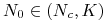 mamy
mamy 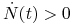 , czyli
, czyli 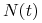 rośnie do
rośnie do 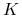 ;
; -
dla
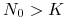 mamy
mamy 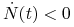 , czyli
, czyli 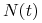 maleje do
maleje do 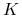 .
.
Policzymy też drugą pochodną, aby zbadać wklęsłość/wypukłość rozwiązań
Z kolei druga pochodna jest funkcją kwadratową zmiennej ![]() o wyróżniku
o wyróżniku
i pierwiastkach
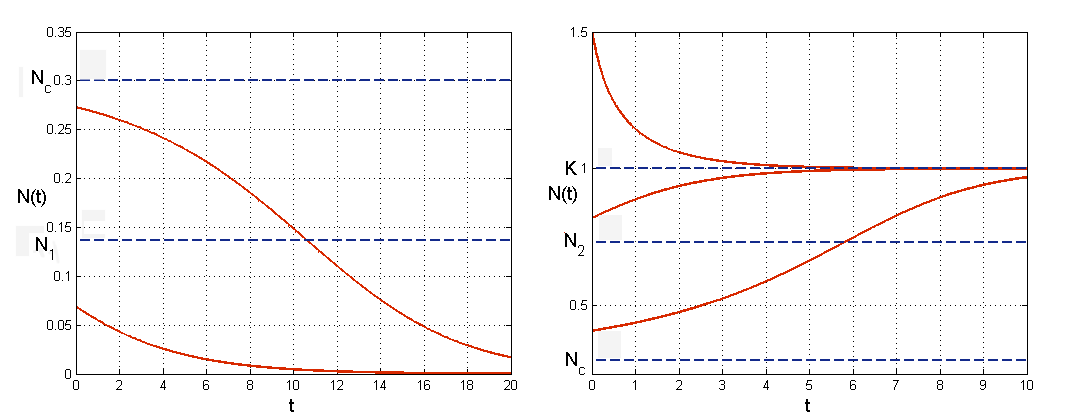
Ostatecznie, por. rys. 3.2,
-
dla
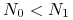 funkcja
funkcja 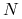 maleje i
maleje i 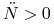 , czyli
, czyli 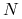 jest wypukła;
jest wypukła; -
dla
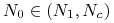 funkcja
funkcja 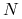 maleje i pozostaje wklęsła dopóki
maleje i pozostaje wklęsła dopóki 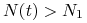 , w punkcie
, w punkcie 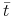 , takim że
, takim że 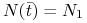 następuje zmiana charakteru przebiegu funkcji
następuje zmiana charakteru przebiegu funkcji 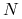 — staje się ona wypukła;
— staje się ona wypukła; -
dla
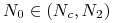 przebieg jest symetryczny względem stanu stacjonarnego
przebieg jest symetryczny względem stanu stacjonarnego 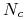 do opisanego w poprzednim punkcie (podobny do przebiegu krzywych logistycznych);
do opisanego w poprzednim punkcie (podobny do przebiegu krzywych logistycznych); -
dla
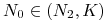 funkcja
funkcja 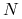 rośnie w sposób wklęsły do stanu stacjonarnego
rośnie w sposób wklęsły do stanu stacjonarnego 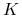 ;
;
-
dla
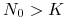 funkcja
funkcja 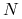 maleje w sposób wypukły.
maleje w sposób wypukły.
3.2. Funkcjonalna odpowiedź Hollinga i funkcja Hilla
W dalszym ciągu będziemy zajmować się sytuacją, w której na opisywaną populację ![]() ma wpływ drapieżnictwo. Wyprowadzimy wzór funkcji zwanej odpowiedzią funkcjonalną na obecność drapieżnika w oparciu o następujące rozumowanie zwane koncepcją dysku Hollinga [5]. Według tej koncepcji każdy drapieżnik polujący na danej powierzchni zauważa ofiary znajdujące się w obszarze o pewnym określonym promieniu
ma wpływ drapieżnictwo. Wyprowadzimy wzór funkcji zwanej odpowiedzią funkcjonalną na obecność drapieżnika w oparciu o następujące rozumowanie zwane koncepcją dysku Hollinga [5]. Według tej koncepcji każdy drapieżnik polujący na danej powierzchni zauważa ofiary znajdujące się w obszarze o pewnym określonym promieniu ![]() i promień ten jest charakterystyczny dla konkretnego gatunku drapieżnika. Spośród dostrzeżonych ofiar drapieżnik może upolować i zjeść pewną część. Zakładamy, że jest ona stała i oznaczamy tę część przez
i promień ten jest charakterystyczny dla konkretnego gatunku drapieżnika. Spośród dostrzeżonych ofiar drapieżnik może upolować i zjeść pewną część. Zakładamy, że jest ona stała i oznaczamy tę część przez ![]() . Każdy drapieżnik dzieli swój czas na dwa typy aktywności: wyszukiwanie ofiary oraz polowanie i zjadanie ofiary. Szukając ofiar drapieżnik przemieszcza się z pewną ustaloną prędkością
. Każdy drapieżnik dzieli swój czas na dwa typy aktywności: wyszukiwanie ofiary oraz polowanie i zjadanie ofiary. Szukając ofiar drapieżnik przemieszcza się z pewną ustaloną prędkością ![]() , a polowanie i konsumpcja jednej ofiary zajmują mu średnio
, a polowanie i konsumpcja jednej ofiary zajmują mu średnio ![]() jednostek czasu.
jednostek czasu.
Przy tych założeniach oszacujemy, ile średnio ofiar z populacji o zagęszczeniu ![]() zjada w jednostce czasu pojedynczy drapieżnik. Dowolny przedział czasu długości
zjada w jednostce czasu pojedynczy drapieżnik. Dowolny przedział czasu długości ![]() dzielimy na wymienione wyżej dwa typy aktywności, a za pomocą
dzielimy na wymienione wyżej dwa typy aktywności, a za pomocą
![]() oznaczymy czas przeznaczony na wyszukiwanie ofiary. W czasie wyszukiwania drapieżnik poruszający się z prędkością
oznaczymy czas przeznaczony na wyszukiwanie ofiary. W czasie wyszukiwania drapieżnik poruszający się z prędkością ![]() obejmuje swoim zasięgiem powierzchnię
obejmuje swoim zasięgiem powierzchnię ![]() , gdyż
, gdyż ![]() to droga, którą przebywa drapieżnik, przy czym w każdym kroku rozglądając się widzi ofiary w odległości nie większej niż
to droga, którą przebywa drapieżnik, przy czym w każdym kroku rozglądając się widzi ofiary w odległości nie większej niż ![]() w prawo i lewo. Zatem w przedziale czasu o długości
w prawo i lewo. Zatem w przedziale czasu o długości ![]() drapieżnik chwyta i zjada
drapieżnik chwyta i zjada ![]() ofiar w czasie
ofiar w czasie ![]() . Cały przedział czasu
. Cały przedział czasu ![]() możemy więc zapisać jako
możemy więc zapisać jako
Jeśli przez ![]() oznaczymy funkcję odpowiedzi drapieżnika, czyli
oznaczymy funkcję odpowiedzi drapieżnika, czyli
to
i ostatecznie
| (3.3) |
gdzie ![]() i
i ![]() , a równanie (3.3) nazywamy równaniem dysku Hollinga.
, a równanie (3.3) nazywamy równaniem dysku Hollinga.
Zauważmy, że
czyli nawet jeśli ofiar jest bardzo dużo, to drapieżnik nie może zjeść więcej niż pewną ich liczbę, określoną przez czas poświęcany na upolowanie i zjedzenie jednej ofiary. Jeśli rozpatrzymy skrajny przypadek, w którym ![]() przy ustalonej liczebności populacji ofiar, to
przy ustalonej liczebności populacji ofiar, to
co oznacza, że w takim przypadku możemy odpowiedź funkcjonalną modelować za pomocą składnika liniowego. Taką postać odpowiedzi funkcjonalnej nazywamy odpowiedzią Hollinga I typu, która charakteryzuje się brakiem ograniczenia względem liczebności populacji ofiar,
natomiast przy ![]() mamy odpowiedź typu II, która jest ograniczona.
mamy odpowiedź typu II, która jest ograniczona.
Wróćmy teraz do opisu dynamiki populacji ![]() . Załóżmy, że na jej liczebność wpływa drapieżnictwo, odpowiedź funkcjonalną opisuje funkcja (3.3) i możemy przyjąć stałą liczebność drapieżników
. Załóżmy, że na jej liczebność wpływa drapieżnictwo, odpowiedź funkcjonalną opisuje funkcja (3.3) i możemy przyjąć stałą liczebność drapieżników ![]() . Jeśli wewnętrzną dynamikę (bez uwzględnienia drapieżnictwa) populacji
. Jeśli wewnętrzną dynamikę (bez uwzględnienia drapieżnictwa) populacji ![]() opisuje równanie logistyczne (2.2), to ostatecznie zmiana liczebności podlega równaniu
opisuje równanie logistyczne (2.2), to ostatecznie zmiana liczebności podlega równaniu
| (3.4) |
gdzie ![]() oznacza maksymalne drapieżnictwo i
oznacza maksymalne drapieżnictwo i ![]() odpowiada takiej liczebności populacji, przy której drapieżnictwo jest równe połowie maksymalnej wielkości
odpowiada takiej liczebności populacji, przy której drapieżnictwo jest równe połowie maksymalnej wielkości ![]() (maksymalną wielkość osiąga się asymptotycznie, przy
(maksymalną wielkość osiąga się asymptotycznie, przy ![]() ).
).
Postać równania (3.4) nie daje gwarancji znalezienia rozwiązania analitycznego, ale metody portretu fazowego i badania wklęsłości/wypukłości rozwiązań omówione w kontekście poprzednich modeli mogą być zastosowane z powodzeniem także w tym przypadku. Przeanalizowanie dynamiki modelu (3.4) pozostawiamy jako ćwiczenie.
Wyprowadzona powyżej postać odpowiedzi funkcjonalnej (3.3) stanowi szczególny przypadek funkcji Hilla
| (3.5) |
przy czym stałą ![]() nazywamy współczynnikiem Hilla i w ogólnym przypadku nie musi to być liczba naturalna.
nazywamy współczynnikiem Hilla i w ogólnym przypadku nie musi to być liczba naturalna.
Widzimy, że dla ![]() funkcja Hilla odpowiada funkcjonalnej odpowiedzi Hollinga typu II. Funkcja Hilla została zaproponowana do opisu reakcji biochemicznych i w tym przypadku odzwierciedla ona szybkość reakcji. W szczególności
funkcja Hilla odpowiada funkcjonalnej odpowiedzi Hollinga typu II. Funkcja Hilla została zaproponowana do opisu reakcji biochemicznych i w tym przypadku odzwierciedla ona szybkość reakcji. W szczególności ![]() opisuje przypadek, gdy w reakcji biorą udział bimery (cząsteczki powstałe z połączenia dwóch pojedynczych monomerów). Zauważmy, że funkcja
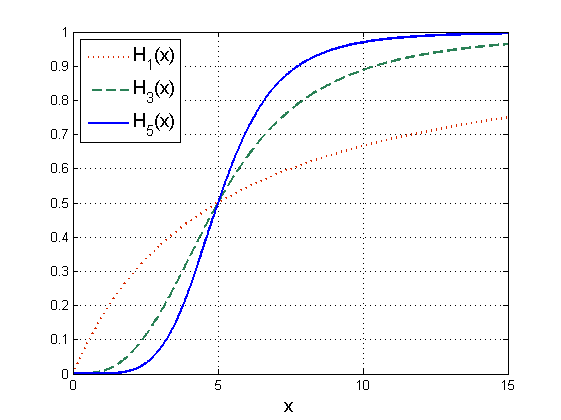
opisuje przypadek, gdy w reakcji biorą udział bimery (cząsteczki powstałe z połączenia dwóch pojedynczych monomerów). Zauważmy, że funkcja ![]() opisuje reakcje, które ulegają wysyceniu, przy czym w zależności od współczynnika
opisuje reakcje, które ulegają wysyceniu, przy czym w zależności od współczynnika ![]() mają różne tempo przebiegu reakcji dla
mają różne tempo przebiegu reakcji dla ![]() blisko
blisko ![]() i dla dużych
i dla dużych ![]() . Im większe
. Im większe ![]() , tym szybsze są zmiany w otoczeniu punktu krytycznego
, tym szybsze są zmiany w otoczeniu punktu krytycznego ![]() (będącego punktem przegięcia
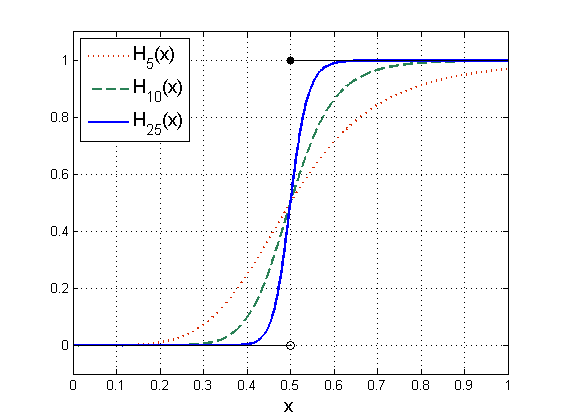
(będącego punktem przegięcia ![]() ). Funkcje Hilla możemy także interpretować jako gładkie przybliżenie tzw. funkcji przełączeniowych
). Funkcje Hilla możemy także interpretować jako gładkie przybliżenie tzw. funkcji przełączeniowych
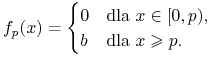 |
Funkcje Hilla są bardzo często wykorzystywane do opisu różnych procesów ulegających wysyceniu — wielkość współczynnika Hilla zależy wtedy od szybkości zmian danego procesu.