1. Modelowanie pojedynczej populacji I
W pierwszej części wykładu przedstawimy podstawowe modele opisujące ekosystem, w którym występuje tylko jedna populacja i opiszemy dynamikę takiej populacji w zależności od przyjętego modelu heurystycznego i formalizmu matematycznego.
1.1. Model Malthusa
W najprostszym przypadku zakładamy, że opisywana populacja ma w danym siedlisku bardzo dobre warunki rozwoju, wyrażające się głównie w taki sposób, że każdy osobnik ma nieograniczony dostęp do pożywienia i miejsc lęgowych oraz że
obserwujemy jedynie proces rozmnażania. Aby opis był możliwie najprostszy, osobniki w danej populacji powinny być jednakowe i podlegać jednakowym prawom. Co więcej, powinny być równomiernie rozłożone w przestrzeni, żeby nie wystąpiła konieczność analizowania zależności od przestrzeni, a tylko od czasu.
Przyjmujemy zatem następujący opis heurystyczny dla populacji ![]()
-
populacja jest jednorodna, składa się z genetycznie identycznych osobników rozmnażających się partenogenetycznie;
-
osobnik rodzi się w pełni ukształtowany, zdolny do rozrodu i może rozmnażać się w dowolnym wieku;
-
momenty rozmnażania są w dowolnym przedziale czasu rozłożone jednostajnie;
-
każdy osobnik wydaje na świat potomstwo co
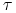 jednostek czasu,
jednostek czasu, 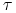 jest ustalone i jednakowe dla wszystkich osobników;
jest ustalone i jednakowe dla wszystkich osobników; -
każdorazowo jeden rodzic ma
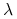 osobników potomnych.
osobników potomnych.
Na podstawie powyższych informacji spróbujemy zaproponować równanie opisujące średnią liczebność populacji ![]() w chwili
w chwili ![]() . Dokładniej, załóżmy że znamy liczebność w pewnej ustalonej chwili
. Dokładniej, załóżmy że znamy liczebność w pewnej ustalonej chwili ![]() i chcemy obliczyć
i chcemy obliczyć ![]() po upływie czasu
po upływie czasu ![]() . Zauważmy, że w przedziale czasu
. Zauważmy, że w przedziale czasu ![]() jest
jest
momentów rozmnażania. Każdy rodzic ma w tym przedziale czasu średnio
potomków. Liczba osobników zdolnych do rozmnażania w chwili ![]() wynosi
wynosi ![]() , zatem przyrost liczebności w krótkim przedziale czasu
, zatem przyrost liczebności w krótkim przedziale czasu ![]() możemy przybliżyć równaniem
możemy przybliżyć równaniem
| (1.1) |
Dzieląc stronami przez ![]() i przechodząc do granicy otrzymujemy
i przechodząc do granicy otrzymujemy
Przyjmijmy oznaczenia ![]() ,
, ![]() i przepiszmy powyższe równanie w postaci
i przepiszmy powyższe równanie w postaci
| (1.2) |
gdzie ![]() nazwiemy współczynnikiem rozrodczości populacji
nazwiemy współczynnikiem rozrodczości populacji ![]() . Zbudowaliśmy w ten sposób model ciągły (tzn. zmienna czasowa
. Zbudowaliśmy w ten sposób model ciągły (tzn. zmienna czasowa ![]() zmienia się w sposób ciągły i model heurystyczny jest opisany za pomocą równania różniczkowego).
Jeśli natomiast założymy, że
zmienia się w sposób ciągły i model heurystyczny jest opisany za pomocą równania różniczkowego).
Jeśli natomiast założymy, że ![]() , gdzie
, gdzie ![]() oznacza ustaloną jednostkę czasu i zastosujemy oznaczenie
oznacza ustaloną jednostkę czasu i zastosujemy oznaczenie ![]() , to równanie (1.1) możemy zapisać jako
, to równanie (1.1) możemy zapisać jako
| (1.3) |
otrzymujemy więc model dyskretny (zmienna czasowa zmienia się w sposób dyskretny, najczęściej ![]() , a liczebność populacji opisana jest za pomocą równania rekurencyjnego).
, a liczebność populacji opisana jest za pomocą równania rekurencyjnego).
Obydwa równania (1.2) i (1.3) nazywamy modelem Malthusa, odpowiednio w wersji ciągłej i dyskretnej. Thomas Malthus, angielski ekonomista i demograf, pod koniec XVIII wieku zwrócił uwagę na zbyt szybki przyrost liczebności populacji ludzkiej.
W pracy zatytułowanej ,,An Essay on the Principle of Population” sformułował swoje słynne prawo, które mówi, że liczba ludności wzrasta w tempie geometrycznym, natomiast zasoby żywności w tempie arytmetycznym, co w oczywisty sposób musi doprowadzić do katastrofy. Zauważmy, że równanie dyskretne (1.3) w bezpośredni sposób odzwierciedla fragment prawa Malthusa odnoszący się do liczebności populacji ludzkiej, natomiast równanie (1.2) jest jego ciągłym odpowiednikiem.
Każde z równań (1.2) i (1.3) możemy w prosty sposób rozwiązać, korzystając z ich liniowości. Przypomnijmy, że dla układów liniowych równań różniczkowych poszukujemy rozwiązań bazowych w postaci wykładniczej
a dla równań różnicowych — w postaci potęgowej
przy czym stałą ![]() nazywamy wartością własną.
Oczywiście w przypadku jednej zmiennej
równanie (1.2) rozwiązujemy wprost jako równanie o zmiennych rozdzielonych
nazywamy wartością własną.
Oczywiście w przypadku jednej zmiennej
równanie (1.2) rozwiązujemy wprost jako równanie o zmiennych rozdzielonych
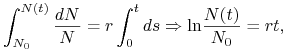 |
czyli ![]() . Natomiast równanie (1.3) opisuje ciąg geometryczny o ilorazie
. Natomiast równanie (1.3) opisuje ciąg geometryczny o ilorazie ![]() , którego poszczególne wyrazy obliczamy ze wzoru ogólnego
, którego poszczególne wyrazy obliczamy ze wzoru ogólnego
co można łatwo udowodnić stosując zasadę indukcji matematycznej.
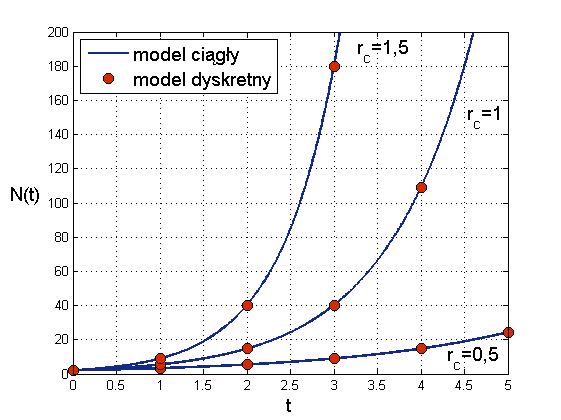
Jakie są własności rozwiązań obu wersji modelu Malthusa? Widzimy, że zarówno funkcja ![]() jak i ciąg geometryczny
jak i ciąg geometryczny ![]() ,
, ![]() , są rosnące nieograniczenie, por. rys. 1.1. Co więcej, dla ustalonego
, są rosnące nieograniczenie, por. rys. 1.1. Co więcej, dla ustalonego ![]() , jeśli współczynnik rozrodczości w modelu ciągłym oznaczymy przez
, jeśli współczynnik rozrodczości w modelu ciągłym oznaczymy przez ![]() , a w dyskretnym —
, a w dyskretnym — ![]() , to możemy dobrać
, to możemy dobrać ![]() do
do ![]() (albo odwrotnie), tak by rozwiązania dla
(albo odwrotnie), tak by rozwiązania dla ![]() pokrywały się. Mianowicie, chcemy mieć
pokrywały się. Mianowicie, chcemy mieć
więc ![]() , czyli
, czyli ![]() , przy czym oczywiście
, przy czym oczywiście ![]() .
.
Z dynamiki modeli (1.2) i (1.3) wynika jasno, że mogą one mieć tylko ograniczony zakres stosowalności. Jedynie hipotetyczna populacja może rozrastać się nieograniczenie, natomiast w rzeczywistości zawsze działają różne mechanizmy ograniczające taki przyrost, w szczególności pojemność siedliska, w którym występuje populacja ![]() jest zawsze ograniczona i zbyt duża liczba osobników w tym siedlisku się nie zmieści.
Pokreślić należy, już sam Malthus zwrócił uwagę na fakt, że ilość żywności przyrasta znacznie wolniej niż liczba ludności, co w konsekwencji musi prowadzić do konkurencji o pożywienie.
Zawsze także obok procesu rozrodczości występuje proces śmiertelności.
jest zawsze ograniczona i zbyt duża liczba osobników w tym siedlisku się nie zmieści.
Pokreślić należy, już sam Malthus zwrócił uwagę na fakt, że ilość żywności przyrasta znacznie wolniej niż liczba ludności, co w konsekwencji musi prowadzić do konkurencji o pożywienie.
Zawsze także obok procesu rozrodczości występuje proces śmiertelności.
1.2. Procesy rozrodczości i śmiertelności
Ponieważ uświadomiliśmy sobie, że w naszym modelu dynamiki populacji musimy uwzględnić nie tylko rozrodczość, ale także i inne procesy, w szczególności śmiertelność osobników danej populacji, a chcemy to ponownie zrobić w jak najprostszy sposób, to odpowiedni model heurystyczny budujemy analogicznie jak w przypadku procesu rozrodczości, przyjmując takie same założenia o jednorodności populacji. Wobec tego zamiast równania (1.1) dostaniemy w rezultacie
gdzie ![]() nazywamy współczynnikiem śmiertelności. Odzwierciedla on procent osobników umierających w jednostce czasu. Zauważmy, że
nazywamy współczynnikiem śmiertelności. Odzwierciedla on procent osobników umierających w jednostce czasu. Zauważmy, że ![]() możemy interpretować jako średnią długość życia pojedynczego osobnika.
możemy interpretować jako średnią długość życia pojedynczego osobnika.
Ostatecznie z analitycznego punktu widzenia, po uwzględnieniu procesu śmiertelności w modelu Malthusa dostajemy taką samą strukturę matematyczną jak poprzednio. Oznaczmy przez ![]() współczynnik rozrodczości ,,netto”, czyli różnicę między współczynnikiem rozrodczości a śmiertelności. Często
współczynnik rozrodczości ,,netto”, czyli różnicę między współczynnikiem rozrodczości a śmiertelności. Często ![]() nazywamy współczynnikiem reprodukcji lub współczynnikiem przyrostu naturalnego. Wtedy mamy
nazywamy współczynnikiem reprodukcji lub współczynnikiem przyrostu naturalnego. Wtedy mamy
| (1.4) |
w modelu ciągłym oraz
| (1.5) |
w modelu dyskretnym.
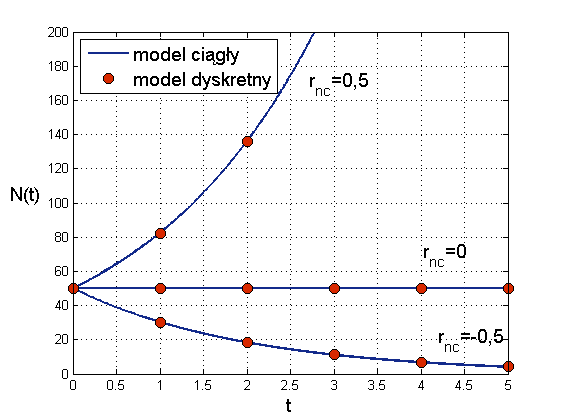
Widzimy, że jeśli przyrost naturalny jest dodatni, ![]() , to liczebność populacji rośnie, choć oczywiście nieco wolniej niż dla
, to liczebność populacji rośnie, choć oczywiście nieco wolniej niż dla ![]() . Natomiast gdy
. Natomiast gdy ![]() , to charakter rozwiązań obu modeli zmienia się. W modelu ciągłym mamy
, to charakter rozwiązań obu modeli zmienia się. W modelu ciągłym mamy
zatem liczebność populacji spada. Rozwiązaniem jest funkcja wykładnicza o ujemnym wykładniku, czyli
wobec tego asymptotycznie populacja wymiera. Analogicznie w modelu dyskretnym mamy ciąg geometryczny o ilorazie mniejszym niż ![]() , czyli także
, czyli także ![]() maleje do zera przy
maleje do zera przy ![]() , por. rys. 1.2.
, por. rys. 1.2.
1.3. Migracje
Kolejnym krokiem przybliżającym nasz model do rzeczywistości może być uwzględnienie emigracji osobników w związku z ograniczoną pojemnością siedliska. W najprostszych modelach zakłada się dwa typy migracji
-
migracja stała w czasie;
-
migracja zależna od zagęszczenia.
Zauważmy, że przy drugim typie migracji w równaniu (1.4) ponownie musimy uwzględnić składnik ![]() , gdzie
, gdzie ![]() oznacza frakcję osobników migrujących przypadających na jednostkę czasu, zatem
oznacza frakcję osobników migrujących przypadających na jednostkę czasu, zatem
i taki sposób migracji nie wpływa na ogólną postać rozwiązań modelu — rozwiązaniem jest zawsze funkcja wykładnicza, przy czym jeśli emigracja nie jest zbyt duża, czyli ![]() , to populacja w dalszym ciągu rośnie nieograniczenie, jeśli przyrost naturalny jest dodatni, natomiast zbyt duża emigracja
, to populacja w dalszym ciągu rośnie nieograniczenie, jeśli przyrost naturalny jest dodatni, natomiast zbyt duża emigracja ![]() spowoduje, że siedlisko zostanie opuszczone, ale matematycznie realizuje się to w nieskończonym czasie. Wobec tego dynamika nie różni się od modelu rozrodczości/śmiertelności omawianego poprzednio. Tak samo przedstawia się dynamika wersji dyskretnej.
spowoduje, że siedlisko zostanie opuszczone, ale matematycznie realizuje się to w nieskończonym czasie. Wobec tego dynamika nie różni się od modelu rozrodczości/śmiertelności omawianego poprzednio. Tak samo przedstawia się dynamika wersji dyskretnej.
Zastanówmy się wobec tego jak zmieni się model, jeśli założymy, że emigracja jest stała w czasie i nie zależy od zagęszczenia populacji. Wtedy współczynnik emigracji ![]() odzwierciedla liczbę osobników, które emigrują (zatem ubywa osobników w siedlisku) w jednostce czasu (na jednostkę powierzchni, ponieważ opisujemy zagęszczenie). Zamiast równania (1.4) otrzymamy
odzwierciedla liczbę osobników, które emigrują (zatem ubywa osobników w siedlisku) w jednostce czasu (na jednostkę powierzchni, ponieważ opisujemy zagęszczenie). Zamiast równania (1.4) otrzymamy
| (1.6) |
Zwróćmy uwagę, że z matematycznego punktu widzenia możemy rozważać różne układy znaków parametrów ![]() i
i ![]() w równaniu
w równaniu
| (1.7) |
odzwierciedlające odpowiednio
-
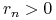 i
i 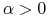 — dodatni przyrost naturalny i imigrację;
— dodatni przyrost naturalny i imigrację; -
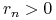 i
i 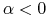 — dodatni przyrost naturalny i emigrację;
— dodatni przyrost naturalny i emigrację; -
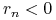 i
i 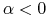 — ujemny przyrost naturalny i emigrację;
— ujemny przyrost naturalny i emigrację; -
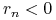 i
i 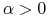 — ujemny przyrost naturalny i imigrację.
— ujemny przyrost naturalny i imigrację.
Model (1.7) możemy także interpretować w inny sposób. Współczynnik ![]() oznacza wprowadzanie (introdukcję) nowych osobników do siedliska, natomiast
oznacza wprowadzanie (introdukcję) nowych osobników do siedliska, natomiast ![]() oznacza odławianie osobników. Wyobraźmy sobie zatem staw z rybami i spróbujmy zinterpretować każdy przypadek. Najłatwiejsza wydaje się interpretacja drugiego przypadku — populacja ryb zwiększa się, więc je odławiamy. Przypadek pierwszy jest z tego punktu widzenia najbardziej problematyczny, ale zakładając niewielką wartość
oznacza odławianie osobników. Wyobraźmy sobie zatem staw z rybami i spróbujmy zinterpretować każdy przypadek. Najłatwiejsza wydaje się interpretacja drugiego przypadku — populacja ryb zwiększa się, więc je odławiamy. Przypadek pierwszy jest z tego punktu widzenia najbardziej problematyczny, ale zakładając niewielką wartość ![]() możemy
pewien czas możemy nie zauważać istotnego przyrostu, więc introdukcja w celu podtrzymania gatunku może wydawać się konieczna. Podobnie w trzecim przypadku — przy małym ujemnym przyroście naturalnym możemy przez pewien czas nie zauważać zmniejszania się populacji z tego powodu i eksploatować tę populację przez odłów (czasem zdarza się tak, że zauważamy ujemny przyrost naturalny, ale z różnych powodów w dalszym ciągu eksploatujemy populację). Przypadek czwarty oznacza oczywiście pozytywną ingerencję człowieka — ponieważ przyrost naturalny jest ujemny, więc zarybiamy staw, by utrzymać populację w siedlisku.
możemy
pewien czas możemy nie zauważać istotnego przyrostu, więc introdukcja w celu podtrzymania gatunku może wydawać się konieczna. Podobnie w trzecim przypadku — przy małym ujemnym przyroście naturalnym możemy przez pewien czas nie zauważać zmniejszania się populacji z tego powodu i eksploatować tę populację przez odłów (czasem zdarza się tak, że zauważamy ujemny przyrost naturalny, ale z różnych powodów w dalszym ciągu eksploatujemy populację). Przypadek czwarty oznacza oczywiście pozytywną ingerencję człowieka — ponieważ przyrost naturalny jest ujemny, więc zarybiamy staw, by utrzymać populację w siedlisku.
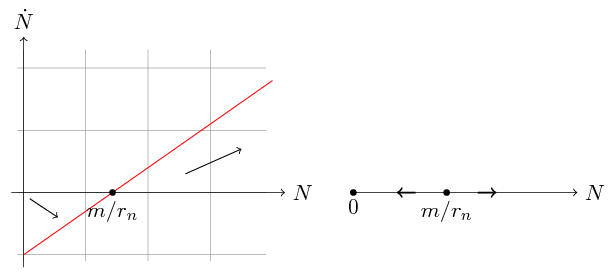
Z punktu widzenia interesującego nas teraz zagadnienia ograniczenia pojemności siedliska najważniejszy jest przypadek drugi, zatem przeprowadzimy jego analizę, a pozostałe trzy należy potraktować jako ćwiczenie. Zajmiemy się więc teraz równaniem (1.6) z dodatnimi parametrami ![]() i
i ![]() . Narysujmy najpierw zależność
. Narysujmy najpierw zależność ![]() w przestrzeni
w przestrzeni ![]() , gdzie
, gdzie ![]() oznacza liczby rzeczywiste nieujemne, por. rys. 1.4.
oznacza liczby rzeczywiste nieujemne, por. rys. 1.4.
Zauważmy, że pochodna ![]() jest dla
jest dla ![]() ujemna, co oznacza, że liczebność maleje, natomiast dla
ujemna, co oznacza, że liczebność maleje, natomiast dla ![]() mamy
mamy ![]() , czyli liczebność rośnie. Jakie wnioski możemy wysnuć z tej prostej analizy? Musimy zacząć od przypomnienia sobie podstawowych własności rozwiązań równań różniczkowych zwyczajnych (RRZ). W naszym przypadku prawa strona równania (1.6) jest funkcją klasy
, czyli liczebność rośnie. Jakie wnioski możemy wysnuć z tej prostej analizy? Musimy zacząć od przypomnienia sobie podstawowych własności rozwiązań równań różniczkowych zwyczajnych (RRZ). W naszym przypadku prawa strona równania (1.6) jest funkcją klasy ![]() (nawet analityczną), więc rozwiązania tego równania są jednoznaczne.
Co więcej, ponieważ równanie (1.6) jest liniowe, więc dla dowolnego
(nawet analityczną), więc rozwiązania tego równania są jednoznaczne.
Co więcej, ponieważ równanie (1.6) jest liniowe, więc dla dowolnego ![]() (tylko taki warunek początkowy ma sens biologiczny, z analitycznego punktu widzenia możemy rozpatrywać dowolne
(tylko taki warunek początkowy ma sens biologiczny, z analitycznego punktu widzenia możemy rozpatrywać dowolne ![]() ) rozwiązanie istnieje dla wszystkich
) rozwiązanie istnieje dla wszystkich ![]() , choć zwykle interesuje nas przewidywanie dynamiki populacji w przyszłości, więc ograniczamy się do
, choć zwykle interesuje nas przewidywanie dynamiki populacji w przyszłości, więc ograniczamy się do ![]() .
Zauważmy dalej, że
.
Zauważmy dalej, że ![]() jest rozwiązaniem stacjonarnym, czyli jeśli
jest rozwiązaniem stacjonarnym, czyli jeśli ![]() , to
, to ![]() dla dowolnego
dla dowolnego ![]() , co oznacza, że rozwiązanie nie zmienia się w czasie. Jest to jedyne rozwiązanie stacjonarne.
Stąd jeśli
, co oznacza, że rozwiązanie nie zmienia się w czasie. Jest to jedyne rozwiązanie stacjonarne.
Stąd jeśli ![]() , to liczebność populacji maleje i nie ma żadnej ,,bariery”, która mogłaby ten spadek zahamować. Z teorii RRZ wynika, że taką barierę może stanowić tylko rozwiązanie stacjonarne.
Faktycznie — załóżmy, że
, to liczebność populacji maleje i nie ma żadnej ,,bariery”, która mogłaby ten spadek zahamować. Z teorii RRZ wynika, że taką barierę może stanowić tylko rozwiązanie stacjonarne.
Faktycznie — załóżmy, że ![]() przy
przy ![]() . Wtedy
. Wtedy ![]() . Ponieważ
. Ponieważ ![]() , to od pewnego momentu
, to od pewnego momentu ![]() zachodzi
zachodzi ![]() z czego wynika, że
z czego wynika, że ![]() , a to implikuje, że
, a to implikuje, że ![]() . Wobec tego nie może zachodzić nierówność
. Wobec tego nie może zachodzić nierówność ![]() . Wnioskujemy więc, że
. Wnioskujemy więc, że ![]() , zatem istnieje taki moment
, zatem istnieje taki moment ![]() , dla którego
, dla którego ![]() . Ze względu na liniowość równania (1.6) możemy je łatwo rozwiązać (jak poprzednio jest to równanie o zmiennych rozdzielonych lub też możemy skorzystać z metody uzmienniania stałej)
. Ze względu na liniowość równania (1.6) możemy je łatwo rozwiązać (jak poprzednio jest to równanie o zmiennych rozdzielonych lub też możemy skorzystać z metody uzmienniania stałej)
Analityczna postać rozwiązania tylko potwierdza wcześniejsze wnioski płynące z zależności ![]() . Zauważmy dalej, że obliczając drugą pochodną dostajemy
. Zauważmy dalej, że obliczając drugą pochodną dostajemy
zatem jeśli funkcja ![]() jest rosnąca, to rośnie w sposób wypukły (jest to w zasadzie wzrost wykładniczy), natomiast gdy jest malejąca — jest także wklęsła, co oczywiście oznacza, że w skończonym czasie
jest rosnąca, to rośnie w sposób wypukły (jest to w zasadzie wzrost wykładniczy), natomiast gdy jest malejąca — jest także wklęsła, co oczywiście oznacza, że w skończonym czasie ![]() przekracza oś poziomą (co już wcześniej zauważyliśmy).
Znając postać rozwiązania możemy wyznaczyć
przekracza oś poziomą (co już wcześniej zauważyliśmy).
Znając postać rozwiązania możemy wyznaczyć ![]() jako taki czas, dla którego liczebność populacji zeruje się. Skoro
jako taki czas, dla którego liczebność populacji zeruje się. Skoro ![]() , to
, to
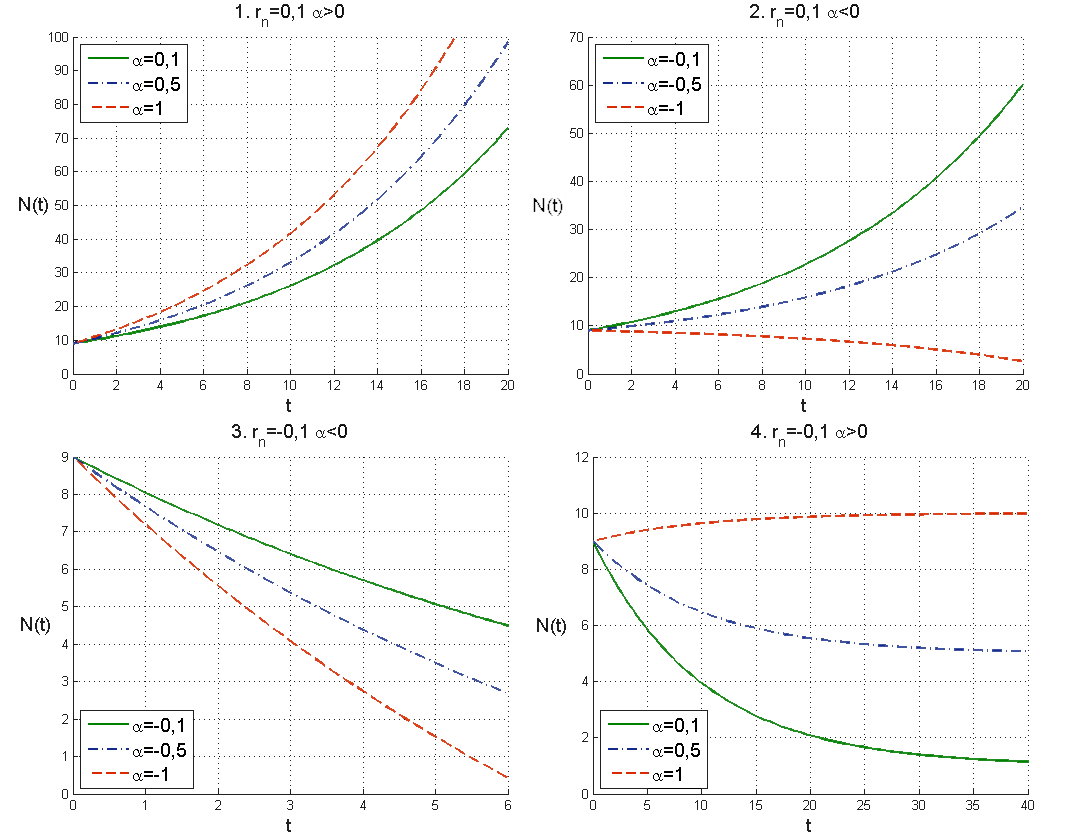
Przykładowe rozwiązania tego modelu zostały przedstawione na prawym górnym wykresie na rys. 1.3. Widzimy, że w zależności od wielkości emigracji populacja albo rośnie nieograniczenie, jak w przypadku bazowego modelu Malthusa, albo wymiera w skończonym czasie, jeśli zbyt dużo osobników emigruje. Pozostałe przypadki migracji analizujemy w analogiczny sposób, pozostawiamy tę analizę i płynące z niej wnioski jako ćwiczenie.