Zagadnienia
12. Modelowanie odpowiedzi odpornościowej
Dwa kolejne wykłady zostaną poświęcone modelowaniu reakcji odpornościowych. Na początku przedstawimy podstawowe informacje dotyczące działania układu odpornościowego człowieka.
12.1. Układ odpornościowy człowieka
Układ odpornościowy człowieka (i nie tylko człowieka) jest bardzo skomplikowany. Odpowiedź odpornościową wywołuje antygen. Antygenem nazywamy substancję, która wykazuje się:
-
immunogennością, czyli zdolnością indukowania swoistej (specyficznej) odpowiedzi odpornościowej przeciw sobie;
-
antygenowością, czyli zdolnością do swoistego łączenia się z immunoglobulinami (zarówno wolnymi jak i stanowiącymi receptory limfocytów $B$) oraz receptorami limfocytów $T$.
Okazuje się, że w obrębie jednego antygenu może znajdować się wiele miejsc wiązanych przez przeciwciała. Są to tzw. epitopy lub determinanty antygenowe. Epitopy obecne w jednej cząsteczce antygenu mogą być identyczne lub różne i mogą być wiązane przez przeciwciała o tej samej lub różnej swoistości. Antygen zawierający wiele epitopów nazywamy wielowartościowym lub poliwalentnym.
Reakcja odpornościowa składa się z wielu różnorodnych procesów, w których bierze udział wiele składników układu odpornościowego. Najważniejsze z tych składników to:
-
wśród komórek odpornościowych:
-
limfocyty
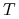 ;
; -
limfocyty
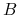 ;
; -
komórki prezentujące antygen, ang. antigen presenting cells (APC);
-
wśród cząstek:
-
immunoglobuliny (przeciwciała);
-
receptory limfocytów wiążące się z antygenem.
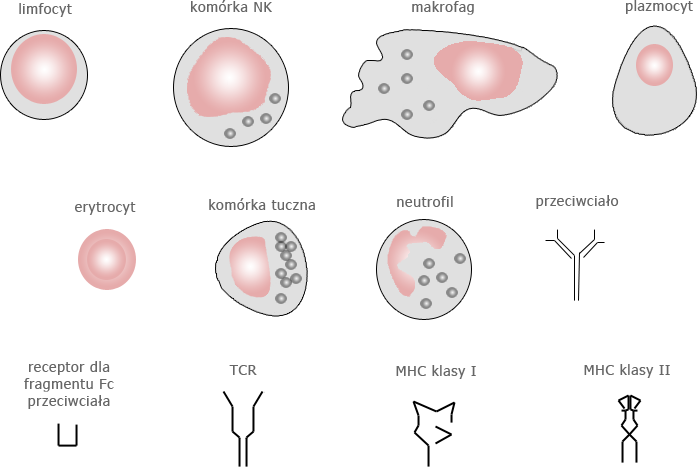
Zestawienie najważniejszych składników układu odpornościowego przedstawiamy na rys. 12.1 i w tabeli 12.1.
| Limfocyty |
rozpoznają antygeny i wytwarzają przeciwciała |
|---|---|
| Komórki plazmatyczne (plazmocyty) | wytwarzają przeciwciała |
| Limfocyty |
wspomagają odpowiedź odpornościową; wydzielają cytokiny |
| Limfocyty |
hamują odpowiedź odpornościową; wydzielają cytokiny |
| Limfocyty |
są zdolne do zabijania komórek docelowych |
| Komórki |
są zdolne do cytotoksyczności komórkowej zależnej od przeciwciał |
| Komórki |
są zdolne do spontanicznego zabijania komórek nowotworowych i zakażonych przez wirusy |
| Komórki dendrytyczne | prezentują antygeny limfocytom |
| Monocyty, makrofagi | są zdolne do fagocytozy i zabicia mikroorganizmów oraz innych obcych komórek; wydzielają cytokiny |
| Neutrofile | są zdolne do fagocytozy i zabijania mikroorganizmów |
| Komórki tuczne, bazofile | biorą udział w nadwrażliwości I (anafilaksji) |
| Eozynofile | są zdolne do fagocytozy i zbijania niektórych pasożytów z użyciem przeciwciał |
| Megakariocyty | wytwarzają trombocyty, które uczestniczą w krzepnięciu krwi i reakcjach zapalnych |
| Erytrocyty | poprzez receptor dla dopełniacza wiążą kompleksy immunologiczne i uczestniczą w ich usuwaniu |
W każdej odpowiedzi odpornościowej oprócz komórek efektorowych (np. limfocytów ![]() wytwarzających przeciwciała lub cytotoksycznych limfocytów
wytwarzających przeciwciała lub cytotoksycznych limfocytów ![]() ) uczestniczą także komórki regulujące tę odpowiedź.
) uczestniczą także komórki regulujące tę odpowiedź.
Rodzinę komórek zwanych limfocytami ![]() dzielimy na kilka grup, w zależności od spełnianych przez nie funkcji:
dzielimy na kilka grup, w zależności od spełnianych przez nie funkcji:
-
limfocyty $T$ cytotoksyczne (
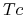 ), które są zdolne do zabicia innych komórek, takich jak komórki obce, komórki nowotworowe, komórki zainfekowane przez wirusy;
), które są zdolne do zabicia innych komórek, takich jak komórki obce, komórki nowotworowe, komórki zainfekowane przez wirusy; -
limfocyty $T$ pomocnicze, ang.
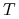 helper cells (
helper cells (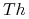 ), które wspomagają odpowiedź odpornościową;
), które wspomagają odpowiedź odpornościową; -
limfocyty $T$ regulatorowe, ang. regulatory
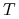 cells (
cells (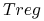 ),
które hamują odpowiedź odpornościową.
),
które hamują odpowiedź odpornościową.
Z kolei limfocyty ![]() należą do klasy komórek prezentujących antygen APC i uczestniczą w procesie rozpoznawania antygenu i przygotowywania swoistej odpowiedzi odpornościowej przeciw temu antygenowi. Następnie w procesie różnicowania stają się komórkami plazmatycznymi, które produkują przeciwciała zwalczające dany antygen.
należą do klasy komórek prezentujących antygen APC i uczestniczą w procesie rozpoznawania antygenu i przygotowywania swoistej odpowiedzi odpornościowej przeciw temu antygenowi. Następnie w procesie różnicowania stają się komórkami plazmatycznymi, które produkują przeciwciała zwalczające dany antygen.
Typy odpowiedzi odpornościowej
Odpowiedź odpornościową możemy podzielić na:
-
swoistą (specyficzną) i nieswoistą (niespecyficzną);
-
typu humoralnego i komórkowego.
Mechanizmy nieswoiste nazywane są też odpornością natywną lub wrodzoną. Jednak żadna z tych nazw nie oddaje istoty tego typu reakcji. Podobnie zresztą dzieje się w przypadku mechanizmów swoistych nazywanych też odpornością adoptywną.
Mechanizmy nieswoiste rozwinęły się wcześniej w filogenezie (tzn. są starsze ewolucyjnie), są mniej precyzyjne, ale reakcje zachodzą szybko. Mówi się, że stanowią pierwszą linię obrony organizmu. Z kolei mechanizmy swoiste są filogenetycznie młodsze. W trakcie reakcji odpornościowej pojawienie się tych mechanizmów wymaga czasu, ale nakierowane są dokładnie przeciw konkretnemu rodzajowi antygenu, więc działają precyzyjniej i skuteczniej.
W odpowiedzi swoistej biorą udział głównie antygeny swoiste wyprodukowane przez komórki plazmatyczne powstałe w procesie rozpoznawania antygenu przez limfocyty ![]() oraz limfocyty
oraz limfocyty ![]() ze swoistymi receptorami wiążącymi konkretny antygen.
ze swoistymi receptorami wiążącymi konkretny antygen.
Z kolei podział na odpowiedź humoralną i komórkową jest cokolwiek sztuczny. W większości przypadków obserwuje się oba typy reakcji, chociaż w konkretnych przypadkach dla danego antygenu jedna z nich może dominować nad drugą.
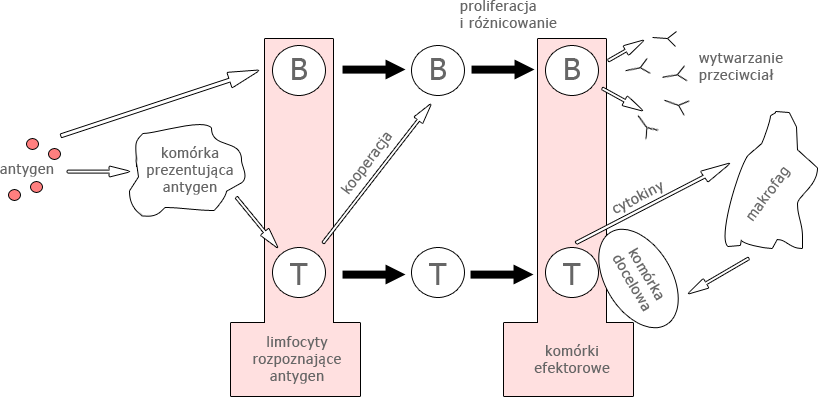
W odpowiedzi humoralnej decydującą rolę w zwalczaniu antygenu odgrywają przeciwciała obecne głównie we krwi odwodowej i limfie, ale także w innych płynach organicznych, natomiast za odpowiedź komórkową odpowiadają limfocyty ![]() , por. rys. 12.2. Limfocyty cytotoksyczne
, por. rys. 12.2. Limfocyty cytotoksyczne ![]() bezpośrednio zwalczają antygen za pomocą swoistych receptorów, natomiast limfocyty pomocnicze Th w reakcji ze swoistym antygenem wydzielają cytokiny, które aktywują makrofagi i granulocyty niszczące antygen.
bezpośrednio zwalczają antygen za pomocą swoistych receptorów, natomiast limfocyty pomocnicze Th w reakcji ze swoistym antygenem wydzielają cytokiny, które aktywują makrofagi i granulocyty niszczące antygen.
12.2. Proste modele odpowiedzi odpornościowej
Zajmiemy się teraz zaproponowaniem możliwie najprostszych modeli odpowiedzi odpornościowej, gdzie ponownie wykorzystamy znane już sposoby modelowania oddziaływań między różnymi populacjami. Zacznijmy od opisu wewnętrznej dynamiki antygenu. Pod względem tejże dynamiki możemy antygeny podzielić na:
-
aktywne, jak bakterie, grzyby i wirusy, mające zdolność aktywnego namnażania się w organizmie;
-
pasywne, jak trucizny i jady, które się nie namnażają;
-
własne, czyli produkowane przez organizm, jak autoantygeny czy antygeny transplantacyjne.
Niech ![]() oznacza zagęszczenie antygenu w organizmie w chwili
oznacza zagęszczenie antygenu w organizmie w chwili ![]() .
W najprostszym przypadku wewnętrzną dynamikę pierwszego typu antygenu możemy opisać równaniem
.
W najprostszym przypadku wewnętrzną dynamikę pierwszego typu antygenu możemy opisać równaniem
| (12.1) |
gdzie ![]() oznacza współczynnik namnażania netto (czyli różnicę między współczynnikiem rozrodczości i śmiertelności). Oczywiście tylko gdy
oznacza współczynnik namnażania netto (czyli różnicę między współczynnikiem rozrodczości i śmiertelności). Oczywiście tylko gdy ![]() antygen istotnie jest aktywny. Z kolei dla antygenu pasywnego możemy rozważać takie samo równanie wewnętrznej dynamiki przy założeniu
antygen istotnie jest aktywny. Z kolei dla antygenu pasywnego możemy rozważać takie samo równanie wewnętrznej dynamiki przy założeniu ![]() .
Natomiast trzeciemu typowi antygenu odpowiada w najprostszym przypadku równanie
.
Natomiast trzeciemu typowi antygenu odpowiada w najprostszym przypadku równanie
| (12.2) |
gdzie ![]() oznacza stałe źródło, a
oznacza stałe źródło, a ![]() — współczynnik śmiertelności, przy czym
— współczynnik śmiertelności, przy czym ![]() to średnia długość życia takiego antygenu.
to średnia długość życia takiego antygenu.
Zakładamy teraz, że dany antygen wywołuje odpowiedź odpornościową, którą w modelu reprezentują efektory (limfocyty lub przeciwciała) o zagęszczeniu ![]() . Wobec tego w równaniu (12.1) (odpowiednio (12.2)) musimy uwzględnić kolejny składnik opisujący oddziaływanie antygen – efektor.
Bazując na modelu drapieżnik – ofiara otrzymamy zamiast (12.1) równanie
. Wobec tego w równaniu (12.1) (odpowiednio (12.2)) musimy uwzględnić kolejny składnik opisujący oddziaływanie antygen – efektor.
Bazując na modelu drapieżnik – ofiara otrzymamy zamiast (12.1) równanie
gdzie ![]() odzwierciedla skuteczność efektorów w zwalczaniu antygenów.
odzwierciedla skuteczność efektorów w zwalczaniu antygenów.
Układ odpornościowy aktywuje się po wykryciu antygenu przez komórki odpornościowe. Wiemy też, że efektory zużywają się w trakcie odpowiedzi odpornościowej, zatem równanie ich dynamiki możemy zapisać w następującej postaci
gdzie ![]() oznacza współczynnik aktywacji, a
oznacza współczynnik aktywacji, a ![]() — śmiertelność efektorów w wyniku reakcji odpornościowej.
— śmiertelność efektorów w wyniku reakcji odpornościowej.
Ostatecznie model odpowiedzi odpornościowej przeciw antygenowi aktywnemu opiszemy następującym układem dwóch równań różniczkowych zwyczajnych
![\begin{array}[]{lcl}\dot{V}&=&\beta V-\gamma VE,\\
\dot{E}&=&\eta V-\nu VE,\end{array}](wyklady/mbm/mi/mi1141.png) |
(12.3) |
z dodatnimi współczynnikami. Analogicznie możemy modelować odpowiedź przeciwko antygenowi pasywnemu oraz autoantygenowi, co pozostawiamy jako ćwiczenie.
Przejdziemy teraz do analizy układu (12.3). Podstawowe własności jak istnienie, jednoznaczność, nieujemność i przedłużalność rozwiązań badamy w sposób standardowy. Istnienie i jednoznaczność rozwiązań dla dowolnego warunku początkowego ![]() wynika z gładkości prawej strony układu. Nieujemność pierwszej zmiennej dla nieujemnego warunku początkowego wynika z tego, że oś
wynika z gładkości prawej strony układu. Nieujemność pierwszej zmiennej dla nieujemnego warunku początkowego wynika z tego, że oś ![]() jest zbiorem niezmienniczym. W przypadku drugiej zmiennej
jest zbiorem niezmienniczym. W przypadku drugiej zmiennej ![]() , jeśli założymy, że istnieje
, jeśli założymy, że istnieje ![]() , dla którego
, dla którego ![]() , to otrzymamy
, to otrzymamy ![]() , zatem rozwiązanie nie może opuścić pierwszej ćwiartki układu współrzędnych. Nieujemność rozwiązań implikuje też ich przedłużalność dla wszystkich
, zatem rozwiązanie nie może opuścić pierwszej ćwiartki układu współrzędnych. Nieujemność rozwiązań implikuje też ich przedłużalność dla wszystkich ![]() , ponieważ prawa strona układu ma w tym przypadku oszacowanie liniowe — obie pochodne szacują się przez
, ponieważ prawa strona układu ma w tym przypadku oszacowanie liniowe — obie pochodne szacują się przez ![]() , gdzie odpowiednio
, gdzie odpowiednio ![]() dla zmiennej
dla zmiennej ![]() i
i ![]() dla
dla ![]() .
.
W kolejnym kroku analizy znajdziemy izokliny zerowe i naszkicujemy portrety fazowe w zależności od parametrów układu (12.3). Widzimy, że
![\begin{array}[]{ccc}\dot{V}=0&\Longleftrightarrow&V=0\ \ \text{lub}\ \ E=\frac{\beta}{\gamma},\\
\dot{E}=0&\Longleftrightarrow&V=0\ \ \text{lub}\ \ E=\frac{\eta}{\nu}.\\
\end{array}](wyklady/mbm/mi/mi1108.png) |
Zauważmy, że oś ![]() jest izokliną zarówno dla
jest izokliną zarówno dla ![]() jak i dla
jak i dla ![]() . Mamy więc do czynienia z przypadkiem niehiperbolicznym. Cała oś
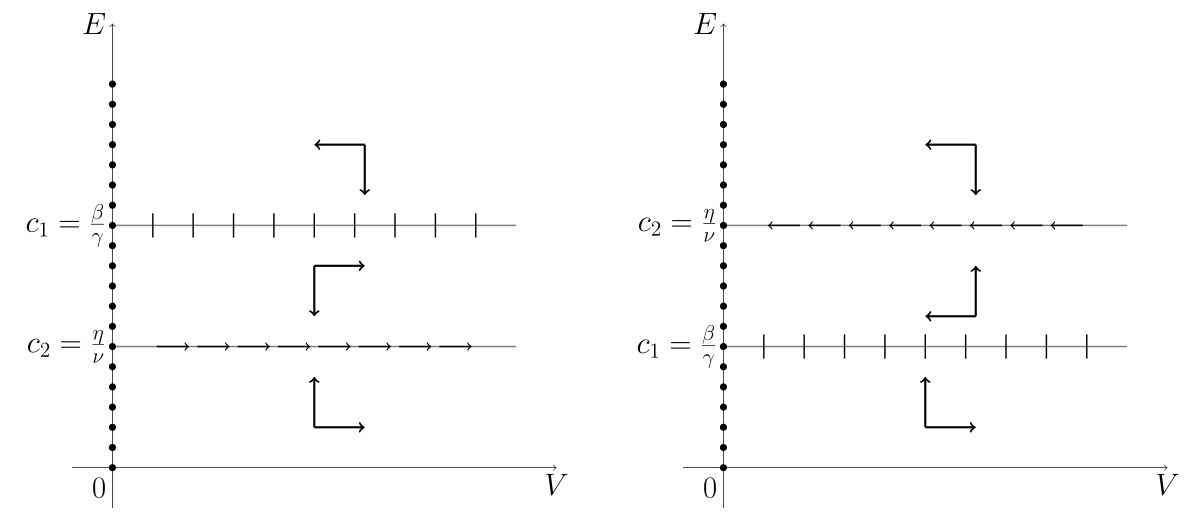
. Mamy więc do czynienia z przypadkiem niehiperbolicznym. Cała oś ![]() składa się z punktów krytycznych układu (12.3), por. rys. 12.3.
składa się z punktów krytycznych układu (12.3), por. rys. 12.3.
Oznaczmy ![]() ,
, ![]() .
Widzimy, że możemy wyznaczyć równanie orbit układu (12.3). Mamy
.
Widzimy, że możemy wyznaczyć równanie orbit układu (12.3). Mamy
| (12.4) |
Zauważmy, że ![]() stanowi rozwiązanie drugiego równania układu, gdyż wtedy
stanowi rozwiązanie drugiego równania układu, gdyż wtedy ![]() . Stąd
. Stąd ![]() i funkcja
i funkcja ![]() zmienia się w sposób wykładniczy. Dla tego rozwiązania w generycznych przypadkach
mamy, jeśli
zmienia się w sposób wykładniczy. Dla tego rozwiązania w generycznych przypadkach
mamy, jeśli ![]() , to
, to ![]() przy
przy ![]() oraz jeśli
oraz jeśli ![]() , to
, to ![]() . Niegeneryczny przypadek
. Niegeneryczny przypadek ![]() pozostawiamy jako ćwiczenie.
pozostawiamy jako ćwiczenie.
Jeśli ![]() , to możemy rozwiązać równanie (12.4). Dostajemy
, to możemy rozwiązać równanie (12.4). Dostajemy
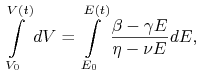 |
skąd
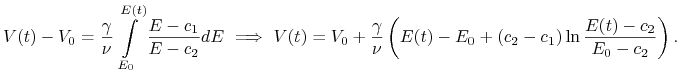 |
(12.5) |
Rozpatrzmy przypadek ![]() , który opisuje silny antygen lub słaby układ odpornościowy, gdyż wtedy
, który opisuje silny antygen lub słaby układ odpornościowy, gdyż wtedy ![]() , co oznacza duży współczynnik namnażania antygenu
, co oznacza duży współczynnik namnażania antygenu ![]() w stosunku do jego śmiertelności w wyniku odpowiedzi odpornościowej (współczynnik
w stosunku do jego śmiertelności w wyniku odpowiedzi odpornościowej (współczynnik ![]() ) i aktywacji układu odpornościowego (
) i aktywacji układu odpornościowego (![]() ), przy dużej śmiertelności efektorów (
), przy dużej śmiertelności efektorów (![]() ). Izoklina
). Izoklina ![]() stanowi separatrysę. Poniżej tej izokliny obie zmienne są rosnące i
stanowi separatrysę. Poniżej tej izokliny obie zmienne są rosnące i ![]() jest ograniczona. Wynika stąd, że
jest ograniczona. Wynika stąd, że ![]() ma granicę, natomiast
ma granicę, natomiast ![]() nie może mieć granicy, gdyż w obszarze
nie może mieć granicy, gdyż w obszarze ![]() nie ma punktów krytycznych o dodatniej współrzędnej
nie ma punktów krytycznych o dodatniej współrzędnej ![]() . Zatem
. Zatem ![]() , co implikuje, że
, co implikuje, że ![]() . W obszarze
. W obszarze ![]() obie zmienne są również monotoniczne, przy czym
obie zmienne są również monotoniczne, przy czym ![]() rośnie, a
rośnie, a ![]() maleje. Skoro obie zmienne pozostają w tym obszarze, to analogicznie jak w pierwszym przypadku otrzymujemy
maleje. Skoro obie zmienne pozostają w tym obszarze, to analogicznie jak w pierwszym przypadku otrzymujemy ![]() . Jeśli orbita zaczyna się w obszarze
. Jeśli orbita zaczyna się w obszarze ![]() , to obie zmienne maleją. Wobec tego orbita albo przechodzi do poprzedniego obszaru, albo ma granicę, zatem dąży do któregoś z punktów krytycznych na osi
, to obie zmienne maleją. Wobec tego orbita albo przechodzi do poprzedniego obszaru, albo ma granicę, zatem dąży do któregoś z punktów krytycznych na osi ![]() . Wtedy na mocy zależności (12.5) granica
. Wtedy na mocy zależności (12.5) granica ![]() spełnia równanie
spełnia równanie
| (12.6) |
Taka dynamika jest w tym przypadku możliwa pod warunkiem, że ![]() , czyli
, czyli
| (12.7) |
Wniosek 12.1
Jeśli ![]() i
i ![]() spełnia nierówność (12.7), to rozwiązania układu (12.3) dążą do punktu krytycznego
spełnia nierówność (12.7), to rozwiązania układu (12.3) dążą do punktu krytycznego ![]() opisanego zależnością (12.6). W przeciwnym przypadku
opisanego zależnością (12.6). W przeciwnym przypadku ![]() i
i ![]() przy
przy ![]() .
.
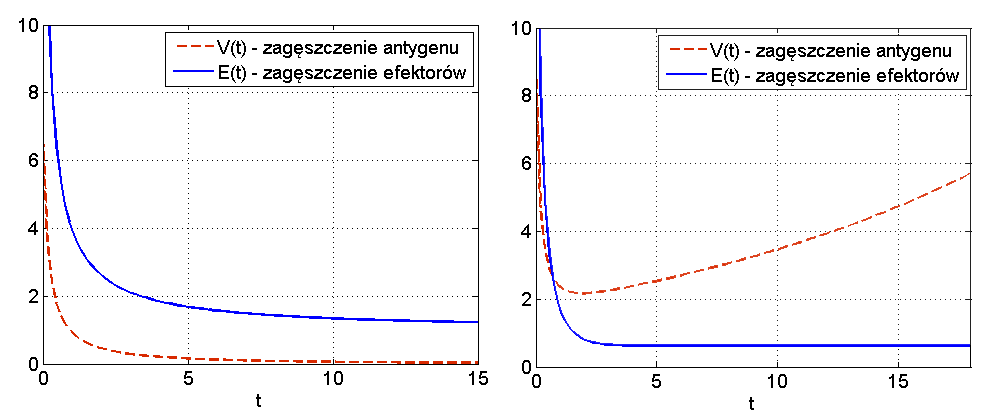
Wniosek 12.1 pokazuje, że jeśli antygen jest silny (spełnia nierówność ![]() ), to wyzdrowienie jest możliwe tylko w przypadku dostatecznie dużego początkowego poziomu efektorów
), to wyzdrowienie jest możliwe tylko w przypadku dostatecznie dużego początkowego poziomu efektorów ![]() oraz stosunkowo niewielkiej początkowej dawki antygenu
oraz stosunkowo niewielkiej początkowej dawki antygenu ![]() spełniającej nierówność (12.7), por. rys. 12.4.
spełniającej nierówność (12.7), por. rys. 12.4.
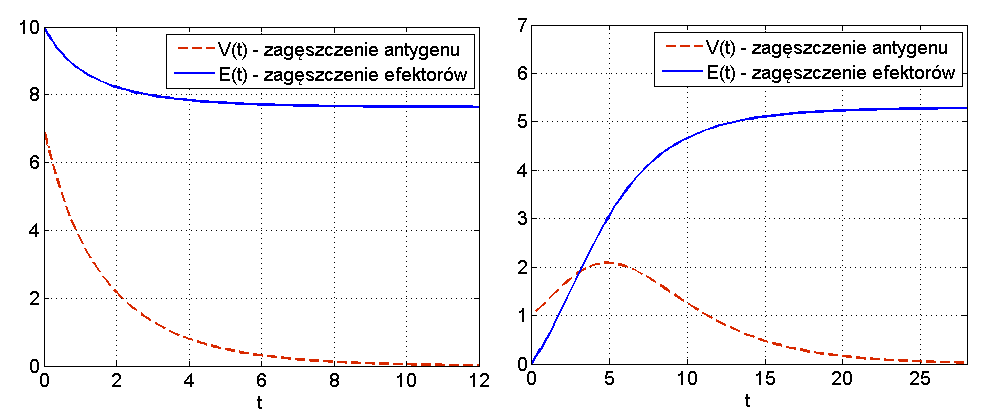
W przypadku słabego antygenu lub dostatecznie silnego układu odpornościowego, czyli dla ![]() , analogiczna analiza pokazuje, że wszystkie rozwiązania zbiegają do któregoś z punktów krytycznych
, analogiczna analiza pokazuje, że wszystkie rozwiązania zbiegają do któregoś z punktów krytycznych ![]() i oczywiście granica
i oczywiście granica ![]() spełnia zależność (12.6). W tej sytuacji mamy zawsze do czynienia z wyzdrowieniem, bez względu na początkową dawkę antygenu. Jeśli poziom efektorów jest dostatecznie duży, to zagęszczenie antygenu stale maleje w czasie, a jeśli jest niezbyt duży w stosunku do początkowej dawki antygenu, to w pierwszej fazie odpowiedzi odpornościowej układ nie może sobie poradzić i zagęszczenie antygenu wzrasta, ale po pewnym czasie wyprodukowana zostanie dostateczna liczba efektorów i poziom antygenu zaczyna maleć, w efekcie maleje do
spełnia zależność (12.6). W tej sytuacji mamy zawsze do czynienia z wyzdrowieniem, bez względu na początkową dawkę antygenu. Jeśli poziom efektorów jest dostatecznie duży, to zagęszczenie antygenu stale maleje w czasie, a jeśli jest niezbyt duży w stosunku do początkowej dawki antygenu, to w pierwszej fazie odpowiedzi odpornościowej układ nie może sobie poradzić i zagęszczenie antygenu wzrasta, ale po pewnym czasie wyprodukowana zostanie dostateczna liczba efektorów i poziom antygenu zaczyna maleć, w efekcie maleje do ![]() , por. rys. 12.5.
, por. rys. 12.5.
Widzimy więc, że układ (12.3) jest zbyt prosty, aby mógł w odpowiedni sposób odzwierciedlić rzeczywiste procesy. W szczególności w rzeczywistości nie jest możliwe, by nawet bardzo silny układ odpornościowy zawsze poradził sobie z antygenem, bez względu na wielkość dawki początkowej.