Zagadnienia

15.1 Podstawy teorii gier
- 15.1.1 Gra w postaci normalnej
15.2 Przykłady gier
- 15.2.1 Gra jastrząb – gołąb
- 15.2.2 Dylemat więźnia

15. Podstawy teorii gier

Na koniec omówimy jeszcze podstawowe pojęcia związane z teorią gier i w ich języku spróbujemy wyjaśnić pewne zachowania osobników, które na pozór wydają się paradoksalne, ale mają głębokie uzasadnienie z punktu widzenia przetrwania gatunku. Zauważmy, że różne gatunki wykształciły różne typy zachowań. Zdarza się, że osobniki danego gatunku prawie nigdy w trakcie rywalizacji — czy o partnera, czy o pożywienie — nie walczą ,,na poważnie”, a tylko straszą się wzajemnie w trakcie tzw. walk rytualnych. W przypadku innych — dochodzi do bardzo poważnych potyczek. Analogiczne zachowania mogą być dyskutowane na gruncie socjologicznym w stosunku np. do pracowników danego przedsiębiorstwa czy innych społeczności. Pojawia się zatem pytanie, kiedy osobnikom bardziej opłaca się stosować strategię walki, a kiedy uniku i od czego taki wybór zależy. Odpowiedzi możemy poszukiwać na gruncie teorii gier w oparciu o strategie ewolucyjnie stabilne.

15.1. Podstawy teorii gier

Teoria gier w nierozerwalny sposób łączy się z dwoma nazwiskami — Johna Maynarda Smitha [15] i Johna Nasha. Pierwszy z nich wprowadził pojęcie strategii ewolucyjnie stabilnej, natomiast drugi sprecyzował matematyczne podstawy tej teorii i zaproponował pojęcie równowagi Nasha.

W teorii gier zakładamy, że co najmniej dwóch osobników ,,gra” w pewną grę. Mają do wyboru pewne zachowania, które nazywamy strategiami. W zależności od tego jakie strategie wybiorą poszczególni gracze, dostają odpowiednie wypłaty. Zatem budując model w oparciu o teorię gier musimy zaproponować zbiór graczy, zbiór strategii oraz macierz wypłat związanych z poszczególnymi strategiami.

15.1.1. Gra w postaci normalnej

Załóżmy, że każdy z graczy ma do wyboru jedną z $M$ strategii $R_{1},\ldots R_{M}$ , które nazwiemy strategiami czystymi. Jeśli założymy, że gracz może wybierać te strategie z pewnymi prawdopodobieństwami $p_{1},\ldots,p_{M}$ , to taki profil strategii $(p_{1},\ldots,p_{M})$ , $p_{i}\geq 0$ , $\sum\limits _{{i=1}}^{M}p_{i}=1$ , nazywamy strategią mieszaną. Strategie mieszane identyfikujemy z punktami sympleksu

$S_{M}=\{ p\in\mathbb{R}^{M}:\ p_{i}\in[0,1],\ \sum\limits _{{i=1}}^{M}p_{i}=1\}.$

Wierzchołki sympleksu $S_{M}$ są oczywiście strategiami czystymi.

Niech w grze bierze udział dwóch graczy i niech $u_{{ij}}$ oznacza wypłatę gracza I jeśli gra on strategią $R_{i}$ przeciwko graczowi II grającemu strategią $R_{j}$ . Macierz $U=(u_{{ij}})_{{i,j=1}}^{M}$ nazywamy macierzą wypłat.

Definicja 15.1

Gra w postaci normalnej dla dwóch graczy zadana jest za pomocą zbioru strategii czystych $R_{1},\ldots,R_{M}$ , sympleksu strategii mieszanych $S_{M}$ oraz macierzy wypłat $U$ .

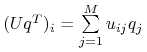Załóżmy teraz, że gracz I gra strategią mieszaną $p=(p_{1},\ldots,p_{M})$ przeciwko graczowi II grającemu strategią mieszaną $q=(q_{1},\ldots,q_{M})$ . Ile wyniesie średnia wypłata gracza I? Gdyby gracz I grał czystą strategią $R_{i}$ przeciwko $q$ , to z prawdopodobieństwami $q_{j}$ dostawałby wypłatę $u_{{ij}}$ , $j=1,\ldots,M$ , czyli średnio $(Uq^{T})_{i}=\sum\limits _{{j=1}}^{M}u_{{ij}}q_{j}$ . 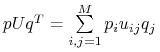Wobec tego grając $p$ przeciw $q$ dostaje z prawdopodobieństwami $p_{i}$ wypłatę $(Uq^{T})_{i}$ , zatem średnio $pUq^{T}=\sum\limits _{{i,j=1}}^{M}p_{i}u_{{ij}}q_{j}$ .

Definicja 15.2

Funkcją odpowiedzi na strategię $q$ nazwiemy funkcję średnich wypłat $F_{q}(p)=pUq^{T}$ .

Niech $\beta(q)$ oznacza zbiór najlepszych odpowiedzi na strategię $q$ , czyli zbiór tych $p$ , dla których $F_{q}(p)$ osiąga wartość maksymalną.

Definicja 15.3

Równowagą Nasha nazwiemy taką strategię $q$ , która jest najlepszą odpowiedzią na siebie samą, czyli $q\in\beta(q)$ . Ścisła równowaga Nasha jest jedyną taką strategią, czyli $\{ q\}=\beta(q)$ .

Widzimy więc, że dla równowagi Nasha zachodzi $pUq^{T}\leq qUq^{T}$ dla dowolnej strategii $p$ , natomiast dla ścisłej równowagi Nasha mamy $pUq^{T}<qUq^{T}$ dla dowolnej strategii $p\ne q$ .

Możemy dość łatwo wykazać, że ścisła równowaga Nasha jest strategią czystą.

Twierdzenie 15.1

Niech $q$ będzie równowagą Nasha. Jeśli $q$ jest ścisłą równowagą Nasha, to istnieje $i$ , dla którego $q=R_{i}$ .

Załóżmy, że dla wszystkich $j\in\{ 1,\ldots,M\}$ mamy $q\ne R_{j}$ . Oczywiście dla dowolnej strategii $p$ zachodzi nierówność $F_{q}(p)<F_{q}(q)$ , a w szczególności

$F_{q}(R_{j})<F_{q}(q),\quad j=1,\ldots,M.$

(15.1)

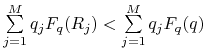Pomnóżmy stronami nierówność (15.1) przez $q_{j}$ i zsumujmy po wszystkich $j=1,\ldots,M$ . Dostaniemy $\sum\limits _{{j=1}}^{M}q_{j}F_{q}(R_{j})<\sum\limits _{{j=1}}^{M}q_{j}F_{q}(q)$ . Zauważmy, że 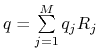$q=\sum\limits _{{j=1}}^{M}q_{j}R_{j}$ , zatem z liniowości $F_{q}$ otrzymujemy $F_{q}(q)<F_{q}(q)$ , czyli $q$ nie może być strategią czystą.

∎

Zauważmy, że gdy $q$ jest ścisłą równowagą Nasha, to jeśli w populacji wszyscy stosują tę strategię, to osobnik, który będzie próbował zastosować inną — przegra, gdyż jego wypłata zawsze będzie mniejsza. Taka dynamika gry wiąże się też z koncepcją strategii ewolucyjnie stabilnej, czyli strategii odpornej na niewielkie zaburzenia.

Definicja 15.4

Strategię $q$ nazwiemy ewolucyjnie stabilną (ESS, czyli evolutionary stable strategie), jeśli dla wszystkich $p\in S_{M}$ , $p\ne q$ zachodzi nierówność

$pU(\varepsilon p+(1-\varepsilon)q)^{T}<qU(\varepsilon p+(1-\varepsilon)q)^{T}$

dla wszystkich dostatecznie małych $\varepsilon<\tilde{\varepsilon}(p)$ .

Stałą $\tilde{\varepsilon}$ nazywamy barierą inwazji. Oczywiście ścisła równowaga Nasha jest strategią ewolucyjnie stabilną. Z drugiej strony

Twierdzenie 15.2

Strategia $q\in S_{M}$ jest ESS wtw spełnione są następujące warunki

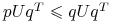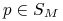równowagi: $pUq^{T}\leq qUq^{T}$ dla wszystkich $p\in S_{M}$ ;
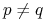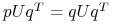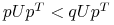stabilności: jeśli dla pewnego $p\ne q$ zachodzi $pUq^{T}=qUq^{T}$ , to $pUp^{T}<qUp^{T}$ .

Dowód tego twierdzenia pozostawiamy jako ćwiczenie.

15.2. Przykłady gier

Omówimy teraz dwa podstawowe przykłady gier i zinterpretujemy ich wyniki.

15.2.1. Gra jastrząb – gołąb

Gra jastrząb – gołąb polega na tym, że gracz ma do wyboru strategię agresji, którą stosując zawsze walczy z przeciwnikiem, albo strategię wycofywania się, w której zawsze ustępuje przeciwnikowi. W trakcie walki osobnik może być poważnie zraniony, więc może wiele stracić, ale z drugiej strony może dużo zyskać, jeśli wygra. Z kolei osobnik ustępujący nie traci w trakcie spotkania z przeciwnikiem. Miarą wygranej w tej grze jest dostosowanie (ang. fitness), często wyrażane jako liczba potomstwa. Niech osobnik, który wygrywa, dostaje $g$ , natomiast osobnik zraniony traci $c$ . Wtedy jeśli spotyka się jastrząb z jastrzębiem, to z prawdopodobieństwem $1/2$ może zyskać $g$ i stracić $c$ , więc średnia wygrana to $(g-c)/2$ . Wygrana jastrzębia przeciw gołębiowi to oczywiście $g$ . Gołąb w starciu z jastrzębiem wycofuje się, więc jego wygrana to $0$ , a w starciu z gołębiem może wygrać z prawdopodobieństwem $1/2$ , więc wygrana to $g/2$ . Gra jest symetryczna, zatem wystarczy podać jedynie macierz wypłat gracza I przeciwko II. Często mówi się o graczu ,,kolumnowym” i ,,wierszowym”. Jeśli przez $R_{1}$ oznaczymy strategię jastrzębia, a przez $R_{2}$ — gołębia, to macierz wypłat ma postać

$\left(\begin{array}[]{cc}\frac{g-c}{2}&g\\ 0&g/2\end{array}\right).$

W grze tej dodatkowo zakładamy, że rany otrzymywane w walce są na tyle dotkliwe, że $g-c<0$ .

Sprawdzimy, że gra ta nie ma ścisłej równowagi Nasha. Wiemy, że taka równowaga musiałaby odpowiadać albo czystej strategii jastrzębia, albo czystej strategii gołębia. Policzmy dla obu strategii funkcje najlepszej odpowiedzi.

Biorąc 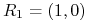$R_{1}=(1,0)$ dostajemy

$F_{{R_{1}}}(p)=pUR_{1}^{T}=(p_{1},1-p_{1})\left(\begin{array}[]{cc}\frac{g-c}{2}&g\\ 0&\frac{g}{2}\end{array}\right)(1,0)^{T}=p_{1}\frac{g-c}{2}$

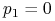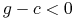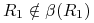i maksymalizując to wyrażenie dostajemy $p_{1}=0$ (tu widzimy, do czego potrzebne jest założenie $g-c<0$ ), czyli $R_{1}\notin\beta(R_{1})$ .
Biorąc 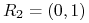$R_{2}=(0,1)$ dostajemy

$F_{{R_{1}}}(p)=pUR_{2}^{T}=(p_{1},1-p_{1})\left(\begin{array}[]{cc}\frac{g-c}{2}&g\\ 0&\frac{g}{2}\end{array}\right)(0,1)^{T}=\frac{(p_{1}+1)g}{2}$

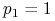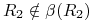i maksymalizując to wyrażenie dostajemy $p_{1}=1$ , czyli $R_{2}\notin\beta(R_{2})$ .

Widzimy więc, że w grze tej nie ma ścisłej równowagi Nasha. Staje się to oczywiste, jeśli wyobrazimy sobie populację składającą się albo z samych jastrzębi, albo z samych gołębi. Jeśli są same jastrzębie, to pojawiający się gołąb ma lepiej, gdyż w starciu z jastrzębiem nic nie traci, zatem gołębie zaczynają się rozprzestrzeniać. Z kolei jeśli są same gołębie, to pojawiający się jastrząb zawsze wygrywa, więc zaczną rozprzestrzeniać się jastrzębie. Wydaje się więc, że powinna być jakaś odpowiednia proporcja między gołębiami i jastrzębiami.

Rozpatrzmy strategię mieszaną $(x,1-x)$ , w której z prawdopodobieństwem $x$ osobnik gra strategię jastrzębia i z prawdopodobieństwem $1-x$ gra gołębia. Wtedy średni wzrost dostosowania jastrzębia wyniesie

$x\frac{g-c}{2}+(1-x)g=g-x\frac{g+c}{2},$

natomiast gołębia

$(1-x)\frac{g}{2}.$

Dopóki któreś z tych dostosowań jest większe, odpowiadająca mu strategia będzie się rozprzestrzeniać. Równowaga ustali się, jeśli oba będą jednakowe, czyli

$g-x\frac{g+c}{2}=(1-x)\frac{g}{2}\Longleftrightarrow x=\frac{g}{c}.$

Zatem proporcja jastrzębi będzie tym mniejsza, im więcej można stracić w walce w stosunku do zysku. Ta analiza wyjaśnia też popularność walk rytualnych wśród zwierząt, które mogą się poważnie zranić w trakcie prawdziwej walki — zamiast faktycznie walczyć zwierzęta te wolą w walce rytualnej zaprezentować przed przeciwnikiem swoją siłę licząc na to, że przeciwnik się zniechęci i odejdzie bez prawdziwej walki. W taki sposób postępują np. jelenie na rykowisku.

15.2.2. Dylemat więźnia

Dylemat więźnia jest typową grą socjologiczną. Zakłada się w niej, że dwóch więźniów zostało osadzonych w więzieniu w osobnych celach i każdemu z nich prokurator obiecał zmniejszenie wyroku za wydanie współwinnego. Jeśli jednak żaden z nich się nie przyzna, to niewiele będzie im można udowodnić, więc obaj dostaną najwyżej niewielki wyrok. Z kolei jeśli jeden z nich zdradzi, a drugi nie, to ten, który wydał współwinnego dostanie wyrok w zawieszeniu. Jeśli obaj zdradzą się wzajemnie, obaj dostaną nieco mniejsze wyroki. Niech macierz wypłat w tej grze przy założeniu, że $R_{1}$ oznacza zdradę kolegi, a $R_{2}$ — odrzucenie propozycji prokuratora, ma postać

$\left(\begin{array}[]{cc}a&0\\ b&c,\end{array}\right)$

gdzie $a$ to wyrok dla więźnia I przy założeniu, że obaj zdradzają się wzajemnie, $b$ — wyrok dla tego więźnia, gdy on odrzuca propozycję prokuratora, a wiezień II go zdradza, więc $b>a$ , natomiast $c$ to wyrok w sytuacji, gdy obaj odrzucają współpracę z prokuratorem, więc $a>c$ .

Zauważmy, że obu więźniom najbardziej opłaca się odrzucić współpracę z prokuratorem, gdyż dzięki temu zapewniają sobie mniejszy wyrok, ale z obawy przed zdradą kolegi wolą sami też zdradzić, bo jeśli kolega zdradzi, a dany więzień nie, to on dostanie cięższy wyrok, niż jeśliby też zdradził. Zatem $R_{1}$ jest tu czystą równowagą Nasha. Faktycznie grając $R_{1}$ przeciw $R_{1}$ mamy wypłatę

$(1,0)\left(\begin{array}[]{cc}a&0\\ b&c,\end{array}\right)(1,0)^{T}=a,$

natomiast grając przeciw dowolnej strategii $(x,1-x)$

$(1,0)\left(\begin{array}[]{cc}a&0\\ b&c,\end{array}\right)(x,1-x)^{T}=ax$

i oczywiście $a>ax$ dla $x\ne 1$ . Wobec tego $R_{1}$ jest ścisłą równowagą Nasha i jednocześnie strategią ewolucyjnie stabilną. Zauważmy jednak, że strategii tej brakuje jednej z podstawowych cech — nie jest optymalna, w tym sensie, że jeśli obaj wybiorą $R_{2}$ , dostaną mniejsze wyroki.

Tego typu zagadnienia możemy rozważać badając np. optymalność w sensie Pareto.

Definicja 15.5

Powiemy, że wynik gry jest nieoptymalny w sensie Pareto, jeżeli istnieje inny wynik, dający albo obu graczom wyższe wypłaty, albo jednemu z nich taką samą, a drugiemu wyższą. W przeciwnym przypadku wynik jest optymalny.

Pareto postulował następujące kryterium: tylko wynik optymalny w sensie Pareto może być akceptowany jako rozwiązanie gry. Kryterium Pareto stanowi podstawową zasadą racjonalności zbiorowej. W dylemacie więźnia wchodzi ona w konflikt z zasadą racjonalności indywidualnej reprezentowanej przez równowagę Nasha.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Modelowanie matematyczne w biologii i medycynie