6. Modele oddziaływań między dwiema populacjami I
Przejdziemy teraz do omówienia zagadnień związanych z modelowaniem ekosystemu, w którym występują dwie populacje. W zależności od oddziaływań między tymi populacjami, rozróżniamy trzy typy ekosystemów
-
układ drapieżnik – ofiara, w którym jeden z gatunków ekosystemu jest pożywieniem dla drugiego;
-
konkurencja, w którym gatunki rywalizują o zasoby środowiska (pożywienie, miejsca lęgowe itp.);
-
symbioza — zjawisko współżycia przynajmniej dwóch gatunków, które wpływają pozytywnie na siebie (mutualizm) lub wyraźne korzyści odnosi jedynie jedna ze stron, nie szkodząc drugiej (komensalizm).
W tym rozdziale zajmiemy się opisem średnich zagęszczeń obu populacji, nie uwzględnimy przestrzennego rozmieszczenia osobników w ekosystemie, co oczywiście kryje dodatkowe założenie, że osobniki są rozmieszczone jednorodnie i jest ich dostatecznie dużo, aby można było mówić o średnim zagęszczeniu.
6.1. Model Lotki – Volterry
Wprowadzimy najpierw pierwszy historycznie model opisujący oddziaływania dwóch populacji w ekosystemie. Dotyczy on układu drapieżnik – ofiara i został zaproponowany równolegle jako model populacyjny przez Vito Volterrę [17] oraz jako model łańcucha reakcji biochemicznych przez Alfreda Lotkę [10]. Volterra zaproponował ten model w celu wyjaśnienia pewnego, zdawałoby się paradoksalnego zjawiska, które zostało zaobserwowane po I wojnie światowej. Po ustaniu działań wojennych, kiedy ludzie na powrót zajęli się uprawianiem swoich zawodów, rybacy odkryli, że populacja ryb drapieżnych w Adriatyku zwiększyła się. Uznano to za paradoks, gdyż zdawałoby się, że wszystkie gatunki powinny ucierpieć w wyniku działań wojennych. Volterra na bazie swojego modelu wykazał, że wzrost liczebności drapieżników był całkiem naturalny, ponieważ w czasie wojny zaprzestano połowów i dzięki temu populacja drapieżników mogła wrócić do stanu naturalnego. Co więcej, model ten odzwierciedla znane w ekologii prawo zachowania średnich, które mówi, że w naturalnych siedliskach zmiany liczebności populacji w czasie zachodzą tak, że zachowana zostaje liczebność średnia.
Zaczniemy od przedstawienia modelu heurystycznego, na bazie którego wyprowadzamy równania modelu Lotki – Volterry. Zakładamy, że w ekosystemie występują dwa gatunki ![]() i
i ![]() , przy czym osobniki drugiego gatunku stanowią pożywienie osobników pierwszego gatunku, czyli drapieżników. Jeśli nie ma drapieżników, to gatunek
, przy czym osobniki drugiego gatunku stanowią pożywienie osobników pierwszego gatunku, czyli drapieżników. Jeśli nie ma drapieżników, to gatunek ![]() ma bardzo dobre warunki i może się rozwijać, podlegając prawu Malthusa ze współczynnikiem rozrodczości
ma bardzo dobre warunki i może się rozwijać, podlegając prawu Malthusa ze współczynnikiem rozrodczości ![]() . Natomiast drapieżniki, jeśli nie ma ofiar, to nie mają co jeść, więc giną z głodu. Jeśli w środowisku są osobniki obu gatunków, to drapieżniki polują na ofiary. Zakładamy, że polowanie jest możliwe tylko w przypadku bezpośredniego kontaktu, osobniki poruszają się losowo, zatem liczba kontaktów jest proporcjonalna do liczebności obu gatunków. Zauważmy, że w takiej sytuacji dla pojedynczego drapieżnika mamy odpowiedź funkcjonalną Hollinga typu I. W związku z polowaniem ubywa osobników gatunku
. Natomiast drapieżniki, jeśli nie ma ofiar, to nie mają co jeść, więc giną z głodu. Jeśli w środowisku są osobniki obu gatunków, to drapieżniki polują na ofiary. Zakładamy, że polowanie jest możliwe tylko w przypadku bezpośredniego kontaktu, osobniki poruszają się losowo, zatem liczba kontaktów jest proporcjonalna do liczebności obu gatunków. Zauważmy, że w takiej sytuacji dla pojedynczego drapieżnika mamy odpowiedź funkcjonalną Hollinga typu I. W związku z polowaniem ubywa osobników gatunku ![]() , proporcjonalnie do liczby spotkań, a współczynnik proporcjonalności odzwierciedla skuteczność drapieżnika. Po upolowaniu ofiary drapieżnik zyskuje energię, której część przeznacza na rozmnażanie.
, proporcjonalnie do liczby spotkań, a współczynnik proporcjonalności odzwierciedla skuteczność drapieżnika. Po upolowaniu ofiary drapieżnik zyskuje energię, której część przeznacza na rozmnażanie.
Niech ![]() oznacza zagęszczenie drapieżników, a
oznacza zagęszczenie drapieżników, a ![]() — zagęszczenie ofiar. Na podstawie powyższego modelu heurystycznego zapiszemy układ równań różniczkowych dynamiki obu populacji
— zagęszczenie ofiar. Na podstawie powyższego modelu heurystycznego zapiszemy układ równań różniczkowych dynamiki obu populacji
![\begin{array}[]{ccl}\dot{V}&=&rV-aVP,\\
\dot{P}&=&-sP+abVP,\end{array}](wyklady/mbm/mi/mi431.png) |
(6.1) |
gdzie dla uproszczenia zapisu pomijamy zmienną niezależną ![]() . Poszczególne składniki układu (6.1) mają następującą interpretację
. Poszczególne składniki układu (6.1) mają następującą interpretację
-
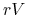 i
i 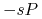 opisują wewnętrzną dynamikę odpowiednio gatunku
opisują wewnętrzną dynamikę odpowiednio gatunku 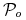 i
i 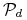 ,
, 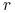 jest współczynnikiem rozrodczości ofiar, a
jest współczynnikiem rozrodczości ofiar, a 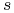 — współczynnikiem śmiertelności drapieżników;
— współczynnikiem śmiertelności drapieżników; -
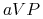 odzwierciedla liczbę losowych spotkań osobników obu gatunków,
odzwierciedla liczbę losowych spotkań osobników obu gatunków, 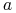 jest współczynnikiem skuteczności polowania, składnik ten interpretujemy także jako biomasę upolowanych ofiar;
jest współczynnikiem skuteczności polowania, składnik ten interpretujemy także jako biomasę upolowanych ofiar; -
współczynnik
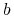 odzwierciedla część upolowanej biomasy, którą gatunek
odzwierciedla część upolowanej biomasy, którą gatunek 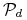 przeznacza na reprodukcję.
przeznacza na reprodukcję.
Przejdziemy teraz do analizy zachowania rozwiązań układu (6.1). Ponieważ układ (6.1) jest autonomiczny, więc bez straty ogólności przyjmujemy, że ![]() i
i ![]() ,
, ![]() .
Sformułujemy najpierw następujące stwierdzenie.
.
Sformułujemy najpierw następujące stwierdzenie.
Stwierdzenie 6.1
Rozwiązania układu (6.1) dla nieujemnego warunku początkowego ![]() ,
, ![]() ,
, ![]() , istnieją dla wszystkich
, istnieją dla wszystkich ![]() , są jednoznaczne i nieujemne.
, są jednoznaczne i nieujemne.
Ponieważ prawa strona układu (6.1) jest klasy ![]() (nawet analityczna) w
(nawet analityczna) w ![]() , to lokalne rozwiązania istnieją dla dowolnego warunku początkowego i są one jednoznaczne. Niech
, to lokalne rozwiązania istnieją dla dowolnego warunku początkowego i są one jednoznaczne. Niech ![]() będzie przedziałem określoności rozwiązania dla warunku początkowego
będzie przedziałem określoności rozwiązania dla warunku początkowego ![]() . Pokażemy, że rozwiązanie to jest nieujemne. Niech
. Pokażemy, że rozwiązanie to jest nieujemne. Niech ![]() . Wtedy
. Wtedy ![]() i zmienna
i zmienna ![]() nie zmienia się. Mamy więc
nie zmienia się. Mamy więc ![]() i wtedy
i wtedy ![]() , czyli
, czyli ![]() . Analogicznie dla
. Analogicznie dla ![]() mamy
mamy ![]() i
i ![]() . Niech teraz
. Niech teraz ![]() ,
, ![]() . Załóżmy, że istnieje taka chwila
. Załóżmy, że istnieje taka chwila ![]() , że zmienna
, że zmienna ![]() staje się ujemna. Wtedy
staje się ujemna. Wtedy ![]() , co jest sprzeczne z jednoznacznością rozwiązań, czyli
, co jest sprzeczne z jednoznacznością rozwiązań, czyli ![]() dla wszystkich
dla wszystkich ![]() , dla których rozwiązanie istnieje. Podobnie
, dla których rozwiązanie istnieje. Podobnie ![]() dla
dla ![]() .
.
Pozostaje jeszcze udowodnić istnienie rozwiązań dla wszystkich ![]() .
Załóżmy, że rozwiązanie istnieje na pewnym skończonym przedziale
.
Załóżmy, że rozwiązanie istnieje na pewnym skończonym przedziale ![]() Wiemy już, że rozwiązanie jest nieujemne, więc
Wiemy już, że rozwiązanie jest nieujemne, więc
Po pomnożeniu powyższej nierówności przez ![]() dostajemy
dostajemy
czyli ![]() dla
dla ![]() , więc
, więc ![]() . Stąd dla dowolnego skończonego
. Stąd dla dowolnego skończonego ![]() zachodzi
zachodzi
![]() oraz
oraz ![]() . Teraz możemy oszacować pochodną zmiennej
. Teraz możemy oszacować pochodną zmiennej ![]() . Dla
. Dla ![]() otrzymujemy
otrzymujemy
![]() , czyli
, czyli ![]() oraz
oraz ![]() .
Szacując pochodne z dołu dostajemy
.
Szacując pochodne z dołu dostajemy ![]() oraz
oraz
![]() . Mamy więc funkcje ograniczone o ograniczonych pochodnych, z czego wynika, że istnieją granice
. Mamy więc funkcje ograniczone o ograniczonych pochodnych, z czego wynika, że istnieją granice ![]() oraz
oraz
![]() .
Gdyby któraś z tych granic nie istniała, to możemy wybrać dwa podciągi zbieżne do różnych granic. Niech np.
.
Gdyby któraś z tych granic nie istniała, to możemy wybrać dwa podciągi zbieżne do różnych granic. Niech np. ![]() oraz
oraz ![]() dla
dla ![]() ,
, ![]() i
i ![]() . Wtedy z twierdzenia o wartości średniej
. Wtedy z twierdzenia o wartości średniej ![]() przy
przy ![]() , co jest sprzeczne z ograniczonością pochodnej.
Biorąc warunek początkowy
, co jest sprzeczne z ograniczonością pochodnej.
Biorąc warunek początkowy ![]() ,
,
![]() ,
, ![]() i korzystając z twierdzenia o istnieniu i jednoznaczności rozwiązań przedłużamy rozwiązanie dla
i korzystając z twierdzenia o istnieniu i jednoznaczności rozwiązań przedłużamy rozwiązanie dla ![]() . Wobec dowolności
. Wobec dowolności
![]() rozwiązanie istnieje dla wszystkich
rozwiązanie istnieje dla wszystkich ![]() .
.
Zauważmy, że gładkość prawej strony i liniowe oszacowanie pochodnej zawsze gwarantuje przedłużalność rozwiązań.
Przystąpimy teraz do analizy asymptotyki rozwiązań układu (6.1). Wyznaczymy najpierw stany stacjonarne ![]() . Spełniają one układ równań
. Spełniają one układ równań
zatem albo ![]() , albo
, albo ![]() .
Lokalną stabilność spróbujemy zbadać stosując metodę linearyzacji.
Macierz Jacobiego układu (6.1) ma postać
.
Lokalną stabilność spróbujemy zbadać stosując metodę linearyzacji.
Macierz Jacobiego układu (6.1) ma postać
Dla zerowego stanu stacjonarnego otrzymujemy
widzimy więc, że jest to punkt siodłowy, gdyż wartości własne
![]() ,
, ![]() mają różne znaki.
Z kolei dla dodatniego stanu stacjonarnego
mają różne znaki.
Z kolei dla dodatniego stanu stacjonarnego
czyli wartości własne macierzy Jacobiego
![]() są czysto urojone, zatem nie jest
spełnione założenie twierdzenia o linearyzacji dotyczące hiperboliczności układu [13] i nie możemy w tym przypadku skorzystać z tej metody.
są czysto urojone, zatem nie jest
spełnione założenie twierdzenia o linearyzacji dotyczące hiperboliczności układu [13] i nie możemy w tym przypadku skorzystać z tej metody.
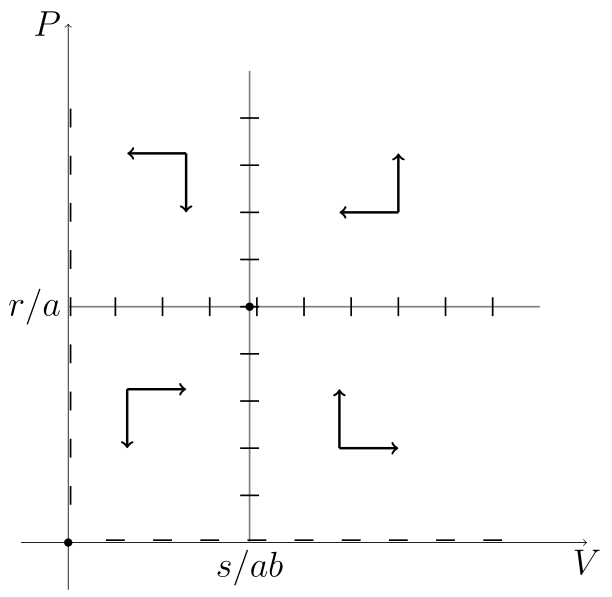
Spróbujmy naszkicować portret fazowy. Zaczniemy od wyznaczenia izoklin zerowych, czyli krzywych, na których ![]() (izoklina zerowa zmiennej
(izoklina zerowa zmiennej ![]() ) albo
) albo ![]() (izoklina zerowa zmiennej
(izoklina zerowa zmiennej ![]() ). Mamy
). Mamy
oraz
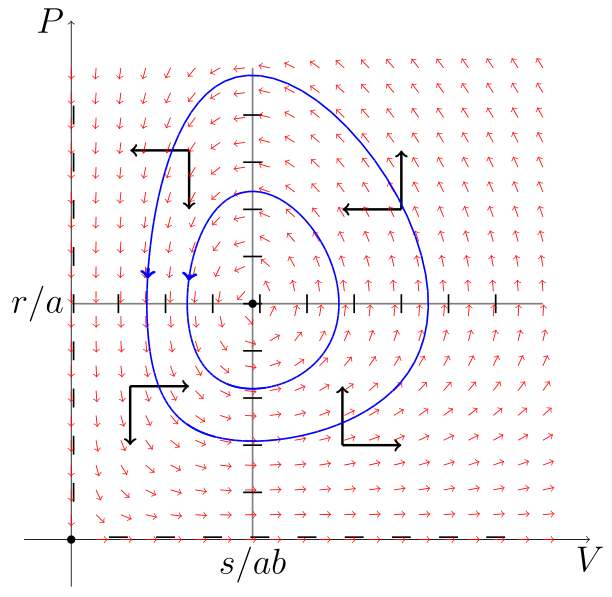
Izokliny zerowe dzielą przestrzeń fazową ![]() na cztery podprzestrzenie, w których poszczególne zmienne mają ustalony kierunek przebiegu, por. rys. 6.1. Widzimy, że otrzymane w taki sposób pole wektorowe pokazuje, że rozwiązania okrążają dodatni stan stacjonarny
na cztery podprzestrzenie, w których poszczególne zmienne mają ustalony kierunek przebiegu, por. rys. 6.1. Widzimy, że otrzymane w taki sposób pole wektorowe pokazuje, że rozwiązania okrążają dodatni stan stacjonarny ![]() .
.
Można pokazać, że wszystkie rozwiązania są okresowe, co wynika z własności całki pierwszej [13] układu (6.1). Znalezienie całki pierwszej i zbadanie jej własności pozostawiamy jako ćwiczenie.
Na koniec zauważmy, że wszystkie rozwiązania oscylują wokół stanu stacjonarnego
![]() , por. rys. 6.2. Pokażemy, że każde rozwiązanie ma wartość średnią równą współrzędnym tego stanu. Niech
, por. rys. 6.2. Pokażemy, że każde rozwiązanie ma wartość średnią równą współrzędnym tego stanu. Niech ![]() oznacza okres rozwiązania
oznacza okres rozwiązania ![]() .
.
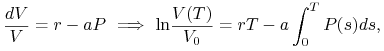 |
a ponieważ rozwiązanie jest okresowe, to ![]() , czyli
, czyli
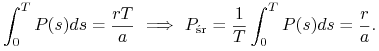 |
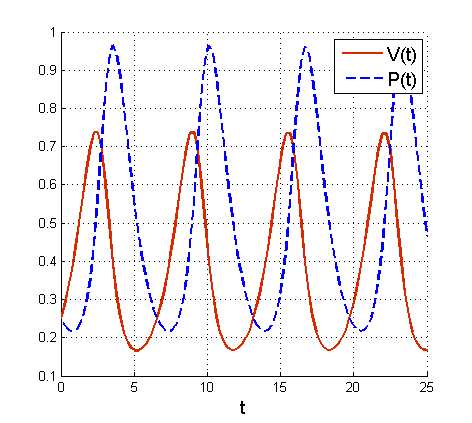
Analogicznie pokazujemy, że ![]() . Rozwiązania oscylują wokół stanu stacjonarnego, przy czym oscylacje populacji drapieżników i ofiar są przesunięte w fazie, por. rys. 6.3.
. Rozwiązania oscylują wokół stanu stacjonarnego, przy czym oscylacje populacji drapieżników i ofiar są przesunięte w fazie, por. rys. 6.3.
Na tej podstawie wyjaśnimy paradoks związany z populacją ryb drapieżnych w Adriatyku. Zauważmy, że jeśli odławiamy ryby, to zakładając jednakową intensywność odłowu dla obu populacji ![]() i
i ![]() , otrzymamy następującą modyfikację układu (6.1)
, otrzymamy następującą modyfikację układu (6.1)
![\begin{array}[]{ccl}\dot{V}&=&(r-\gamma)V-aVP,\\
\dot{P}&=&-(s+\gamma)P+abVP,\end{array}](wyklady/mbm/mi/mi446.png) |
(6.2) |
gdzie ![]() oznacza współczynnik odłowu. Zauważmy dalej, że aby populacja ofiar nie wyginęła, musimy dokonywać odłowów w sposób sensowny, tak by
oznacza współczynnik odłowu. Zauważmy dalej, że aby populacja ofiar nie wyginęła, musimy dokonywać odłowów w sposób sensowny, tak by ![]() . Jeśli łowimy zbyt dużo,
. Jeśli łowimy zbyt dużo, ![]() , to
, to ![]() dla wszystkich
dla wszystkich ![]() i populacja ginie. Natomiast gdy
i populacja ginie. Natomiast gdy ![]() , to układ (6.2) ma dokładnie taką samą postać jak (6.1), więc odławiane populacje mają średnie zagęszczenia równe
, to układ (6.2) ma dokładnie taką samą postać jak (6.1), więc odławiane populacje mają średnie zagęszczenia równe
zatem odławianie powoduje zmniejszenie średniej liczebności populacji drapieżników i zwiększenie średniej liczebności populacji ofiar. W związku z tym w czasie gdy nie było połowów, populacje wróciły do stanu naturalnego, więc liczebność drapieżników wzrosła.
6.2. Konstruktywna krytyka modelu Lotki – Volterry
Chociaż model Lotki – Volterry odzwierciedla obserwowane w naturze oscylacje w układach drapieżnik – ofiara, a także w sposób analityczny dowodzi ekologicznego prawa zachowania średnich w tych układach, to jednak nie jest pozbawiony wad. Przede wszystkim z matematycznego punktu widzenia jego główną wadę stanowi brak stabilności strukturalnej. Pojęcie stabilności strukturalnej wykracza poza ramy tego wykładu — w skrócie stabilność strukturalna oznacza, że niewielka zmiana prawej strony układu nie prowadzi do radykalnych zmian w dynamice rozwiązań. Widzimy, że w przypadku układu (6.1) nawet bardzo mała zmiana prawej strony może skutkować zmianą typu stanu stacjonarnego — stan typu centrum bardzo łatwo zaburzyć. Dodatkowo model ma też pewną własność, która podlega krytyce z ekologicznego punktu widzenia. Rozwiązania układu (6.1) oscylują w taki sposób, że wzrost populacji drapieżników poprzedza wzrost populacji ofiar, natomiast w większości rzeczywistych układów drapieżnik – ofiara takie oscylacje są przesunięte w stosunku do tych rozwiązań; najpierw obserwujemy wzrost populacji ofiar, a potem następujący po nim wzrost populacji drapieżników. Należy też zauważyć, że w modelu heurystycznym pominięto wiele istotnych dla układów drapieżnik – ofiara czynników. W związku z tym model Lotki – Volterry był na wiele różnych sposobów modyfikowany i poniżej omówimy pokrótce kilka z tych modyfikacji.