8. Modele oddziaływań między dwiema populacjami III
8.1. Układ konkurujących gatunków
Korzystając z doświadczeń związanych z omówionymi już modelami oddziaływań typu drapieżnik – ofiara przejdziemy teraz do opisu oddziaływań innego typu. Jak poprzednio zakładamy, że w środowisku występują dwa gatunki ![]() i
i ![]() , ale tym razem osobniki tych gatunków konkurują ze sobą o zasoby środowiska. Zwykle budując taki model przyjmujemy, że jest to konkurencja o pożywienie, ale może ona dotyczyć także dostępnej przestrzeni życiowej, a często
mamy do czynienia z obydwoma rodzajami konkurencji.
Ponieważ gatunki konkurują ze sobą, to nie widać powodu do wyróżniania któregokolwiek z nich, zatem opis powinien być symetryczny — jeśli zamienimy te gatunki i nazwiemy gatunek
, ale tym razem osobniki tych gatunków konkurują ze sobą o zasoby środowiska. Zwykle budując taki model przyjmujemy, że jest to konkurencja o pożywienie, ale może ona dotyczyć także dostępnej przestrzeni życiowej, a często
mamy do czynienia z obydwoma rodzajami konkurencji.
Ponieważ gatunki konkurują ze sobą, to nie widać powodu do wyróżniania któregokolwiek z nich, zatem opis powinien być symetryczny — jeśli zamienimy te gatunki i nazwiemy gatunek ![]() (
(![]() ,
, ![]() ) gatunkiem
) gatunkiem ![]() (
(![]() ,
, ![]() ) i na odwrót, to układ powinien pozostać taki sam.
) i na odwrót, to układ powinien pozostać taki sam.
Skoro mamy skorzystać z nabytych doświadczeń, zbudujemy model w oparciu o wewnętrzną dynamikę logistyczną dla każdego z gatunków ![]() . Wobec tego, jeśli w środowisku występuje tylko jeden z tych gatunków, to jego zagęszczenie
. Wobec tego, jeśli w środowisku występuje tylko jeden z tych gatunków, to jego zagęszczenie ![]() w chwili
w chwili ![]() opisuje równanie
opisuje równanie
gdzie ![]() oznacza współczynnik rozrodczości netto dla gatunku
oznacza współczynnik rozrodczości netto dla gatunku ![]() , zaś
, zaś ![]() — pojemność środowiska dla tego gatunku. Oczywiście założenie ograniczonej pojemności środowiska implikuje też występowanie konkurencji między osobnikami tego samego gatunku. Tę konkurencję nazywamy w tym kontekście konkurencją wewnątrzgatunkową lub krócej — konkurencją wewnętrzną. Oprócz tego mamy też do czynienia z konkurencją zewnątrzgatunkową, albo konkurencją zewnętrzną, którą opisujemy podobnie do konkurencji wewnętrznej. Zakładamy więc, że osobniki konkurują ze sobą w trakcie spotkań między dwoma osobnikami różnego gatunku i liczba tych spotkań jest proporcjonalna do liczebności każdego z gatunków
— pojemność środowiska dla tego gatunku. Oczywiście założenie ograniczonej pojemności środowiska implikuje też występowanie konkurencji między osobnikami tego samego gatunku. Tę konkurencję nazywamy w tym kontekście konkurencją wewnątrzgatunkową lub krócej — konkurencją wewnętrzną. Oprócz tego mamy też do czynienia z konkurencją zewnątrzgatunkową, albo konkurencją zewnętrzną, którą opisujemy podobnie do konkurencji wewnętrznej. Zakładamy więc, że osobniki konkurują ze sobą w trakcie spotkań między dwoma osobnikami różnego gatunku i liczba tych spotkań jest proporcjonalna do liczebności każdego z gatunków ![]() ,
, ![]() ,
, ![]() . Wobec tego składnik konkurencji zewnętrznej w obu równaniach układu jest proporcjonalny do
. Wobec tego składnik konkurencji zewnętrznej w obu równaniach układu jest proporcjonalny do ![]() .
.
Ostatecznie otrzymujemy dwóch układ równań
![\begin{array}[]{ccl}\dot{N}_{1}&=&r_{1}N_{1}\left(1-\frac{N_{1}}{K_{1}}-a_{{12}}\frac{N_{2}}{K_{2}}\right),\\
\dot{N}_{2}&=&r_{2}N_{2}\left(1-\frac{N_{2}}{K_{2}}-a_{{21}}\frac{N_{1}}{K_{1}}\right),\end{array}](wyklady/mbm/mi/mi695.png) |
(8.1) |
gdzie ![]() są współczynnikami konkurencji zewnętrznej, przy czym dla uproszczenia obliczeń związanych z układem (8.1) współczynnik ten odnosi się do liczebności populacji
są współczynnikami konkurencji zewnętrznej, przy czym dla uproszczenia obliczeń związanych z układem (8.1) współczynnik ten odnosi się do liczebności populacji ![]() w stosunku do jej pojemności środowiska.
Zauważmy, że dzięki takiemu zapisowi możemy łatwo przeprowadzić ubezwymiarowienie układu (8.1) wprowadzając zmienne
w stosunku do jej pojemności środowiska.
Zauważmy, że dzięki takiemu zapisowi możemy łatwo przeprowadzić ubezwymiarowienie układu (8.1) wprowadzając zmienne ![]() ,
, ![]() . Przypomnijmy, że taką zamianę zmiennych wprowadziliśmy w przypadku dyskretnego równania logistycznego, co umożliwiło ograniczenie rozważań do odcinka
. Przypomnijmy, że taką zamianę zmiennych wprowadziliśmy w przypadku dyskretnego równania logistycznego, co umożliwiło ograniczenie rozważań do odcinka ![]() . W nowych zmiennych układ (8.1) przyjmuje postać
. W nowych zmiennych układ (8.1) przyjmuje postać
| (8.2) |
przy czym ![]() odzwierciedla procentową eksploatację środowiska przez gatunek
odzwierciedla procentową eksploatację środowiska przez gatunek ![]() .
.
Przeprowadzimy teraz analizę dynamiki modelu konkurujących gatunków opisanego przez układ (8.2) podobnie jak dla układu (6.1). Zaczniemy od zbadania podstawowych własności takich jak istnienie, jednoznaczność, nieujemność rozwiązań dla nieujemnych warunków początkowych.
Stwierdzenie 8.1
Niech ![]() ,
, ![]() ,
, ![]() , będzie warunkiem początkowym dla układu (8.2). Dla danego warunku początkowego istnieje jednoznaczne, nieujemne rozwiązanie określone dla wszystkich
, będzie warunkiem początkowym dla układu (8.2). Dla danego warunku początkowego istnieje jednoznaczne, nieujemne rozwiązanie określone dla wszystkich ![]() . Co więcej, rozwiązanie jest ograniczone,
. Co więcej, rozwiązanie jest ograniczone,
![]() ,
, ![]() ,
, ![]() .
.
Istnienie i jednoznaczność łatwo wykazać korzystając z tego, że prawa strona układu jest funkcją klasy ![]() . Nieujemność rozwiązań wynika np. z postaci logarytmicznej
. Nieujemność rozwiązań wynika np. z postaci logarytmicznej
natomiast przedłużalność wnioskujemy bezpośrednio z nieujemności, gdyż
a jeśli prawa strona układu ma liniowe oszacowanie, to rozwiązania istnieją dla wszystkich ![]() . Co więcej, ograniczoność rozwiązań także wynika z ich nieujemności, gdyż zamiast powyższego liniowego oszacowania możemy wziąć
. Co więcej, ograniczoność rozwiązań także wynika z ich nieujemności, gdyż zamiast powyższego liniowego oszacowania możemy wziąć
i korzystając z nierówności różniczkowych oszacować z góry rozwiązania układu (8.1) przez rozwiązania równania logistycznego z pojemnością środowiska ![]() , analogicznie jak w przypadku układu (7.1).
, analogicznie jak w przypadku układu (7.1).
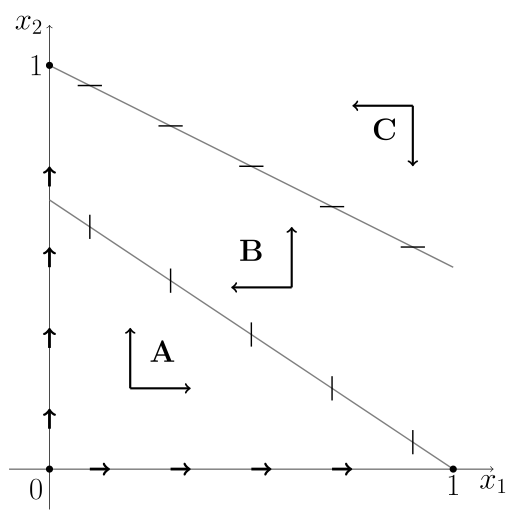
Po zbadaniu podstawowych własności możemy przejść do przeanalizowania portretu fazowego. Izokliny zerowe układu (8.2) wyznaczamy jako
-
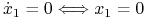 lub
lub 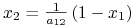 ;
; -
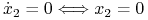 lub
lub 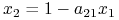 .
.
Wzajemne położenie izoklin nietrywialnych zależy od wielkości współczynników ![]() . Mamy trzy istotnie różne przypadki generyczne
. Mamy trzy istotnie różne przypadki generyczne
-
jeden ze współczynników jest większy, a drugi mniejszy niż 1 — założymy, że
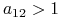 i
i 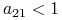 , drugi układ parametrów implikuje taką samą dynamikę z dokładnością do zamiany miejscami gatunków
, drugi układ parametrów implikuje taką samą dynamikę z dokładnością do zamiany miejscami gatunków 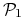 i
i 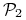 ;
; -
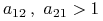 ;
; -
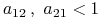 .
.
Oprócz wymienionych powyżej przypadków generycznych mamy też przypadki niegeneryczne, gdy co najmniej jeden ze współczynników konkurencji jest równy ![]() . Analizę tych przypadków pomijamy. Od strony biologicznej nieprawdopodobne wydaje się, żeby wartość jakiegokolwiek parametru utrzymywała się na stałym poziomie — zwykle występują drobne wahania, a co za tym idzie przypadki niegeneryczne są nieistotne z biologicznego punktu widzenia.
. Analizę tych przypadków pomijamy. Od strony biologicznej nieprawdopodobne wydaje się, żeby wartość jakiegokolwiek parametru utrzymywała się na stałym poziomie — zwykle występują drobne wahania, a co za tym idzie przypadki niegeneryczne są nieistotne z biologicznego punktu widzenia.
Zbadajmy najpierw stany stacjonarne i ich stabilność. Mamy zawsze trzy stany stacjonarne na brzegu przestrzeni fazowej ![]() :
: ![]() ,
, ![]() i
i ![]() , które odzwierciedlają wymarcie co najmniej jednego z gatunków. Jeśli nietrywialne izokliny przecinają się, to mamy dodatni stan stacjonarny
, które odzwierciedlają wymarcie co najmniej jednego z gatunków. Jeśli nietrywialne izokliny przecinają się, to mamy dodatni stan stacjonarny
Widzimy, że dodatni stan stacjonarny istnieje, jeśli albo oba współczynniki ![]() są poniżej
są poniżej ![]() , albo oba są powyżej. W celu zbadania stabilności wyznaczamy macierz Jacobiego
, albo oba są powyżej. W celu zbadania stabilności wyznaczamy macierz Jacobiego
i obliczamy wartości własne
-
dla
 mamy
mamy 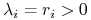 ,
, 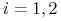 ;
; -
dla
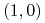 :
: 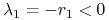 ,
, 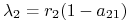 i dla
i dla 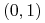 — symetrycznie;
— symetrycznie; -
dla
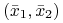 wartości własne są rozwiązaniami równania charakterystycznego
wartości własne są rozwiązaniami równania charakterystycznego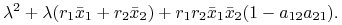
Wynika stąd, że ![]() jest zawsze węzłem niestabilnym, stabilność
jest zawsze węzłem niestabilnym, stabilność ![]() zależy od parametru
zależy od parametru ![]() — jeśli
— jeśli ![]() , to mamy węzeł stabilny, a jeśli
, to mamy węzeł stabilny, a jeśli ![]() , to siodło (analogicznie dla
, to siodło (analogicznie dla ![]() w zależności od
w zależności od ![]() ). Natomiast stabilność dodatniego stanu stacjonarnego zależy od iloczynu
). Natomiast stabilność dodatniego stanu stacjonarnego zależy od iloczynu ![]() — jeśli jest on większy niż 1, to
— jeśli jest on większy niż 1, to ![]() jest siodłem, a dla nierówności przeciwnej — stabilnym węzłem. We wszystkich tych przypadkach następuje bifurkacja siodło – węzeł dla krytycznej wartości parametrów (czyli gdy są równe
jest siodłem, a dla nierówności przeciwnej — stabilnym węzłem. We wszystkich tych przypadkach następuje bifurkacja siodło – węzeł dla krytycznej wartości parametrów (czyli gdy są równe ![]() ).
).
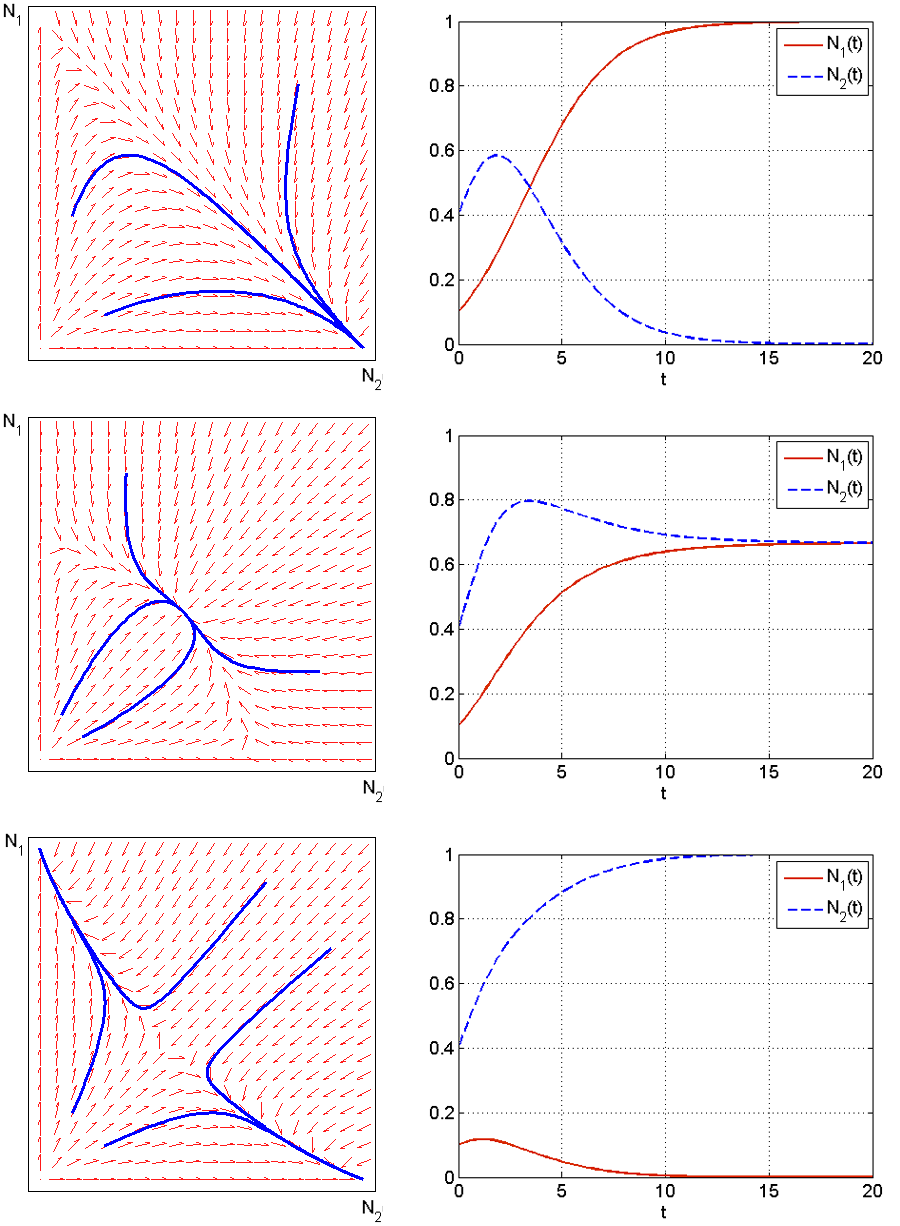
Analizę zachowania rozwiązań w przestrzeni fazowej ![]() zaczniemy od przypadku 1, tj.
zaczniemy od przypadku 1, tj. ![]() . Przy takim układzie parametrów nietrywialne izokliny dla zmiennych
. Przy takim układzie parametrów nietrywialne izokliny dla zmiennych ![]() i
i ![]() nie przecinają się w omawianej przestrzeni fazowej — nie istnieje dodatni stan stacjonarny. Wiemy już, że
nie przecinają się w omawianej przestrzeni fazowej — nie istnieje dodatni stan stacjonarny. Wiemy już, że ![]() jest siodłem, a
jest siodłem, a ![]() węzłem stabilnym. Izokliny dzielą przestrzeń fazową na 3 obszary: obszar
węzłem stabilnym. Izokliny dzielą przestrzeń fazową na 3 obszary: obszar ![]() pod izokliną dla
pod izokliną dla ![]() , obszar
, obszar ![]() pomiędzy izoklinami oraz
pomiędzy izoklinami oraz ![]() — powyżej izokliny dla
— powyżej izokliny dla ![]() , por. rys. 8.1.
, por. rys. 8.1.
Zauważmy, że izokliny trywialne ![]() oraz
oraz ![]() stanowią rozwiązania układu. Rzeczywiście, jeśli
stanowią rozwiązania układu. Rzeczywiście, jeśli ![]() , to
, to ![]() i stąd
i stąd ![]() dla
dla ![]() . Wtedy
. Wtedy ![]() i
i ![]() spełnia równanie logistyczne, zatem na osi pionowej rozwiązanie zbiega do punktu
spełnia równanie logistyczne, zatem na osi pionowej rozwiązanie zbiega do punktu ![]() . Dokładnie takie samo rozumowanie pokazuje, że na osi poziomej rozwiązanie zbiega do
. Dokładnie takie samo rozumowanie pokazuje, że na osi poziomej rozwiązanie zbiega do ![]() . Ponieważ ten ostatni punkt jest siodłem, więc wyznaczyliśmy w ten sposób rozmaitość stabilną. Z przebiegu pola wektorowego w otoczeniu punktu
. Ponieważ ten ostatni punkt jest siodłem, więc wyznaczyliśmy w ten sposób rozmaitość stabilną. Z przebiegu pola wektorowego w otoczeniu punktu ![]() wnioskujemy, że interesujący nas fragment rozmaitości niestabilnej przebiega w obszarze
wnioskujemy, że interesujący nas fragment rozmaitości niestabilnej przebiega w obszarze ![]() . W obszarze
. W obszarze ![]() obie zmienne rosną, nie mogą pozostać w tym obszarze, bo musiałyby być zbieżne do punktu o dodatnich współrzędnych na izoklinie dla zmiennej
obie zmienne rosną, nie mogą pozostać w tym obszarze, bo musiałyby być zbieżne do punktu o dodatnich współrzędnych na izoklinie dla zmiennej ![]() — ale taki punkt musiałby wtedy być stanem stacjonarnym, a nie ma dodatniego stanu stacjonarnego w tym przypadku. Wobec tego rozwiązanie przechodzi do obszaru
— ale taki punkt musiałby wtedy być stanem stacjonarnym, a nie ma dodatniego stanu stacjonarnego w tym przypadku. Wobec tego rozwiązanie przechodzi do obszaru ![]() . Z kolei jeśli punkt początkowy należy do
. Z kolei jeśli punkt początkowy należy do ![]() , to obie zmienne maleją i analogiczne rozumowanie pokazuje, że albo rozwiązanie zostaje w
, to obie zmienne maleją i analogiczne rozumowanie pokazuje, że albo rozwiązanie zostaje w ![]() i wtedy zbiega do stanu stacjonarnego
i wtedy zbiega do stanu stacjonarnego ![]() , albo przechodzi do obszaru
, albo przechodzi do obszaru ![]() . Przebieg pola wektorowego pokazuje, że rozwiązanie nie może wyjść z obszaru
. Przebieg pola wektorowego pokazuje, że rozwiązanie nie może wyjść z obszaru ![]() , a ponieważ w tym obszarze jest także monotoniczne —
, a ponieważ w tym obszarze jest także monotoniczne — ![]() maleje a
maleje a ![]() rośnie — to zbiega do stanu stacjonarnego, czyli do
rośnie — to zbiega do stanu stacjonarnego, czyli do ![]() . Rozmaitość niestabilna stanowi separatrysę, która oddziela rozwiązania zaczynające się w
. Rozmaitość niestabilna stanowi separatrysę, która oddziela rozwiązania zaczynające się w ![]() (dokładniej, jeśli przeprowadzimy analizę przebiegu takich rozwiązań dla
(dokładniej, jeśli przeprowadzimy analizę przebiegu takich rozwiązań dla ![]() , to zauważymy, że zbiegają one do
, to zauważymy, że zbiegają one do ![]() przy
przy ![]() ) i w związku z tym mające taką własność, że
) i w związku z tym mające taką własność, że ![]() stale rośnie (pod izokliną dla zmiennej
stale rośnie (pod izokliną dla zmiennej ![]() ), natomiast
), natomiast ![]() najpierw rośnie, osiąga wartość maksymalną przekraczając izoklinę, a następnie maleje — musi więc maleć do
najpierw rośnie, osiąga wartość maksymalną przekraczając izoklinę, a następnie maleje — musi więc maleć do ![]() , od rozwiązań zaczynających się w
, od rozwiązań zaczynających się w ![]() i przechodzących do
i przechodzących do ![]() — takie rozwiązanie ma malejącą pierwszą współrzędną, natomiast druga współrzędna osiąga minimum na izoklinie, a następnie rośnie do
— takie rozwiązanie ma malejącą pierwszą współrzędną, natomiast druga współrzędna osiąga minimum na izoklinie, a następnie rośnie do ![]() . Ostatecznie wszystkie rozwiązania oprócz
. Ostatecznie wszystkie rozwiązania oprócz ![]() zbiegają asymptotycznie do stanu stacjonarnego
zbiegają asymptotycznie do stanu stacjonarnego ![]() i są od pewnego miejsca monotoniczne. Wnioskujemy, że w tym przypadku gatunek
i są od pewnego miejsca monotoniczne. Wnioskujemy, że w tym przypadku gatunek ![]() ginie, natomiast
ginie, natomiast ![]() stabilizuje się na poziomie pojemności środowiska.
stabilizuje się na poziomie pojemności środowiska.
Wspomnieliśmy już, że jeśli układ parametrów ![]() i
i ![]() zmienia się, tj. gdy
zmienia się, tj. gdy ![]() to rozwiązania zachowują się symetrycznie — dostajemy więc zbieżność wszystkich dodatnich rozwiązań do
to rozwiązania zachowują się symetrycznie — dostajemy więc zbieżność wszystkich dodatnich rozwiązań do ![]() . Opisany przebieg rozwiązań wiąże się z tym, że konkurencja zewnętrzna okazuje się znacznie bardziej niebezpieczna (
. Opisany przebieg rozwiązań wiąże się z tym, że konkurencja zewnętrzna okazuje się znacznie bardziej niebezpieczna (![]() lub
lub ![]() ) dla jednego z gatunków, a mało wpływa na drugi. Wtedy ten, dla którego jest niebezpieczna — ginie.
) dla jednego z gatunków, a mało wpływa na drugi. Wtedy ten, dla którego jest niebezpieczna — ginie.
Jeśli oba parametry ![]() lub
lub ![]() , to nietrywialne izokliny przecinają się tworząc dodatni stan stacjonarny. Jeśli jednak oba parametry są powyżej
, to nietrywialne izokliny przecinają się tworząc dodatni stan stacjonarny. Jeśli jednak oba parametry są powyżej ![]() , stan ten jest siodłem, natomiast w przeciwnym przypadku — węzłem stabilnym. W przestrzeni fazowej
, stan ten jest siodłem, natomiast w przeciwnym przypadku — węzłem stabilnym. W przestrzeni fazowej ![]() możemy teraz wydzielić 4 obszary i analogicznie jak w przypadku 1., analizując przebieg pola wektorowego wnioskujemy, że w przypadku 3. dodatni stan stacjonarny jest globalnie stabilny we wnętrzu przestrzeni fazowej, natomiast w przypadku 2. rozmaitość stabilna tworzy separatrysę rozdzielającą baseny przyciągania stanów
możemy teraz wydzielić 4 obszary i analogicznie jak w przypadku 1., analizując przebieg pola wektorowego wnioskujemy, że w przypadku 3. dodatni stan stacjonarny jest globalnie stabilny we wnętrzu przestrzeni fazowej, natomiast w przypadku 2. rozmaitość stabilna tworzy separatrysę rozdzielającą baseny przyciągania stanów ![]() i
i ![]() — w zależności od warunku początkowego jeden gatunek przeżywa, a drugi ginie.
— w zależności od warunku początkowego jeden gatunek przeżywa, a drugi ginie.
Podsumowując przeprowadzoną analizę zauważmy, że jeśli tylko ![]() , co oznacza, że co najmniej jeden ze współczynników
, co oznacza, że co najmniej jeden ze współczynników ![]() ,
, ![]() przewyższa
przewyższa ![]() , to dynamika modelu odzwierciedla znaną zasadę ekologiczną mówiącą o konkurencyjnym wykluczaniu gatunków — jeśli nisze ekologiczne dwóch konkurujących gatunków zbytnio się pokrywają, to jeden z gatunków wypiera drugi. Tylko przy bardzo szczególnych układach parametrów możliwe jest współistnienie takich gatunków w tym samym siedlisku.
, to dynamika modelu odzwierciedla znaną zasadę ekologiczną mówiącą o konkurencyjnym wykluczaniu gatunków — jeśli nisze ekologiczne dwóch konkurujących gatunków zbytnio się pokrywają, to jeden z gatunków wypiera drugi. Tylko przy bardzo szczególnych układach parametrów możliwe jest współistnienie takich gatunków w tym samym siedlisku.
8.2. Modelowanie symbiozy
Kolejnym typem oddziaływań występujących między dwoma gatunkami
![]() ,
, ![]() jest symbioza.
Analogicznie jak w przypadku modelu konkurujących gatunków budując model heurystyczny zakładamy, że wewnętrzną dynamikę każdego z gatunków można opisać za pomocą modelu logistycznego, ze względu na ograniczoną pojemność środowiska, a co za tym idzie — występowanie konkurencji wewnątrzgatunkowej. Oddziaływania międzygatunkowe pojawiają się oczywiście wtedy, gdy spotykają się osobniki różnych gatunków i — ponownie podobnie do poprzednich przypadków — zakłada się, że wpływ tych oddziaływań na dynamikę każdego z gatunków zależy od liczby spotkań między osobnikami gatunków
jest symbioza.
Analogicznie jak w przypadku modelu konkurujących gatunków budując model heurystyczny zakładamy, że wewnętrzną dynamikę każdego z gatunków można opisać za pomocą modelu logistycznego, ze względu na ograniczoną pojemność środowiska, a co za tym idzie — występowanie konkurencji wewnątrzgatunkowej. Oddziaływania międzygatunkowe pojawiają się oczywiście wtedy, gdy spotykają się osobniki różnych gatunków i — ponownie podobnie do poprzednich przypadków — zakłada się, że wpływ tych oddziaływań na dynamikę każdego z gatunków zależy od liczby spotkań między osobnikami gatunków ![]() oraz
oraz ![]() .
.
Niech ![]() oznaczają liczbę osobników (zagęszczenia) gatunków
oznaczają liczbę osobników (zagęszczenia) gatunków ![]() ,
, ![]() . Układ symbiotyczny możemy opisać za pomocą następujących równań
. Układ symbiotyczny możemy opisać za pomocą następujących równań
![\begin{array}[]{lcl}\dot{N}_{1}&=&r_{1}N_{1}\left(1-\frac{N_{1}}{K_{1}}+b_{{12}}N_{2}\right),\\
\dot{N}_{2}&=&r_{2}N_{2}\left(1-\frac{N_{2}}{K_{2}}+b_{{21}}N_{1}\right),\end{array}](wyklady/mbm/mi/mi702.png) |
(8.3) |
gdzie tradycyjnie ![]() oznacza współczynnik rozrodczości gatunku
oznacza współczynnik rozrodczości gatunku ![]() , pojemności środowiska dla danego gatunku oznaczamy
, pojemności środowiska dla danego gatunku oznaczamy ![]() , natomiast
, natomiast ![]() opisuje siłę wpływu oddziaływań symbiotycznych dla gatunku
opisuje siłę wpływu oddziaływań symbiotycznych dla gatunku ![]() w symbiozie z gatunkiem
w symbiozie z gatunkiem ![]() .
.
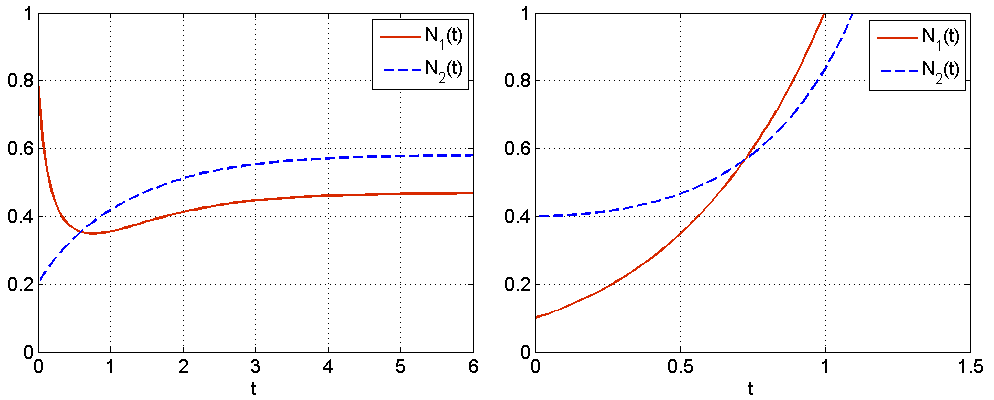
Zauważmy, że lokalne istnienie, jednoznaczność i nieujemność rozwiązań układu (8.3) dla nieujemnego warunku początkowego wykazujemy dość łatwo — stosując podobne argumenty jak w przypadku układu (8.1). Natomiast określoność rozwiązań dla wszystkich ![]() staje się tu własnością pożądaną, ale nie zawsze występującą. Rozpatrzmy następującą sytuację. Niech oba gatunki charakteryzują się tymi samymi parametrami,
staje się tu własnością pożądaną, ale nie zawsze występującą. Rozpatrzmy następującą sytuację. Niech oba gatunki charakteryzują się tymi samymi parametrami, ![]() ,
, ![]() i
i ![]() . Załóżmy też, że na początku liczebność obu gatunków jest jednakowa. Wobec tego, ze względu na całkowitą symetrię — liczebność tych gatunków jest jednakowa dla dowolnej chwili
. Załóżmy też, że na początku liczebność obu gatunków jest jednakowa. Wobec tego, ze względu na całkowitą symetrię — liczebność tych gatunków jest jednakowa dla dowolnej chwili ![]() , dla której istnieje rozwiązanie układu (8.3). Skoro
, dla której istnieje rozwiązanie układu (8.3). Skoro ![]() , to
, to
i jeśli ![]() , to
, to ![]() stale rośnie. Co więcej,
stale rośnie. Co więcej, ![]() , gdzie
, gdzie ![]() . Wiadomo natomiast, że rozwiązania równania
. Wiadomo natomiast, że rozwiązania równania ![]() dla dodatniego warunku początkowego
dla dodatniego warunku początkowego ![]() są określone w skończonym przedziale czasu
są określone w skończonym przedziale czasu ![]() , ponieważ dla
, ponieważ dla ![]() zachodzi
zachodzi ![]() .
Rzeczywiście, rozwiązując to równanie metodą rozdzielenia zmiennych dostajemy
.
Rzeczywiście, rozwiązując to równanie metodą rozdzielenia zmiennych dostajemy
![]() i dla
i dla ![]() mianownik rozwiązania zeruje się. Tego typu zachowania możemy się spodziewać za każdym razem, gdy w modelu występuje składnik kwadratowy z dodatnim współczynnikiem.
mianownik rozwiązania zeruje się. Tego typu zachowania możemy się spodziewać za każdym razem, gdy w modelu występuje składnik kwadratowy z dodatnim współczynnikiem.
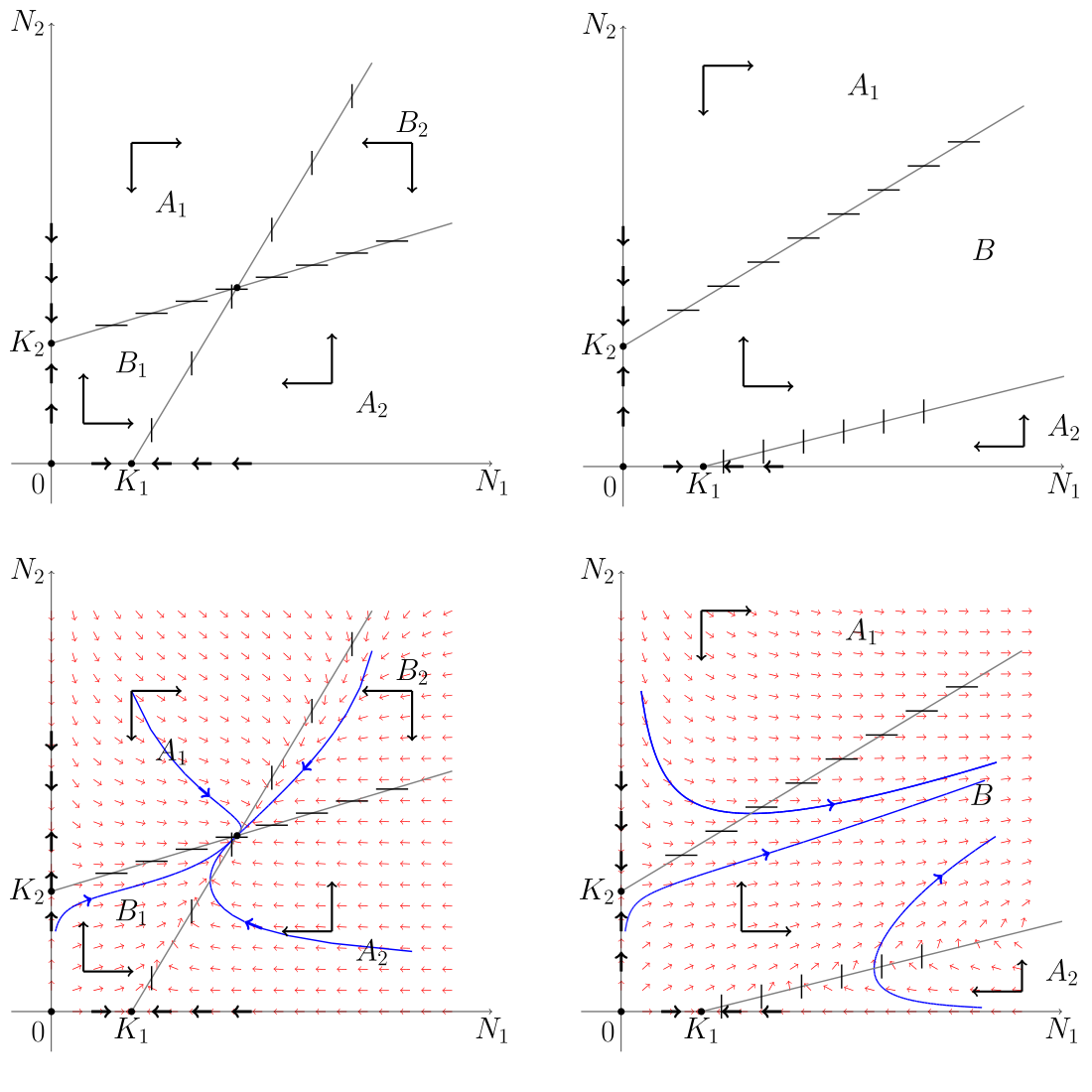
Przeprowadzimy teraz analizę portretu fazowego układu (8.3) w zależności od parametrów. Izokliny zerowe zadane są za pomocą następujących prostych
-
dla zmiennej
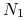 :
: 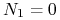 lub
lub 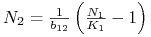 ;
; -
dla zmiennej
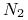 :
: 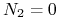 lub
lub 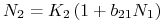 .
.
Widzimy więc, że niezerowe izokliny są prostymi o dodatnim współczynniku kierunkowym, zatem w zależności od parametrów mogą się przecinać lub nie w pierwszej ćwiartce ![]() , czyli naszej przestrzeni fazowej. Wobec tego układ ma albo 3 stany stacjonarne
, czyli naszej przestrzeni fazowej. Wobec tego układ ma albo 3 stany stacjonarne ![]() ,
, ![]() i
i ![]() , jeśli izokliny się nie przecinają, albo 4 takie stany, jeśli się przecinają i wtedy mamy dodatni stan stacjonarny
, jeśli izokliny się nie przecinają, albo 4 takie stany, jeśli się przecinają i wtedy mamy dodatni stan stacjonarny
Zauważmy, że stan ten istnieje przy założeniu ![]() , co w praktyce oznacza, że przy zadanych pojemnościach środowiska dla rozważanych gatunków zysk płynący z oddziaływań symbiotycznych nie może być zbyt duży, aby gatunki mogły pozostawać w pewnej równowadze, opisanej przez stan stacjonarny. W takim układzie mamy
, co w praktyce oznacza, że przy zadanych pojemnościach środowiska dla rozważanych gatunków zysk płynący z oddziaływań symbiotycznych nie może być zbyt duży, aby gatunki mogły pozostawać w pewnej równowadze, opisanej przez stan stacjonarny. W takim układzie mamy ![]() ,
, ![]() , czyli współrzędne dodatniego stanu stacjonarnego przewyższają pojemności środowiska.
, czyli współrzędne dodatniego stanu stacjonarnego przewyższają pojemności środowiska.
Wyznaczmy teraz wartości własne odpowiadające poszczególnym stanom stacjonarnym. Macierz Jacobiego układu (8.3) jest równa
![MJ(N_{1},N_{2})=\left(\begin{array}[]{cc}r_{1}\left(1-2\frac{N_{1}}{K_{1}}+b_{{12}}N_{2}\right)&r_{1}b_{{12}}N_{1}\\
r_{2}b_{{21}}N_{2}&r_{2}\left(1-2\frac{N_{2}}{K_{2}}+b_{{21}}N_{1}\right)\end{array}\right)](wyklady/mbm/mi/mi679.png) |
(8.4) |
Podstawiając do wzoru (8.4) współrzędne poszczególnych stanów stacjonarnych otrzymujemy wartości własne
-
dla
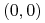 mamy
mamy 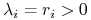 ,
, 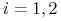 ;
; -
dla
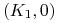 :
: 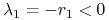 ,
, 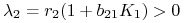 i symetrycznie dla
i symetrycznie dla 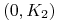 :
: 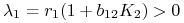 ,
, 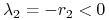 ;
;
-
dla
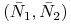 :
: 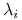 ,
, 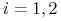 są rozwiązaniami równania charakterystycznego
są rozwiązaniami równania charakterystycznego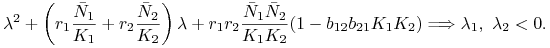
Wobec tego ![]() jest węzłem niestabilnym,
jest węzłem niestabilnym, ![]() i
i ![]() są siodłami, natomiast dodatni stan stacjonarny, jeśli istnieje, to jest węzłem stabilnym.
są siodłami, natomiast dodatni stan stacjonarny, jeśli istnieje, to jest węzłem stabilnym.
Na rysunku 8.3 widzimy przebieg pola wektorowego ![]() w obu przypadkach. Jeśli izokliny nie przecinają się w analizowanej przestrzeni fazowej, to łatwo możemy wywnioskować, że obie współrzędne rozwiązania są nieograniczone i albo są stale rosnące, albo na początku maleją osiągając w pewnej chwili
w obu przypadkach. Jeśli izokliny nie przecinają się w analizowanej przestrzeni fazowej, to łatwo możemy wywnioskować, że obie współrzędne rozwiązania są nieograniczone i albo są stale rosnące, albo na początku maleją osiągając w pewnej chwili ![]() minimum, a potem rosną dla
minimum, a potem rosną dla ![]() . Rzeczywiście, przestrzeń fazową możemy podzielić na trzy obszary, oznaczone na portrecie fazowym
. Rzeczywiście, przestrzeń fazową możemy podzielić na trzy obszary, oznaczone na portrecie fazowym ![]() (ponad izokliną zerową dla
(ponad izokliną zerową dla ![]() ),
), ![]() (pod izokliną zerową dla
(pod izokliną zerową dla ![]() ) i
) i ![]() (pomiędzy izoklinami). W obszarze
(pomiędzy izoklinami). W obszarze ![]() zmienna
zmienna ![]() maleje, a
maleje, a ![]() rośnie. Wewnątrz tego obszaru nie ma stanów stacjonarnych, a stan stacjonarny na brzegu jest siodłem, przy czym jego rozmaitość stabilna pokrywa się z osią
rośnie. Wewnątrz tego obszaru nie ma stanów stacjonarnych, a stan stacjonarny na brzegu jest siodłem, przy czym jego rozmaitość stabilna pokrywa się z osią ![]() , zatem rozwiązanie nie może zbiegać do tego stanu. Wnioskujemy więc, że rozwiązanie opuszcza ten obszar i przechodzi do obszaru
, zatem rozwiązanie nie może zbiegać do tego stanu. Wnioskujemy więc, że rozwiązanie opuszcza ten obszar i przechodzi do obszaru ![]() . Symetrycznie przebiegają orbity w obszarze
. Symetrycznie przebiegają orbity w obszarze ![]() , zatem także wchodzą do
, zatem także wchodzą do ![]() . Z kolei w
. Z kolei w ![]() obie zmienne są rosnące, przy czym rosną nieograniczenie — gdyby wzrost którejś z nich był ograniczony, to musiałaby być zbieżna, co oznacza, że pochodna też byłaby ograniczona, a nawet dążyłaby do
obie zmienne są rosnące, przy czym rosną nieograniczenie — gdyby wzrost którejś z nich był ograniczony, to musiałaby być zbieżna, co oznacza, że pochodna też byłaby ograniczona, a nawet dążyłaby do ![]() , co jest niemożliwe ze względu na przebieg pola wektorowego.
, co jest niemożliwe ze względu na przebieg pola wektorowego.
Wróćmy teraz do problemu określoności rozwiązań dla wszystkich ![]() . Zauważmy, że gdyby np. zmienna
. Zauważmy, że gdyby np. zmienna ![]() rosła do
rosła do ![]() w skończonym czasie, to oznaczałoby, że pewnej chwili musiałaby przeciąć izoklinę zerową zmiennej
w skończonym czasie, to oznaczałoby, że pewnej chwili musiałaby przeciąć izoklinę zerową zmiennej ![]() , co znów nie zgadza się z przebiegiem pola. Zatem obie zmienne są określone dla wszystkich
, co znów nie zgadza się z przebiegiem pola. Zatem obie zmienne są określone dla wszystkich ![]() i
i ![]() ,
, ![]() , oczywiście poza przypadkiem omówionym powyżej, gdy poszczególne współczynniki dla obu gatunków pokrywają się.
, oczywiście poza przypadkiem omówionym powyżej, gdy poszczególne współczynniki dla obu gatunków pokrywają się.
Jeśli izokliny zerowe przecinają się w pierwszej ćwiartce układu współrzędnych, to przestrzeń fazowa dzieli się na 4 obszary, ![]() — ponad obydwoma izoklinami,
— ponad obydwoma izoklinami, ![]() — pod nimi,
— pod nimi, ![]() i
i ![]() — pomiędzy nimi. W obszarze
— pomiędzy nimi. W obszarze ![]() obie zmienne rosną, natomiast w
obie zmienne rosną, natomiast w ![]() — obie maleją.
Zauważmy, że każdy prostokąt o jednym wierzchołku w początku układu współrzędnych i dwóch bokach wzdłuż osi oraz naprzeciwległym wierzchołku w obszarze
— obie maleją.
Zauważmy, że każdy prostokąt o jednym wierzchołku w początku układu współrzędnych i dwóch bokach wzdłuż osi oraz naprzeciwległym wierzchołku w obszarze ![]() jest zbiorem niezmienniczym, gdyż pole wektorowe wchodzi do wewnątrz. Wobec tego każde rozwiązanie pozostaje ograniczone i analizując pole wektorowe dochodzimy do wniosku, że każde rozwiązanie układu (8.3) z dodatnim warunkiem początkowym zbiega do punktu krytycznego
jest zbiorem niezmienniczym, gdyż pole wektorowe wchodzi do wewnątrz. Wobec tego każde rozwiązanie pozostaje ograniczone i analizując pole wektorowe dochodzimy do wniosku, że każde rozwiązanie układu (8.3) z dodatnim warunkiem początkowym zbiega do punktu krytycznego ![]() .
.
Zauważmy, że symbioza zawsze działa korzystnie na liczebność gatunków, które w taki sposób na siebie oddziałują, ale tylko w przypadku drugim, gdy efekt tych oddziaływań nie jest nadmierny, gatunki mogą współistnieć w środowisku. Natomiast jeśli oddziaływania symbiotyczne przekraczają pewien próg, to prowadzi do nieograniczonego wzrostu obu populacji, co oczywiście w warunkach rzeczywistych nie może mieć miejsca i musi zakończyć się katastrofą, por. rys. 8.4.