Zagadnienia
5. Symetria sferyczna w 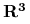
5.1. Pola centralne
Definicja 5.1
Polem centralnym w ![]() nazwiemy pole wektorowe
nazwiemy pole wektorowe ![]() na
na ![]() o postaci
o postaci
| (5.1) |
gdzie ![]() jest funkcją ciągłą a
jest funkcją ciągłą a ![]() Pole (5.1) jest zawsze potencjalne z potencjałem
Pole (5.1) jest zawsze potencjalne z potencjałem ![]() gdzie
gdzie ![]() jest funkcją pierwotną
jest funkcją pierwotną ![]() . (Porównaj dowód Swierdzenia 4.3.).
. (Porównaj dowód Swierdzenia 4.3.).
Definicja 5.2
Grupą ortogonalną ![]() nazwiemy grupę przekształceń liniowych, scharakteryzowanych warunkiem:
nazwiemy grupę przekształceń liniowych, scharakteryzowanych warunkiem: ![]() wtedy i tylko wtedy, kiedy
wtedy i tylko wtedy, kiedy
| (5.2) |
Warunek ten jest równoważny warunkowi podającemu opis macierzy przekształceń liniowych tworzących ![]()
![]() wtedy i tylko wtedy, kiedy macierz
wtedy i tylko wtedy, kiedy macierz ![]() tego przekształcenia względem dowolnej bazy ortonormalnej spełnia warunek
tego przekształcenia względem dowolnej bazy ortonormalnej spełnia warunek
| (5.3) |
gdzie ![]() oznacza macież transponowaną do
oznacza macież transponowaną do ![]()
Stwierdzenie 5.1
Pole centralne (5.1) jest niezmiennicze dla naturalnego działania w ![]() grupy przekształceń ortogonalnych
grupy przekształceń ortogonalnych ![]() Oznacza to, że dla każdego
Oznacza to, że dla każdego ![]() oraz dla każdego
oraz dla każdego ![]() zachodzi
zachodzi
| (5.4) |
Dla przekształcenia liniowego ![]() jego różniczka w dowolnym punkcie jest równa
jego różniczka w dowolnym punkcie jest równa ![]() Zatem z (5.1) dla
Zatem z (5.1) dla ![]() oraz
oraz ![]() wynika
wynika
Wykorzystaliśmy tu równość ![]() wynikającą z (5.2).
wynikającą z (5.2).
Stwierdzenie 5.2
Dla pola centralnego w ![]() moment pędu
moment pędu ![]() jest całką pierwszą.
jest całką pierwszą.
Niech ![]() będzie ruchem punktu o masie
będzie ruchem punktu o masie ![]() pod działaniem centralnej siły
pod działaniem centralnej siły ![]() Niech
Niech ![]() oznacza iloczyn wektorowy w
oznacza iloczyn wektorowy w ![]() Wtedy
Wtedy
bo wektor ![]() jest proporcjonalny do
jest proporcjonalny do ![]()
Wniosek 5.1
Ruch w polu centralnym w ![]() jest płaski. Dokładniej:
jest płaski. Dokładniej:
(A) Jeżeli ![]() to ruch odbywa się w płaszczyźnie.
to ruch odbywa się w płaszczyźnie.
| (5.5) |
którą też można opisać jako płaszczyznę rozpinaną przez ![]() oraz
oraz ![]()
(B) Jeżeli ![]() to ruch odbywa się po prostej zawierającej
to ruch odbywa się po prostej zawierającej ![]() oraz
oraz ![]()
(A) Ze stałości ![]() wynika, że
wynika, że ![]() Zatem
Zatem ![]() dla każdego
dla każdego ![]() . Ponadto
. Ponadto ![]() i
i ![]() należą do
należą do ![]() i nie są współliniowe.
i nie są współliniowe.
(B) Jeżeli ![]() to
to ![]() czyli
czyli
| (5.6) |
gdzie funkcja ![]() jest różniczkowalna ( bo
jest różniczkowalna ( bo ![]() ) jest dwukrotnie różniczkowalna). Niech
) jest dwukrotnie różniczkowalna). Niech ![]() będzie funkcją różniczkowalną. Wtedy funkcja wektorowa
będzie funkcją różniczkowalną. Wtedy funkcja wektorowa ![]() spełnia warunek
spełnia warunek
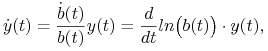 |
który dla ![]() przechodzi na (5.6). Z twierdzenia o jednoznaczności mamy więc
przechodzi na (5.6). Z twierdzenia o jednoznaczności mamy więc
Wniosek 5.2
Niech ![]() będzie polem centralnym w
będzie polem centralnym w ![]() a
a ![]() podprzestrzenią w
podprzestrzenią w ![]() rozpiętą przez dwie pierwsze osie współrzędnych.
Każdą trajektorię ruchu w polu
rozpiętą przez dwie pierwsze osie współrzędnych.
Każdą trajektorię ruchu w polu ![]() można uzyskać jako obraz pewnej trajektorii tego pola, leżącej w
można uzyskać jako obraz pewnej trajektorii tego pola, leżącej w ![]() za pomocą pewnego przekształcenia
za pomocą pewnego przekształcenia ![]()
Niech
będzie krzywą ruchu dla pola ![]() Rozpatrzmy przypadek kiedy
Rozpatrzmy przypadek kiedy
Przypadek ![]() zostawimy jako zadanie czytelnikowi.
zostawimy jako zadanie czytelnikowi.
Niech ![]() będzie takim przekształceniem ortogonalnym , że
będzie takim przekształceniem ortogonalnym , że
Wtedy ![]() (
(![]() jak w (5.5)).
Niech
jak w (5.5)).
Niech
i niech ![]() będzie krzywą ruchu w polu
będzie krzywą ruchu w polu ![]() wyznaczoną przez warunki początkowe
wyznaczoną przez warunki początkowe ![]() ,
,![]() Wtedy
Wtedy ![]() oraz
oraz ![]()
Wniosek 5.3
Każdy ruch w polu centralnym ![]() jest izometrycznie równoważny pewnemu ruchowi w polu centralnym w
jest izometrycznie równoważny pewnemu ruchowi w polu centralnym w ![]()
Każde pole centralne w ![]() powstaje przez ograniczenie do przestrzeni
powstaje przez ograniczenie do przestrzeni ![]() pewnego pola centralnego w
pewnego pola centralnego w ![]() - i odwrotnie - każde takie pole jest wyznaczone przez swoje ograniczenie do
- i odwrotnie - każde takie pole jest wyznaczone przez swoje ograniczenie do ![]()
5.2. Ruch w polu centralnym w 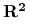
Zaczniemy od sformułowania analogii Stwierdzenia 5.2 dla ruchu w centralnym polu w ![]() Dla uproszczenia, w dalszej części tego punktu przyjmiemy, że
Dla uproszczenia, w dalszej części tego punktu przyjmiemy, że ![]() Zanurzając
Zanurzając ![]() jako przestrzeń
jako przestrzeń ![]() w
w ![]() rozważmy ruch
rozważmy ruch ![]() w
w ![]() Wtedy
Wtedy
Zatem funkcja
| (5.7) |
jest (skalarną) całką pierwszą ruchu w polu centralnym w ![]() Nadamy tej funkcji sens geometryczny, przechodząc do współrzędnych biegunowych
Nadamy tej funkcji sens geometryczny, przechodząc do współrzędnych biegunowych ![]() Wtedy
Wtedy
a zatem
Stwierdzenie 5.3
Dla ruchu w polu centralnym w ![]() opisanym za pomocą współrzędnych biegunowych zachodzi
opisanym za pomocą współrzędnych biegunowych zachodzi
| (5.9) |
gdzie
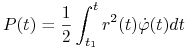 |
(5.10) |
oznacza pole sektora ograniczonego promieniami ![]() oraz krzywą ruchu
oraz krzywą ruchu ![]() Wielkość
Wielkość ![]() nazywamy prędkością polową.
nazywamy prędkością polową.
Ponieważ w przypadku koła o promieniu r pole wycinka kołowego opartego na łuku o kącie środkowym ![]() wynosi
wynosi
to pole sektora krzywoliniowego ograniczonego promieniami ![]() i
i ![]() oraz krzywą
oraz krzywą ![]() otrzymamy jako
otrzymamy jako
| (5.11) |
Zakładamy, że funkcja ![]() jest ciągła na przedziale
jest ciągła na przedziale ![]() Jeżeli zarówno
Jeżeli zarówno ![]() jak
jak ![]() są funkcjami
są funkcjami ![]() i przy tym
i przy tym ![]() jest monotoniczna,
jest monotoniczna, ![]() przechodzi na (5.10) i wtedy
przechodzi na (5.10) i wtedy
Wniosek 5.4
Ruch w polu centralnym w ![]() odbywa się w płaszczyźnie w taki sposób, że jego prędkość polowa względem centrum jest stała.
odbywa się w płaszczyźnie w taki sposób, że jego prędkość polowa względem centrum jest stała.
Reguła ta została doświadczalnie wykryta przez Keplera dla ruchu Marsa wokół Słońca.
5.3. Całkowanie równań ruchu w polu centralnym w 
Ponieważ siła w polu centralnym w każdym punkcie jest skierowana radialnie, wygodnie będzie opisywać ruch, rozkładając w każdej chwili występujące wektory względem zmiennego układu ortogonalnego ![]() w taki sposób ,że dla punktu o współrzędnych biegunowych
w taki sposób ,że dla punktu o współrzędnych biegunowych ![]() stosowany w chwli t
układ będzie miał postać:
stosowany w chwli t
układ będzie miał postać:
Ostrzeżenie Obserwowana poprzez liczenie pochodnych zmiana w czasie dotyczy układu nieruchomego i te pochodne dopiero po ich policzeniu rozkładamy względem zmieniającej się w czasie bazy.
Zaczniemy od obliczenia pochodnych funkcji ![]() i
i ![]() i przedstawieniu ich w układzie ruchomym. I tak
i przedstawieniu ich w układzie ruchomym. I tak
| (5.12) |
(W dalszym ciągu dla większej przejrzystości długich wzorów zrezygnujemy z pisania explicite argumentu ![]() Zatem napiszemy
Zatem napiszemy ![]() zamiast
zamiast ![]() , podobnie
, podobnie ![]() zamiast
zamiast ![]() i tak dalej.)
i tak dalej.)
Ponieważ ![]() otrzymamy stąd dwa równania
otrzymamy stąd dwa równania
| (5.13) |
Zauważmy, że zasada stałości prędkości polowej oznacza, że
| (5.14) |
czyli
a zatem drugie z równań (5.13) jest równoważne warunkowi (5.14), który jest równoważny równości ![]()
![]() jest stałą zależną od warunków początkowych, którą dla zwięzłości nazwiemy momentem pędu. Zatem
jest stałą zależną od warunków początkowych, którą dla zwięzłości nazwiemy momentem pędu. Zatem
| (5.15) |
Wstawiając (5.15) do pierwszego z równań (5.13) sprowadzamy je do postaci zawierającej tylko funkcję ![]() i jej pochodne:
i jej pochodne:
| (5.16) |
Podsumujemy nasze rozważania tak:
Stwierdzenie 5.4
Odległość od środka układu w ruchu centralnym w ![]() z momentem pędu
z momentem pędu ![]() i potencjałem
i potencjałem ![]() zmienia się jak odległość od zera w jednowymiarowym ruchu z potencjałem
zmienia się jak odległość od zera w jednowymiarowym ruchu z potencjałem
| (5.17) |
Istotnie, możemy przepisać (5.16) w postaci
| (5.18) |
Stwierdzenie 5.5
Energia całkowita w ruchu dwuwymiarowym z ustalonym momentem pędu ![]() jest taka sama, jak dla ruchu jednowymiarowego z potencjałem (5.17).
jest taka sama, jak dla ruchu jednowymiarowego z potencjałem (5.17).
W ruchu z potencjałem (5.17) otrzymamy
| (5.19) |
natomiast w ruchu dwuwymiarowym, kiedy
![]() mamy
mamy ![]() a więc dla
a więc dla ![]() otrzymamy energię kinetyczną w postaci
otrzymamy energię kinetyczną w postaci
Aby podać explicite rozwiązanie równań (5.13) posłużymy się jeszcze jedną całką prostą, jaką jest energia całkowita (5.19).
Z (5.19) wynika, że przy ustalonych energii całkowitej ![]() oraz momencie pędu
oraz momencie pędu ![]() mamy
mamy
skąd
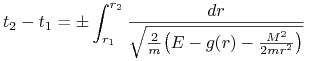 |
(5.20) |
Chcąc znależć postać ![]() zauważmy, że ze związku
zauważmy, że ze związku ![]() wynika, że
wynika, że ![]() jest ustalonego znaku a więc
jest ustalonego znaku a więc ![]() jest monotoniczną funkcją
jest monotoniczną funkcją ![]() i ma funkcję odwrotną
i ma funkcję odwrotną ![]() Wobec tego
Wobec tego ![]() z zatem
z zatem
Podstawiając tu ![]() oraz
oraz ![]() otrzymamy
otrzymamy
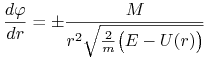 |
skąd
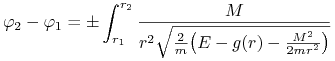 |




