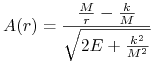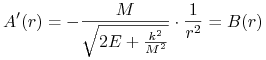6. Ruch w polu potencjału grawitacyjnego w 
6.1. Całkowanie równań ruchu
Jak zauważyliśmy w Przykładzie 1.2 siła z jaką Ziemia przyciąga małe obiekty jest w przybliżeniu odwrotnie proporcjonalna do kwadratu ich odległości od środka Ziemi.
Występujący we wzorze iloczyn masy Ziemi i masy przyciąganego przez nią obiektu zastąpimy dodatnim współczynnikiem ![]() Sytuacja ruchu takiego obiektu w polu grawitacyjnym Ziemi odpowada ruchowi w centralnym polu w
Sytuacja ruchu takiego obiektu w polu grawitacyjnym Ziemi odpowada ruchowi w centralnym polu w ![]() z potencjałem
z potencjałem
Zgodnie z rozważaniami z poprzedniego wykładu, podczas ruchu ciała o (stałym) momencie pędu ![]() w centralnym polu w
w centralnym polu w ![]() odległość
odległość ![]() ciała od centrum zmienia się tak, jak w jednowymiarowym ruchu z potencjałem zredukowanym
ciała od centrum zmienia się tak, jak w jednowymiarowym ruchu z potencjałem zredukowanym
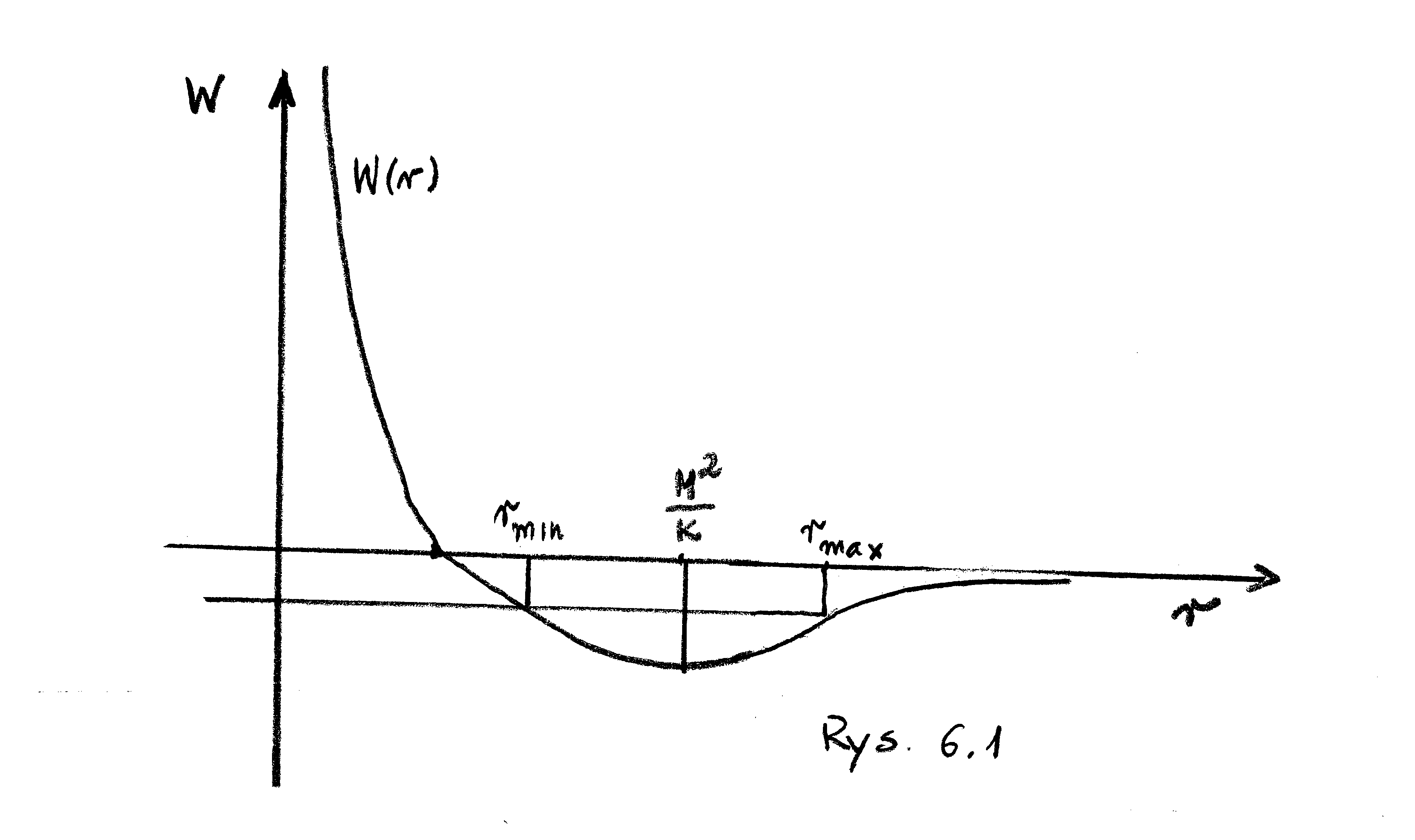
Wykres tego potencjału ma postać:
Ze Stwierdzenia 5.5 wiemy, że stała energia całkowita wynosi ![]() a więc
a więc
| (6.1) |
Z (6.1) wynika, że dla jakiegokolwiek ruchu musi być ![]() a zatem
a zatem ![]() Kształt wykresu
Kształt wykresu ![]() pokazuje, że ostatni warunek przy
pokazuje, że ostatni warunek przy ![]() zachodzi dla
zachodzi dla ![]() stanowiących półoś
stanowiących półoś ![]() natomiast
natomiast ![]() zachodzi dla
zachodzi dla ![]() z przedziałem
z przedziałem ![]()
Wyprzedzając ilościowy opis, który nastąpi, powiemy, że dla ![]() mamy do czynienia z sytuacją, kiedy nadlatujący z kosmosu obiekt ma zbyt dużą energię żeby zostać ”uwięziony” w roli satelity, jego tor ulega tylko zakrzywieniu i odlatuje z powrotem w kosmos.
mamy do czynienia z sytuacją, kiedy nadlatujący z kosmosu obiekt ma zbyt dużą energię żeby zostać ”uwięziony” w roli satelity, jego tor ulega tylko zakrzywieniu i odlatuje z powrotem w kosmos.
Przypadkowi ![]() odpowiada okresowy ruch po orbicie wokół centrum.
W każdej z dwóch powyższych sytuacji interesują nas jedynie wartości
odpowiada okresowy ruch po orbicie wokół centrum.
W każdej z dwóch powyższych sytuacji interesują nas jedynie wartości ![]() , przy których zachodzi (6.1), zatem otrzymamy wtedy
, przy których zachodzi (6.1), zatem otrzymamy wtedy
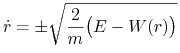 |
(6.2) |
przy czym znak ” + ” dotyczy części trajektorii, kiedy ![]() a znak ” - ” ma zastosowanie, kiedy
a znak ” - ” ma zastosowanie, kiedy ![]() maleje, czyli obiekt zbliża się do centrum. Jak pokazaliśmy (6.2) daje po rozwiązaniu zależność pomiędzy kątem
maleje, czyli obiekt zbliża się do centrum. Jak pokazaliśmy (6.2) daje po rozwiązaniu zależność pomiędzy kątem ![]() a promieniem
a promieniem ![]() we współrzędnych biegunowych w postaci
we współrzędnych biegunowych w postaci
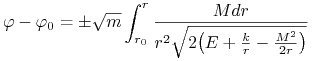 |
(6.3) |
Zwróćmy uwagę, że powyższy wzór odpowiada przyjętym dla ![]() i dla
i dla ![]() jednostkomi. Zmieniając je np. tylko dla
jednostkomi. Zmieniając je np. tylko dla ![]() możemy zlikwidować czynnik liczbowy, pojawiający się po prawej stronie równości (6.3).
możemy zlikwidować czynnik liczbowy, pojawiający się po prawej stronie równości (6.3).
Oznaczając funkcję pierwotną funkcji podcałkowej w (6.3) przez ![]() możemy też przyjąć
możemy też przyjąć ![]() co doprowadzi do wzoru
co doprowadzi do wzoru ![]() Aby znależć tę funkcję pierwotną przekształcimy funkcję podcałkową do postaci:
Aby znależć tę funkcję pierwotną przekształcimy funkcję podcałkową do postaci:
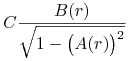 |
(6.4) |
gdzie ![]() a
a ![]() jest stałą ujemną.
jest stałą ujemną.
Ponieważ ![]() otrzymamy w rezultacie
otrzymamy w rezultacie
| (6.5) |
Sprowadzimy funkcję podcałkową do postaci jak w (6.4).Zauważmy, że
![2E+\frac{2k}{r}-\frac{M^{2}}{r^{2}}=\Bigg[-\Big(\frac{M}{r}-\frac{k}{M}\Big)^{2}+\Big(2E+\frac{k^{2}}{M^{2}}\Big)\Bigg]=](wyklady/mmk/mi/mi533.png) |
W postępowaniu powyższym jest luka polegająca na braku informacji,
że ![]() , co uniemożliwia napisanie potrzebnych formuł.
Jeżeli
, co uniemożliwia napisanie potrzebnych formuł.
Jeżeli ![]() sprawa jest oczywista. Jeżeli
sprawa jest oczywista. Jeżeli ![]() , to z (6.1) wynika, że
, to z (6.1) wynika, że
a więc ![]() W przypadku
W przypadku ![]() ostatnia nierówność może zajść jedynie, kiedy wyróżnik
ostatnia nierówność może zajść jedynie, kiedy wyróżnik ![]() jest nieujemny, co jest równoważne z warunkiem, że
jest nieujemny, co jest równoważne z warunkiem, że ![]()
6.2. Geometryczny opis trajektorii.
Przeskalowując ![]() możemy uzyskać opis trajektorii ruchu w postaci związku
możemy uzyskać opis trajektorii ruchu w postaci związku
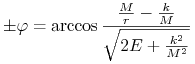 |
(6.6) |
Przekształcając równocześnie licznik i mianownik argumentu funkcji ![]()
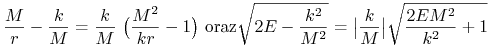 |
i upraszczając, otrzymamy
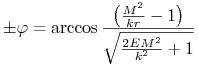 |
(6.7) |
Uproszczenie ![]() z
z ![]() w przypadku ujemnej wartości
w przypadku ujemnej wartości ![]() zmienia znak argumentu
zmienia znak argumentu ![]() Ponieważ
Ponieważ ![]() uzyskujemy (6.7) po następnym przeskalowaniu i zmianie zwrotu na osi
uzyskujemy (6.7) po następnym przeskalowaniu i zmianie zwrotu na osi ![]()
Wprowadźmy oznaczenia
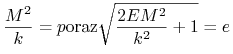 |
otrzymamy
| (6.8) |
skąd, z uwagi na parzystość funkcji ![]()
| (6.9) |
lub inaczej
| (6.10) |
Zauważmy ( porównaj wyjaśnienie kończące punkt 6.1), że 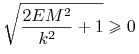 i dla
i dla ![]() otrzymamy
otrzymamy ![]() natomiast dla
natomiast dla ![]() jest
jest ![]()
Stwierdzenie 6.1
Zbiór punktów płaszczyzny, których współrzędne ![]() spełniają związek (6.10) może być również zdefiniowany następującym warunkiem geometrycznym.
spełniają związek (6.10) może być również zdefiniowany następującym warunkiem geometrycznym.
Warunek.
Stosunek odległości punktu od zera do odległości punktu od prostej ![]() (prostą tę nazywamy kierownicą) jest stały i wynosi
(prostą tę nazywamy kierownicą) jest stały i wynosi ![]()
Dla punktu ![]() na płaszczyźnie jego odległość od zera wynosi
na płaszczyźnie jego odległość od zera wynosi ![]() natomiast odległość od kierownicy wynonosi
natomiast odległość od kierownicy wynonosi ![]() , zatem nasz warunek brzmi:
, zatem nasz warunek brzmi:
co po łatwych przekształceniach prowadzi do (6.10).
∎Specjalne położenie krzywej opisanej równaniem (6.10) w stosunku do kartezjańskiego układu współrzędnych, jest związane z dokonanym (implicite) obrotem układu współrzędnych, który nastąpił przy afinicznym przekształcaniu kąta ![]() wykonanym przy całkowaniu funkcji (6.6).
wykonanym przy całkowaniu funkcji (6.6).
Dalsza część naszych rozważań dotyczy geometrycznej definicji stożkowych i jest z konieczności nieco szkicowa. Jej celem jest pokazanie w przypadku elips równoważności następującej dalej definicji geometrycznej (6.7), opisu (6.10) i opisu za pomocą równania osiowego dla elips.
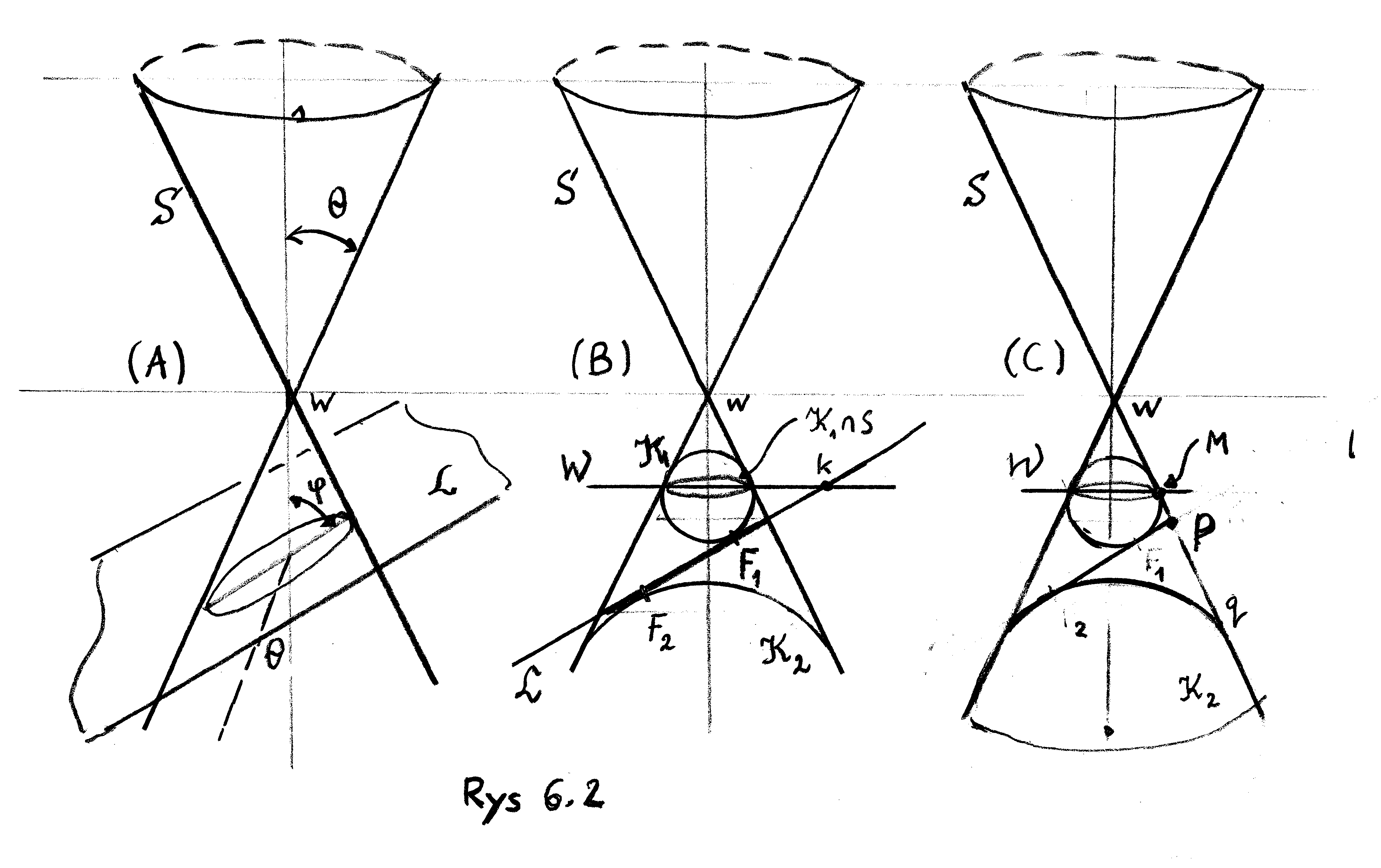
Rozważmy stożek ![]() w przestrzeni
w przestrzeni ![]() z wierzchołkiem
z wierzchołkiem ![]() i osią
i osią ![]() (zob. rys 6.2 (A).
(zob. rys 6.2 (A).
Przekrójmy stożek ![]() płaszczyzną
płaszczyzną ![]() . Niech
. Niech ![]() będzie połową kąta rozwarcia stożka a
będzie połową kąta rozwarcia stożka a ![]() kątem, jaki tworzy płaszczyzna
kątem, jaki tworzy płaszczyzna ![]() z osią stożka
z osią stożka ![]()
Definicja 6.1
Krzywą przecięcia stożka z płaszczyzną nazwiemy
(a) elipsą, jeżeli ![]()
(b) parabolą, jeżeli ![]()
(c) hiperbolą, jeżeli ![]()
Stwierdzenie 6.2
Niech ![]() będzie elipsą w sensie Definicji 6.1, wyznaczoną przez płaszczyznę
będzie elipsą w sensie Definicji 6.1, wyznaczoną przez płaszczyznę ![]() Istnieją na płaszczyźnie
Istnieją na płaszczyźnie ![]() punkt
punkt ![]() i prosta
i prosta ![]() takie, że dla dowolnego
takie, że dla dowolnego ![]() zachodzi
zachodzi
gdzie ![]() i
i ![]() są kątami, jak w Definicji 6.1 a
są kątami, jak w Definicji 6.1 a ![]() (P, k) jest odległością punktu
(P, k) jest odległością punktu ![]() od prostej
od prostej ![]()
Określimy najpierw punkt ![]() i prostą
i prostą ![]() Niech
Niech ![]() i
i ![]() będą kulami stycznymi do stożka i do płaszczyzny
będą kulami stycznymi do stożka i do płaszczyzny ![]() (zob. rys. 6.2 (B)). Jako punkt
(zob. rys. 6.2 (B)). Jako punkt ![]() przyjmiemy punkt
przyjmiemy punkt ![]() a jako prostą
a jako prostą ![]() przecięcie
przecięcie ![]() z płaszczyzną
z płaszczyzną ![]() zawierającą
zawierającą ![]() i prostopadłą do osi stożka
i prostopadłą do osi stożka ![]() Poprowadźmy płaszczyznę
Poprowadźmy płaszczyznę ![]() (płaszczyzna rysunku 6.2(C))przez oś stożka
(płaszczyzna rysunku 6.2(C))przez oś stożka ![]() i dowolny ustalony punkt
i dowolny ustalony punkt ![]() , leżący na elipsie
, leżący na elipsie ![]() Niech q będzie tworzącą stożka, przechodzącą przez
Niech q będzie tworzącą stożka, przechodzącą przez ![]() i niech
i niech ![]() Niech wreszcie
Niech wreszcie ![]() będzie punktem na kierownicy k najbliższym
będzie punktem na kierownicy k najbliższym ![]() Wtedy rzuty prostopadłe odcinków
Wtedy rzuty prostopadłe odcinków ![]() i
i ![]() na oś stożka są takie same. Istotnie,
na oś stożka są takie same. Istotnie, ![]() i
i ![]() leżą na płaszczyźnie
leżą na płaszczyźnie ![]() prostopadłej do osi.
Poza tym
prostopadłej do osi.
Poza tym ![]() tworzy z osią
tworzy z osią ![]() kąt
kąt ![]() a odcinek
a odcinek ![]() kąt
kąt ![]() a długości odcinków
a długości odcinków ![]() i
i ![]() są równe. Zatem
są równe. Zatem
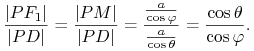 |
Stwierdzenie 6.3
Dla danej prostej ![]() i danego punktu
i danego punktu ![]() na płaszczyźnie zbiór punktów zdefiniowany warunkiem
na płaszczyźnie zbiór punktów zdefiniowany warunkiem ![]() jest izometryczny z elipsą w sensie Definicji 6.1.
jest izometryczny z elipsą w sensie Definicji 6.1.
(Szkic ).
Prowadząc przez ![]() prostą prostopadłą do
prostą prostopadłą do ![]() możemy znaleźć na niej punkt
możemy znaleźć na niej punkt ![]() tak, że
tak, że
![]() (
(![]() jest przecięciem
jest przecięciem ![]() z prostą prostopadłą).
Następnie rozpatrując przecięcie stożka płaszczyzną zawierającą oś stożka oraz punkty styczności kul
z prostą prostopadłą).
Następnie rozpatrując przecięcie stożka płaszczyzną zawierającą oś stożka oraz punkty styczności kul ![]() i
i ![]() z
z ![]() oraz rozpatrując rodzinę płaszczyzn równoległych, dla których
oraz rozpatrując rodzinę płaszczyzn równoległych, dla których ![]() , znajdujemy elipsę, o której należy pokazać, że jest izometryczna z naszą elipsą.
, znajdujemy elipsę, o której należy pokazać, że jest izometryczna z naszą elipsą.
6.3. Prawa Keplera
Około 1609 roku J. Kepler sformułował trzy prawa dotyczące ruchu planet wokół Słońca. Podamy ich współczesne sformułowanie.
I. Planety krążą wokół Słońca po elipsach, w których ognisku znajduje się Słońce.
II. W ruchu każdej planety prędkość polowa w płaszczyźnie ruchu pozostaje stała.
III. Dla dowolnych dwóch planet stosunek drugiej potęgi ich okresów obiegu jest równy stosunkowi trzecich potęg długości ich długich półosi.
Prawo pierwsze pokazaliśmy w poprzednim punkcie.
Prawo drugie jest prawdziwe dla dowolnego ruchu w polu centralnym.
Pokażemy, że zachodzi trzecie prawo Keplera.
Dowód trzeciego prawa Keplera.
Nietrudne, lecz kłopotliwe rachunki pozwalają przekonać się, że krzywa opisana w układzie biegunowym równaniem ![]() w układzie kartezjańskim ze środkiem w punkcie
w układzie kartezjańskim ze środkiem w punkcie ![]() jest przedstawiona równaniem
jest przedstawiona równaniem
![]() , gdzie
, gdzie ![]() są długościami wielkiej i małej półosi.
są długościami wielkiej i małej półosi.
Niech ![]() będzie okresem obiegu po takiej eliptycznej orbicie. Ze stałości prędkości polowej
będzie okresem obiegu po takiej eliptycznej orbicie. Ze stałości prędkości polowej ![]() mamy
mamy ![]() i podstawiając tu wartości na
i podstawiając tu wartości na ![]() i
i ![]() otrzymamy:
otrzymamy:
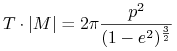 |
Podstawiając tu ![]() i
i 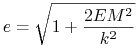 otrzymamy
otrzymamy
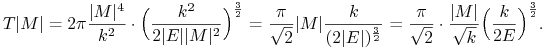 |
(6.11) |
Zauważmy teraz, że
wobec tego otrzymujemy
![=\Big(2E+\frac{k^{2}}{M^{2}}\Big)\Bigg[1-\Big(\frac{\frac{M}{r}-\frac{k}{M}}{\sqrt{\big(2E+\frac{k^{2}}{M^{2}}\big)}}\Big)^{2}\Bigg]](wyklady/mmk/mi/mi591.png)