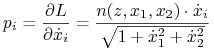Zagadnienia
9. Metoda Hamiltona w optyce geometrycznej
W roku 1828 William Rowan Hamilton opublikował fundamentalną pracę nadającą optyce geometrycznej nowe nieoczekiwane sformułowanie związane z geometrią symplektyczną. Poprzednio bieg promieni świetlnych opisywany był za pomocą równań Eulera, wynikających z wariacyjnej zasady minimalizującej ”długość optyczną” przebywanej drogi. Dopiero 20 lat później zauważył Hamilton, że to samo postępowanie, wykorzystujące tym razem wariacyjną zasadę najmniejszego działania, umożliwia także w mechanice uzyskanie nowego, znacznie bardziej geometrycznego opisu, niż ten, za pomocą równań Eulera - Legendre'a. Postępując za Hamiltonem, omówimy kolejno transformację Legendre'a - kluczowe narzędzie w metodzie Hamiltona. Następnie pokażemy, jak uzyskuje się za jej pomocą nowy opis w optyce geometrycznej. Na koniec wrócimy do mechaniki.
9.1. Transformacja Legendre'a
W całym tym paragrafie dla przestrzeni liniowej ![]() przez
przez ![]() będziemy oznaczać przestrzeń form liniowych na
będziemy oznaczać przestrzeń form liniowych na ![]() Zaczniemy od sytuacji jednowymiarowej. Niech
Zaczniemy od sytuacji jednowymiarowej. Niech ![]() będzie dwukrotnie różniczkowalna i niech
będzie dwukrotnie różniczkowalna i niech ![]() na
na ![]() Rozważmy przekształcenie
Rozważmy przekształcenie
Ponieważ ![]() jest ciągła i rosnąca, obrazem
jest ciągła i rosnąca, obrazem ![]() na mocy własności Darboux jest przedział
na mocy własności Darboux jest przedział ![]() oraz na
oraz na ![]() jest określone przekształcenie
jest określone przekształcenie ![]() odwrotne do
odwrotne do ![]()
Stwierdzenie 9.1
Istnieje ![]() taka, że
taka, że ![]() dla
dla ![]() [f'(a), f'(b)]. Funkcję
[f'(a), f'(b)]. Funkcję ![]() nazwiemy transformatą Legendre`a funkcji
nazwiemy transformatą Legendre`a funkcji ![]() i napiszemy
i napiszemy ![]() .
.
Stwierdzenie 9.2
Ponieważ funkcja ![]() i
i ![]() są obecne w naszych rozważaniach jedynie za pośrednictwem swoich pochodnych, obie są wyznaczone z dokładnością do stałej. Wygodnie będzie więc przyjąć umowę, że
są obecne w naszych rozważaniach jedynie za pośrednictwem swoich pochodnych, obie są wyznaczone z dokładnością do stałej. Wygodnie będzie więc przyjąć umowę, że ![]()
Dla ![]() rozważmy funkcję
rozważmy funkcję
| (9.1) |
Ustalając ![]() oznaczmy
oznaczmy ![]() Wtedy
Wtedy ![]() a ponieważ
a ponieważ ![]() oraz
oraz ![]() jest malejąca i ciągła, istnieje dokładnie jeden punkt
jest malejąca i ciągła, istnieje dokładnie jeden punkt ![]() taki, że
taki, że ![]() tj. że
tj. że ![]() Przekształcenie
Przekształcenie
jest oczywiście odwrotne do
i jako odwrotne do różniczkowalnego o niezerowej pochodnej, samo jest różniczkowalne.Podamy jego opis analityczny.
Określmy
| (9.2) |
wtedy
jest różniczkowalne oraz
bo ![]()
Wniosek 9.1
Transformacja Legendre'a jest inwolucją t.j. ![]()
Wyznaczyć transformatę Legendre'a następujących funkcji:
![]()
![]()
i wobec tego
wobec tego
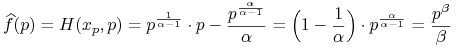 |
gdzie ![]()
Stwierdzenie 9.3
(Nierówność Younga ). Niech ![]() wtedy
wtedy
| (9.3) |
Sytuacja n-wymiarowa.
W następującym tekście przyjmiemy konwencję, że wartość różniczki funkcji ![]() w punkcie
w punkcie ![]() na wektorze
na wektorze ![]() jest zapisywana jako
jest zapisywana jako ![]() Niech
Niech ![]() bedzie określona i ma ciągłe pochodne do rzędu 2 na otwartym zbiorze
bedzie określona i ma ciągłe pochodne do rzędu 2 na otwartym zbiorze ![]() Niech ponadto
Niech ponadto ![]() dla
dla ![]() Przyjmujemy tutaj podejście wiążące kolejne różniczki ze wzorem Taylora i traktujące
Przyjmujemy tutaj podejście wiążące kolejne różniczki ze wzorem Taylora i traktujące ![]() jako odwzorowanie n- liniowe tam występujące. W szczególności
jako odwzorowanie n- liniowe tam występujące. W szczególności
| (9.4) |
oznacza wtedy macierz formy kwadratowej a napis ![]() oznacza, że forma ta jest dodatnio określona.
Rozważmy przekształcenie:
oznacza, że forma ta jest dodatnio określona.
Rozważmy przekształcenie: ![]()
Stwierdzenie 9.4
Jeżeli ![]() jest otwarty a
jest otwarty a ![]() jest klasy
jest klasy ![]() oraz
oraz ![]() dla
dla ![]() to także zbiór
to także zbiór ![]() jest otwarty.
jest otwarty.
Różniczka ![]() może być także interpretowana jako pierwsza różniczka w punkcie
może być także interpretowana jako pierwsza różniczka w punkcie ![]() odwzorowania
odwzorowania ![]() Ponieważ warunek
Ponieważ warunek ![]() implikuje, że macierz
implikuje, że macierz ![]() jest nieosobliwa, odwzorowanie
jest nieosobliwa, odwzorowanie ![]() jest otwarte i w szczególności
jest otwarte i w szczególności ![]() jest zbiorem otwartym.
jest zbiorem otwartym.
Stwierdzenie 9.5
Przy założeniach i notacji Stwierdzenia 9.4. przekształcenie ![]() jest różnowartościowe. Przekształcenie do niego odwrotne jest podobnej postaci t.j. przy kanonicznym utożsamieniu
jest różnowartościowe. Przekształcenie do niego odwrotne jest podobnej postaci t.j. przy kanonicznym utożsamieniu ![]() z
z ![]() i traktowaniu
i traktowaniu ![]() jako podzbioru
jako podzbioru ![]() istnieje funkcja
istnieje funkcja ![]() taka, że
taka, że ![]()
Funkcję ![]() nazywamy transformatą Legendre'a funkcji
nazywamy transformatą Legendre'a funkcji ![]()
Pokażemy najpierw, że funkcja ![]() jest różnowartościowa. Niech
jest różnowartościowa. Niech ![]() i niech
i niech ![]() Wtedy
Wtedy ![]() jest równa wartości formy kwadratowej
jest równa wartości formy kwadratowej ![]() na argumencie
na argumencie ![]() a zatem jest dodatnia. Oznacza to, że funkcja
a zatem jest dodatnia. Oznacza to, że funkcja ![]() jest rosnąca. Ale
jest rosnąca. Ale ![]() natomiast
natomiast ![]() a ponieważ
a ponieważ ![]() zatem
zatem ![]()
Pokażemy następnie, że istnieje ![]() klasy
klasy ![]() taka, że
taka, że ![]() oraz, że
oraz, że ![]()
Rozumowanie przebiega podobnie, jak w dowodzie Stwierdzenia 9.4.
Dla ![]() x
x ![]() rozważamy funkcję
rozważamy funkcję
gdzie ![]() oznacza wartość formy liniowej
oznacza wartość formy liniowej ![]() na wektorze
na wektorze ![]() W części pierwszej tego dowodu pokazaliśmy, że dla każdego
W części pierwszej tego dowodu pokazaliśmy, że dla każdego ![]() istnieje dokładnie jeden
istnieje dokładnie jeden ![]() taki, że
taki, że ![]() Określmy
Określmy
wtedy odworowanie ![]() jako odwrotne do
jako odwrotne do ![]() ma wszędzie różniczkę nieosobliwą na mocy twierdzenia o funkcji odwrotnej.
Pisząc
ma wszędzie różniczkę nieosobliwą na mocy twierdzenia o funkcji odwrotnej.
Pisząc ![]() i uwzględniając, że
i uwzględniając, że ![]() mamy wtedy
mamy wtedy
co należało wykazać.
Pokażemy wreszcie, że ![]()
Traktując ![]() jako różniczkę odwzorowania
jako różniczkę odwzorowania ![]() odwrotnego do
odwrotnego do ![]() którego różniczką jest
którego różniczką jest ![]() widzimy, że teza wynika z obserwacji, że dla macierzy symetrycznej i dodatnio określonej, macierz odwrotna jest także symetryczna i dodatnio określona.
widzimy, że teza wynika z obserwacji, że dla macierzy symetrycznej i dodatnio określonej, macierz odwrotna jest także symetryczna i dodatnio określona.
Ćwiczenie 9.1
Wyznaczyć transformatę Legendre'a funkcji:
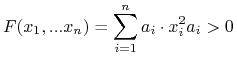 |
wtedy
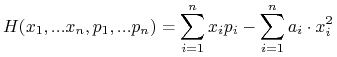 |
i otrzymujemy
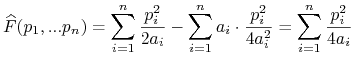 |
9.2. Optyka geometryczna.
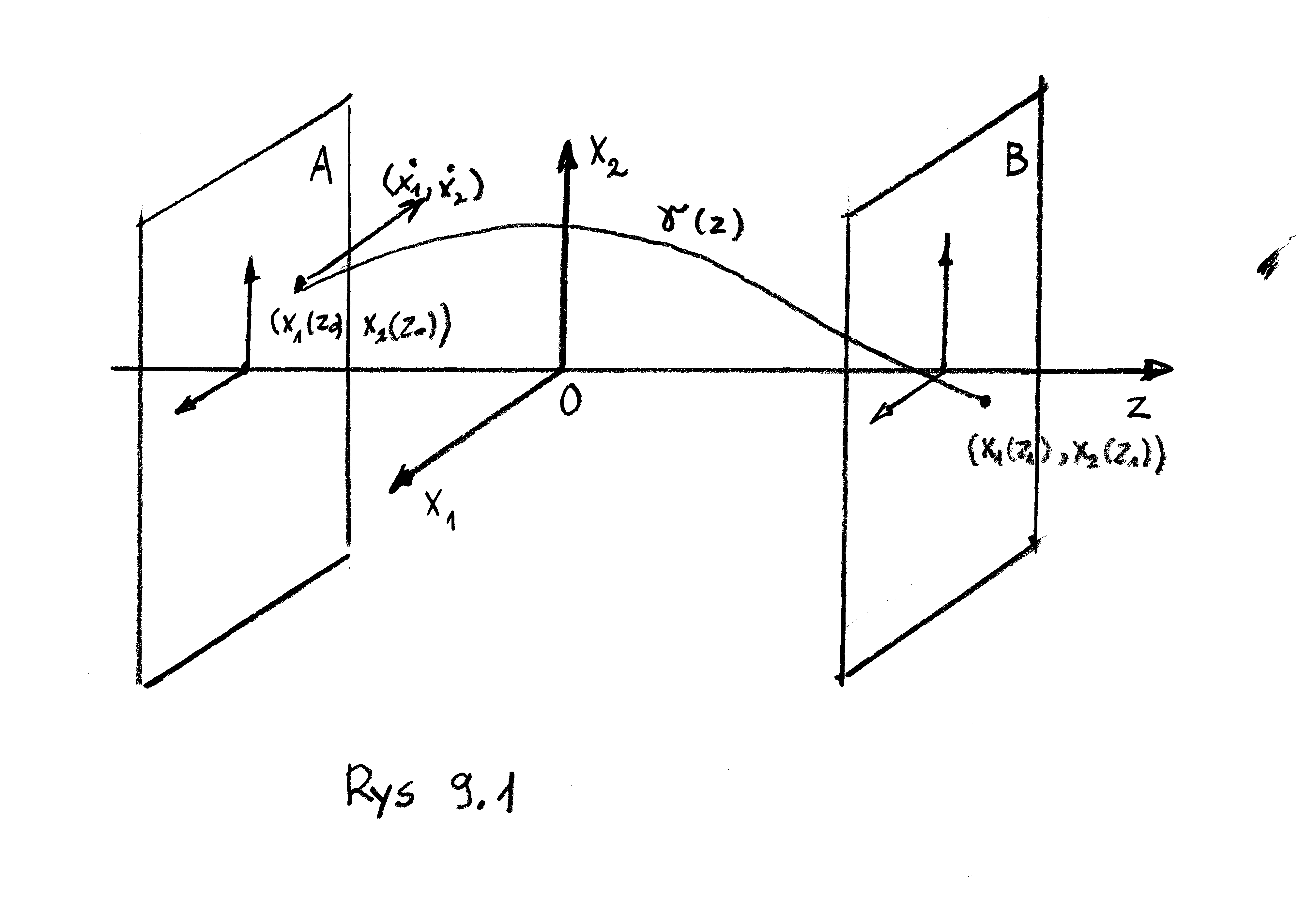
Optyka geometryczna nie wnika w fizyczną naturę światła lecz przyjmuje jako aksjomat, że droga promienia światlnego jest taką krzywą, która minimalizuje tzw. długość optyczną. Ta zasada wariacyjna, której precyzyjne sformułowanie podamy w dalszej części wykładu, ma związek z zasadą Fermata, mówiącą, że światło biegnąc od punktu do punktu wybiera drogę o najkrótszym czasie przejścia. Schemat przyjęty w optyce geometrycznej przedstawia się następująco:
Rozważmy ”oś optyczną” ![]() którą wyobrazimy sobie jako prostą poziomą, leżącą w płaszczyźnie rysunku. Prostopadle do niej umieścimy dwie płaszczyzny A i B. Są one równoległe do dwóch pozostałych osi kartezjańskiego układu prostokątnego: poziomej osi
którą wyobrazimy sobie jako prostą poziomą, leżącą w płaszczyźnie rysunku. Prostopadle do niej umieścimy dwie płaszczyzny A i B. Są one równoległe do dwóch pozostałych osi kartezjańskiego układu prostokątnego: poziomej osi ![]() i pionowej osi
i pionowej osi ![]()
Przestrzeń między tymi płaszczyznami nazwiemy systemem optycznym. Jest ona scharakteryzowana za pomocą funkcji ![]() - ”gęstości optycznej środowiska”, przez które przebiega promień świetlny. Będziemy dalej zakładać, że tory promieni świetlnych są krzywymi rzutującymi się dyfeomorficznie na oś optyczną t.j, że dopuszczają opis
- ”gęstości optycznej środowiska”, przez które przebiega promień świetlny. Będziemy dalej zakładać, że tory promieni świetlnych są krzywymi rzutującymi się dyfeomorficznie na oś optyczną t.j, że dopuszczają opis ![]() Gęstość optyczna kształtuje tor następującą zasadą Fermata:
promień świetlny opuszczający płaszczyznę A w punkcie
Gęstość optyczna kształtuje tor następującą zasadą Fermata:
promień świetlny opuszczający płaszczyznę A w punkcie ![]() i w kierunku wyznaczonym przez
i w kierunku wyznaczonym przez ![]() a następnie docierający do płaszczyzny
a następnie docierający do płaszczyzny ![]() z analogicznymi współrzędnymi
z analogicznymi współrzędnymi ![]() robi to tak, że minimalizuje ”długość optyczną”
robi to tak, że minimalizuje ”długość optyczną”
| (9.5) |
gdzie ![]() oznacza
oznacza ![]() a
a ![]() oznacza
oznacza ![]() Mamy zatem zagadnienie wariacyjne z funkcją Lagrange'a
Mamy zatem zagadnienie wariacyjne z funkcją Lagrange'a
| (9.6) |
Wynik Hamiltona mówi, że po właściwej zmianie współrzędnych krzywe całkowe równań Eulera dla (9.5) są krzywymi całkowym ”gradientu symplektycznego”' funkcji ![]() Omówimy kolejno dokonywaną zamianę współrzędnych, której istotą jest transformata Legendre'a oraz wyprowadzimy równania Hamiltona, odkładając geometryczną interpretację tej sytuacji do następnego wykładu.
Omówimy kolejno dokonywaną zamianę współrzędnych, której istotą jest transformata Legendre'a oraz wyprowadzimy równania Hamiltona, odkładając geometryczną interpretację tej sytuacji do następnego wykładu.
9.3. Legendre'owska zamiana współrzędnych.
Istotnie, otrzymujemy ( dla zwięzłości będziemy pisać ![]() zamiast
zamiast ![]()
zatem druga różniczka ![]() jest formą kwadratową o postaci:
jest formą kwadratową o postaci:
ale dla
mamy
Na mocy Lematu 9.1, ustalając zmienne ![]() możemy stosować Stwierdzenie 9.1 do funkcji:
możemy stosować Stwierdzenie 9.1 do funkcji:
określając odwzorowanie
| (9.7) |
i odwzorowanie odwrotne
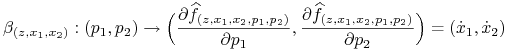 |
(9.8) |
W dalszym ciągu, dla oszczędności miejsca, będziemy zapisywać
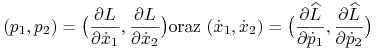 |
9.4. Wyprowadzenie równań Hamiltona
Napiszmy układ równań Eulera dla funkcjonału (9.5)
| (9.9) |
i zastąpmy w nim ![]() przez nową zmienną
przez nową zmienną ![]() (zgodnie z 9.7). Oznaczając
(zgodnie z 9.7). Oznaczając ![]() przez
przez ![]()
![]() możemy zapisać wtedy (9.9) w postaci:
możemy zapisać wtedy (9.9) w postaci:
| (9.10) |
Otrzymujemy w ten sposób pierwsze dwa równania. Ponieważ ![]() zależą od
zależą od ![]() chcąc zastąpić
chcąc zastąpić ![]() przez
przez ![]() możemy skorzystać z odwrotnej transformacji Legendre'a (9.8) dodając do (9.10) warunki
możemy skorzystać z odwrotnej transformacji Legendre'a (9.8) dodając do (9.10) warunki
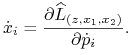 |
(9.11) |
To, że układ warunków (9.10) i (9.11) daje układ czterech równań określających funkcje ![]() i
i ![]() wynika z następującego lematu.
wynika z następującego lematu.
Lemat 9.2
Niech dla ustalonych ![]() funkcja
funkcja ![]() oznacza transformatę Legendre'a funkcji
oznacza transformatę Legendre'a funkcji ![]()
Wtedy
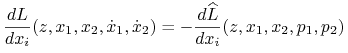 |
(9.12) |
Funkcje ![]() oraz
oraz ![]() związane są warunkiem
związane są warunkiem
| (9.13) |
gdzie ![]() przy ustalonych
przy ustalonych ![]()
Obliczając ![]() dla lewej strony (9.13) otrzymamy
dla lewej strony (9.13) otrzymamy
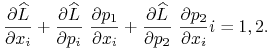 |
Dla prawej strony 9.13 otrzymamy wyrażenie
Ale
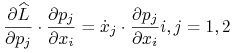 |
skąd wynika (9.12).
∎Na mocy lematu (9.4.) możemy więc przekształcić równanie (9.10), otrzymując ostateczny układ równań Hamiltona
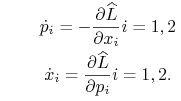 |
(9.14) |
Wobec tego trudność przejścia od opisu wariacyjnego z funkcją Lagrange'a ![]() do opisu (9.14) polega na znalezieniu transformaty Legendre'a
do opisu (9.14) polega na znalezieniu transformaty Legendre'a ![]() funkcji
funkcji ![]() Oczywiście cała procedura opiera się na założeniu, że przy ustalonych
Oczywiście cała procedura opiera się na założeniu, że przy ustalonych ![]() funkcja
funkcja ![]() jest funkcją wypukłą ze względu na zmienne
jest funkcją wypukłą ze względu na zmienne ![]() i
i ![]()
Pokażemy teraz, jak wygląda ![]() dla funkcji Lagrange'a
dla funkcji Lagrange'a
W dalszym ciągu, dla zwięzłości, będziemy pisać ![]() zamiast
zamiast ![]() Wtedy (por. dowód lematu 9.1)
Wtedy (por. dowód lematu 9.1)
skąd
Zauważmy, że zachodzi tożsamość
a więc
i ostatecznie
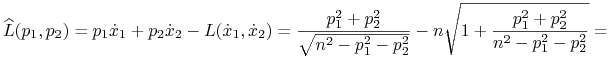 |
Podsumowując: