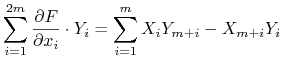Zagadnienia
10. Mechanika Hamiltonowska
10.1. Równania Hamiltona
Twierdzenie 10.1
Niech ![]() będzie układem mechanicznym z funkcją Lagrange'a
będzie układem mechanicznym z funkcją Lagrange'a ![]() gdzie energia kinetyczna ma postać formy kwadratowej zmiennych
gdzie energia kinetyczna ma postać formy kwadratowej zmiennych ![]() to jest
to jest
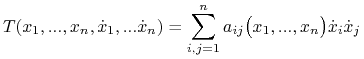 |
(10.1) |
Załóżmy, że dla dowolnych ustalonych ![]() forma (10.1) jest dodatnio określona.
Wtedy
(a) po dokonaniu zamiany zmiennych
forma (10.1) jest dodatnio określona.
Wtedy
(a) po dokonaniu zamiany zmiennych
| (10.2) |
analogicznie, jak w (9.7), gdzie przekształcenie odwrotne dane jest wzorem
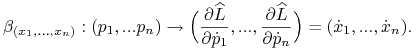 |
(10.3) |
Układ równań Eulera - Lagrange'a
| (10.4) |
przechodzi na układ Hamiltona
![\left\{\begin{array}[]{ll}\dot{p}_{i}=-\frac{\partial\widehat{L}}{\partial{x}_{i}}\\
&\textrm{i=1, 2,..,n}\\
\dot{x}_{i}=-\frac{\partial\widehat{L}}{\partial{p}_{i}}\end{array}\right.](wyklady/mmk/mi/mi1191.png) |
(10.5) |
(b) Wartość transformaty Lagrange'a ![]() jest równa energii całkowitej układu
jest równa energii całkowitej układu ![]() w punkcie
w punkcie
![]() , gdzie
, gdzie ![]()
(a) Wyprowadzenie równań (10.5) przebiega analogicznie, jak w przypadku równań (9.14) w poprzednim wykładzie i nie będziemy tego rozumowania powtarzać.
(b) Dla zwięzłości wzorów napiszemy ![]() zamiast
zamiast ![]()
![]() zamiast
zamiast ![]() i
i ![]() zamiast
zamiast ![]() Twierdzimy, że zachodzi równość
Twierdzimy, że zachodzi równość
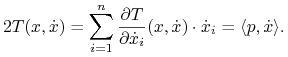 |
Istotnie, rozpatrując macierz formy (10.1) widzimy, że zmienna ![]() występuje tylko w i-tym wierszu i w i-tej kolumnie. Wobec tego
występuje tylko w i-tym wierszu i w i-tej kolumnie. Wobec tego
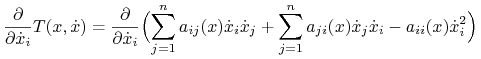 |
zatem
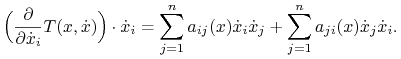 |
Wobec tego tworząc sumę 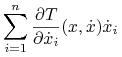 uzyskamy w niej każdy wyraz
uzyskamy w niej każdy wyraz
![]() dwukrotnie - raz jako stojący w i-tym wierszu a raz jako stojący w j-tej kolumnie.
Zatem
dwukrotnie - raz jako stojący w i-tym wierszu a raz jako stojący w j-tej kolumnie.
Zatem
| (10.6) |
Definicja 10.1
Transformatę Legendre'a funkcji Lagrange'a układu mechanicznego nazywamy funkcją Hamiltona lub hamiltonianem tego układu i oznaczamy literą H.
Ćwiczenie 10.1
Podać hamiltonian układu n-punktów z potencjałem ![]() i bez więzów. Napisać równania Hamiltona.
i bez więzów. Napisać równania Hamiltona.
Oznaczmy położenie ![]() tego punktu o masie
tego punktu o masie ![]() przez
przez ![]() Zgodnie z Definicją(10.1) i formułą (10.6) mamy
Zgodnie z Definicją(10.1) i formułą (10.6) mamy
gdzie
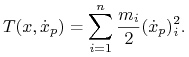 |
Na podstawie ćwiczenia (9.1) otrzymamy 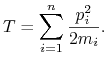
Hamiltonian układu ma więc postać
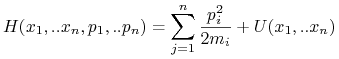 |
a równania Hamiltona wyglądają następująco
10.2. Informacje o geometrii symplektycznej.
W ustępie tym, inaczej niż w całym wykładzie, założymy znajomość kilku podstawowych pojęć geometrii różniczkowej. I tak dla sformułowania potrzebnych definicji potrzebować będziemy pojęć wiązki stycznej i wiązki kostycznej do rozmaitości różniczkowej a także założymy, że czytelnik ma podstawowe doświadczenie w operowaniu formami różniczkowymi. Sytuacja ta nie jest kontynuowana w dalszym ciągu wykładu i bez szkody dla jego zrozumienia można pominąć szczegóły techniczne.
Zacznijmy od algebry liniowej. Niech ![]() będzie bazą
będzie bazą ![]() i niech
i niech
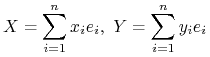 |
oraz niech
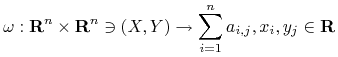 |
(10.7) |
Formę (10.7) można zapisać w postaci macierzowej
| (10.8) |
gdzie ![]() jest macierzą o jednej kolumnie, składającej się ze współrzędnych wektora
jest macierzą o jednej kolumnie, składającej się ze współrzędnych wektora ![]() względem bazy
względem bazy ![]() ,
, ![]() jest macierzą o jednym wierszu, składającym się się ze współrzędnych
jest macierzą o jednym wierszu, składającym się się ze współrzędnych ![]() względem tejże bazy. Natomiast
względem tejże bazy. Natomiast ![]() jest macierzą współczynników (występujących w (10.7)) wymiaru
jest macierzą współczynników (występujących w (10.7)) wymiaru ![]() Wtedy wynik mnożenia w (10.8) jest macierzą
Wtedy wynik mnożenia w (10.8) jest macierzą ![]() której jedyny współczynnik jest liczbą występującą na prawo od strzałki we wzorze (10.7).
Powiemy, że forma jest nieosobliwa, jeżeli zachodzi implikacja:
której jedyny współczynnik jest liczbą występującą na prawo od strzałki we wzorze (10.7).
Powiemy, że forma jest nieosobliwa, jeżeli zachodzi implikacja:
Powiemy, że forma jest antysymetryczna, jeżeli ![]() Następujące dwie własności opisu macierzowego (10.8) występują w podstawowym kursie algebry liniowej i ich dowody pominiemy.
Następujące dwie własności opisu macierzowego (10.8) występują w podstawowym kursie algebry liniowej i ich dowody pominiemy.
Stwierdzenie 10.1
(a) ( ![]() jest antysymetryczna )
jest antysymetryczna ) ![]()
(b) ( ![]() jest nieosobliwa)
jest nieosobliwa) ![]() ( det
( det ![]()
Stwierdzenie 10.2
Niech ![]() będzie antysymetryczną i nieosobliwą formą dwuliniową. Wtedy
będzie antysymetryczną i nieosobliwą formą dwuliniową. Wtedy
(a) ![]()
(b) Istnieje baza ![]() względem której macierz formy
względem której macierz formy ![]() ma postać blokową:
ma postać blokową:
| (10.9) |
gdzie ![]() jest jednostkową macierzą wymiaru
jest jednostkową macierzą wymiaru ![]() .
.
(c) Niech ![]() będzie bazą przestrzeni
będzie bazą przestrzeni ![]() dualną do bazy
dualną do bazy ![]() z punktu (b) wtedy
z punktu (b) wtedy
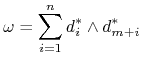 |
(10.10) |
(a) Na mocy Stwierdzenia (10.1) ![]() zatem
zatem ![]() a ponieważ
a ponieważ ![]() otrzymujemy stąd
otrzymujemy stąd ![]()
(b) Indukcja względem ![]() Dla
Dla ![]() rozważmy formę antysymetryczną i nieosobliwą
rozważmy formę antysymetryczną i nieosobliwą ![]() w
w ![]() Z nieosobliwości
Z nieosobliwości ![]() wynika, że istnieją niezerowe wektory
wynika, że istnieją niezerowe wektory ![]() takie, że
takie, że ![]() Wtedy
Wtedy ![]() i
i ![]() są liniowo niezależne.
są liniowo niezależne.
Niech ![]() Macierz
Macierz ![]() formy
formy ![]() względem bazy
względem bazy ![]() ma postać
ma postać
Krok indukcyjny.
Podobnie jak przy ![]() znajdziemy dwa wektory liniowo niezależne
znajdziemy dwa wektory liniowo niezależne ![]() takie, że
takie, że ![]() Niech
Niech
Z liniowej niezależności ![]() i
i ![]() i nieosobliwości
i nieosobliwości ![]() wynika, że
wynika, że ![]() Ponieważ, jak widać ograniczenie
Ponieważ, jak widać ograniczenie ![]() do
do ![]() jest formą nieosobliwą, z założenia indukcyjnego istnieje baza
jest formą nieosobliwą, z założenia indukcyjnego istnieje baza ![]() przestrzeni
przestrzeni ![]() taka, że
taka, że ![]() ograniczona do
ograniczona do ![]() ma względem tej bazy postać (10.9) z indeksem
ma względem tej bazy postać (10.9) z indeksem ![]() . Wtedy baza
. Wtedy baza ![]() spełnia tezę Stwierdzenia.
spełnia tezę Stwierdzenia.
(c) Niech ![]() będzie bazą
będzie bazą ![]() dualną do bazy
dualną do bazy ![]() skonstruowanej w punkcie (b). Wtedy macierz 2-formy
skonstruowanej w punkcie (b). Wtedy macierz 2-formy ![]() ma postać
ma postać
gdzie ![]() jest macierzą
jest macierzą ![]() mającą same zera z wyjątkiem i-tego miejsca na przekątnej, gdzie występuje jedynka. Stąd i z formuły (10.9) wynika przedstawienie (10.9).
mającą same zera z wyjątkiem i-tego miejsca na przekątnej, gdzie występuje jedynka. Stąd i z formuły (10.9) wynika przedstawienie (10.9).
Ze Stwierdzenia (10.2) wynika, że w ![]() wymiarowej przestrzeni rzeczywistej wszystkie nieosobliwe i antysymetryczne formy dwuliniowe są do siebie podobne w tym sensie, że opisywane są tą samą macierzą
wymiarowej przestrzeni rzeczywistej wszystkie nieosobliwe i antysymetryczne formy dwuliniowe są do siebie podobne w tym sensie, że opisywane są tą samą macierzą ![]() tyle, że względem różnych baz.
tyle, że względem różnych baz.
Definicja 10.2
Tę jedyną (w powyższym sensie) formę na przestrzeni ![]() nazwiemy m-tą formą symplektyczną.
nazwiemy m-tą formą symplektyczną.
Definicja 10.3
Rozmaitość różniczkową ![]() wymiaru
wymiaru ![]() nazwiemy rozmaitością symplektyczną jeżeli:
nazwiemy rozmaitością symplektyczną jeżeli:
(a) w każdej przestrzeni stycznej ![]() dla
dla ![]() jest określona forma symplektyczna
jest określona forma symplektyczna ![]() której współczynniki gładko zależą od
której współczynniki gładko zależą od ![]()
(b) tak określona dwuforma różniczkowa ![]() jest zamknięta, tj.
jest zamknięta, tj. ![]()
Poniższe twierdzenie jest lokalnym analogiem ”punktowego” Stwierdzenia (10.2)
Stwierdzenie 10.3
(Darboux)
Niech ![]() będzie 2m-wymiarową rozmaitością symplektyczną z formą
będzie 2m-wymiarową rozmaitością symplektyczną z formą ![]() Dla każdego
Dla każdego ![]() istnieje mapa
istnieje mapa ![]() w otoczeniu
w otoczeniu ![]() taka, że dla
taka, że dla ![]() forma
forma ![]() w każdej przestrzeni
w każdej przestrzeni ![]() ma względem bazy
ma względem bazy ![]() wyznaczonej przez mapę
wyznaczonej przez mapę ![]() macierz (10.9).
macierz (10.9).
Niech będzie dana mapa ![]() Obrazy stałych pól bazowych
Obrazy stałych pól bazowych![]() w
w ![]() za pomocą
za pomocą ![]() zapiszemy jako
zapiszemy jako
Pola te będziemy nazywać polami bazowymi dla mapy ![]() Pola te są przemienne (tj.
Pola te są przemienne (tj.![]() dla i,j, = 1, 2, ..,2n) oraz ich wartości
dla i,j, = 1, 2, ..,2n) oraz ich wartości
![]() stanowią dla każdego
stanowią dla każdego ![]() bazę przestrzeni stycznej
bazę przestrzeni stycznej ![]() Formę
Formę ![]() ograniczoną do
ograniczoną do ![]() oznaczymy
oznaczymy ![]()
Dowód będzie przebiegał za pomocą indukcji względem ![]() gdzie
gdzie ![]()
(a) Niech ![]() niech
niech ![]() oraz niech
oraz niech ![]() będzie mapą w otoczeniu
będzie mapą w otoczeniu ![]() Bez utraty ogólności możemy przyjąć, że
Bez utraty ogólności możemy przyjąć, że ![]() oraz , że
macierz formy
oraz , że
macierz formy ![]() względem bazy
względem bazy ![]() jest równa
jest równa ![]() (
(![]() jak w (10.9)). Znaczy to, że
jak w (10.9)). Znaczy to, że
Zatem dla ![]() bliskich
bliskich ![]() (aby nie komplikować notacji
przyjmijmy, że dla
(aby nie komplikować notacji
przyjmijmy, że dla ![]() ) zachodzi
) zachodzi
Wprowadźmy pola ![]() i
i ![]() zadane formułą:
zadane formułą:
| (10.11) |
Wtedy ![]() ma z bazie
ma z bazie ![]() macierz
macierz ![]() Zauważmy też, że pola
Zauważmy też, że pola ![]() powstają jako pola bazowe dla mapy
powstają jako pola bazowe dla mapy ![]() gdzie dla
gdzie dla ![]() określamy
określamy
(b) Krok indukcyjny.
Niech ![]() i niech
i niech ![]() Postępując, jak w punkcie (a) możemy znaleść mapę
Postępując, jak w punkcie (a) możemy znaleść mapę ![]() w otoczeniu
w otoczeniu ![]() taką, że
taką, że
Określmy na ![]() dwie dystrybucje:
dwie dystrybucje: ![]() i
i ![]() kładąc
kładąc
Lemat 10.1
Dystrybucje ![]() i
i ![]() są różniczkowalne i inwolutywne.
są różniczkowalne i inwolutywne.
Pola ![]() i
i ![]() są różniczkowalne i przemienne, skąd wynika teza dla
są różniczkowalne i przemienne, skąd wynika teza dla ![]() Dla dowodu, że
Dla dowodu, że ![]() jest różniczkowalna, rozważmy pola
jest różniczkowalna, rozważmy pola
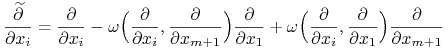 |
(10.12) |
Są one różniczkowalne, liniowo niezależne w każdym punkcie i dla ![]() należą do
należą do ![]() Zatem dystrybucja
Zatem dystrybucja ![]() jest różniczkowalna.
Dla inwolutywności
jest różniczkowalna.
Dla inwolutywności ![]() zauważmy, że warunek
zauważmy, że warunek ![]() można zapisać w formie dwóch warunków:
można zapisać w formie dwóch warunków:
| (10.13) |
gdzie ![]() jest formą liniową
jest formą liniową ![]() Tak więc, aby pokazać, że dla
Tak więc, aby pokazać, że dla ![]() jak i
jak i ![]() także
także ![]() wystarczy udowodnić, że
wystarczy udowodnić, że
Dla dowodu tych warunków posłużymy się następującymi własnościami pochodnej Liego (por. Stwierdzenie (11.1)).
| (10.14) |
gdzie ![]() jest dowolną dwuformą, oraz
jest dowolną dwuformą, oraz
| (10.15) |
Zwężając obie strony równości (10.14) przy ![]() kolejno z polem
kolejno z polem ![]() oraz
oraz ![]() otrzymamy dla
otrzymamy dla ![]()
i stosując do wyrażeń po prawej stronie ostatniej równości własność (10.15) dostaniemy
bo wnętrza nawiasów są równe 0 na mocy założenia (10.13).
Na mocy Lematu i Twierdzenia Frobeniusa obie dystrybucje ![]() i
i ![]() są całkowalne, tj przez każdy punkt
są całkowalne, tj przez każdy punkt ![]() rozmaitości
rozmaitości ![]() przechodzą dwie podrozmaitości
przechodzą dwie podrozmaitości ![]() i
i ![]() takie, że
takie, że ![]() i
i ![]() można utożsamić z przestrzenią
można utożsamić z przestrzenią ![]() i
i ![]() odpowiednio.
Forma
odpowiednio.
Forma ![]() ograniczona do
ograniczona do ![]() i do
i do ![]() pozostaje domknięta i nieosobliwa. Zatem, z założenia indukcyjnego, istnieje mapa w otoczeniu
pozostaje domknięta i nieosobliwa. Zatem, z założenia indukcyjnego, istnieje mapa w otoczeniu ![]() w
w ![]() dla której zachodzi teza Stwierdzenia (10.3). Produkt tej mapy i mapy w
dla której zachodzi teza Stwierdzenia (10.3). Produkt tej mapy i mapy w ![]() daje żądaną mapę na
daje żądaną mapę na ![]()
Wniosek 10.1
Stwierdzenie (10.3) mówi, że każde dwie rozmaitości symplektyczne ustalonego wymiaru ![]() są lokalnie identyczne z otoczeniem zera w
są lokalnie identyczne z otoczeniem zera w ![]() wyposażonym w formę:
wyposażonym w formę:
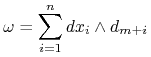 |
(10.16) |
Każdą mapę na ![]() której forma
której forma ![]() ma postać (10.16) nazywamy mapą kanoniczną.
ma postać (10.16) nazywamy mapą kanoniczną.
Definicja 10.4
Niech ![]() będzie funkcją różniczkowalną na rozmaitości symplektycznej
będzie funkcją różniczkowalną na rozmaitości symplektycznej ![]() Gradientem symplektycznym funkcji
Gradientem symplektycznym funkcji ![]() (lub polem hamiltonowskim wyznaczonym przez
(lub polem hamiltonowskim wyznaczonym przez ![]() ) nazwiemy (jedyne) pole wektorowe
) nazwiemy (jedyne) pole wektorowe ![]() na
na ![]() spełaniające warunek:
spełaniające warunek:
dla każdego różniczkowalnego pola ![]() na
na ![]()
| (10.17) |
Gradient symplektyczny ![]() związany z formą
związany z formą ![]() oznaczymy
oznaczymy ![]()
Uwaga 10.1
Podobnie, jak w (10.9) ale używając macierzy jednostkowej zamiast macierzy (10.9) definiujemy ”zwykły ” gradient w ![]()
Ćwiczenie 10.2
Wyznaczyć postać gradientu symplektycznego funkcji ![]() w mapie kanonicznej.
w mapie kanonicznej.
10.3. Kanoniczna struktura symplektyczna na wiązce kostycznej do rozmaitości.
Niech ![]() będzie rozmaitością różniczkową wymiaru
będzie rozmaitością różniczkową wymiaru ![]() Oznaczmy przez
Oznaczmy przez ![]() wiązkę styczną a przez
wiązkę styczną a przez ![]() wiązkę kostyczną do
wiązkę kostyczną do ![]() Niech
Niech ![]() będzie kanoniczną projekcją (tj. odwzorowaniem przeprowadzającym wszystkie elementy przestrzeni kostycznej do
będzie kanoniczną projekcją (tj. odwzorowaniem przeprowadzającym wszystkie elementy przestrzeni kostycznej do ![]() w dowolnym ustalonym
w dowolnym ustalonym ![]() na
na ![]() Niech
Niech ![]() będzie przekształceniem indukowanym przez
będzie przekształceniem indukowanym przez ![]() (podniesieniem
(podniesieniem ![]() do wiązki stycznej, różniczką
do wiązki stycznej, różniczką ![]() ).
Dla ustalonej mapy
).
Dla ustalonej mapy ![]() na
na ![]() oraz
oraz ![]() niech
niech ![]() będzie bazą w
będzie bazą w ![]() (Zobacz dowód Stwierdzenia (10.3)). I niech
(Zobacz dowód Stwierdzenia (10.3)). I niech ![]() będzie dualną bazą przestrzeni
będzie dualną bazą przestrzeni ![]() Jednoformy
Jednoformy ![]() pozwalają utożsamiać
pozwalają utożsamiać ![]() z produktem
z produktem ![]() za pomocą odwzorowania
za pomocą odwzorowania ![]() danego wzorem:
danego wzorem:
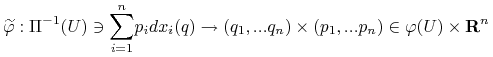 |
(10.20) |
gdzie ![]() dla
dla ![]() Parę
Parę ![]() nazwiemy mapą na
nazwiemy mapą na ![]() indukowaną przez mapę
indukowaną przez mapę ![]() na
na ![]() Punkty
Punkty ![]() będziemy oznaczać za pomocą ich współrzędnych
będziemy oznaczać za pomocą ich współrzędnych ![]() w mapie indukowanej. Niech
w mapie indukowanej. Niech ![]() będzie polem wektorowym na
będzie polem wektorowym na ![]() Wtedy
Wtedy ![]() w punkcie
w punkcie ![]() ma postać
ma postać
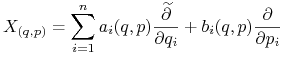 |
(10.21) |
gdzie
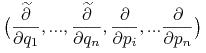 |
sa polami bazowymi na ![]() związanymi z mapą
związanymi z mapą ![]() Przy czym
Przy czym ![]() oznacza teraz pole na
oznacza teraz pole na ![]() które przy lokalnym ”ilorazowym” przedstawieniu
które przy lokalnym ”ilorazowym” przedstawieniu ![]() w formie (10.20) odpowiada polu
w formie (10.20) odpowiada polu ![]() na
na ![]() Widzimy, że wtedy
Widzimy, że wtedy
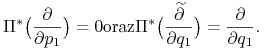 |
A więc
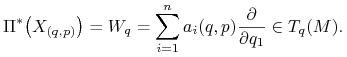 |
Na to pole wektorowe podziałajmy formą ![]() na
na ![]() której wartość w
której wartość w ![]() ma postać
ma postać
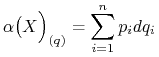 |
i zależy tylko od współrzędnych ![]() Otrzymamy więc przyporządkowanie
Otrzymamy więc przyporządkowanie
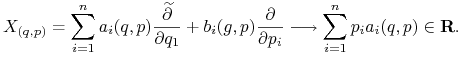 |
To przyporządkowanie jest dla każdego ustalonego ![]() liniową operacją na
liniową operacją na ![]() a więc wyznacza formę liniową na
a więc wyznacza formę liniową na ![]() Ta forma mnoży współrzędne przy
Ta forma mnoży współrzędne przy ![]() przez liczbę
przez liczbę ![]() Zatem postać jednoformy, którą w ten sposób uzyskujemy jest
Zatem postać jednoformy, którą w ten sposób uzyskujemy jest
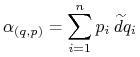 |
(10.22) |
gdzie ![]() oznacza formę na
oznacza formę na ![]() która przy ”ilorazowym” przedstawieniu
która przy ”ilorazowym” przedstawieniu ![]() w formie (10.20)odpowiada formie
w formie (10.20)odpowiada formie ![]() na
na ![]() Formę (10.22) nazywa się formą Liouville'a n
Formę (10.22) nazywa się formą Liouville'a n ![]()
Niech ![]() Wtedy
Wtedy ![]() jest zamkniętą dwuformą o postaci:
jest zamkniętą dwuformą o postaci:
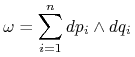 |
(10.23) |
Zatem jest nieosobliwą w każdym punkcie (por. Stwierdzenie(10.2) (c)).
Zgodnie z przyjętą powszechnie konwencją, piszemy tu ![]() zamiast bardziej poprawnego formalnie
zamiast bardziej poprawnego formalnie ![]()
Stwierdzenie 10.4
Na wiązce kostycznej ![]() do dowolnej rozmaitości różniczkowej
do dowolnej rozmaitości różniczkowej ![]() istnieje forma symplektyczna
istnieje forma symplektyczna ![]() która w mapach indukowanych przez mapy na
która w mapach indukowanych przez mapy na ![]() ma postać kanoniczną (10.22). Własność ta wyznacza formę
ma postać kanoniczną (10.22). Własność ta wyznacza formę ![]()