Zagadnienia
2. Różne rodzaje sił
Siły, jakie obserwujemy, są kilku rodzajów. Po pierwsze są to siły pochodzące od istot żywych. Ich natura jest skomplikowana i nie będziemy się nimi tutaj zajmować. Drugim rodzajem sił są siły związane z urządzeniami mechanicznymi. Studiowanie ich oraz ich skutków w postaci ruchu mechanizmów jest w oczywisty sposób związane z projektowaniem tych ostatnich. Proste realizacje takich sytuacji występują w Przykładach 1.4 i 1.6 z poprzedniego wykładu. Trzecim rodzajem sił są ”siły przyrody”. Okazuje się, że są one czterech rodzajów, z których dwa: siły grawitacyjne i siły elektromagnetyczne występują w skali makro, natomiast dwa inne rodzaje - tzw. oddziaływania mocne i słabe są właściwie dla świata mikro. Teoria oddziaływań mocnych i słabych należy do zaawansowanych fragmentów fizyki teoretycznej i jest poza obszarem naszych obecnych zainteresowań. Pozostają nam więc oddziaływania grawitacyjne i elektomagnetyczne. Teoria tych ostatnich dotyczy w znacznej mierze obiektów poruszających się z wielkimi prędkościami, gdzie jedno z naszych wstępnych założeń o bezwzględności czasu musi zostać zakwestionowane. Sytuacja ta tłumaczy widoczną w przytoczonych przykładach jednorodność rodzaju występujących sił. Większość z nich to (ewentualnie) przetransformowane, jak w Przykładzie 1.5 siły grawitacyjne.
2.1. Siły zachowawcze
W dyskutowanych poprzednio przykładach wszystkie siły (poza Przykładem 1.2) zależały tylko od położenia i nie zależały od czasu. Niezależność od czasu prawych stron dyskutowanych równań ma liczne implikacje matematyczne. Oto jedna z nich:
Uwaga 2.1
Jeżeli siła ![]() w (1.4) nie zależy od czasu ani od prędkości
w (1.4) nie zależy od czasu ani od prędkości ![]() to wraz z
to wraz z ![]() funkcja
funkcja ![]() jest rozwiązaniem (1.4).
Istotnie, dla
jest rozwiązaniem (1.4).
Istotnie, dla ![]() widzimy, że
widzimy, że ![]() oraz
oraz ![]() . Zatem
. Zatem
Wynika stąd, że (pomijając mało istotny wpływ pozostałych planet) wraz z ruchem planety po orbicie wokół Słońca, możliwy jest ruch po tej samej orbicie w odwrotnym kierunku, który możemy otrzymać niejako odwracając bieg czasu. Ten ”odwrócony” porządek możemy zrealizować w normalnym świecie, zmieniając np.
warunki początkowe w chwili 0 z ![]() na
na ![]()
2.2. Siły potencjalne.
W elementarnym kursie fizyki definiuje się pracę ![]() stałej siły
stałej siły ![]() na prostoliniowej drodze
na prostoliniowej drodze ![]() przy założeniu, że siła jest
równoległa do tej drogi i zgodnie z nią skierowana wzorem:
przy założeniu, że siła jest
równoległa do tej drogi i zgodnie z nią skierowana wzorem:
| (2.1) |
gdzie ![]() oznacza długość drogi.
Zatem pracę stałego pola
oznacza długość drogi.
Zatem pracę stałego pola ![]() określonego na odcinku
określonego na odcinku ![]() prostej zanurzonej w
prostej zanurzonej w ![]() możemy przyjąć jako
możemy przyjąć jako
| (2.2) |
gdzie ![]() jest iloczynem skalarnym w
jest iloczynem skalarnym w ![]() ,
, ![]() jest długością odcinka
jest długością odcinka ![]() , natomiast
, natomiast ![]() jest długością rzutu wektora
jest długością rzutu wektora ![]() na oś wyznaczoną przez
na oś wyznaczoną przez ![]() .
.
Wzór (2.2) jest krokiem wstępnym do określenia pracy ![]() gładkiego pola wektorowego
gładkiego pola wektorowego ![]() , wzdłuż gładkiej krzywej
, wzdłuż gładkiej krzywej ![]() .
Przypomnimy znany z kursu Analizy II sens tego symbolu.
.
Przypomnimy znany z kursu Analizy II sens tego symbolu.
Niech ![]() będzie krzywą klasy
będzie krzywą klasy ![]() , (tj. krzywą mającą ciągłą pochodną na
, (tj. krzywą mającą ciągłą pochodną na ![]() ). Dla skończonego podziału
). Dla skończonego podziału
| (2.3) |
odcinka ![]() utwórzmy sumę całkową:
utwórzmy sumę całkową:
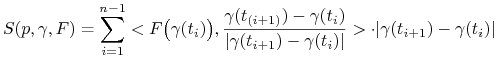 |
(2.4) |
której każdy składnik jest postaci (2.2). Następnie dla normalnego ciągu podziałów ![]() rozpatrzmy granicę:
rozpatrzmy granicę:
| (2.5) |
(Ciąg podziałów ![]() nazywamy normalnym, jeżeli największa z różnic
nazywamy normalnym, jeżeli największa z różnic ![]() między kolejnymi punktami tworzącymi k-ty podział, dąży do zera przy
między kolejnymi punktami tworzącymi k-ty podział, dąży do zera przy ![]() .)
.)
Korzystając z różniczkowalności ![]() oraz
oraz ![]() , pokazuje się, że dla dostatecznie drobnego podziału
, pokazuje się, że dla dostatecznie drobnego podziału ![]() różnica
różnica
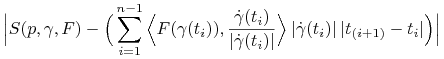 |
(2.6) |
może być tak mała, jak chcemy.
Część druga (odjemnik) powyższej różnicy jest sumą całkową dla funkcji ![]() .
Wynika stąd, że sumy (2.4) mają dla każdego normalnego ciągu podziału granicę równą
.
Wynika stąd, że sumy (2.4) mają dla każdego normalnego ciągu podziału granicę równą
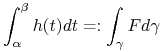 |
(2.7) |
Tak wprowadzona całka mogłaby zależeć od parametryzacji krzywej ![]() . Dowodzi się, że tak jednak nie jest.W dalszym ciągu wykorzystamy dwie następujące jej własności, które przyjmiemy bez dowodu:
. Dowodzi się, że tak jednak nie jest.W dalszym ciągu wykorzystamy dwie następujące jej własności, które przyjmiemy bez dowodu:
Stwierdzenie 2.1
Jeżeli ![]() jest kawałkami gładką krzywą, będącą sumą dwóch rozłącznych części
jest kawałkami gładką krzywą, będącą sumą dwóch rozłącznych części ![]() i
i ![]() , wtedy dla dowolnego kawałkami gładkiego pola wektorowego
, wtedy dla dowolnego kawałkami gładkiego pola wektorowego ![]() zachodzi:
zachodzi:
| (2.8) |
Jeżeli ![]() oznacza krzywą
oznacza krzywą ![]() przebieganą w przeciwnym kierunku to
przebieganą w przeciwnym kierunku to
| (2.9) |
Odpowiedź na poniższe pytanie ma podstawowe znaczenie dla tego wykładu.
Problem 2.1
Dane jest gładkie pole wektorowe ![]() określone na
określone na ![]() . Kiedy dla każdej pary krzywych
. Kiedy dla każdej pary krzywych ![]() i
i ![]() leżących w
leżących w ![]() i łączących te same punkty zachodzi równość
i łączących te same punkty zachodzi równość
| (2.10) |
O sytuacji opisanej wzorem (2.10) powiemy krótko, że praca pola nie zależy od drogi całkowania. Zanim ustosunkujemy się do Problemu 2.1, rozpatrzmy proste zadanie:
Ćwiczenie 2.1
Na zboczu rozległej góry znajdują się dwa domy (zob. rysunek poniżej). Łączą je dwie drogi. Pokazać, że (nie uwzględniając sił tarcia) człowiek ciągnący wózek z ładunkiem z domu A do domu B po każdej z tych dróg wykonuje taką samą pracę, której wielkość zależy tylko od różnicy wysokości położenia domów.
Zacznijmy od uściślenia sformułowań. Posuwając się pod górę pokonujemy opór siły z jaką Ziemia przyciąga wózek a dokładniej opór rzutu tej siły na oś styczną do drogi w jej aktualnym miejscu. Chcemy robić to możliwie ekonomicznie, nie rozpędzając niepotrzebnie wózka (porównaj początek następnego wykładu). W rezultacie, (co jest teoretyczną idealizacją), będziemy zakładać, że siła, którą działamy jest przeciwna do wyżej wymienionego rzutu siły ciężkości. Analogiczne założenie należy przyjąć w tej części drogi, kiedy posuwamy się w dół. Wprowadźmy układ współrzędnych prostokątnych, którego trzecia oś jest skierowana pionowo do góry. Siła, która popycha wózek, kiedy jedzie z góry lub którą trzeba przezwyciężyć, ciągnąc go pod górę, jest składową styczną do drogi siły (0,0 -![]() ). Porównaj Przykład (1.2), gdzie
). Porównaj Przykład (1.2), gdzie ![]() jest masą grawitacyjną wózka a
jest masą grawitacyjną wózka a ![]() przyspieszeniem ziemskim. Rozpatrzmy i-ty wyraz sumy całkowej (2.4), który (po uproszczeniu) jest równy:
przyspieszeniem ziemskim. Rozpatrzmy i-ty wyraz sumy całkowej (2.4), który (po uproszczeniu) jest równy:
gdzie ![]() jest różnicą poziomów punktów
jest różnicą poziomów punktów ![]() i
i ![]() . Zatem całka od
. Zatem całka od ![]() do
do ![]() po każdej z tych dróg jest równa
po każdej z tych dróg jest równa ![]() gdzie
gdzie ![]() jest różnicą poziomów domów
jest różnicą poziomów domów ![]() i
i ![]() .
.
Możemy teraz podać odpowiedź na postawione pytanie:
Twierdzenie 2.1
Dane jest gładkie pole wektorowe ![]() , określone na otwartym podzbiorze
, określone na otwartym podzbiorze ![]() Następujące warunki są równoważne:
Następujące warunki są równoważne:
-
Praca pola
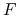 jest niezależna od drogi całkowania w
jest niezależna od drogi całkowania w 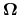 .
. -
Praca pola
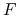 wzdłuż dowolnej krzywej zamkniętej w
wzdłuż dowolnej krzywej zamkniętej w 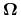 wynosi 0.
wynosi 0. -
Istnieje funkcja gładka
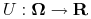 taka, że:
taka, że: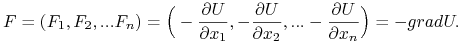
(2.11)
.
Uwaga 2.2
Z matematycznego punktu widzenia można oczywiście zamiast poprzedniej formuły, zmieniając ![]() na
na ![]() , napisać warunek:
, napisać warunek:
| (2.12) |
Ponieważ (jak w naszym przykładzie), chcemy aby ruch wywołany siłą pochodzącą od potencjału odbywał się w kierunku jego mniejszych wartości, przyjmiemy znak '-' przed gradientem.
(Szkic)
Równoważność ![]() jest oczywista. Naszkicujemy dowody implikacji
jest oczywista. Naszkicujemy dowody implikacji ![]() oraz
oraz ![]() .
.
Dowód implikacji ![]() .
Ponieważ wszystkie prace danej siły F po możliwych gładkich krzywych łączących dwa ustalone punkty
.
Ponieważ wszystkie prace danej siły F po możliwych gładkich krzywych łączących dwa ustalone punkty ![]() są z założenia równe, będziemy oznaczać je
są z założenia równe, będziemy oznaczać je ![]() . Wybierzmy punkt
. Wybierzmy punkt ![]() i niech
i niech
Chcemy pokazać, że dla każdego ![]() i
i ![]() zachodzi:
zachodzi:
Niech ![]() będzie wersorem i-tej osi i napiszmy iloraz różnicowy:
będzie wersorem i-tej osi i napiszmy iloraz różnicowy:
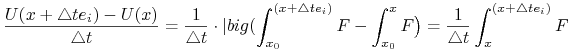 |
Obierając drogę łączącą ![]() z
z ![]() w postaci
w postaci ![]() otrzymamy
otrzymamy ![]() , a zatem zgodnie z (2.7)
, a zatem zgodnie z (2.7)
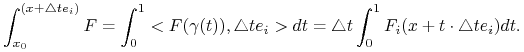 |
W rezultacie, korzystając z twierdzenia o wartości średniej dla całek, otrzymamy (gdzie ![]()
Dowód implikacji ![]()
Niech ![]() będzie ustaloną krzywą łączącą
będzie ustaloną krzywą łączącą ![]() z
z ![]() . Korzystając z (2.7) otrzymamy:
. Korzystając z (2.7) otrzymamy:
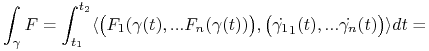 |
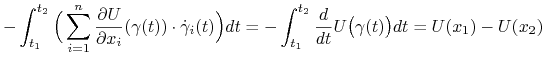 |
(Podobnie, jak w zadaniu 2.3)
∎Przykład 2.1
Wskażemy (bez sprawdzania) potencjały odpowiadające siłom dyskutowanym w przykładach 1.1 - 1.6 z poprzedniego wykładu. Wyniki ujmiemy w następującym zestawieniu
| Przykładsiłapotencjał | |
Przykład 2.2
Skończone układy punktów materialnych oddziaływujących wzajemnie siłą grawitacji są potencjalne.
Dla większej przejrzystości przeprowadzimy rozumowanie dla układu trzech punktów o masach ![]() Sytuacja ogólna różni się tylko większą komplikacją zapisu.
Sytuacja ogólna różni się tylko większą komplikacją zapisu.
Zgodnie z punktem (4) ze Wstępu w Wykładzie 1 potraktujemy nasz układ jako punkt ![]() w
w ![]() Wtedy
Wtedy ![]() gdzie
gdzie ![]() jest położeniem
jest położeniem ![]() -tego punktu. Podobnie
-tego punktu. Podobnie ![]()
jest siłą działającą na ![]() której potencjał chcemy wyznaczyć, natomiast
której potencjał chcemy wyznaczyć, natomiast ![]() jest wtedy siłą działającą na
jest wtedy siłą działającą na ![]() ty punkt. Zgodnie z (1.9)otrzymamy
ty punkt. Zgodnie z (1.9)otrzymamy
Twierdzimy, że ta siła jest potencjalna w ![]() . Istotnie zauważmy, że w
. Istotnie zauważmy, że w ![]() funkcja
funkcja
ma ![]() równy
równy
Zatem ![]() Zauważmy też, że dla ustalonego wektora
Zauważmy też, że dla ustalonego wektora ![]()
Wynika stąd, że siła ![]() jest w
jest w ![]() -gradientem funkcji
-gradientem funkcji