Zagadnienia
3. Energia mechaniczna
3.1. Energia kinetyczna i energia całkowita.
Odwróćmy sytuację omawianą w Ćwiczeniu 2.1. Niech droga ![]() teraz będzie torem saneczkowym, biegnącym z punktu B do punktu A. Wyobraźmy sobie, że sanki ruszają z punktu B z prędkością 0. W kolejnych chwilach ich energia potencjalna związana z aktualną pozycją maleje i jednocześnie pojawia się, zależna od prędkości sanek i ich masy, energia ruchu czyli energia kinetyczna. Dowodem na jej istnienie są skutki ewentualnego zderzenia sanek z przedmiotem pozostającym na torze ich ruchu. Łatwo zauważyć, że energia kinetyczna nie zależy od położenia sanek ani od kierunku i zwrotu ich prędkości. (Tor zbudowany identycznie, ale znajdujący się w innym miejscu i inaczej zorientowany, spowodowałby takie same skutki zderzenia). Nietrudno też ustalić, że energia kinetyczna jest proporcjonalna do masy poruszającego się ciała. Oznaczmy energię kinetyczną literą
teraz będzie torem saneczkowym, biegnącym z punktu B do punktu A. Wyobraźmy sobie, że sanki ruszają z punktu B z prędkością 0. W kolejnych chwilach ich energia potencjalna związana z aktualną pozycją maleje i jednocześnie pojawia się, zależna od prędkości sanek i ich masy, energia ruchu czyli energia kinetyczna. Dowodem na jej istnienie są skutki ewentualnego zderzenia sanek z przedmiotem pozostającym na torze ich ruchu. Łatwo zauważyć, że energia kinetyczna nie zależy od położenia sanek ani od kierunku i zwrotu ich prędkości. (Tor zbudowany identycznie, ale znajdujący się w innym miejscu i inaczej zorientowany, spowodowałby takie same skutki zderzenia). Nietrudno też ustalić, że energia kinetyczna jest proporcjonalna do masy poruszającego się ciała. Oznaczmy energię kinetyczną literą ![]() . Bardziej precyzyjne pomiary np. skutków ilościowych zderzenia a także względy matematyczne, powodują, że jako miarę energii kinetycznej przyjmujemy wyrażenie:
. Bardziej precyzyjne pomiary np. skutków ilościowych zderzenia a także względy matematyczne, powodują, że jako miarę energii kinetycznej przyjmujemy wyrażenie:
| (3.1) |
Zdefiniujemy następnie całkowitą energię mechaniczną ciała jako
| (3.2) |
Faktem o podstawowym znaczeniu (a także pokazującym trafność definicji ![]() ) jest
) jest
Twierdzenie 3.1
Dla ruchu pod wpływem siły potencjalnej energia całkowita jest stała w trakcie ruchu.
Wystarczy pokazać, że jeżeli ![]() jest krzywą ruchu, tj. rozwiązaniem równania
jest krzywą ruchu, tj. rozwiązaniem równania
to
| (3.3) |
Istotnie,
![=\frac{1}{2}m\Big[\langle\ddot{\gamma}(t),\dot{\gamma}(t)\rangle+\langle\dot{\gamma}(t)\rangle,\ddot{\gamma}(t)\Big]+\sum _{{l=1}}^{{n}}\frac{\partial U}{\partial x_{i}}(\gamma(t))\cdot\dot{\gamma}_{i}(t)=](wyklady/mmk/mi/mi244.png) |
Ćwiczenie 3.1
Pokazać, że energia całkowita sanek zjeżdżających torem od punktu B do A pozostaje stała w trakcie ruchu.
Niech ![]() oznacza masę sanek oraz niech
oznacza masę sanek oraz niech ![]() będzie ”historią” naszego ślizgu od B do A. Zauważmy, że:
będzie ”historią” naszego ślizgu od B do A. Zauważmy, że:
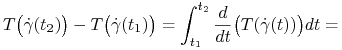 |
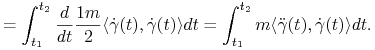 |
Ponieważ nasz tor ruchu jest zmieniony w stosunku do toru ruchu pod wpływem siły ![]() (porównaj Ćwiczenie 2.1), musi działać jakaś dodatkowa siła
(porównaj Ćwiczenie 2.1), musi działać jakaś dodatkowa siła ![]() zaginająca ten tor tak, że
zaginająca ten tor tak, że ![]() . Siłę
. Siłę ![]() nazywamy siłą reakcji więzów. Założymy, że dla każdego punktu toru siła
nazywamy siłą reakcji więzów. Założymy, że dla każdego punktu toru siła ![]() w tym punkcie jest prostopadła do krzywej
w tym punkcie jest prostopadła do krzywej ![]() a więc, że
a więc, że ![]() dla każdego
dla każdego ![]() . Wtedy (porównaj dowód implikacji
. Wtedy (porównaj dowód implikacji ![]() w Twierdzeniu 2.1.
w Twierdzeniu 2.1.
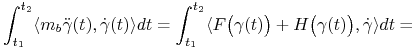 |
![=\int _{{t_{1}}}^{{t_{2}}}\langle F\big(\gamma(t)\big),\dot{\gamma}(t)\rangle dt=-\Big[U\big(\gamma(t_{2})\big)-U\big(\gamma(t_{1})\big)\Big]=U\big(\gamma(t_{1})\big)-U\big(\gamma(t_{2})\big).](wyklady/mmk/mi/mi186.png) |
Otrzymujemy w rezultacie związek
czyli
Zwróćmy uwagę, że krzywa ruchu nie jest identyczna z torem ruchu swobodnego, więc Ćwiczenie 3.1 nie wynika bezpośrednio z Twierdzenia (3.1). Omówienie sytuacji, kiedy punkt materialny jest zmuszony do pozostawania na powierzchni większego wymiaru (jak w przypadku np. kulki metalowej znajdującej się w sferycznym naczyniu w polu grawitacyjnym), odłożymy do momentu wprowadzenia wariacyjnego opisu ruchu.
∎3.2. Przestrzeń konfiguracyjna i przestrzeń fazowa oraz całki pierwsze układów mechanicznych.
Przedyskutujemy teraz niektóre skutki zaobserwowanej w Twierdzeniu (3.1) niezmienniczości energii całkowitej. Rozważmy ogólny układ potencjalny. Jego ruch opisany jest układem równań Newtona.
| (3.4) |
Każde jego rozwiązanie jest związane wzajemnie jednoznacznie z warunkami początkowymi. Te z kolei wyznaczają wartość ![]() energii całkowitej w chwili początkowej. Warunek stałości energii mający postać
energii całkowitej w chwili początkowej. Warunek stałości energii mający postać
prowadzi do równania
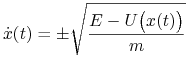 |
(3.5) |
wyznaczającego możliwe ewolucje naszego układu mechanicznego przy danym poziomie ![]() energii całkowitej. Równanie (3.5) jest pierwszego rzędu i na ogół łatwiej je rozwiązać niż oryginalny układ (3.4).
energii całkowitej. Równanie (3.5) jest pierwszego rzędu i na ogół łatwiej je rozwiązać niż oryginalny układ (3.4).
Okazuje się, że poza potencjalnością występujących sił, można podać wiele innych warunków ”symetrii” implikujących pojawienie się innych, niż energia całkowita funkcji zależnych od prędkości i położeń, które pozostają stałe w trakcie ruchu. Funkcje takie nazywa się całkami pierwszymi ruchu. Nazwa ta jest motywowana analogią teorioliczbową.
Warunek ich stałości prowadzi, podobnie jak w przypadku energii całkowitej, do uproszczenia równań ruchu. Dla uzyskania przejrzystości dalszych rozważań wprowadzimy następujące uzupełnienia naszego modelu matematycznego.
Definicja 3.1
Rozważmy układ mechaniczny ![]() Zbiór wszystkich potencjalnie możliwych położeń chwilowych tego układu nazwiemy przestrzenią konfiguracyjną układu i będziemy oznaczać
Zbiór wszystkich potencjalnie możliwych położeń chwilowych tego układu nazwiemy przestrzenią konfiguracyjną układu i będziemy oznaczać ![]() (lub
(lub ![]() , jeżeli wiadomo, o jakim układzie mowa).
, jeżeli wiadomo, o jakim układzie mowa).
Komentarz Poprawne matematycznie podejście wymagałoby w tym momencie założenia u czytelnika znajomości pojęcia rozmaitości różniczkowej a następnie pojęcia wiązki stycznej do takiej rozmaitości. Ponieważ prezentowany kurs nie zależy w istotny sposób od tych pojęć , a rozpatrywane przykłady mogą służyć jako ich ilustracja i nie wymagają ogólnej teorii, zdecydowaliśmy się jedynie zasygnalizować czytelnikowi potrzebę jej poznania, starając się w miarę możliwości unikać komplikacji geometrycznych.
Przykład 3.1
(a) Niech ![]() lub składa się z punktu materialnego o masie
lub składa się z punktu materialnego o masie ![]() połączonego sztywnym nieważkim prętem o długości
połączonego sztywnym nieważkim prętem o długości ![]() z nieruchomym punktem
z nieruchomym punktem ![]() . Wtedy
. Wtedy ![]() jest sferą dwuwymiarową w
jest sferą dwuwymiarową w ![]() o środku
o środku ![]() i promieniu
i promieniu ![]()
(b) Niech ![]() składa się z dwóch punktów poruszających się swobodnie w
składa się z dwóch punktów poruszających się swobodnie w ![]() , ale związanych ze sobą sztywnym, nieważkim prętem o długości
, ale związanych ze sobą sztywnym, nieważkim prętem o długości ![]() . Wtedy przyjmując dowolnie położenie pierwszego punktu o współrzędnych
. Wtedy przyjmując dowolnie położenie pierwszego punktu o współrzędnych ![]() dostajemy warunek na współrzędne drugiego punktu
dostajemy warunek na współrzędne drugiego punktu ![]() w formie:
w formie:
| (3.6) |
Dostajemy więc ![]() jako pięciowymiarową podrozmaitość w
jako pięciowymiarową podrozmaitość w ![]() opisaną warunkiem (3.6)
opisaną warunkiem (3.6)
(c)Przestrzeń konfiguracyjna układu ![]() - punktów jest równa
- punktów jest równa ![]() .
.
Definicja 3.2
Wymiarem układu ![]() nazwiemy wymiar jego przestrzeni konfiguracyjnej.
nazwiemy wymiar jego przestrzeni konfiguracyjnej.
Definicja 3.3
Przestrzenią fazową układu mechanicznego ![]() nazwiemy zbiór wszystkich potencjalnie możliwych par, składających się z położenia chwilowego i odpowiadającej temu położeniu prędkości chwilowej. Przestrzeń fazową układu
nazwiemy zbiór wszystkich potencjalnie możliwych par, składających się z położenia chwilowego i odpowiadającej temu położeniu prędkości chwilowej. Przestrzeń fazową układu ![]() będziemy oznaczać
będziemy oznaczać ![]()
Komentarz Przestrzeń fazowa ![]() ma strukturę wiązki stycznej, której bazą jest przestrzeń konfiguracyjna
ma strukturę wiązki stycznej, której bazą jest przestrzeń konfiguracyjna ![]()
Przykład 3.2
Dla układów ![]() i
i ![]() z Przykładów 3.1 jako ich przestrzenie fazowe otrzymamy odpowiednio: wiązkę styczną do
z Przykładów 3.1 jako ich przestrzenie fazowe otrzymamy odpowiednio: wiązkę styczną do ![]() wiązkę styczną do
wiązkę styczną do ![]() i wiązkę styczną do
i wiązkę styczną do ![]()
Definicja 3.4
Niech dany będzie układ mechaniczny ![]() Wraz z krzywą ruchu
Wraz z krzywą ruchu ![]() rozważać będziemy jej kanoniczne rozszerzenie do przestrzeni fazowej, które oznaczać będziemy
rozważać będziemy jej kanoniczne rozszerzenie do przestrzeni fazowej, które oznaczać będziemy ![]() (dla każdego
(dla każdego ![]() leży w przestrzeni stycznej do
leży w przestrzeni stycznej do ![]() w punkcie
w punkcie ![]() . Funkcję (skalarną lub wektorową)
. Funkcję (skalarną lub wektorową) ![]() nazwiemy całką pierwszą
nazwiemy całką pierwszą ![]() , jeżeli funkcja złożona
, jeżeli funkcja złożona ![]() jest stała.
jest stała.
Poza układami opisującymi ruch kilku punktów w ![]() , rozważać będziemy fikcyjne układy kilku punktów w
, rozważać będziemy fikcyjne układy kilku punktów w ![]() . Ma to sens formalny, a rozważanie takich układów (na ogół dla
. Ma to sens formalny, a rozważanie takich układów (na ogół dla ![]() ) umożliwia lepsze zrozumienie układów fizycznych, usuwając, często nieistotne, trudności rachunkowe, występujące w większym wymiarze.
) umożliwia lepsze zrozumienie układów fizycznych, usuwając, często nieistotne, trudności rachunkowe, występujące w większym wymiarze.
3.3. Układy 1-wymiarowe i ich obrazy fazowe.
Wykorzystując prawo zachowania energii całkowitej, przeprowadzimy dyskusję układu 1-wymiarowego z zadanym potencjałem ![]() .
Rozważmy określony dla
.
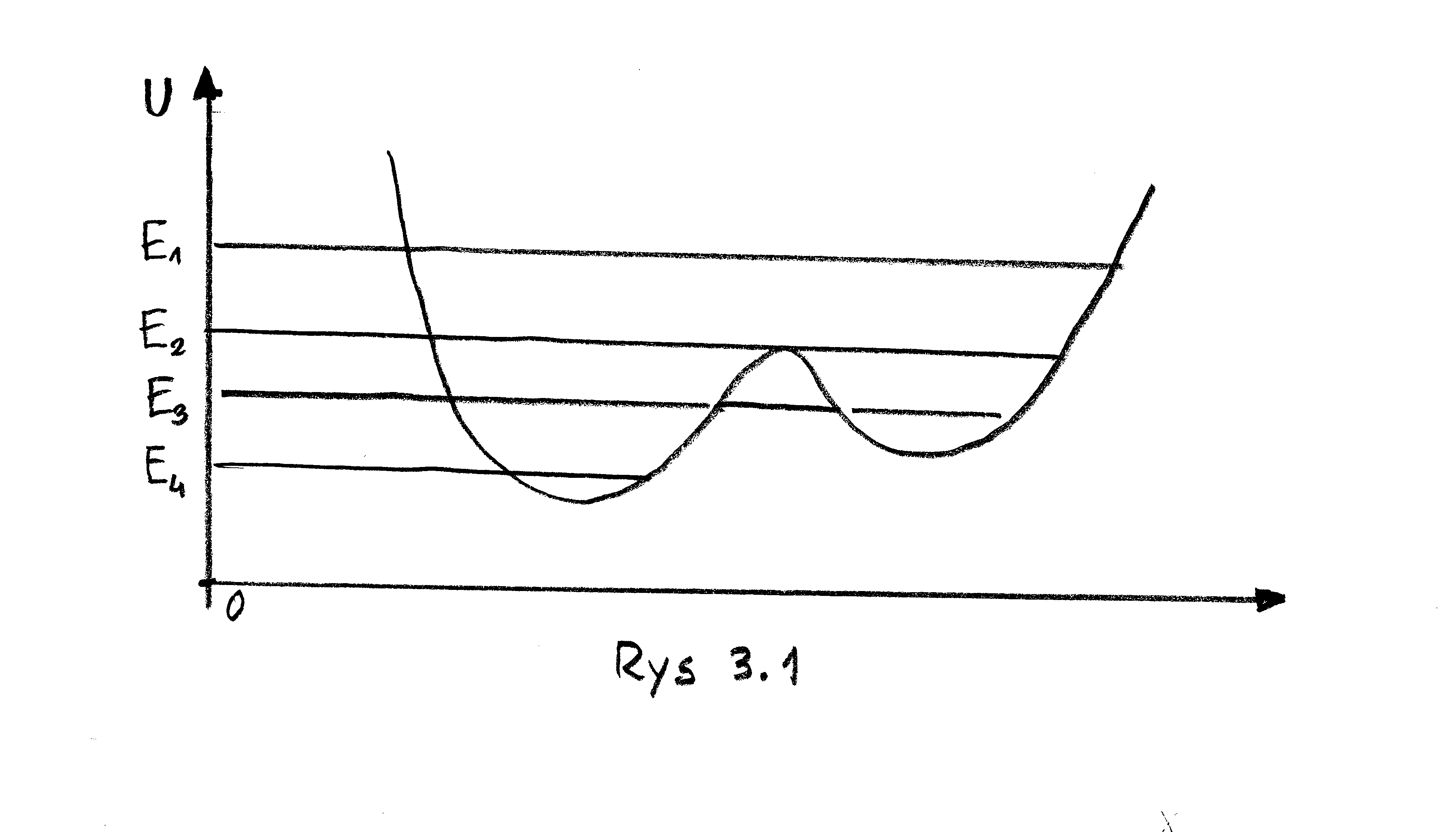
Rozważmy określony dla ![]() potencjał, którego wykres przedstawia rys.3.1.
potencjał, którego wykres przedstawia rys.3.1.
Warunek stałości energii całkowitej ![]() , (gdzie
, (gdzie ![]() a
a ![]() oznacza prędkość w punkcie
oznacza prędkość w punkcie ![]() ) wyznacza krzywe - poziomice tej energii.
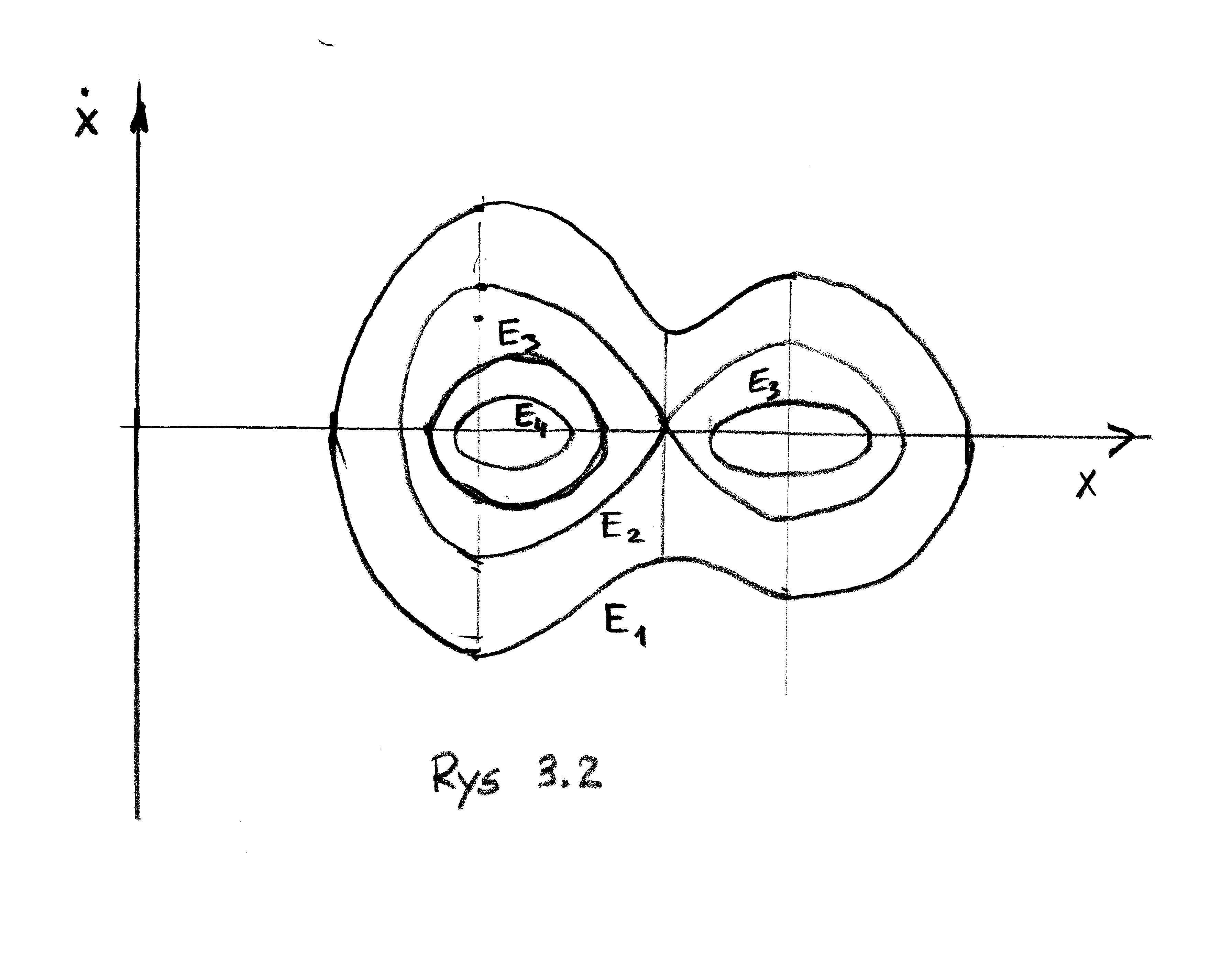
Krzywe takie odpowiadające wartościom
) wyznacza krzywe - poziomice tej energii.
Krzywe takie odpowiadające wartościom ![]() podaje rysunek 3.2.
Są one opisane wzorem
podaje rysunek 3.2.
Są one opisane wzorem
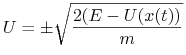 |
(3.7) |
Z rysunku 3.2 można odczytać wiele własności ruchu przy danym potencjale i zadanej wartości energii całkowitej.