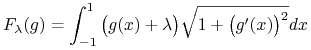Zagadnienia
7. Rachunek wariacyjny, równania Eulera.
7.1. Wprowadzenie
Przedmiotem rachunku wariacyjnego są warunki ekstremalności funkcji (tradycyjnie nazywanych funkcjonałami), których dziedziną są rodziny obiektów geometrycznych (np. krzywe, powierzchnie) a wartości należą do ![]() Styk prezentowanej w tym wykładzie tematyki z rachunkiem wariacyjnym jest ograniczony do specjalnej sytuacji, którą charakteryzują poniższe założenia:
Styk prezentowanej w tym wykładzie tematyki z rachunkiem wariacyjnym jest ograniczony do specjalnej sytuacji, którą charakteryzują poniższe założenia:
(A) Dziedziną badanego funkcjonału ![]() jest rodzina
jest rodzina ![]() krzywych o wartościach w
krzywych o wartościach w ![]() określonych na wspólnym przedziale
określonych na wspólnym przedziale ![]() i mających wspólny początek i wspólny koniec. Wszystkie krzywe z
i mających wspólny początek i wspólny koniec. Wszystkie krzywe z ![]() są ustalonej klasy gładkości.
są ustalonej klasy gładkości.
(B) Rozważane funkcjonały mają postać
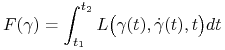 |
(7.1) |
gdzie ![]() a
a ![]() jest klasy
jest klasy ![]()
(C) Rozważanym problemem jest charakteryzacja punktów stacjonarnych funkcjonału ![]() tj. takich
tj. takich ![]() , że
, że
| (7.2) |
(zob. Uwaga 7.1).
Użycie określenia funkcjonał dla funkcji ![]() miało zapewne na celu ułatwienie wysłowień, bo argumentami
miało zapewne na celu ułatwienie wysłowień, bo argumentami ![]() są także funkcje. Konwencję tę podjęła też powstała później analiza funkcjonalna.
są także funkcje. Konwencję tę podjęła też powstała później analiza funkcjonalna.
Uwaga 7.1
Warunek (7.2) wymaga komentarza: dziedzina ![]() funkcjonału (7.1) jest podprzestrzenią afiniczną przestrzeni liniowej
funkcjonału (7.1) jest podprzestrzenią afiniczną przestrzeni liniowej ![]() , składającej się z wszystkich krzywych tej samej co dla
, składającej się z wszystkich krzywych tej samej co dla ![]() klasy gładkości, określonych na
klasy gładkości, określonych na ![]() Istotnie, każdą krzywą
Istotnie, każdą krzywą ![]() można jednoznacznie przedstawić w formie
można jednoznacznie przedstawić w formie ![]() gdzie
gdzie ![]() jest ustaloną krzywą z
jest ustaloną krzywą z ![]() a
a ![]() gdzie
gdzie ![]() jest podprzestrzenią liniową
jest podprzestrzenią liniową ![]() Elementy
Elementy ![]() będziemy nazywali wariacjami. Wracając do (7.2) ustalając
będziemy nazywali wariacjami. Wracając do (7.2) ustalając ![]() możemy krzywe
możemy krzywe ![]() zapisać w postaci
zapisać w postaci ![]() Zatem
Zatem ![]() Wprowadzając
Wprowadzając ![]() gdzie teraz
gdzie teraz ![]() jest funkcjonałem na
jest funkcjonałem na ![]() redukujemy pytanie o stacjonarność
redukujemy pytanie o stacjonarność ![]() dla
dla ![]() do pytania, czy
do pytania, czy ![]()
Część rachunku wariacyjnego dotycząca założeń ![]() przypomina więc fragment klasycznej analizy, dotyczący warunku koniecznego istnienia ekstremum.
Sytuacja w rachunku wariacyjnym różni się tym, że dziedzina badanej funkcji jest nieskończenie wymiarowa. Za to same funkcje - ”funkcjonały” - są bardzo specjalnej postaci. Schemat uwarunkowany założeniami
przypomina więc fragment klasycznej analizy, dotyczący warunku koniecznego istnienia ekstremum.
Sytuacja w rachunku wariacyjnym różni się tym, że dziedzina badanej funkcji jest nieskończenie wymiarowa. Za to same funkcje - ”funkcjonały” - są bardzo specjalnej postaci. Schemat uwarunkowany założeniami ![]() jest krokiem wstępnym, poza który w zasadzie nie wyjdziemy. Jedynym wyjątkiem jest uogólnienie warunku
jest krokiem wstępnym, poza który w zasadzie nie wyjdziemy. Jedynym wyjątkiem jest uogólnienie warunku ![]() do takiego, w którym
do takiego, w którym ![]() jest zbiorem krzywych przyjmujących swoje wartości w podrozmaitościach
jest zbiorem krzywych przyjmujących swoje wartości w podrozmaitościach ![]() Ta sytuacja pojawia się przy badaniu układów z więzami.
Ta sytuacja pojawia się przy badaniu układów z więzami.
7.2. Przykłady zagadnień wariacyjnych.
Niech ![]() będzie rodziną krzywych klasy
będzie rodziną krzywych klasy ![]() określonych na [0,1] i przyjmujących wartości w
określonych na [0,1] i przyjmujących wartości w ![]() Załóżmy, że wszystkie nasze krzywe zaczynają się w punkcie (0, 1) a kończą w (1,0). Rozpatrzmy na
Załóżmy, że wszystkie nasze krzywe zaczynają się w punkcie (0, 1) a kończą w (1,0). Rozpatrzmy na ![]() stałe pole wektorowe
stałe pole wektorowe
| (7.3) |
Problem 7.1
Wśród krzywych rodziny ![]() wskazać taką, żeby ruch po niej bez tarcia i pod wpływem pola
wskazać taką, żeby ruch po niej bez tarcia i pod wpływem pola ![]() zaczynający się od prędkości zero trwał możliwie jak najkrócej.
Problem ten jest nazywany zagadnieniem krzywej najszybszego spadku (brachistochrony) z greckiego brachistos- najkrótszy, chronos - czas.
zaczynający się od prędkości zero trwał możliwie jak najkrócej.
Problem ten jest nazywany zagadnieniem krzywej najszybszego spadku (brachistochrony) z greckiego brachistos- najkrótszy, chronos - czas.
Uwaga 7.2
Ponieważ chodzi nam raczej o wprowadzenie do metod rachunku wariacyjnego niż o rozstrzygnięcie ogólnego pytania, ograniczymy się do krzywych, których zbiorem wartości są punkty o postaci ![]() dla
dla ![]() gdzie funkcja
gdzie funkcja ![]() jest klasy
jest klasy ![]() malejąca oraz
malejąca oraz ![]() i
i ![]() Zatem
Zatem
| (7.4) |
Założymy ponadto, że ![]() ,
, ![]() i
i ![]() dla
dla ![]() Dowód, że przy rozwiązywaniu Problemu 7.1 można się ograniczyć do krzywych o postaci (7.4) i rosnących funkcji
Dowód, że przy rozwiązywaniu Problemu 7.1 można się ograniczyć do krzywych o postaci (7.4) i rosnących funkcji ![]() , pozostawimy czytelnikowi.
, pozostawimy czytelnikowi.
Dyskusja wstępna.
Zauważmy, że siła (7.3) spełnia warunek ![]() przy
przy![]() Zaczniemy od wyprowadzenia wzoru na czas potrzebny do przebycia ustalonej krzywej. Bez założenia, że
Zaczniemy od wyprowadzenia wzoru na czas potrzebny do przebycia ustalonej krzywej. Bez założenia, że ![]() jest malejąca, formuła ta mogłaby dać nieskończony czas na przejście, co skomplikowałoby formalnie nasze wywody.
Zgodnie z Ćwiczeniem 3.1, w ruchu bez tarcia po zadanej krzywej pod wpływem pola potencjalnego, jest zachowywana energia całkowita
jest malejąca, formuła ta mogłaby dać nieskończony czas na przejście, co skomplikowałoby formalnie nasze wywody.
Zgodnie z Ćwiczeniem 3.1, w ruchu bez tarcia po zadanej krzywej pod wpływem pola potencjalnego, jest zachowywana energia całkowita ![]() gdzie
gdzie ![]() jest energią kinetyczną o postaci
jest energią kinetyczną o postaci
(przyjmujemy, że masa poruszającego się punktu wynosi 1). Ponieważ dla krzywej (7.4) zachodzi
| (7.5) |
otrzymamy:
| (7.6) |
Z uwagi na to, że ![]() musi być
musi być ![]() zatem
zatem
a ponieważ ![]() otrzymamy
otrzymamy
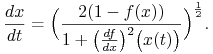 |
Ponieważ chcemy znależć czas przebycia krzywej, napiszmy dla ![]()
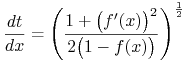 |
skąd ![]() otrzymamy w formie
otrzymamy w formie
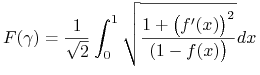 |
(7.7) |
Tak więc otrzymaliśmy funkcjonał (7.1) z funkcją ![]() o postaci
o postaci
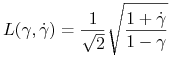 |
gdzie rolę zmiennej ![]() pełni zmienna
pełni zmienna ![]() przebiegająca przedział [0,1].
Drugie zadanie ”zagadnienie krzywej łańcuchowej” ma charakter statyczny. Przyjmijmy, że w
przebiegająca przedział [0,1].
Drugie zadanie ”zagadnienie krzywej łańcuchowej” ma charakter statyczny. Przyjmijmy, że w ![]() jest dane pole wektorowe we
jest dane pole wektorowe we ![]() i że w każdym interesującym nas punkcie siła działająca na masę
i że w każdym interesującym nas punkcie siła działająca na masę ![]() wynosi
wynosi ![]() Wtedy energia potencjalna punktu o masie
Wtedy energia potencjalna punktu o masie ![]() jest
jest ![]() W polu tym zawieszamy idealnie giętką linę (łańcuch) o stałej liniowej gęstości masy 1 i długości
W polu tym zawieszamy idealnie giętką linę (łańcuch) o stałej liniowej gęstości masy 1 i długości ![]() Punktami zawieszenia liny będą
Punktami zawieszenia liny będą ![]() i
i ![]()
Założenie
Przyjmiemy jako założenie, że zwisająca lina przyjmuje kształt, przy którym suma (całka) energii potencjalnych wszystkich jej punktów zwana dalej ”potencjałem sumarycznym” jest możliwie najmniejsza.
Problem 7.2
Opisać krzywą zwisu liny.
Dyskusja wstępna.
Podobnie, jak poprzednio (por. Uwaga 7.2), przyjmiemy, że krzywa zwisu liny opisana jest jako wykres funkcji ![]() należacej do zbioru
należacej do zbioru ![]() funkcji różniczkowalnych o ciągłej pochodnej na przedziale [-1,1] i przyjmujących wartość 0 na końcach przedziału.
funkcji różniczkowalnych o ciągłej pochodnej na przedziale [-1,1] i przyjmujących wartość 0 na końcach przedziału.
Z przedstawionych powyżej założeń wynika, że odcinek ![]() liny znajdujący się na wysokości
liny znajdujący się na wysokości ![]() ma energię potencjalną równą
ma energię potencjalną równą ![]() gdzie
gdzie
Zatem, ”potencjał sumaryczny” ma postać:
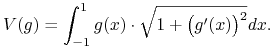 |
(7.8) |
Tego typu funkcja ![]() nie byłaby oczywiście ograniczona z dołu na
nie byłaby oczywiście ograniczona z dołu na ![]() gdyby nie dodatkowy warunek, że długość liny wynosi
gdyby nie dodatkowy warunek, że długość liny wynosi ![]() Warunek ten ma postać
Warunek ten ma postać ![]() gdzie
gdzie
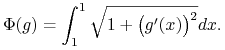 |
(7.9) |
Naszym zadaniem jest więc znalezienie punktów krytycznych funkcjonału ![]() na poziomicy
na poziomicy
Podobnie, jak przy badaniu ekstremów warunkowych w analizie, rozwiążemy ten problem metodą mnożników Lagrange'a.
Polega ona na rozpatrzeniu rodziny funkcjonałów ![]() o postaci
o postaci
gdzie parametr ![]() Dla każdego z tych funkcjonałów szukamy punktów krytycznych leżących na
Dla każdego z tych funkcjonałów szukamy punktów krytycznych leżących na ![]() Wyjaśnienie tego jest następujące:
Wyjaśnienie tego jest następujące:
Jeżeli ![]() dla
dla ![]() to z uwagi na fakt, że różniczka
to z uwagi na fakt, że różniczka ![]() ograniczona do przestrzeni stycznej w
ograniczona do przestrzeni stycznej w ![]() do
do ![]() jest zerowa, warunek
jest zerowa, warunek ![]() pociąga, że
pociąga, że ![]() na tejże przestrzeni stycznej. Jednocześnie właściwy dobór
na tejże przestrzeni stycznej. Jednocześnie właściwy dobór ![]() umożliwia uzyskanie warunku
umożliwia uzyskanie warunku ![]() także na przestrzeni prostopadłej do
także na przestrzeni prostopadłej do ![]() w punkcie
w punkcie ![]()
Podsumowując: pierwszym krokiem do rozwiązania Problemu 7.2 jest znalezienie należących do ![]() punktów krytycznych funkcjonałów
punktów krytycznych funkcjonałów
7.3. Punkty krytyczne i równania Eulera
Będziemy poszukiwać warunków, przy których krzywa ![]() jest punktem krytycznym funkcjonału
jest punktem krytycznym funkcjonału
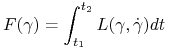 |
(7.12) |
Pisząc ![]() redukujemy nasz problem do pytania czy funkcjonał
redukujemy nasz problem do pytania czy funkcjonał
| (7.13) |
ma w punkcie ![]() punkt krytyczny. ( Y jest tutaj przestrzenią liniową wariacji - zob. Uwagę 7.1.)
punkt krytyczny. ( Y jest tutaj przestrzenią liniową wariacji - zob. Uwagę 7.1.)
Wyposażmy ![]() w w strukturę przestrzeni Banacha, wprowadzając
w w strukturę przestrzeni Banacha, wprowadzając ![]() normę:
normę:
| (7.14) |
gdzie ![]() oznacza normę euklidesową w
oznacza normę euklidesową w ![]() Zamierzamy zapisać
Zamierzamy zapisać ![]() w postaci
w postaci
| (7.15) |
gdzie ![]() jest ciągłą w normie (7.14) operacją liniową, natomiast
jest ciągłą w normie (7.14) operacją liniową, natomiast ![]() spełnia warunek:
spełnia warunek:
| (7.16) |
Definicja 7.1
Powiemy, że funkcjonał (7.12) jest różniczkowalny w ![]() (lub, że (7.13) jest różniczkowalny w 0), jeżeli przestawienie (7.15) z warunkiem (7.16) jest możliwe. Operacja liniowa
(lub, że (7.13) jest różniczkowalny w 0), jeżeli przestawienie (7.15) z warunkiem (7.16) jest możliwe. Operacja liniowa ![]() jest wtedy wyznaczona jednoznacznie i nazywa się różniczką
jest wtedy wyznaczona jednoznacznie i nazywa się różniczką ![]() w 0 (lub różniczką
w 0 (lub różniczką ![]() w
w ![]() ). Powiemy, że
). Powiemy, że ![]() jest punktem krytycznym
jest punktem krytycznym ![]() jeżeli
jeżeli ![]() (tj.
(tj. ![]() dla każdego
dla każdego ![]()
Twierdzenie 7.1
Jeżeli ![]() jest postaci (7.12), gdzie funkcja
jest postaci (7.12), gdzie funkcja ![]() jest klasy
jest klasy ![]() to dla każdego
to dla każdego ![]() istnieje
istnieje ![]() Na to, aby krzywa
Na to, aby krzywa ![]() była punktem krytycznym
była punktem krytycznym ![]() potrzeba i wystarcza, by spełniała ona układ równań :
potrzeba i wystarcza, by spełniała ona układ równań :
| (7.17) |
Równania powyższe noszą nazwę równań Eulera.
Ustalimy najpierw możliwą postać operacji ![]() , występującej w formule (7.15).
, występującej w formule (7.15).
Oznaczmy zmienne, od których zależy ![]() jako
jako ![]() Wtedy zgodnie ze wzorem Taylora dla przyrostu
Wtedy zgodnie ze wzorem Taylora dla przyrostu ![]() zachodzi
zachodzi
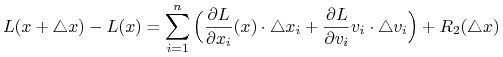 |
gdzie
| (7.18) |
gdy ![]() dąży do zera, a
dąży do zera, a ![]() jest normą euklidesową w
jest normą euklidesową w ![]()
Podstawiając ![]() oraz
oraz ![]() przy ustalonym
przy ustalonym ![]() i dla
i dla ![]() oraz wycałkowując po
oraz wycałkowując po ![]() otrzymamy, zgodnie z (7.13):
otrzymamy, zgodnie z (7.13):
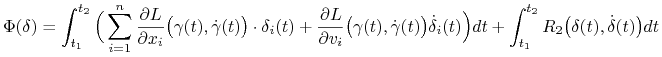 |
(7.19) |
Część pierwsza, po prawej stronie równości (7.19) zależy liniowo od ![]() i przyjmujemy ją jako
i przyjmujemy ją jako ![]() Także odpowiednio przyjmujemy
Także odpowiednio przyjmujemy
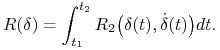 |
(7.20) |
Mamy wtedy
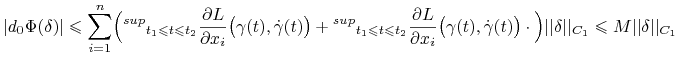 |
gdzie ![]() jest stałą zależną
jest stałą zależną ![]() Zatem
Zatem ![]() jest ciągłym funkcjonałem liniowym.
Pokażemy, że reszta
jest ciągłym funkcjonałem liniowym.
Pokażemy, że reszta ![]() spełnia warunek (7.16).
Zauważmy najpierw, że dla każdego ustalonego
spełnia warunek (7.16).
Zauważmy najpierw, że dla każdego ustalonego ![]()
Więc na mocy (7.14), (7.18) i (7.20) otrzymamy:
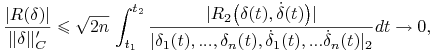 |
przy ![]()
Przejdźmy do wyprowadzenia równań (7.17).
Warunek ![]() oznacza, że dla każdego
oznacza, że dla każdego ![]() zachodzi:
zachodzi:
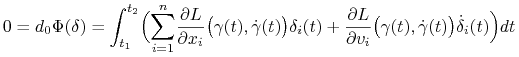 |
Całkując przez części drugie człony składników sumy oraz uwzględniając, że ![]() otrzymamy:
otrzymamy:
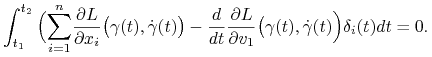 |
(7.21) |
Przyjmując jako ![]() kolejno krzywe o postaci
kolejno krzywe o postaci 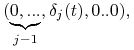 gdzie
gdzie ![]() może być dowolną funkcją różniczkowalną taką, że z
może być dowolną funkcją różniczkowalną taką, że z ![]() otrzymamy
otrzymamy ![]() niezależnych warunków
niezależnych warunków
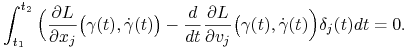 |
(7.22) |
![]()
Nietrudne rozumowanie pokazuje, że ![]() ty warunek (7.22) jest równoważny
ty warunek (7.22) jest równoważny ![]() temu równaniu Eulera. Odwrotnie: spełnienie równań Eulera daje równania (7.22) a te przez wysumowanie warunek (7.21), z którego wynika z kolei, że
temu równaniu Eulera. Odwrotnie: spełnienie równań Eulera daje równania (7.22) a te przez wysumowanie warunek (7.21), z którego wynika z kolei, że ![]()
Uwaga 7.3
Chcąc uniknąć wprowadzania zmiennych ![]() oraz
oraz ![]() zapisuje się równania, utożsamiając
zapisuje się równania, utożsamiając ![]() z
z ![]() oraz
oraz ![]() z
z ![]() w postaci (7.17).
w postaci (7.17).
7.4. Przykłady równań Eulera.
Na zakończenie napiszemy równania Eulera dla zagadnienia brachistochrony i zagadnienia krzywej łańcuchowej.
Przykład 7.1
Równanie Eulera dla zagadnienia brachistochomy.
Mamy znaleźć funkcję ![]() argumentu
argumentu ![]() , który pełni rolę zmiennej
, który pełni rolę zmiennej ![]() w równianiach Eulera (zobacz sformułowanie Twierdzenia 7.1). Będziemy pisać
w równianiach Eulera (zobacz sformułowanie Twierdzenia 7.1). Będziemy pisać ![]() zamiast
zamiast ![]() oraz
oraz ![]() zamiast
zamiast ![]() . Nasza funkcja Lagrange'a ma zatem postać:
. Nasza funkcja Lagrange'a ma zatem postać:
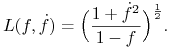 |
Wtedy
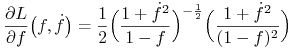 |
oraz
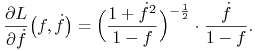 |
Równanie Eulera
przyjmie więc postać
![\frac{1}{2}\Big(\frac{1+(\frac{df}{dx})^{2}}{1-f}\Big)^{{-\frac{1}{2}}}\cdot\frac{1+\big(\frac{df}{dx}\big)^{2}}{(1-f)}^{2}+\frac{d}{dx}\Bigg[\Big(\frac{1+\big(\frac{df}{dx}\big)^{2}}{1-f}\Big)^{{-\frac{1}{2}}}\cdot\frac{\frac{df}{dx}}{1-f}\Bigg]=0](wyklady/mmk/mi/mi662.png) |
(7.23) |
Przykład 7.2
Równanie Eulera dla krzywej łańcuchowej.
Podobnie, jak poprzednio, rolę ![]() w równaniach Eulera pełni zmienna
w równaniach Eulera pełni zmienna ![]() , natomiast zamiast
, natomiast zamiast ![]() napiszemy
napiszemy ![]() a zamiast
a zamiast ![]() napiszemy
napiszemy ![]() Funkcja Lagrange'a z mnożnikiem
Funkcja Lagrange'a z mnożnikiem ![]() ma postać:
ma postać:
Wtedy
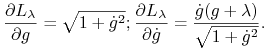 |
Zatem równania Eulera mają postać :
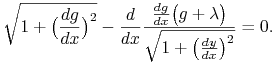 |
(7.24) |