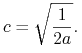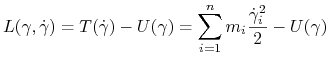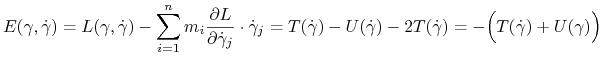Zagadnienia

8.1 Całka pierwsza energii
8.2 Zastosowanie całki energii
- 8.2.1 Krzywa najszybszego spadku
- 8.2.2 Krzywa łańcuchowa
8.3 Równania Eulera - Lagrange'a
8.4 Układy z więzami.

8. Równania Eulera - Lagrange'a

8.1. Całka pierwsza energii

Jak widzieliśmy w punkcie 7.4 poprzedniego wykładu, układy równań Eulera są na ogół zbyt skomplikowane, aby umożliwić dokładny opis poszukiwanych krzywych. Z pomocą przychodzi następujące twierdzenie:

Twierdzenie 8.1

W przypadku, kiedy funkcja Lagrange'a $L$ nie zależy explicite od czasu, funkcja o postaci

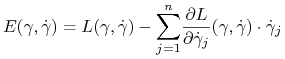$E(\gamma,\dot{\gamma})=L(\gamma,\dot{\gamma})-\displaystyle{\sum _{{j=1}}^{n}}\frac{\partial L}{\partial\dot{\gamma}_{j}}(\gamma,\dot{\gamma})\cdot\dot{\gamma}_{j}$

(8.1)

jest stała na krzywych będących rozwiązaniami układu równań Eulera (7.17). Funkcję (8.1) będziemy nazywać całką energii.

W każdym z równań (7.17) wykonajmy różniczkowanie $\displaystyle\frac{d}{dt}.$ Ponieważ $L$ zależy od $t$ za pośrednictwem $\gamma _{k}$ oraz $\dot{\gamma}_{k}$ $k=1,2,...,n,$ otrzymamy

$\frac{\partial L}{\partial{\gamma}_{j}}(\gamma,\dot{\gamma})-\sum _{{k=1}}^{n}\Bigg[\frac{\partial}{\partial{\gamma}_{k}}\Big(\frac{\partial L}{\partial\dot{\gamma}_{j}}\Big)(\gamma,\dot{\gamma})\cdot\dot{\gamma}_{k}+\frac{\partial}{\partial{\dot{\gamma}}_{k}}\Big(\frac{\partial L}{\partial\dot{\gamma}_{j}}\Big)((\gamma,\dot{\gamma})\cdot\ddot{\gamma}_{k}\Bigg]=0$

(8.2)

$j=1,2,..,n.$ Pomnóżmy $j-$ te równanie 8.2 przez $\dot{\gamma}_{j}$ i dodajmy wszystkie równania stronami. Otrzymamy

$\sum _{{j=1}}^{n}\frac{\partial L}{\partial{\gamma}_{j}}(\gamma,\dot{\gamma})\cdot\dot{\gamma}_{j}-\sum _{{j,k=1}}^{n}\Bigg[\frac{\partial}{\partial{\gamma}_{k}}\Big(\frac{\partial L}{\partial{\dot{\gamma}_{j}}}\Big)(\gamma,\dot{\gamma})\cdot\dot{\gamma}_{j}\dot{\gamma}_{k}+\frac{\partial}{\partial{\gamma\dot{\gamma}_{k}}}\Big(\frac{\partial L}{\partial\dot{\gamma}_{j}}\Big)(\gamma,\dot{\gamma})\cdot\dot{\gamma}_{j}\ddot{\gamma}_{k}\Bigg]=0$

(8.3)

Oznaczmy

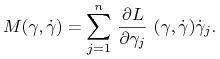$M(\gamma,\dot{\gamma})=\displaystyle{\sum _{{j=1}}^{n}}\ \frac{\partial L}{\partial{\gamma}_{j}}\ (\gamma,\dot{\gamma})\dot{\gamma}_{j}.$

Wtedy, uzupełniając każdy ze składników pierwszej sumy w (8.3) o $\frac{\partial L}{\partial\dot{\gamma}_{j}}(\gamma,\dot{\gamma})\cdot\ddot{\gamma}_{j},$ i odejmując to samo wyrażenie w drugiej części, możemy (8.3) zapisać w postaci

$\displaystyle{\sum _{{j=1}}^{n}}\big(\frac{\partial L}{\partial{\gamma}_{j}}(\gamma,\dot{\gamma})\dot{\gamma}_{j}+\frac{\partial L}{\partial\dot{\gamma}_{j}}(\gamma,\dot{\gamma})\ddot{\gamma}_{j}-\sum _{{k=1}}^{n}\Bigg[\frac{\partial}{\partial{\gamma}_{k}}M(\gamma,\dot{\gamma})\dot{\gamma}_{k}+\frac{\partial}{\partial{\dot{\gamma}_{k}}}M(\gamma,\dot{\gamma})\ddot{\gamma}_{k}+\frac{\partial L}{\partial\dot{\gamma}_{k}}(\gamma,\dot{\gamma})\cdot\ddot{\gamma}_{k}\Bigg]=0$

czyli

$\frac{d}{dt}\big(L(\gamma,\dot{\gamma})-M(\gamma,\dot{\gamma})\big)=0$

co należało wykazać.

∎

8.2. Zastosowanie całki energii

Zastosujemy Twierdzenie (8.1) do wyznaczania postaci krzywej najszybszego spadku oraz krzywej łańcuchowej.

8.2.1. Krzywa najszybszego spadku

W poprzednim wykładzie, dla uproszczenia zapisu przyjęliśmy, że początek krzywej najszybszego spadku znajduje się w (0,1) a koniec w (1,0). czytelnik bez trudu zmodyfikuje otrzymane rozumowanie na przypadek nieco ogólniejszy - początek w (0,a) a koniec w (b,0).W następującym dalej wywodzie traktujmy ten ogólniejszy przypadek. Zgodnie z (7.6) funkcja Lagrange'a w zagadnieniu brachistochrony ma postać:

$\displaystyle{L(y,\dot{y})=\Big(\frac{1+\dot{y}^{2}}{2(a-y)}\Big)^{\frac{1}{2}}}$

zatem całka pierwsza 8.1 wynosi:

$E(y,\dot{y})=\Big(\frac{1+\dot{y}^{2}}{2(a-y)}\Big)^{{\frac{1}{2}}}-\frac{\dot{y}^{2}}{2(a-y)}\cdot\Big(\frac{1+\dot{y}^{2}}{2(a-y)}\Big)^{{-\frac{1}{2}}}$

(8.4)

Gdzie $[0,b]\ni x\rightarrow y(x)\in[0,a]$ jest szukaną funkcją a $\dot{y}$ oznacza $\displaystyle{\frac{dy}{dx}}.$ Przyjmując, że $E(y,\dot{y})=c,$ i mnożąc obie strony otrzymanego w ten sposób równania przez $\displaystyle{\Big(\frac{1+\dot{y}^{2}}{2(a-y)}\Big)^{{\frac{1}{2}}}},$ otrzymamy:

$\frac{1}{2(a-y)(1+\dot{y}^{2})}=c^{2}.$

(8.5)

Wskażemy rozwiązania tego równania. Są one związane ze znanymi z geometrii cykloidami.

Definicja 8.1

Cykloida to krzywa, jaką zakreśla punkt okręgu, toczącego się po prostej.

Przyjmiemy, że promień okręgu wynosi $r$ a prędkość kątowa $\alpha>0.$ Jeżeli założymy, że nasz punkt w chwili zero znajduje się w początku układu współrzędnych oraz, że okrąg toczy się w kierunku dodatnim po $o\overrightarrow{x},$ to przyjmując czas jako parametr, otrzymamy opis parametryczny naszej cykloidy w postaci:

$\qquad{x=r(\alpha t-\sin\alpha t)\atop y=r(1-\cos\alpha t)}$

(8.6)

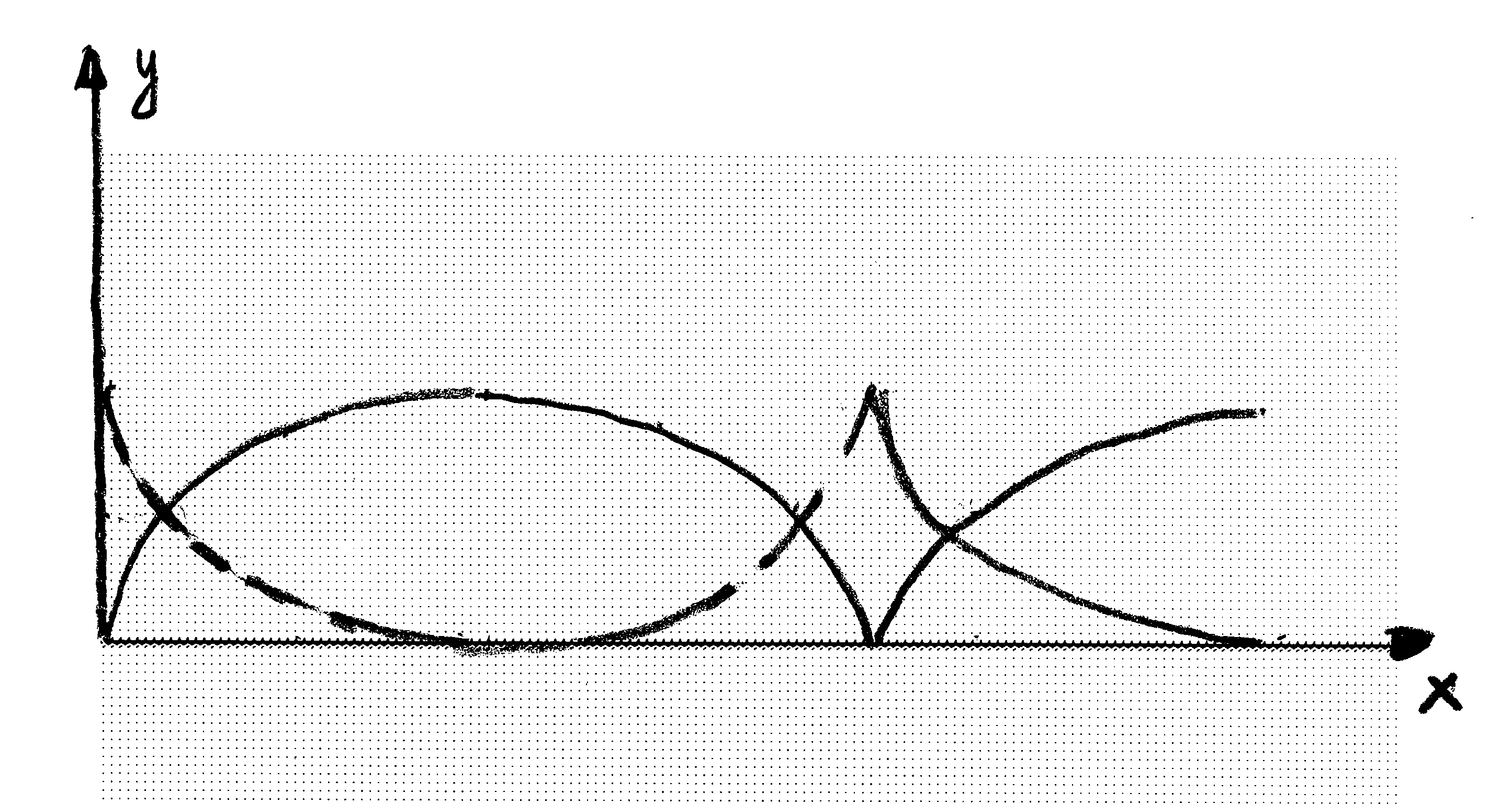
Jej wykres wygląda następująco.

Rys. 8.2.1.

Rozważmy krzywą powstającą z cykloidy (8.6) przez odbicie jej wykresu w osi poziomej i przesunięcie go o $r$ w górę. Powstaje krzywa, której wykres narysowany jest linią przerywaną na rys 8.2.1 i której opis parametryczny ma postać:

$\qquad{x=r(\alpha t-\sin\alpha t)\atop y=rcos\alpha t}$

(8.7)

Chcąc obliczyć 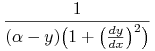$\displaystyle{\frac{1}{(\alpha-y)\big(1+\big(\frac{dy}{dx}\big)^{2}\big)}}$ dla krzywej (8.7) zauważmy, że $\dot{x}(t)>0$
i wobec tego $\displaystyle{\frac{dy}{dx}(t)=\frac{\dot{y}(t)}{\dot{x}(t)}}$

zatem

$\frac{dy}{dx}(t)=\frac{\dot{y}(t)}{\dot{x}(t)}=\frac{-r\alpha\sin\alpha t}{r\alpha-r\alpha\cos t}=\frac{-\sin\alpha t}{1-\cos\alpha t}.$

Wobec tego

$\frac{1}{\big(a-y(t)\big)\big(1+(\frac{dy}{dx})^{2}(t)\big)}=\frac{1-\cos\alpha t}{2\big(a-r\cos\alpha t\big)}$

(8.8)

Widzimy więc, że stałą wartość $\displaystyle{\frac{1}{2\alpha}}$ tego wyrażenia uzyskamy jedynie wtedy, kiedy $r=a.$ Przy tym, chcąc uzyskać $y(b)=0$ możemy przyjąć $\displaystyle{\frac{\pi}{\alpha}=b}$ tj $\displaystyle{\alpha=\frac{\pi}{b}}.$

Podsumowując: krzywa najszybszego spadku od punktu $(0,a)$ do $b,0)$ ma postać (8.7) przy $r=a$ oraz $\displaystyle{\alpha=\frac{\pi}{b}}$ i jest rozwiązaniem równania (8.5) ze stałą $\displaystyle{c=\sqrt{\frac{1}{2a}}}.$

8.2.2. Krzywa łańcuchowa

Zgodnie z rozważaniami z Wykładu 7 dla $\lambda\in\bf{R}$ szukamy punktów krytycznych funkcjonału

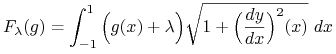$F_{\lambda}(g)=\int _{{-1}}^{{1}}\Big(g(x)+\lambda\Big)\sqrt{1+\Big(\frac{dy}{dx}\Big)^{2}(x)}\ dx$

przy warunku

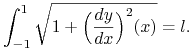$\int _{{-1}}^{{1}}\sqrt{1+\Big(\frac{dy}{dx}\Big)^{2}(x)}=l.$

(8.9)

Mamy więc funkcję Lagrange'a

$L_{\lambda}(g,\dot{g})=(g+\lambda)\sqrt{1+\dot{g}^{2}}$

i zgodnie z Twierdzeniem 8.1 otrzymujemy warunek

$E_{\lambda}\big(g,\dot{g}\big)=\big((g+\lambda\big)\big(1+\dot{g}^{2}\big)^{{1/2}}-(g+\lambda)\dot{g}^{2}\big(1+\dot{g}^{2}\big)^{{-\frac{1}{2}}}=c$

skąd

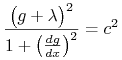$\frac{\big(g+\lambda\big)^{2}}{1+\big(\frac{dg}{dx}\big)^{2}}=c^{2}$

(8.10)

Okazuje się, że rozwiązań tego równania można poszukiwać wśród funkcji o postaci $g_{{\mu\alpha}}(x)=\mu\cosh\alpha x-\lambda.$ Istotnie, wtedy $(g_{{\mu\lambda}}+\lambda)^{2}=\mu^{2}\cosh^{2}\alpha x$ natomiast

$1+\Big(\frac{dg_{{\mu\lambda}}}{dx}\Big)^{2}=\cosh^{2}\alpha x-\sinh^{2}\alpha x+\mu^{2}\alpha^{2}\sinh^{2}\alpha x.$

Dobierając $\mu$ oraz $\alpha$ tak, aby $\mu\alpha=1$ otrzymamy (8.10) dla $c=\mu^{2}.$ Istotnie:

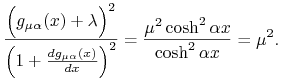$\displaystyle{\frac{\Big(g_{{\mu\alpha}}(x)+\lambda\Big)^{2}}{\Big(1+\frac{dg_{{\mu\alpha}}(x)}{dx}\Big)^{2}}=\frac{\mu^{2}\cosh^{2}\alpha x}{\cosh^{2}\alpha x}=\mu^{2}}.$

Musimy jeszcze zapewnić sobie spełnienie warunku (8.9 ), który przyjmuje postać

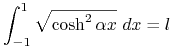$\displaystyle{\int _{{-1}}^{{1}}\sqrt{\cosh^{2}\alpha x}\ dx=l}$

czyli

$\frac{2\sinh\alpha}{\alpha}=l.$

Podsumowując.

Krzywa zwisu łańcucha o długości l zawieszonego w punktach (-1, 0) oraz (1, 0) ma postać:

$y(x)=\frac{1}{\alpha}\cosh\alpha x-\frac{1}{\alpha}\cosh\alpha,$

gdzie $\alpha$ jest rozwiązaniem równania $2\sinh\alpha-l\alpha=0.$

8.3. Równania Eulera - Lagrange'a

Niech $\mathcal{M}$ będzie układem n- punktów materialnych o przestrzeni konfiguracyjnej $\mathcal{K}$ , potencjale $\bf{U:\mathcal{K}\rightarrow R}$ i przestrzeni fazowej $\mathcal{F}.$ Niech $\gamma:{\bf R}\rightarrow\mathcal{K}$ będzie krzywą ruchu $\mathcal{M}$ taką, że $\gamma(t_{1})=x_{1}$ i $\gamma(t_{2})=x_{2}.$ Rozważmy rodzinę krzywych

$W=\{{\alpha:[t_{1},t_{2}]\rightarrow\mathcal{K}:\alpha(t_{1})=x_{1},\alpha(t_{2})=x_{2}\}}$

oraz funkcjonał $F$ na $W$ o postaci

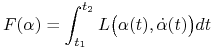$F(\alpha)=\int _{{t_{1}}}^{{t_{2}}}L\big(\alpha(t),\dot{\alpha}(t)\big)dt$

(8.11)

gdzie $L(g_{1},...,g_{n},v_{1},...,v_{n})$ jest funkcją gładką na przestrzeni $\mathcal{F}.$ Lagrange zauważył, że jeżeli funkcja $L$ ma postać

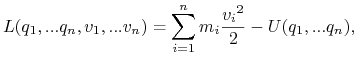$L(q_{1},...q_{n},v_{1},...v_{n})=\sum _{{i=1}}^{{n}}m_{i}\frac{{v_{i}}^{2}}{2}-U(q_{1},...q_{n}),$

(8.12)

to zagadnienie wariacyjne (8.11) ma dokładnie jedną ekstremalę, będącą krzywą ruchu $\mathcal{M}.$

Funkcję (8.12) nazywa się ”funkcją Lagrange'a” układu $\mathcal{M},$ funkcjonał (8.11) z funkcją Lagrange`a (8.12) - działaniem. Spostrzeżenie, że przyroda wybiera ekstremalę $F$ jako krzywą realizującą ruch - nazywa się zasadą najmniejszego działania.

Zweryfikujmy rachunkiem spostrzeżenie Lagrange'a. Niech $L$ ma postać 8.12. Wtedy lewe strony równań Eulera

$\frac{\partial L}{\partial q_{i}}-\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_{i}}=0$

(8.13)

mają formę:

$\displaystyle{-\frac{\partial U}{\partial q_{i}}-\frac{d}{dt}\Bigg[\frac{\partial}{\partial v_{i}}\sum _{{i=1}}^{{n}}m_{i}\frac{v_{i}^{2}}{2}\Bigg]}=-\frac{\partial U}{\partial q_{i}}-\frac{d}{dt}m_{i}v_{i}$

a zatem równania Eulera przyjmą postać równań Newtona

$\ddot{q}_{i}=-\frac{\partial U}{\partial q_{i}}$

(8.14)

Uwaga 8.1

W sformułowaniu zagadnienia wariacyjnego (8.11) jako jego istotna część występuje wybór punktów $x_{1}$ i $x_{2}.$ Na ogół jednak nie mamy pewności, że przez z góry wybrane punkty przejdzie choćby jedna krzywa ruchu naszego układu. Dlatego zagadnienie wariacyjne jest przez nas używane jedynie do wygenerowania innego opisu ekstremali za pomocą równań Eulera-Lagrange'a, który to opis nie zależy od wyboru $x_{1},x_{2}$

Uwaga 8.2

Pozornie błahe spostrzeżenie, że równanie Newtona można otrzymać jako równanie związane z zasadą wariacyjną 8.11 przy odpowiednio dobranej funkcji $L$ ma liczne i ważne konsekwencje. Oto kilka z nich.

Równania Newtona opierają się na oczywistej i dlatego niezauważalnej zasadzie, że iloraz różnicowy funkcji wektorowej jest wektorem, którego współrzędne są ilorazami różnicowymi odpowiednich współrzędnych rozważanych funkcji. Zasada ta załamuje się przy przejściu do współrzędnych krzywoliniowych. Przyjęcie jako punktu odniesienia zasady wariacyjnej pozwala otrzymać szukany ruch - ekstremalę tej zasady - posługując się dowolnymi współrzędnymi.
Idąc dalej tym tropem możemy zdefiniować krzywe ruchu jako rozwiązania układu (8.13) z odpowiednio dobraną funkcją Lagrange`a w sytuacji, kiedy bezpośrednie zastosowanie drugiej zasady mechaniki Newtona jest trudne lub niemożliwe.
Przykładem sytuacji z (2) są układy z więzami, których omówienie przeniesiemy do następnego punktu (8.4) tego wykładu.
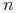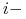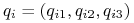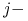Równania Eulera - Lagrange'a, dzięki swej formie, wnoszą do dyskusji o opisywanym przez nas ruchu nową informację. Jeżeli rozważamy układ $n$ cząstek, gdzie położenie $i-$ tej cząstki opisuje wektor $q_{i}=(q_{{i1}},q_{{i2}},q_{{i3}})$ oraz $j-$ ta współrzędna 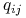$q_{{ij}}$ wektora 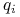$q_{i}$ nie występuje explicite w funkcji Lagrange'a (czyli potencjał U od niej nie zależy), to odpowiednie równanie 8.13 przyjmuje postać: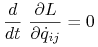

$\frac{d}{dt}\ \frac{\partial L}{\partial\dot{q}_{{ij}}}=0$ (8.15)

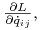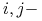Oznacza to, że wielkość $\frac{\partial L}{\partial\dot{q}_{{ij}}},$ zwana $i,j-$ tym pędem uogólnionym i oznaczana 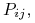$P_{{ij}},$ jest całką pierwszą ruchu.
Zauważmy, że dla funkcji Lagrange`a o postaci

$L(\gamma,\dot{\gamma})=T(\dot{\gamma})-U(\gamma)=\sum _{{i=1}}^{n}m_{i}\frac{\dot{\gamma}_{i}^{2}}{2}-U(\gamma)$ (8.16)

funkcja (8.1) przyjmuje postać

$E(\gamma,\dot{\gamma})=L(\gamma,\dot{\gamma})-\sum _{{i=1}}^{{n}}m_{i}\frac{\partial L}{\partial\dot{\gamma}_{j}}\cdot\dot{\gamma}_{j}=T(\dot{\gamma})-U(\dot{\gamma})-2T(\dot{\gamma})=-\Big(T(\dot{\gamma})+U(\gamma)\Big)$

tj całka energii (8.1) jest funkcją przeciwną do energii całkowitej. Uwaga ta daje jeszcze inny dowód prawa zachowania energii całkowitej (Twierdzenie 3.1).

8.4. Układy z więzami.

Rozważmy podrozmaitośc $M$ zanurzoną w ${\bf R}^{n}.$ Wyobraźmy sobie, że traktowany przez nas układ mechaniczny jest realizowany przez punkt $q\in{\bf R}^{n}$ a okoliczności zewnętrzne wymagają, aby w czasie ruchu pozostawał on na rozmaitości $M.$ Te okoliczności zewnętrzne nazywają sie więzami holonomicznymi.

Przykład 8.1

Kulka pozostająca wewnątrz pucharu o danym opisie analitycznym w polu ziemskiej grawitacji.
Para punktów o danych masach związana sztywno nieważkim prętem.
Ciało sztywne, czyli układ skończonej liczby punktów, których wzajemne odległości pozostają stałe.

Definicja 8.2

Niech $M$ będzie $m$ wymiarową podrozmaitością w ${\bf R}^{{3n}}$ przestrzeni konfiguracyjnej punktów $r_{1},...r_{n}$ o masach $m_{1},...,m_{n}.$ Oznaczmy przez $q=(q_{1},...q_{m})$ dowolne lokalne współrzędne na rozmaitości $M$ i niech $U(r_{1},...r_{n})$ będzie potencjałem określonym na ${\bf R}^{{3n}}.$ Ponieważ każdy punkt na rozmaitości $M$ wyznacza swoje trójki współrzędnych $(r_{1},...,r_{n})$ w ${\bf R}^{{3n}},$ to ewolucję układu z więzami można opisać za pomocą ewolucji współrzędnych $q_{1}(t),...q_{m}(t).$ Ewolucja tych współrzędnych opisana jest układem Eulera -Lagrange'a.

$\frac{\partial L}{\partial{q}_{i}}-\frac{d}{dt}\ \frac{\partial L}{\partial\dot{{q}_{i}}}=0$

(8.17)

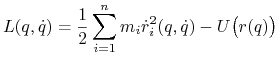$L(q,\dot{q})=\frac{1}{2}\sum _{{i=1}}^{n}m_{i}\dot{r}_{i}^{2}(q,\dot{q})-U\big(r(q)\big)$

(8.18)

a $r(q)$ jest opisem parametrycznym, wyznaczonym przez współrzędne $q.$

Uwaga 8.3

Definicja 8.2 zawiera implicite fakt, że otrzymane rozwiązanie nie zależy od od wyboru lokalnej parametryzacji (lokalnych współrzędnych) na $M.$ Istotnie, funkcję (8.18) w obszarze parametrów dla ustalonej parametryzacji otrzymamy, podstawiając $r_{i}=r_{i}(q_{1},...q_{m})$ oraz

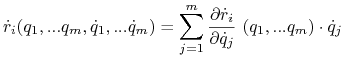$\dot{r}_{i}(q_{1},...q_{m},\dot{q}_{1},...\dot{q}_{m})=\displaystyle{\sum _{{j=1}}^{m}\frac{\partial\dot{r}_{i}}{\partial\dot{q}_{j}}\ (q_{1},...q_{m})\cdot\dot{q}_{j}}$

w funkcji Lagrange'a

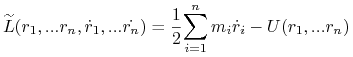$\displaystyle{\widetilde{L}(r_{1},...r_{n},\dot{r}_{1},...\dot{r_{n}})}=\frac{1}{2}\displaystyle{\sum _{{i=1}}^{n}m_{i}\dot{r}_{i}-U(r_{1},...r_{n})}$

dla ruchu pod wpływem potencjału $U$ w ${\bf R}^{{3n}}.$ Mając $L(q,\dot{q})$ jak w (8.18) i wprowadzając inne współrzędne $q$ i wyliczając podobne $L(q^{{\prime}},\dot{q^{{\prime}}})$ uzyskujemy różne przestawienia, zależne od wyboru współrzędnych dla tej samej funkcji Lagrange'a. Niezależność rozwiązań układu Eulera - Lagrange'a od wybranej parametryzacji jest konsekwencją Uwagi 8.2 (a).