Zagadnienia

11.1 Realizacja metody Broydena
11.2 Zbieżność metody Broydena

11. Metoda Broydena

W przypadku jednowymiarowym, metoda siecznych:

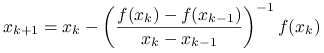$x_{{k+1}}=x_{k}-\left(\dfrac{f(x_{k})-f(x_{{k-1}})}{x_{k}-x_{{k-1}}}\right)^{{-1}}f(x_{k})$

jest interesującą alternatywą dla metody Newtona: jej zbieżność jest superliniowa (dokładniej: wykładnicza z wykładnikiem 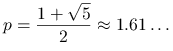$p=\dfrac{1+\sqrt{5}}{2}\approx 1.61\ldots$ — a więc tylko trochę gorsza niż metody stycznych), a za to istotny koszt jednej iteracji ogranicza się do wyznaczenia tylko jednej nowej wartości funkcji! (Pochodna jest niepotrzebna).

Uogólnienie pomysłu metody siecznych na przypadek wielowymiarowy tak, by zachować jej dwie główne cechy: superliniową zbieżność oraz niski koszt iteracji (nie wymagający w szczególności wyznaczania pochodnej ani obliczania dodatkowych wartości funkcji) nie jest trywialne i zostało zrealizowane w metodzie Broydena. Iterację Broydena określimy wzorem

$x_{{k+1}}=x_{k}-A_{k}^{{-1}}F(x_{k}),$

gdzie $A_{0}=F^{{\prime}}(x_{0})$ (lub jest jej przybliżeniem wyznaczonym za pomocą ilorazów różnicowych), a kolejne macierze $A_{k}$ wyznaczamy według wzoru

	$\displaystyle A_{{k+1}}$	$\displaystyle=A_{{k}}+\dfrac{1}{s_{k}^{T}s_{k}}F(x_{{k+1}})s_{k}^{T},$
	$\displaystyle s_{k}$	$\displaystyle=x_{{k+1}}-x_{k}.$

(Zauważmy, że $s_{k}$ jest jawnie wyznaczane w trakcie algorytmu, gdyż $s_{k}$ jest rozwiązaniem równania poprawki, $A_{k}s_{k}=-F(x_{k})$ .)

Jak widzimy z powyższej definicji, koszt jednej iteracji metody Broydena jest niewygórowany. Rzeczywiście, jeśli z poprzedniego kroku znamy rozkład LU lub QR macierzy $A_{{k-1}}$ , to wyznaczenie rozkładu $A_{{k}}$ , która jest postaci $A_{{k+1}}=A_{{k}}+u_{k}v_{k}^{T}$ , jest zadaniem wyznaczenia rozkładu dla modyfikacji macierzy rzędu 1 — a na to są znane (tanie!) algorytmy [7], [10], działające kosztem $O(N^{2})$ flopów¹⁴W metodzie Broydena nie ma więc — wbrew pozorom — potrzeby jawnego wyznaczania macierzy $A_{k}$ !, o czym szerzej mówimy w poniższym rozdziale.

11.1. Realizacja metody Broydena

Oczywiście, gdybyśmy tylko skorzystali wprost ze wzoru

$A_{{k+1}}=A_{{k}}+\dfrac{1}{s_{k}^{T}s_{k}}F(x_{{k+1}})s_{k}^{T},$

to co prawda wyznaczenie $A_{k}$ kosztowałoby nas tylko $O(N^{2})$ flopów, ale za to rozkład macierzy $A_{k}$ musiałby nas kosztować $O(N^{3})$ . Jednak, jako że macierz $A_{{k+1}}$ różni się od $A_{{k}}$ tylko o macierz rzędu jeden, będziemy mogli od razu przykładać odwrotność macierzy $A_{{k}}$ do wektora na podstawie rozkładu macierzy $A_{0}$ , kosztem jedynie $O(N^{2}+kN)$ .

Algorytm działający w oparciu o aktualizację macierzy odwrotnej do $A_{{k}}$ może być mniej stabilny numerycznie od algorytmu używającego aktualizacji rozkładu QR (zob. [10, 10.3.1, Algorytm 2]) macierzy $A_{{k}}$ i dlatego wskazuje się sposoby kontrolowania przebiegu pracy tej metody [5], którymi tutaj nie będziemy się zajmować.

Aby tanio odwracać kolejne macierze $A_{k}$ , wykorzystamy wzór Shermana–Morrisona, którego wyprowadzeniu było poświęcone ćwiczenie 5.24.

Stwierdzenie 11.1 (wzór Shermana–Morrisona)

Niech $B=A+uv^{T}$ , gdzie $A$ jest macierzą nieosobliwą $N\times N$ oraz $u,v\in\mathbb{R}^{N}$ . $B$ jest nieosobliwa wtedy i tylko wtedy, gdy $1+v^{T}A^{{-1}}u\neq 0$ i wówczas

$B^{{-1}}=\left(I-\dfrac{(A^{{-1}}u)v^{T}}{1+v^{T}A^{{-1}}u}\right)A^{{-1}}.$

U nas

$A_{{k+1}}=A_{{k}}+u_{k}v_{k}^{T},$

gdzie $u_{k}=F(x_{{k+1}})/\| s_{k}\| _{2}$ , $v_{k}=s_{k}/\| s_{k}\| _{2}$ . Oznaczając dodatkowo

$z_{k}=A_{{k}}^{{-1}}u_{k}=A_{{k}}^{{-1}}F(x_{{k+1}})/\| s_{k}\| _{2},\qquad w_{k}=\dfrac{z_{k}}{1+v_{k}^{T}z_{k}},$

ze wzoru Shermana–Morrisona mamy więc

$\displaystyle A_{{k+1}}^{{-1}}=(I-w_{k}v_{k}^{T})A_{{k}}^{{-1}}=\ldots=(I-w_{k}v_{k}^{T})\cdots(I-w_{0}v_{0}^{T})A_{{0}}^{{-1}},$

(11.1)

Wydawałoby się więc, że by skorzystać z powyższego wzoru, należałoby pamiętać dodatkowe wektory $u_{j},w_{j},v_{j}$ dla $j=0,\ldots,k$ . W rzeczywistości jednak możemy dalej wymasować powyższe zależności i wyeliminować te wektory, ograniczając się jedynie do pamiętania sekwencji poprawek $s_{0},\ldots,s_{k}$ .

Rzeczywiście, w metodzie Broydena interesuje nas przecież nie sama macierz $A_{{k+1}}^{{-1}}$ , tylko nowa wartość poprawki, $s_{{k+1}}=-A_{{k+1}}^{{-1}}F(x_{{k+1}})$ . Tymczasem, korzystając z definicji $z_{k}$ i $v_{k}$ ,

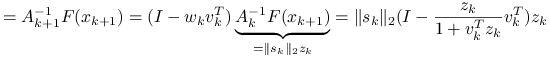	$\displaystyle-s_{{k+1}}$	$\displaystyle=A_{{k+1}}^{{-1}}F(x_{{k+1}})=(I-w_{k}v_{k}^{T})\underbrace{A_{{k}}^{{-1}}F(x_{{k+1}})}_{{=\\| s_{k}\\| _{2}z_{k}}}=\\| s_{k}\\| _{2}(I-\dfrac{z_{k}}{1+v_{k}^{T}z_{k}}v_{k}^{T})z_{k}$
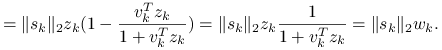		$\displaystyle=\\| s_{k}\\| _{2}z_{k}(1-\dfrac{v_{k}^{T}z_{k}}{1+v_{k}^{T}z_{k}})=\\| s_{k}\\| _{2}z_{k}\dfrac{1}{1+v_{k}^{T}z_{k}}=\\| s_{k}\\| _{2}w_{k}.$

Stąd dostajemy elegancką zależność $w_{k}=-s_{{k+1}}/\| s_{k}\| _{2}$ , którą możemy podstawić z powrotem do (11.1) i otrzymać

$\displaystyle-s_{{k+1}}=A_{{k+1}}^{{-1}}F(x_{{k+1}})=\left(I+\dfrac{s_{{k+1}}s_{k}^{T}}{\| s_{k}\| _{2}^{2}}\right)A_{k}^{{-1}}F(x_{{k+1}}).$

(11.2)

Na tej podstawie ( $s_{{k+1}}$ występuje po obu stronach tej równości!) konkludujemy, że

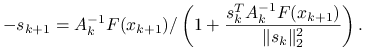$\displaystyle-s_{{k+1}}=A_{k}^{{-1}}F(x_{{k+1}})/\left(1+\frac{s_{k}^{T}A_{k}^{{-1}}F(x_{{k+1}})}{\| s_{k}\| _{2}^{2}}\right).$

(11.3)

Ćwiczenie 11.1

Wykaż, że jeśli $A_{{k+1}}$ jest nieosobliwa, to wyrażenie pojawiające się w mianowniku wzoru na $s_{{k+1}}$ jest różne od zera.

Wskazówka:

Zauważ, że $\frac{s_{k}^{T}A_{k}^{{-1}}F(x_{{k+1}})}{\| s_{k}\| _{2}^{2}}=v_{k}^{T}A_{k}^{{-1}}u_{k}$ i skorzystaj ze wzoru Shermana–Morrisona.

Ćwiczenie 11.2

Zaimplementuj metodę Broydena z zastosowaniem wzoru Shermana–Morrisona.

Rozwiązanie:

Aby sensownie wyznaczać $s_{{k+1}}$ , musimy zastanowić się chwilę, jak wyznaczać wektor

$p_{k}=A_{k}^{{-1}}F(x_{{k+1}}),$

występujący we wzorze (11.3). Zauważmy, że na mocy (11.1),

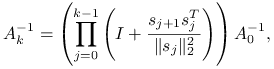$A_{k}^{{-1}}=\left(\prod _{{j=0}}^{{k-1}}\left(I+\dfrac{s_{{j+1}}s_{{j}}^{T}}{\| s_{{j}}\| _{2}^{2}}\right)\right)A_{0}^{{-1}},$

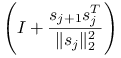a więc wyznaczenie $p_{k}$ daje się zrealizować w pętli polegającej na kolejnym mnożeniu przez macierze postaci $\left(I+\dfrac{s_{{j+1}}s_{{j}}^{T}}{\| s_{{j}}\| _{2}^{2}}\right)$ . Pamiętajmy, by macierzy postaci $I+uv^{T}$ nigdy nie formować explicite, a w zamian wyznaczać iloczyn $(I+uv^{T})p$ zgodnie z wzorem

$p+u(v^{T}p),$

co będzie kosztowało tylko $O(N)$ flopów. Szkielet algorytmu mógłby więc wyglądać następująco:

Bazowa implementacja metody Broydena

$x=x_{0}$ ; k = 0;

$A_{0}=F^{{\prime}}(x)$ ;

wyznacz rozkład LU lub QR macierzy $A_{0}$ ;

rozwiąż, korzystając z gotowego rozkładu, $A_{0}s_{0}=-F(x)$ ;

while not stop do

begin

$x=x+s$ ;

oblicz $F(x)$ ;

k = k+1;

rozwiąż, korzystając z gotowego rozkładu, $A_{0}s=-F(x)$ ;

for j = 0 to k-1

begin

$s=s+s_{{j+1}}(s_{{j}}^{T}s)/\| s_{{j}}\| _{2}^{2}$ ;

end

$s=s/(1+s_{{k-1}}^{T}s/\| s_{{k-1}}\| _{2}^{2})$ ;

$s_{k}=s$ ;

end

Jak widać, musimy pamiętać czynniki rozkładu $A_{0}$ (samego $A_{0}$ już nie) oraz wszystkie pośrednie poprawki $s_{0},s_{1},\ldots$ .

11.2. Zbieżność metody Broydena

Poniższe twierdzenie gwarantuje superliniową zbieżność metody Broydena nawet w przypadku, gdy $A_{0}\approx F^{{\prime}}(x_{0})$ .

Twierdzenie 11.1 (o zbieżności metody Broydena)

Przy standardowych założeniach, istnieją $\delta$ oraz $\delta _{0}$ (dostatecznie małe) takie, że jeśli $x_{0}\in K(x^{*},\delta)$ oraz $\| A_{0}-F^{{\prime}}(x^{*})\|<\delta _{0}$ , to metoda Broydena startująca z $x_{0}$ i $A_{0}$ jest dobrze określona oraz $x_{k}\rightarrow x^{*}$ superliniowo.

Dowód

Zobacz np. [9].

∎

Ćwiczenie 11.3

Wykaż, że jeśli $A_{0}=F^{{\prime}}(x_{0})$ oraz $x_{0}$ jest dostatecznie blisko $x^{*}$ , to powyższe twierdzenie zachodzi.

Rozwiązanie:

To oczywiste, gdyż

$\| A_{0}-F^{{\prime}}(x^{*})\|=\| F^{{\prime}}(x_{0})-F^{{\prime}}(x^{*})\|\leq L\| x_{0}-x^{*}\|\leq L\delta.$

Biorąc $\delta$ , $\delta _{0}$ z twierdzenia o zbieżności metody Broydena i ewentualnie dodatkowo zmniejszając $\delta$ tak, by jednocześnie $L\delta<\delta _{0}$ , dostajemy

$\| A_{0}-F^{{\prime}}(x^{*})\|\leq L\delta<\delta _{0},$

co gwarantuje spełnienie wszystkich założeń twierdzenia 11.1.

Ćwiczenie 11.5

Wykaż, że macierze $A_{k}$ generowane w metodzie Broydena spełniają równanie siecznych,

$A_{{k+1}}(x_{{k+1}}-x_{{k}})=F(x_{{k+1}})-F(x_{{k}}).$

Rozwiązanie:

Z definicji

$A_{{k+1}}=A_{{k}}+\dfrac{1}{s_{k}^{T}s_{k}}F(x_{{k+1}})s_{k}^{T},$

więc mnożąc przez $x_{{k+1}}-x_{{k}}=s_{k}$ mamy

$A_{{k+1}}s_{k}=A_{{k}}s_{k}+F(x_{{k+1}})=-F(x_{{k}})+F(x_{{k+1}}).$

Ćwiczenie 11.6

Niech $A\in\mathbb{R}^{{N\times N}}$ oraz $s,y\in\mathbb{R}^{N}$ przy czym $s\neq 0$ . Wtedy

$\min _{{B\in\mathbb{R}^{{N\times N}}:\; Bs=y}}\| A-B\| _{2}$

jest osiągane dla

$B^{*}=A+\dfrac{(y-As)s^{T}}{s^{T}s}.$

Znaczy to, że metoda Broydena generuje ciąg macierzy $A_{k}$ taki, że $A_{{k+1}}$ jest najbliższe $A_{k}$ w normie spektralnej wśród wszystkich macierzy spełniających równanie siecznych

$A_{k}(x_{{k}}-x_{{k-1}})=F(x_{{k}})-F(x_{{k-1}}).$

Rozwiązanie:

Wystarczy pokazać, że dla dowolnej innej macierzy $B$ spełniającej $Bs=y$ , norma różnicy $B-A$ nie jest mniejsza niż dla $B^{*}-A$ . Mamy

$B^{*}-A=\dfrac{(y-As)s^{T}}{s^{T}s}=\dfrac{(Bs-As)s^{T}}{s^{T}s}=\dfrac{(B-A)ss^{T}}{s^{T}s},$

skąd

$\| B^{*}-A\| _{2}\leq\| B-A\| _{2}\| ss^{T}\|/\| s\| _{2}^{2}=\| B-A\| _{2}.$

Ostatnia równość wynika z faktu, że $\| xy^{T}\| _{2}=\| x\| _{2}\,\| y\| _{2}$ .

Na zakończenie wspomnijmy, że — podobnie jak w przypadku modyfikacji metody Newtona — rozsądne jest wykonać co pewną liczbę iteracji restart metody Broydena, to znaczy: uruchomić procedurę na nowo, biorąc za punkt początkowy ostatnio wyznaczone przybliżenie. W ten sposóby spowodujemy aktualizację macierzy pochodnej (tej z ,,zerowego” kroku) oraz zmniejszymy liczbę czynników iloczynu macierzy rzędu jeden koniecznych do obliczenia poprawki.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Matematyka obliczeniowa II

Zagadnienia

11. Metoda Broydena

11.1. Realizacja metody Broydena

Stwierdzenie 11.1 (wzór Shermana–Morrisona)

Ćwiczenie 11.1

Ćwiczenie 11.2

Bazowa implementacja metody Broydena

11.2. Zbieżność metody Broydena

Twierdzenie 11.1 (o zbieżności metody Broydena)

Dowód

Ćwiczenie 11.3

Ćwiczenie 11.5

Ćwiczenie 11.6