Zagadnienia
14. Metody Monte Carlo
14.1. Wstęp, metody niedeterministyczne
Poprzedni wykład zakończyliśmy pesymistycznym twierdzeniem 13.4, że nie istnieją efektywne metody numerycznego całkowania funkcji wielu zmiennych, ponieważ ma miejsce zjawisko przekleństwa wymiaru. Zwróćmy jednak uwagę na to, że fakt istnienia przekleństwa wymiaru stwierdziliśmy przy założeniach, że:
(i) model obliczeniowy jest deterministyczny,
(ii) funkcje podcałkowe są
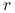 -krotnie
różniczkowalne po każdej zmiennej.
-krotnie
różniczkowalne po każdej zmiennej.
Można mieć nadzieję, że przekleństwo wymiaru zniknie, albo zostanie złagodzone, gdy przynajmniej jedno z tych założeń nie będzie spełnione.
Ten wykład poświęcimy (klasycznej) metodzie Monte Carlo numerycznego całkowania, która jest przykładem metody niedeterministycznej, tzn. takiej, która oblicza wynik wykorzystując zjawiska losowe. Chociaż może to brzmieć dziwnie, to właśnie niedeterministyczne zachowanie metody pozwala pokonać przekleństwo wymiaru.
Opisana dalej klasyczna metoda Monte Carlo związana jest ściśle ze Stanisławem Ulamem, uczniem Stefana Banacha i reprezentantem Lwowskiej Szkoły Matematycznej. Ulam zastosował metodę Monte Carlo do obliczania skomplikowanych całek w ramach ,,Manhattan Project” w Los Alamos (USA), w czasie II Wojny światowej.
14.2. Klasyczna metoda Monte Carlo
14.2.1. Definicja i błąd
Tak jak w poprzednim rozdziale chcemy obliczyć całkę
![I_{d}(f)\,:=\,\int _{{[0,1]^{d}}}f(\vec{x})\, d\vec{x}\,=\,\underbrace{\int _{0}^{1}\int _{0}^{1}\cdots\int _{0}^{1}}_{d}f(x_{1},x_{2},\ldots,x_{d})\, dx_{1}dx_{2}\cdots dx_{d}.](wyklady/mo2/mi/mi2522.png) |
Zakładamy przy tym, że ![]() jest funkcją,
której kwadrat jest całkowalny,
jest funkcją,
której kwadrat jest całkowalny,
Definicja 14.1
Klasyczna metoda Monte Carlo polega na przybliżeniu
![]() średnią arytmetyczną wartości funkcji
średnią arytmetyczną wartości funkcji ![]() w losowo wybranych punktach, tzn.
w losowo wybranych punktach, tzn.
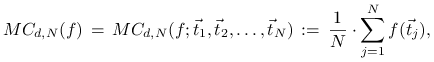 |
gdzie ![]() są punktami wylosowanymi
niezależnie od siebie, każdy zgodnie z rozkładem jednostajnym na
są punktami wylosowanymi
niezależnie od siebie, każdy zgodnie z rozkładem jednostajnym na
![]() .
.
Konsekwencją zastosowania losowości jest to, że przy różnych
realizacjach metody otrzymujemy różne wyniki, w zależności
od wyboru punktów ![]() . Wynik
. Wynik ![]() jest więc
zmienną losową, której wartość oczekiwana wynosi
jest więc
zmienną losową, której wartość oczekiwana wynosi
![\displaystyle\frac{1}{N}\sum _{{j=1}}^{N}\int _{{[0,1]^{d}}}f(\vec{t})\, d\vec{t}\,=\, I_{d}(f).](wyklady/mo2/mi/mi2418.png) |
Ponieważ różnica ![]() jest też zmienną losową,
za błąd metody Monte Carlo dla danej funkcji
jest też zmienną losową,
za błąd metody Monte Carlo dla danej funkcji ![]() przyjmiemy
odchylenie standardowe,
przyjmiemy
odchylenie standardowe,
Twierdzenie 14.1
Dla danej funkcji ![]() błąd metody Monte Carlo wynosi
błąd metody Monte Carlo wynosi
gdzie
jest wariancją funkcji ![]() .
.
Zanim przystąpimy do dowodu zauważmy, że ![]() jest dobrze
zdefiniowaną wielkością, bowiem nierówność
jest dobrze
zdefiniowaną wielkością, bowiem nierówność
jest szczególnym przypadkiem znanej nierówności Schwarza dla całek.
Dowód
Oznaczmy, dla uproszczenia, zmienną losową ![]() . Wtedy
. Wtedy
| (14.1) |
Ponadto
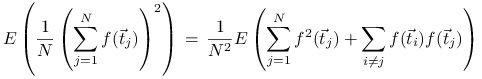 |
||||
gdzie skorzystaliśmy z niezależności zmiennych losowych ![]() i
i ![]() dla
dla ![]() . Stąd i z (14.1) dostajemy
. Stąd i z (14.1) dostajemy
co kończy dowód.
∎Uwaga 14.1
Zauważmy, że w dowodzie pokazaliśmy przy okazji nierówność Schwarza posługując się narzędziami rachunku prawdopodobieństwa.
Twierdzenie (14.1) mówi, że błąd metody Monte Carlo jest
proporcjonalny do ![]() przy bardzo słabych wstępnych założeniach
na funkcję (jedynie całkowalność kwadratu funkcji). Jest to istotna
poprawa w porównaniu do błędu
przy bardzo słabych wstępnych założeniach
na funkcję (jedynie całkowalność kwadratu funkcji). Jest to istotna
poprawa w porównaniu do błędu ![]() dla metod deterministycznych.
W szczególności ważne jest, że wykładnik
dla metod deterministycznych.
W szczególności ważne jest, że wykładnik ![]() przy
przy ![]() jest niezależny od wymiaru
jest niezależny od wymiaru ![]() , a konsekwencją tego
pokonanie przekleństwa wymiaru.
, a konsekwencją tego
pokonanie przekleństwa wymiaru.
Dziwnym może wydawać się, że przekleństwo wymiaru można
zlikwidować używając metod niedeterministycznych (losowych).
Jednak niczego nie ma za darmo. Należy pamiętać, że jest to
możliwe za cenę niepewności wyniku. O ile bowiem metoda
deterministyczna produkuje zawsze ten sam wynik, metoda
niedeterministyczna (taka jak Monte Carlo) produkuje różne
wyniki zależnie od konkretnych realizacji zmiennych losowych.
Dlatego, mimo iż błąd oczekiwany jest proporcjonalny do ![]() to nie mamy całkowitej pewności, że przy konkretnej realizacji
otrzymany wynik jest tego samego rzędu. Z tego punktu widzenia warto
przytoczyć następującą równość, która wynika
z centralnego twierdzenia granicznego; mianowicie, dla
dowolnych
to nie mamy całkowitej pewności, że przy konkretnej realizacji
otrzymany wynik jest tego samego rzędu. Z tego punktu widzenia warto
przytoczyć następującą równość, która wynika
z centralnego twierdzenia granicznego; mianowicie, dla
dowolnych ![]() mamy
mamy
gdzie Prob oznacza prawdopodobieństwo względem
rozkładu jednostajnego na ![]() .
.
14.2.2. Całkowanie z wagą
Deterministyczne metody interpolacyjne z poprzedniego rozdziału można
stosować jedynie do całkowania na ![]() -wymiarowych prostokątach.
Metoda Monte Carlo ma oprócz wymienionych również i tą zaletę, że
łatwo ją uogólnić na przypadek całkowania z wagą. Dla przybliżenia
wartości
-wymiarowych prostokątach.
Metoda Monte Carlo ma oprócz wymienionych również i tą zaletę, że
łatwo ją uogólnić na przypadek całkowania z wagą. Dla przybliżenia
wartości
możemy bowiem zastosować wzór
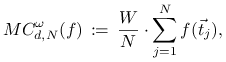 |
przy czym ![]() są tym razem punktami wybranymi
losowo i niezależnie od siebie, zgodnie z rozkładem na
są tym razem punktami wybranymi
losowo i niezależnie od siebie, zgodnie z rozkładem na ![]() o gęstości
o gęstości ![]() .
.
Adaptując odpowiednio dowód twierdzenia 14.1 otrzymujemy następujące wyrażenie na błąd uogólnionej metody Monte Carlo.
Twierdzenie 14.2
Niech
![]() .
Wtedy
.
Wtedy
gdzie
14.3. Redukcja wariancji
Zauważyliśmy, że zaletą metody Monte Carlo jest nie tylko jej
prostota, ale również to, że błąd średni wynosi ![]() .
Naturalnym jest teraz pytanie, czy błędu tego nie można poprawić.
Temu celowi służą metody redukcji wariancji, które polegają
w ogólności na redukcji czynnika
.
Naturalnym jest teraz pytanie, czy błędu tego nie można poprawić.
Temu celowi służą metody redukcji wariancji, które polegają
w ogólności na redukcji czynnika ![]() . Spośród wielu technik
redukcji wariancji skupimy uwagę na dwóch: losowaniu warstwowemu oraz
funkcjach kontrolnych. Dla uproszczenia będziemy zakładać, że
całkujemy z wagą jednostkową na kostce
. Spośród wielu technik
redukcji wariancji skupimy uwagę na dwóch: losowaniu warstwowemu oraz
funkcjach kontrolnych. Dla uproszczenia będziemy zakładać, że
całkujemy z wagą jednostkową na kostce
14.3.1. Losowanie warstwowe
Podzielmy obszar całkowania ![]() na
na ![]() rozłącznych podzbiorów
rozłącznych podzbiorów ![]() tak, że
tak, że
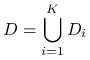 |
i zastosujmy Monte Carlo do całkowania po każdym ![]() , tzn. całkę
, tzn. całkę
![]() przybliżymy wielkością
przybliżymy wielkością
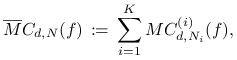 |
gdzie ![]() jest metodą Monte Carlo zastosowaną do całki
jest metodą Monte Carlo zastosowaną do całki
oraz ![]() .
.
Oznaczmy przez ![]() objętość
objętość ![]() -wymiarową podzbioru
-wymiarową podzbioru ![]() .
Ponieważ zmienne losowe
.
Ponieważ zmienne losowe ![]() są parami
niezależne dla
są parami
niezależne dla ![]() , na podstawie twierdzenia 14.2 mamy
, na podstawie twierdzenia 14.2 mamy
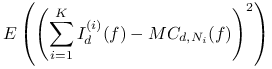 |
||||
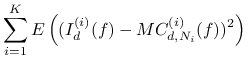 |
||||
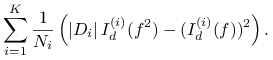 |
Przyjmijmy teraz, że
przy czym dla uproszczenia (ale bez utraty ogólności) zakładamy, że wielkości te są całkowite. Wtedy otrzymujemy
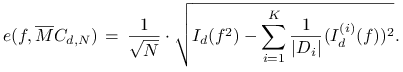 |
(14.2) |
Błąd tak zdefiniowanej metody
![]() nie jest większy od błędu klasycznej
metody
nie jest większy od błędu klasycznej
metody ![]() z Twierdzenia 14.1.
z Twierdzenia 14.1.
Twierdzenie 14.3
Dla dowolnej funkcji ![]() takiej, że
takiej, że ![]() mamy
mamy
przy czym równość zachodzi tylko wtedy gdy iloraz
![]() jest stały, niezależnie od
jest stały, niezależnie od ![]() .
.
Dowód
Rzeczywiście, oznaczając
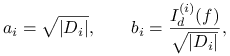 |
oraz wykorzystując nierówność Schwarza dla ciągów mamy
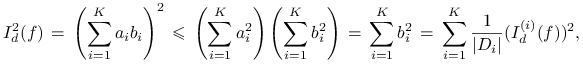 |
przy czym równość zachodzi tylko wtedy gdy wektory
![]() i
i ![]() są liniowo zależne,
co jest równoważne warunkowi w treści twierdzenia.
są liniowo zależne,
co jest równoważne warunkowi w treści twierdzenia.
Prawdziwość tezy pokazuje teraz porównanie wzorów na błędy obu metod.
∎Widzimy, że stosując losowanie warstwowe z ustalonym podziałem
na ![]() podzbiory
podzbiory ![]() możemy co prawda zmiejszyć błąd, ale szybkość
zbieżności
możemy co prawda zmiejszyć błąd, ale szybkość
zbieżności ![]() pozostaje ta sama. A czy można poprawić
zbieżność stosując różne podziały dla różnych wartości
pozostaje ta sama. A czy można poprawić
zbieżność stosując różne podziały dla różnych wartości ![]() ?
Okazuje się, że tak, o ile założymy pewną regularność funkcji
?
Okazuje się, że tak, o ile założymy pewną regularność funkcji ![]() .
.
Aby to uzyskać, najpierw przekształcimy wzór (14.2)
na błąd metody ![]() do postaci
do postaci
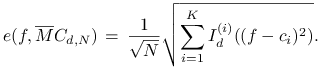 |
(14.3) |
gdzie
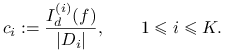 |
Załóżmy teraz, że ![]() spełnia warunek Lipschitza ze stałą
spełnia warunek Lipschitza ze stałą ![]() ,
,
Wtedy istnieją ![]() takie, że
takie, że ![]() ,
a stąd i z lipschitzowskości
,
a stąd i z lipschitzowskości ![]() mamy, że dla dowolnego
mamy, że dla dowolnego ![]()
gdzie
jest średnicą zbioru ![]() w normie max. W konsekwencji, ze wzoru
(14.3) dostajemy następujące oszacowanie błędu:
w normie max. W konsekwencji, ze wzoru
(14.3) dostajemy następujące oszacowanie błędu:
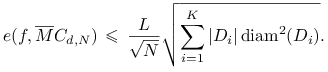 |
Ustalmy teraz równomierny podział kostki ![]() na
na ![]() podkostek
podkostek ![]() ,
każda o krawędzi długości
,
każda o krawędzi długości ![]() (zakładamy, bez zmniejszenia
ogólności, że
(zakładamy, bez zmniejszenia
ogólności, że ![]() jest całkowita) tak, że nasza metoda
aproksymuje całkę na
jest całkowita) tak, że nasza metoda
aproksymuje całkę na ![]() używając tylko jednej wartości. Wtedy
używając tylko jednej wartości. Wtedy
![]() oraz
oraz
Ostatecznie, otrzymany w ten sposób wariant losowania warstwowego jest
zbieżny z wykładnikiem większym niż ![]() . Oczywiście, może to mieć
praktyczne znaczenie jedynie dla małych wymiarów
. Oczywiście, może to mieć
praktyczne znaczenie jedynie dla małych wymiarów ![]() , bowiem dla
dużych
, bowiem dla
dużych ![]() wykładnik
wykładnik ![]() jest właściwie równy
jest właściwie równy ![]() .
.
14.3.2. Funkcje kontrolne
Podobny efekt zwiększenia szybkości zbieżności można uzyskać
stosując klasyczną Monte Carlo bezpośrednio do funkcji ![]() ,
gdzie
,
gdzie ![]() jest pewną specjalnie dobraną funkcją, zwaną
funkcją kontrolną.
jest pewną specjalnie dobraną funkcją, zwaną
funkcją kontrolną.
Rzeczywiście, przedstawmy ![]() w postaci
w postaci ![]() . Wtedy
. Wtedy
co sugeruje zastosowanie następującej metody:
Pozostaje kwestia doboru funkcji ![]() tak, aby istotnie zmniejszyć
wariancję
tak, aby istotnie zmniejszyć
wariancję ![]() . Weźmy najpierw funkcję schodkową postaci
. Weźmy najpierw funkcję schodkową postaci
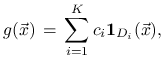 |
gdzie
jest funkcją charakterystyczną zbioru ![]() , a
, a ![]() dla dowolnych
dla dowolnych ![]() . Oczywiście, najlepiej byłoby
wziąć
. Oczywiście, najlepiej byłoby
wziąć ![]() tak, aby
tak, aby ![]() , ale jest to
niemożliwe, bo nie znamy całek
, ale jest to
niemożliwe, bo nie znamy całek ![]() . (Znajomość tych
całek nie była konieczna w przypadku losowania warstwowego!) Wtedy
dostajemy ten sam efekt jak dla
. (Znajomość tych
całek nie była konieczna w przypadku losowania warstwowego!) Wtedy
dostajemy ten sam efekt jak dla ![]() , tzn. dla
lipschitzowskiej
, tzn. dla
lipschitzowskiej ![]()
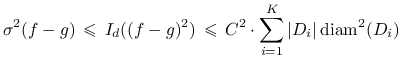 |
(14.4) |
i dla ![]() odpowiadającej równomiernemu podziałowi na
odpowiadającej równomiernemu podziałowi na ![]() podkostek
otrzymujemy błąd proporcjonalny do
podkostek
otrzymujemy błąd proporcjonalny do ![]() .
.
W ogólności, funkcję ![]() należy w praktyce wybierać tak, aby
dobrze aproksymowała funkcję
należy w praktyce wybierać tak, aby
dobrze aproksymowała funkcję ![]() . Oczywiście, wybór ten musi
bazować na informacji jaką posiadamy o
. Oczywiście, wybór ten musi
bazować na informacji jaką posiadamy o ![]() .
.
Na przykład, dla funkcji ![]() -gładkich, tzn. dla
-gładkich, tzn. dla ![]() można w ten sposób dostać jeszcze lepszy wykładnik. Rzeczywiście,
niech
można w ten sposób dostać jeszcze lepszy wykładnik. Rzeczywiście,
niech ![]() będzie kawałkami wielomianem stopnia najwyżej
będzie kawałkami wielomianem stopnia najwyżej ![]() po każdej zmiennej interpolującym
po każdej zmiennej interpolującym ![]() , dla równomiernego podziału
kostki jednostkowej na
, dla równomiernego podziału
kostki jednostkowej na ![]() podkostek. Z rozdziału 13 wiemy,
że wtedy dla funkcji
podkostek. Z rozdziału 13 wiemy,
że wtedy dla funkcji ![]() błąd interpolacji jest
postaci (zob. twierdzenie 13.2)
błąd interpolacji jest
postaci (zob. twierdzenie 13.2)
W konsekwencji, dla tak skonstruowanej metody dostajemy następujący błąd oczekiwany.
Twierdzenie 14.4
Dla ![]() mamy
mamy
Dodajmy, że ![]() jest w istocie metodą mieszaną,
gdyż używa wartości funkcji
jest w istocie metodą mieszaną,
gdyż używa wartości funkcji ![]() obliczanych w
obliczanych w ![]() punktach
wybranych deterministycznie oraz w
punktach
wybranych deterministycznie oraz w ![]() punktach wybranych losowo.
punktach wybranych losowo.
Zbieżności ![]() nie da się już poprawić w klasie
nie da się już poprawić w klasie
![]() . Dokładniej, można pokazać następujące twierdzenie,
które jest odpowiednikiem twierdzenia 13.4 dla algorytmów
niedeterministycznych.
. Dokładniej, można pokazać następujące twierdzenie,
które jest odpowiednikiem twierdzenia 13.4 dla algorytmów
niedeterministycznych.
Twierdzenie 14.5
Istnieje ![]() o następującej własności: dla dowolnej (deterministycznej
lub niedeterministycznej) aproksymacji całki wykorzystującej
o następującej własności: dla dowolnej (deterministycznej
lub niedeterministycznej) aproksymacji całki wykorzystującej ![]() wartości
funkcji istnieje
wartości
funkcji istnieje ![]() dla której
dla której ![]() ,
a błąd oczekiwany aproksymacji całki wynosi co najmniej
,
a błąd oczekiwany aproksymacji całki wynosi co najmniej ![]() .
.
14.4. Generowanie liczb (pseudo-)losowych
Dotychczas milcząco przyjmowaliśmy, że umiemy generować ciągi
niezależnych liczb losowych zgodnie z danym rozkładem prawdopodobieństwa.
Nie jest to jednak zadanie trywialne. W praktyce obliczeniowej liczby
losowe uzyskujemy przez zastosowanie specjalnych programów. Ponieważ
komputer jest urządzeniem deterministycznym, tak uzyskane ciągi nie są
idealnie losowe już choćby dlatego, że są okresowe. Fakt ten wpływa
na pogorszenie jakości wyniku i w szczególności powoduje, że ich
użycie pozwala uzyskać jedynie kilka liczb znaczących, przy czym
im większy wymiar ![]() zadania tym gorsza graniczna dokładność.
Z tych względów mówimy raczej o generatorach liczb pseudo-losowych.
zadania tym gorsza graniczna dokładność.
Z tych względów mówimy raczej o generatorach liczb pseudo-losowych.
Generowanie liczb pseudolosowych jest bardzo obszernym tematem, my tylko zwrócimy uwagę na podstawowe metody.
14.4.1. Liniowy generator kongruencyjny
Liniowe generatory kongruencyjne służą generowaniu ciągów
losowych ![]() o rozkładzie jednostajnym na odcinku
o rozkładzie jednostajnym na odcinku ![]() i
zdefiniowane są w następujący prosty sposób. Startujemy z
i
zdefiniowane są w następujący prosty sposób. Startujemy z ![]() i kolejno obliczamy dla
i kolejno obliczamy dla ![]()
Jakość takiego generatora zależy istotnie o wyboru liczb całkowitych
![]() ,
, ![]() i
i ![]() . W szczgólności pożądane jest, aby generator miał
maksymalny okres
. W szczgólności pożądane jest, aby generator miał
maksymalny okres ![]() . Jeśli
. Jeśli ![]() to warunkami dostatecznymi na to są:
to warunkami dostatecznymi na to są:
(a)
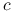 i
i 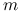 są względnie pierwsze,
są względnie pierwsze,(b) jeśli
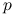 dzieli
dzieli 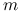 to
to 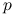 dzieli
dzieli  ,
,(c) jeśli
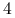 dzieli
dzieli 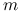 to
to 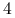 dzieli
dzieli  .
.
Dostęp do dobrego generatora liczb losowych o rozkładnie jednostajnym
![]() jest ważny również z tego względu, że
jest on zwykle podstawą dla konstrukcji generatorów ciągów o bardziej
skomplikowanych rozkładach prawdopodobieństwa.
jest ważny również z tego względu, że
jest on zwykle podstawą dla konstrukcji generatorów ciągów o bardziej
skomplikowanych rozkładach prawdopodobieństwa.
14.4.2. Odwracanie dystrybuanty i ,,akceptuj albo odrzuć”
Jeśli znana jest dystrybuanta żądanego rozkładu, czyli funkcja
oraz łatwo obliczyć jej odwrotność zdefiniowaną jako
to potrzebne ciągi losowe mogą być wygenerowane według wzoru
Rzeczywiście, mamy
Na przykład, jeśli ![]() to można zastosować wzór
to można zastosować wzór
![]() .
.
Niestety, dla wielu rozkładów dystrybuanta nie może być
dokładnie obliczona. Wtedy jakość metody zależy od jakości
zastosowanej numerycznej aproksymacji funkcji ![]() .
.
Inna uniwersalna metoda generowania liczb losowych o dowolnym
rozkładzie na ![]() , zwana akceptuj albo odrzuć, polega na
wykorzystaniu istniejącego ,,dobrego” generatora liczb innego
rozkładu na
, zwana akceptuj albo odrzuć, polega na
wykorzystaniu istniejącego ,,dobrego” generatora liczb innego
rozkładu na ![]() . Dokładniej, załóżmy, że dysponujemy
generatorem liczb losowych
. Dokładniej, załóżmy, że dysponujemy
generatorem liczb losowych ![]() zgodnie z rozkładem o gęstości
zgodnie z rozkładem o gęstości
![]() , a interesują nas liczby
, a interesują nas liczby ![]() pochodzące z rozkładu
o gęstości
pochodzące z rozkładu
o gęstości ![]() . Załóżmy ponadto, że
. Załóżmy ponadto, że
dla pewnej stałej ![]() . Wtedy możemy użyć następującego
algorytmu:
. Wtedy możemy użyć następującego
algorytmu:
|
|
repeat | |
| . | . | generuj |
| . | . | generuj |
| . | until |
|
| . | return |
|
Aby pokazać poprawność takiego generatora zauważmy, że
Ponieważ dla ![]() prawdopodobieństwo, że
prawdopodobieństwo, że ![]() wynosi
wynosi ![]() to
to
i w konsekwencji dostajemy
14.4.3. Metoda Box-Muller dla rozkładu gaussowskiego
Normalny rozkład gaussowski na ![]() o funkcji gęstości
o funkcji gęstości
jest najczęściej stosowanym rozkładem niejednostajnym.
Dla rozkładu gaussowskiego bardzo efektywne okazują się algorytmy
bazujące na odwracaniu dystrybuanty. Używają one dość
skomplikowanych aproksymacji funkcji ![]() .
.
Prostszą i najbardziej popularną jest metoda Box-Muller.
Generuje ona od razu dwie niezależne liczby ![]() i
i ![]() (albo,
równoważnie, punkt
(albo,
równoważnie, punkt ![]() zgodnie z rozkładem
normalnym w
zgodnie z rozkładem
normalnym w ![]() ), na podstawie dwóch liczb losowych o rozkładzie
jednostajnym.
), na podstawie dwóch liczb losowych o rozkładzie
jednostajnym.
Przedstawmy ![]() we współrzędnych biegunowych,
we współrzędnych biegunowych,
gdzie ![]() i
i ![]() . Metoda polega
na wygenerowaniu zmiennych
. Metoda polega
na wygenerowaniu zmiennych ![]() i
i ![]() , a następnie zastosowaniu
powyższego wzoru. Generowanie
, a następnie zastosowaniu
powyższego wzoru. Generowanie ![]() jest proste, bo ma rozkład
jednostajny. Policzmy dystrybuantę rokładu zmiennej
jest proste, bo ma rozkład
jednostajny. Policzmy dystrybuantę rokładu zmiennej ![]() . Mamy
. Mamy
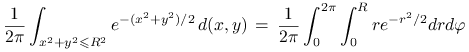 |
||||
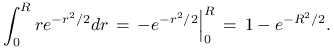 |
Stąd, stosując metodę odwracania dystrybuanty mamy
![]() ,
, ![]() .
Rachunki te prowadzą do następującego generatora.
.
Rachunki te prowadzą do następującego generatora.
|
|
generuj |
| . |
|
| . |
|
| . | return |




