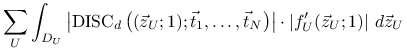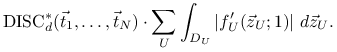Zagadnienia
15. Metody quasi-Monte Carlo
15.1. Co to są metody quasi-Monte Carlo?
Metody Monte Carlo potrafią pokonać przekleństwo wymiaru, mają jednak również swoje wady. Najważniejsze z nich to:
(i) niepewność wyniku (który ma charakter probablistyczny),
(ii) stosunkowo wolna zbieżność (praktycznie
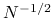 ),
),(iii) konieczność stosowania (niekiedy skomplikowanych) generatorów liczb losowych.
Można powiedzieć, że skoro używamy z powodzeniem generatorów
liczb pseudo-losowych, to implementacje Monte Carlo są w istocie
deterministyczne. Dlatego, wybierając punkty deterministycznie, ale
tak, aby w jakiś sposób ,,udawały” i ,,uśredniały” wybór losowy,
powinniśmy dostać metodę deterministyczną o zbieżności co
najmniej ![]() . A przy okazji usunęlibyśmy dwie
z wymienionych wad Monte Carlo.
. A przy okazji usunęlibyśmy dwie
z wymienionych wad Monte Carlo.
Takie intuicyjne myślenie wydaje się nie mieć racjonalnych
podstaw, bo przecież metody deterministyczne podlegają
przekleństwu wymiaru. Pamiętajmy jednak, że twierdzenie 13.4
o przekleństwie zachodzi w klasie ![]() funkcji
różniczkowalnych
funkcji
różniczkowalnych ![]() razy po każdej zmiennej. Zwróciliśmy
na to uwagę już na początku rozdziału 14. Dlatego zasadne
jest poszukiwanie pozytywnych rozwiązań dla funkcji o innej
regularności.
razy po każdej zmiennej. Zwróciliśmy
na to uwagę już na początku rozdziału 14. Dlatego zasadne
jest poszukiwanie pozytywnych rozwiązań dla funkcji o innej
regularności.
Quasi-Monte Carlo jest deterministycznym odpowiednikiem klasycznej metody Monte Carlo dla aproksymacji całek na kostkach,
Definicja 15.1
Metoda quasi-Monte Carlo polega na przybliżeniu ![]() średnią arytmetyczną,
średnią arytmetyczną,
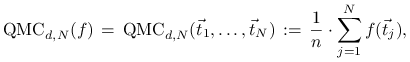 |
gdzie ![]() są pewnymi
szczególnymi punktami w
są pewnymi
szczególnymi punktami w ![]() wybranymi
w sposób deterministyczny.
wybranymi
w sposób deterministyczny.
Przez długi czas od swojego powstania uważano, że metody quasi-Monte Carlo są efektywne jedynie dla całek o niskich wymiarach. Dopiero pod koniec lat 90-tych ubiegłego wieku zauważono, że dają istotnie lepsze wyniki niż Monte Carlo w obliczaniu wartości niektórych instrumentów finansowych. Obecnie quasi-Monte Carlo jest powszchnie uznaną i bardzo popularną metodą, której znaczenie trudno przecenić mimo, że dotychczas nie udało się znaleźć pełnego teoretycznego wytłumaczenia jej efektywności.
15.2. Dyskrepancja
Rozważania na temat quasi-Monte Carlo zaczniemy od zdefiniowania pojęcia dyskrepancji, które odgrywa fundamentalną rolę w analizie efektywności tych metod.
Dla ![]() niech
niech
oznacza ![]() wymiarowy prostokąt w
wymiarowy prostokąt w ![]() , ,,zakotwiczony” w zerze.
Zakładamy przy tym, że
, ,,zakotwiczony” w zerze.
Zakładamy przy tym, że ![]() .
.
Definicja 15.2
Dyskrepancją (z gwiazdką) danego zbioru ![]() punktów
punktów
![]() ,
, ![]() , nazywamy wielkość
, nazywamy wielkość
gdzie
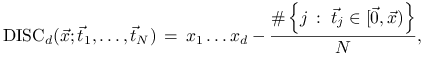 |
a ![]() oznacza liczbę elementów zbioru
oznacza liczbę elementów zbioru ![]() .
.
Ponieważ ![]() jest
jest ![]() -wymiarową objętością
prostokąta
-wymiarową objętością
prostokąta ![]() , dyskrepancja pokazuje jak
dobrze danych
, dyskrepancja pokazuje jak
dobrze danych ![]() punktów aproksymuje objętości tych
prostokątów.
Równoważnie, oznaczając przez
punktów aproksymuje objętości tych
prostokątów.
Równoważnie, oznaczając przez ![]() funkcję charakterystyczną prostokąta
funkcję charakterystyczną prostokąta ![]() mamy
mamy
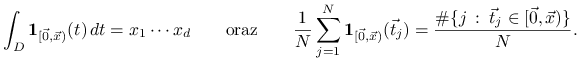 |
Stąd dyskrepancję można również interpretować jako maksymalny błąd aproksymacji funkcji charakterystycznych prostokątów przez odpowiedni algorytm quasi-Monte Carlo.
Pojęcie dyskrepancji zilustrujemy najpierw na przykładzie
jednowymiarowym ![]() . Nietrudno pokazać, że dla dowolnych
. Nietrudno pokazać, że dla dowolnych ![]()
| (15.1) |
Rzeczywiście, ![]() jako funkcja
jako funkcja ![]() ma
na każdym z przedziałów
ma
na każdym z przedziałów ![]() ,
, ![]() ,
, ![]() ,
pochodną równą
,
pochodną równą ![]() , oraz przyjmuje zero dla
, oraz przyjmuje zero dla ![]() .
Zatem, jeśli dyskrepancja byłaby mniejsza od
.
Zatem, jeśli dyskrepancja byłaby mniejsza od ![]() to mielibyśmy
to mielibyśmy
a stąd
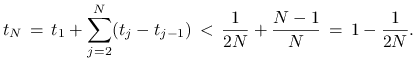 |
Otrzymujemy sprzeczność, bo dla ![]()
Z dowodu wynika, że równość w (15.1) zachodzi jedynie dla równomiernego rozmieszczenia punktów,
W tym przypadku algorytm ![]() redukuje się do zasady
punktu środkowego.
redukuje się do zasady
punktu środkowego.
Z punktu widzenia praktycznych obliczeń dobrze byłoby mieć ciąg nieskończony
i konstruować kolejne aproksymacje używając ![]() początkowych
wyrazów tego ciągu. Ciekawe, że wtedy zbieżność
początkowych
wyrazów tego ciągu. Ciekawe, że wtedy zbieżność
![]() nie może być zachowana. Dokładniej, można pokazać
istnienie
nie może być zachowana. Dokładniej, można pokazać
istnienie ![]() takiego, że dla każdego ciągu nierówność
takiego, że dla każdego ciągu nierówność
zachodzi dla nieskończenie wielu ![]() .
.
Analiza dyskrepancji w wymiarach ![]() just dużo bardziej
skomplikowana. Na razie ograniczymy się do zauważenia, że
siatka równomierna jest fatalnym wyborem. Dokładniej, niech
just dużo bardziej
skomplikowana. Na razie ograniczymy się do zauważenia, że
siatka równomierna jest fatalnym wyborem. Dokładniej, niech
będzie równomiernym rozkładem ![]() punktów w
punktów w ![]() .
Rozpatrzenie prostokąta
.
Rozpatrzenie prostokąta
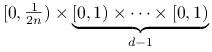 |
wystarcza, aby się przekonać, że wtedy dyskrepancja wynosi
co najmniej ![]() .
.
15.3. Błąd quasi-Monte Carlo
15.3.1. Formuła Zaremby
Jeśli ![]() jest funkcją różniczkowalną to
dla każdego
jest funkcją różniczkowalną to
dla każdego ![]() mamy
mamy
![f(x)\,=\, f(1)-\int _{x}^{1}f^{{\prime}}(t)\, dt\,=\, f(1)-\int _{0}^{1}{\bf 1}_{{(x,1]}}(t)\, f^{{\prime}}(t)\, dt.](wyklady/mo2/mi/mi2651.png) |
(15.2) |
Wzór ten uogólnimy na przypadek funkcji wielu zmiennych w następujący sposób.
Najpierw wprowadzimy kilka niezbędnych oznaczeń.
Dla podzbioru indeksów ![]() ,
,
niech ![]() , gdzie
, gdzie ![]() jest liczbą
elementów w
jest liczbą
elementów w ![]() . Niech dalej
. Niech dalej ![]() będzie
wektorem powstałym z wektora
będzie
wektorem powstałym z wektora
![]() poprzez usunięcie współrzędnych
poprzez usunięcie współrzędnych ![]() z
z ![]() ,
a
,
a ![]() wektorem, którego
wektorem, którego ![]() -ta
współrzędna wynosi
-ta
współrzędna wynosi ![]() dla
dla ![]() oraz wynosi
oraz wynosi
![]() dla
dla ![]() . Na przykład, jeśli
. Na przykład, jeśli ![]() i
i ![]() to dla
to dla ![]() mamy
mamy ![]() i
i ![]() .
.
W końcu, niech
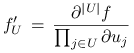 |
będzie skrótowym zapisem odpowiedniej pochodnej
mieszanej funkcji ![]() .
.
Lemat 15.1
Jeśli funkcja ![]() ma ciągłe pochodne
cząstkowe mieszane
ma ciągłe pochodne
cząstkowe mieszane ![]() dla wszystkich
dla wszystkich
![]() to
to
![f(\vec{x})\,=\, f(\vec{1})\,+\,\sum _{U}(-1)^{{|U|}}\int _{{D_{U}}}{\bf 1}_{{(\vec{x}_{U},\vec{1}_{U}]}}(\vec{z}_{U})\, f_{U}^{{\prime}}(\vec{z}_{U};1)\, d\vec{z}_{U},\qquad\vec{x}\in D](wyklady/mo2/mi/mi2605.png) |
(15.3) |
(![]() ).
).
Dowód
Dowód przeprowadzimy przez indukcję względem ![]() . Dla
. Dla
![]() równość (15.3) jest równoważna
(15.2).
Niech więc
równość (15.3) jest równoważna
(15.2).
Niech więc ![]() . Stosując założenie indukcyjne do
. Stosując założenie indukcyjne do
![]() z ustaloną ostatnią współrzędną
z ustaloną ostatnią współrzędną ![]() mamy
mamy
![f(\vec{x})\;=\; f(\vec{x}_{{\{ d\}}};1)\,+\,\sum _{V}(-1)^{{|V|}}\int _{{D_{V}}}{\bf 1}_{{(\vec{x}_{V},\vec{1}_{V}]}}(\vec{z}_{V})\, f_{V}^{{\prime}}(\vec{z}_{V},x_{d};1)\, d\vec{z}_{V},](wyklady/mo2/mi/mi2586.png) |
gdzie sumowanie jest po wszystkich
![]() .
Stosując dalej wzór (15.2) ze względu na
.
Stosując dalej wzór (15.2) ze względu na ![]() odpowiednio do
odpowiednio do ![]() i
i ![]() dostajemy
dostajemy
![\displaystyle f(\vec{1})\,-\,\int _{{D_{{\{ d\}}}}}{\bf 1}_{{\left(\vec{x}_{{\{ d\}}},\vec{1}_{{\{ d\}}}\right]}}\left(\vec{z}_{{\{ d\}}}\right)\, f_{{\{ d\}}}^{{\prime}}\left(\vec{z}_{{\{ d\}}};1\right)\, d\vec{z}_{{\{ d\}}}](wyklady/mo2/mi/mi2636.png) |
||||
![\displaystyle+\sum _{{V\cup\{ d\}}}(-1)^{{|V\cup\{ d\}|}}\int _{{D_{{V\cup\{ d\}}}}}{\bf 1}_{{\left(\vec{x}_{{V\cup\{ d\}}},\vec{1}_{{V\cup\{ d\}}}\right]}}\left(\vec{z}_{{V\cup\{ d\}}}\right)\, f_{{V\cup\{ d\}}}^{{\prime}}\left(\vec{z}_{{V\cup\{ d\}}};1\right)\, d\vec{z}_{{V\cup\{ d\}}}.](wyklady/mo2/mi/mi2678.png) |
Teraz wystarczy porównać otrzymaną formułę do prawej strony
(15.3). Drugi składnik odpowiada ![]() , trzeci
składnik podzbiorom
, trzeci
składnik podzbiorom ![]() do których nie należy
do których nie należy ![]() ,
a czwarty podzbiorom
,
a czwarty podzbiorom ![]() takim, że
takim, że ![]() i
i ![]() .
.
Zauważmy, że rozwijając ![]() i
i ![]() zgodnie
ze wzorem (15.3) mamy
zgodnie
ze wzorem (15.3) mamy
![\int _{D}f(\vec{x})\, d\vec{x}\,=\, f(\vec{1})+\sum _{U}(-1)^{{|U|}}\int _{{D_{U}}}\left(\int _{D}{\bf 1}_{{(\vec{x}_{U},\vec{1}_{U}]}}(\vec{z}_{U})\, d\vec{x}\right)\, f_{U}^{{\prime}}(\vec{z}_{U};1)\, d\vec{z}_{U},](wyklady/mo2/mi/mi2598.png) |
![\frac{1}{N}\,\sum _{{j=1}}^{N}f(\vec{t}_{j})\,=\, f(\vec{1})+\sum _{U}(-1)^{{|U|}}\int _{{D_{U}}}\left(\frac{1}{N}\sum _{{j=1}}^{N}{\bf 1}_{{((\vec{t}_{j})_{U},\vec{1}_{U}]}}(\vec{z}_{U})\right)\, f_{U}^{{\prime}}(\vec{z}_{U};1)\, d\vec{z}_{U}.](wyklady/mo2/mi/mi2648.png) |
Ponieważ wartość funkcji charakterystycznej odcinka
![]() w punkcie
w punkcie ![]() jest równa wartości funkcji
charakterystycznej odcinka
jest równa wartości funkcji
charakterystycznej odcinka ![]() w punkcie
w punkcie ![]() to
to
![\int _{D}{\bf 1}_{{(\vec{x}_{U},\vec{1}_{U}]}}(\vec{z}_{U})\, d\vec{x}\,=\,\int _{{D_{U}}}{\bf 1}_{{[\vec{0}_{U},\vec{z}_{U})}}(\vec{x}_{U})\, d\vec{x}_{U}\,=\,\prod _{{j\in U}}z_{j},](wyklady/mo2/mi/mi2568.png) |
![\frac{1}{N}\,\sum _{{j=1}}^{N}{\bf 1}_{{((\vec{t}_{j})_{U},\vec{1}_{U}]}}(\vec{z}_{U})\,=\,\frac{1}{N}\,\#\left\{ j\,:\;(\vec{t}_{j})_{U}\in[\vec{0}_{U},\vec{z}_{U})\right\}\,=\,\frac{1}{N}\,\#\left\{ j\,:\;\vec{t}_{j}\in\left[\vec{0},(\vec{z}_{U};1)\right)\right\}.](wyklady/mo2/mi/mi2567.png) |
Stąd otrzymujemy następującą formułę Zaremby na błąd quasi-Monte Carlo:
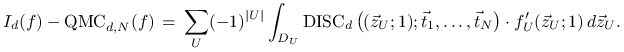 |
(15.4) |
15.3.2. Nierówność Koksmy-Hlawki
Oznaczmy przez ![]() klasę funkcji
klasę funkcji ![]() ,
których pochodne mieszane
,
których pochodne mieszane ![]() istnieją i są ciągłe
dla wszystkich
istnieją i są ciągłe
dla wszystkich ![]() .
.
Definicja 15.3
Wahaniem (w sensie Hardy-Krause) funkcji
![]() nazywamy wielkość
nazywamy wielkość
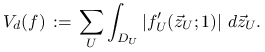 |
Zauważmy, że dla ![]() ,
,
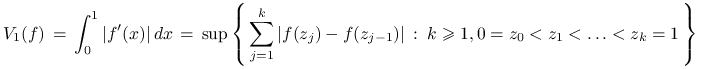 |
jest wahaniem funkcji w klasycznym sensie. Następujące bardzo ważne oszacowanie błędu metody quasi-Monte Carlo nosi nazwę nierówności Koksmy-Hlawki.
Twierdzenie 15.1
Jeśli ![]() to błąd metody quasi-Monte Carlo
to błąd metody quasi-Monte Carlo
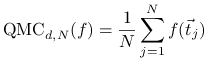 |
dla aproksymacji całki ![]() szacuje się przez
szacuje się przez
W nierówności Koksmy-Hlawki czynnik błędu ![]() zależny
jedynie od funkcji jest oddzielony od czynnika błędu
zależny
jedynie od funkcji jest oddzielony od czynnika błędu
![]() zależnego od wyboru
punktów. O ile nie mamy wpływu na wahanie funkcji, możemy
starać się wybrać punkty
zależnego od wyboru
punktów. O ile nie mamy wpływu na wahanie funkcji, możemy
starać się wybrać punkty ![]() tak, aby zminimalizować
ich dyskrepancję. Zasadnicze pytanie brzmi: jak mała może być
dyskrepacja? W szczególności, czy można wybrać nieskończony
ciąg punktów tak, że oparte na nim algorytmy quasi-Monte Carlo
pokonują przekleństwo wymiaru w klasie
tak, aby zminimalizować
ich dyskrepancję. Zasadnicze pytanie brzmi: jak mała może być
dyskrepacja? W szczególności, czy można wybrać nieskończony
ciąg punktów tak, że oparte na nim algorytmy quasi-Monte Carlo
pokonują przekleństwo wymiaru w klasie ![]() ?
?
Na miejscu jest teraz uwaga, że dzięki obecności pochodnych
mieszanych rozumowanie analogiczne do tego z dowodu
twierdzenia 13.4 prowadzi w klasie funkcji
![]() z
z ![]() jedynie do oszacowania
z dołu błędu przez
jedynie do oszacowania
z dołu błędu przez ![]() (a nie
(a nie ![]() ).
).
Okazuje się, że pełne odpowiedzi na zadane pytania
nie są znane. Najlepsze ciągi nieskończone
![]() spełniają nierówność
spełniają nierówność
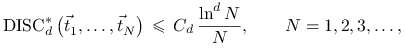 |
gdzie ![]() nie zależy od
nie zależy od ![]() .
.
Wydaje się więc, że w klasie ![]() metody quasi-Monte Carlo dają istotnie lepsze wyniki od
Monte Carlo, bo błąd nie tylko jest deterministyczny, ale
też dla
metody quasi-Monte Carlo dają istotnie lepsze wyniki od
Monte Carlo, bo błąd nie tylko jest deterministyczny, ale
też dla ![]() zbiega do zera dużo szybciej,
tzn. błąd jest rzędu
zbiega do zera dużo szybciej,
tzn. błąd jest rzędu ![]() dla dowolnego
dla dowolnego
![]() w przypadku quasi-Monte Carlo, oraz
w przypadku quasi-Monte Carlo, oraz ![]() w przypadku Monte Carlo. Nie do końca jest to prawdą.
Zauważmy bowiem, że w praktycznych obliczeniach wnioski
asymptotyczne nie mają zastosowania, gdy wymiar
w przypadku Monte Carlo. Nie do końca jest to prawdą.
Zauważmy bowiem, że w praktycznych obliczeniach wnioski
asymptotyczne nie mają zastosowania, gdy wymiar ![]() jest
bardzo duży. Wtedy czynnik
jest
bardzo duży. Wtedy czynnik ![]() może mieć istotne znaczenie
i wręcz sprawiać, że nierówność Koksmy-Hlawki staje się
bezużyteczna. Dodatkowo, dobre oszacowanie
może mieć istotne znaczenie
i wręcz sprawiać, że nierówność Koksmy-Hlawki staje się
bezużyteczna. Dodatkowo, dobre oszacowanie ![]() jest wyjątkowe
trudne.
jest wyjątkowe
trudne.
A jednak metody quasi-Monte Carlo są z powodzeniem stosowane
w praktyce obliczeniowej nawet dla dużych wymiarów ![]() .
Istnieje wiele hipotez tworzonych w celu wyjaśnienia tego
pozornego paradoksu. Jedna z najbardziej popularnych i już
dość dobrze uzasadnionych teoretycznie mówi, że w praktyce
mamy co prawda do czynienia z funkcjami bardzo wielu zmiennych,
ale istotnych jest jedynie kilka zmiennych albo grupy kilku
zmiennych. Matematycznie oznacza to, że w odpowiadających
tym założeniom przestrzeniach zachodzą dużo mocniejsze
odpowiedniki nierówności Koksmy-Hlawki.
.
Istnieje wiele hipotez tworzonych w celu wyjaśnienia tego
pozornego paradoksu. Jedna z najbardziej popularnych i już
dość dobrze uzasadnionych teoretycznie mówi, że w praktyce
mamy co prawda do czynienia z funkcjami bardzo wielu zmiennych,
ale istotnych jest jedynie kilka zmiennych albo grupy kilku
zmiennych. Matematycznie oznacza to, że w odpowiadających
tym założeniom przestrzeniach zachodzą dużo mocniejsze
odpowiedniki nierówności Koksmy-Hlawki.
15.4. Ciągi o niskiej dyskrepancji
Definicja 15.4
Ciąg nieskończony ![]() nazywamy ciągem o niskiej dyskrepancji jeśli istnieje
nazywamy ciągem o niskiej dyskrepancji jeśli istnieje
![]() taka, że dla wszystkich
taka, że dla wszystkich ![]()
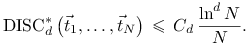 |
Istnieje bardzo dużo efektywnych konstrukcji ciągów punktów o niskiej dyskrepancji. Teraz poznamy jedynie kilka najbardziej popularnych z nich.
15.4.1. Ciąg Van der Corputa
Niech ![]() będzie ustaloną liczbą naturalną. Wtedy
dowolną liczbę naturalną
będzie ustaloną liczbą naturalną. Wtedy
dowolną liczbę naturalną ![]() można jednoznacznie przedstawić
w postaci
można jednoznacznie przedstawić
w postaci
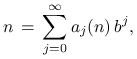 |
gdzie ![]() i tylko dla skończonej liczby
indeksów
i tylko dla skończonej liczby
indeksów ![]() mamy
mamy ![]() . Mówiąc inaczej,
. Mówiąc inaczej, ![]() są
kolejnymi cyframi rozwinięcia liczby
są
kolejnymi cyframi rozwinięcia liczby ![]() w bazie
w bazie ![]() .
Wykorzystując powyższe rozwinięcie funkcję radykalnej
odwrotności
.
Wykorzystując powyższe rozwinięcie funkcję radykalnej
odwrotności ![]() definujemy jako
definujemy jako
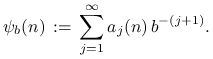 |
Na przykład, dla bazy ![]() mamy
mamy ![]() ,
czyli
,
czyli ![]() .
.
Kolejne wartości radykalnej odwrotności,
tworzą jednowymiarowy ciąg Van der Corputa.
Dla ![]() kolejne punkty ciągu wynoszą więc
kolejne punkty ciągu wynoszą więc
Ciąg Van der Corputa jest ciągiem o niskiej dyskrepancji dla dowolnie
dobranej bazy ![]() , tzn. dyskrepancja
, tzn. dyskrepancja ![]() początkowych wyrazów szacuje
się z góry przez
początkowych wyrazów szacuje
się z góry przez ![]() . Zauważmy jednak, że dla
. Zauważmy jednak, że dla ![]() ,
,
![]() , dostajemy równomierne rozmieszczenie punktów, tzn. tworzą
one zbiór
, dostajemy równomierne rozmieszczenie punktów, tzn. tworzą
one zbiór ![]() , którego dyskrepancja wynosi
, którego dyskrepancja wynosi
![]() . Stąd, pożądane są raczej mniejsze bazy
. Stąd, pożądane są raczej mniejsze bazy ![]() ; im
większe
; im
większe ![]() tym rzadziej ze względu na
tym rzadziej ze względu na ![]() osiągana jest dyskrepancja
proporcjonalna do
osiągana jest dyskrepancja
proporcjonalna do ![]() .
.
15.4.2. Konstrukcje Haltona i Sobol'a
Jednowymiarowy ciąg Van der Corputa jest podstawą konstrukcji wielu
ciągów w wyższych wymiarach ![]() . Jedna z nich prowadzi do ciągu
Haltona
. Jedna z nich prowadzi do ciągu
Haltona ![]() , którego
, którego ![]() -ty punkt wynosi
-ty punkt wynosi
Liczby ![]() są tu danymi bazami. Od razu zauważamy, że
wybór
są tu danymi bazami. Od razu zauważamy, że
wybór ![]() nie jest dobry, bo prowadzi do siatki równomiernej
w
nie jest dobry, bo prowadzi do siatki równomiernej
w ![]() , zob. rozdział 15.2. Jeśli jednak
, zob. rozdział 15.2. Jeśli jednak ![]() są
liczbami pierwszymi to
są
liczbami pierwszymi to ![]() jest już ciągiem o niskiej
dyskrepancji.
jest już ciągiem o niskiej
dyskrepancji.
Minusem konstrukcji Haltona jest to, że dla dużych wymiarów ![]() bazy
bazy
![]() też są duże co, jak wcześniej zauważyliśmy, nie jest korzystne.
Problemu tego unika bardziej skomplikowana konstrukcja Sobol'a,
gdzie na każdej zmiennej pracujemy z tą samą bazą
też są duże co, jak wcześniej zauważyliśmy, nie jest korzystne.
Problemu tego unika bardziej skomplikowana konstrukcja Sobol'a,
gdzie na każdej zmiennej pracujemy z tą samą bazą ![]() .
.
Ideę konstrukcji ciągu Sobol'a ![]() przedstawimy najpierw
zakładając
przedstawimy najpierw
zakładając ![]() . Niech
. Niech
będzie wektorem kolejnych bitów w rozwinięciu dwójkowym liczby ![]() ,
,
Wtedy
gdzie
![\left[\begin{array}[]{c}y_{1}(k)\\
y_{2}(k)\\
\vdots\\
y_{r}(k)\end{array}\right]\,=\, V\cdot\left[\begin{array}[]{c}a_{0}(k)\\
a_{1}(k)\\
\vdots\\
a_{{r-1}}(k)\end{array}\right]\;\mbox{mod}\; 2,](wyklady/mo2/mi/mi2638.png) |
a ![]() jest specjalnie dobraną macierzą o elementach
jest specjalnie dobraną macierzą o elementach ![]() i
i ![]() , zwaną
macierzą generującą. (Zauważmy, że jeśli
, zwaną
macierzą generującą. (Zauważmy, że jeśli ![]() jest identycznością
to otrzymany ciąg jest ciągiem Van der Corputa.)
jest identycznością
to otrzymany ciąg jest ciągiem Van der Corputa.)
Oznaczając ![]() możemy równoważnie zapisać
możemy równoważnie zapisać
gdzie ![]() jest operacją XOR, czyli dodawaniem bitów modulo
jest operacją XOR, czyli dodawaniem bitów modulo ![]() ,
,
Dla ![]() , kolejne współrzędne punktu
, kolejne współrzędne punktu ![]() wyliczane
są według powyższej recepty, ale używając różnych macierzy
generujących
wyliczane
są według powyższej recepty, ale używając różnych macierzy
generujących ![]() . I właśnie problem wyboru macierzy generujących tak,
aby otrzymać ciąg o niskiej dyskrepancji jest istotą konstrukcji Sobol'a.
Dodajmy, że jest to problem wysoce nietrywialny.
. I właśnie problem wyboru macierzy generujących tak,
aby otrzymać ciąg o niskiej dyskrepancji jest istotą konstrukcji Sobol'a.
Dodajmy, że jest to problem wysoce nietrywialny.
15.4.3. Sieci 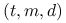 i ciągi
i ciągi 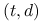
Dla ![]() definiujemy
definiujemy ![]() -prostokąt w
-prostokąt w ![]() jako
jako
gdzie ![]() ,
, ![]() ,
,
![]() . Na przykład, jeśli
. Na przykład, jeśli ![]() i
i ![]() to przedziały
to przedziały
![]() i
i ![]() są
są ![]() -prostokątami, ale nie jest nim
-prostokątami, ale nie jest nim ![]() .
Zauważmy, że objętość
.
Zauważmy, że objętość ![]() -prostokąta wynosi
-prostokąta wynosi ![]() .
.
Definicja 15.5
Niech ![]() i
i ![]() . Siecią
. Siecią ![]() w bazie
w bazie ![]() nazywamy
zbiór
nazywamy
zbiór ![]() punktów w
punktów w ![]() o własności, że w każdym
o własności, że w każdym
![]() -prostokącie o objętości
-prostokącie o objętości ![]() znajduje się dokładnie
znajduje się dokładnie ![]() punktów tego zbioru.
punktów tego zbioru.
Mówiąc inaczej, sieć ![]() dokładnie pokazuje objętości
dokładnie pokazuje objętości
![]() -prostokątów poprzez iloraz
-prostokątów poprzez iloraz ![]() liczby punktów, które
należą do prostokąta do liczby wszystkich punktów.
liczby punktów, które
należą do prostokąta do liczby wszystkich punktów.
Definicja 15.6
Ciąg nieskończony ![]() w
w ![]() nazywamy
ciągiem
nazywamy
ciągiem ![]() w bazie
w bazie ![]() jeśli dla wszystkich
jeśli dla wszystkich
![]() i
i ![]() segment
segment
jest siecią ![]() w bazie
w bazie ![]() .
.
Następujące twierdzenie jest podstawą wielu konstrukcji ciągów o niskiej dyskrepancji.
Twierdzenie 15.2
Każdy ciąg ![]() w bazie
w bazie ![]() jest ciągiem o niskiej dyskrepancji.
jest ciągiem o niskiej dyskrepancji.
Pokazanie konkretnych konstrukcji ciągów ![]() wykracza poza ramy
tego wykładu. Powiemy tylko, że szczególne wybory macierzy generujących
w konstrukcji Sobol'a prowadzą do ciągów
wykracza poza ramy
tego wykładu. Powiemy tylko, że szczególne wybory macierzy generujących
w konstrukcji Sobol'a prowadzą do ciągów ![]() . Inne konstrukcje
należą do Faure'a, Niederreitera, Tezuki i in.
. Inne konstrukcje
należą do Faure'a, Niederreitera, Tezuki i in.