Zagadnienia
2. Zagadnienie własne II
Kolejne dwa wykłady poświęcimy konkretnym metodom numerycznym rozwiązywania zagadnienia własnego.
2.1. Uwagi wstępne
Ponieważ wartości własne macierzy ![]() są zerami
jej wielomianu charakterystycznego, narzucająca się
metoda poszukiwania wartości własnych polegałaby
na wyliczeniu współczynników tego wielomianu,
na przykład w bazie potęgowej, a następnie na zastosowaniu
jednej ze znanych metod znajdowania zer wielomianu. Dla wielomianów
o współczynnikach rzeczywistych mogłaby to być np. metoda
bisekcji, metoda Newtona (siecznych), albo pewna kombinacja obu method.
Należy jednak przestrzec przed dokładnie takim postępowaniem.
Rzecz w tym, że zera wielomianu mogą być bardzo wrażliwe
na zaburzenia jego współczynnikówi. Dobrze ilustruje to
następujący przykład.
są zerami
jej wielomianu charakterystycznego, narzucająca się
metoda poszukiwania wartości własnych polegałaby
na wyliczeniu współczynników tego wielomianu,
na przykład w bazie potęgowej, a następnie na zastosowaniu
jednej ze znanych metod znajdowania zer wielomianu. Dla wielomianów
o współczynnikach rzeczywistych mogłaby to być np. metoda
bisekcji, metoda Newtona (siecznych), albo pewna kombinacja obu method.
Należy jednak przestrzec przed dokładnie takim postępowaniem.
Rzecz w tym, że zera wielomianu mogą być bardzo wrażliwe
na zaburzenia jego współczynnikówi. Dobrze ilustruje to
następujący przykład.
Przykład 2.1
Załóżmy, że ![]() jest macierzą symetryczną
formatu
jest macierzą symetryczną
formatu ![]() o wartościach własnych
o wartościach własnych ![]() .
Zapisując wielomian charakterystyczny
w postaci potęgowej mamy
.
Zapisując wielomian charakterystyczny
w postaci potęgowej mamy
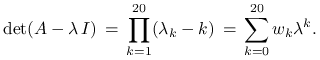 |
Okazuje się, że zaburzenie współczynnika ![]() mogą
powodować
mogą
powodować ![]() razy większe zaburzenie wartości własnej
razy większe zaburzenie wartości własnej
![]() .
.
Nie znaczy to oczywiście, że metody bazujące na obliczaniu
wielomianu charakterystycznego, czy jego pochodnych trzeba z gruntu
odrzucić. Trzeba tylko pamiętać, aby przy obliczeniach korzystać
bezpośrednio ze współczynników ![]() macierzy
macierzy ![]() , ponieważ,
jak wiemy z poprzedniego rozdziału, zadanie jest ze względu na te
współczynniki dobrze uwarunkowane.
, ponieważ,
jak wiemy z poprzedniego rozdziału, zadanie jest ze względu na te
współczynniki dobrze uwarunkowane.
Z drugiej strony zauważmy, że policzenie wyznacznika macierzy pełnej wprost z definicji jest raczej kosztowne. Dlatego w praktyce metody wyznacznikowe są zwykle poprzedzone prekomputingiem polegającym na sprowadzeniu macierzy przez podobieństwa ortogonalne do prostszej postaci, z której wyznacznik można już obliczyć dużo tańszym kosztem niż dla macierzy pełnej. Tego typu precomputing ma również zastosowanie w innych metodach, w którym np. trzeba wykonywać mnożenie macierzy przez wektor.
Jedną z takich wygodnych postaci macierzy jest postać Hessenberga, a dla macierzy hermitowskich postać trójdiagonalna.
2.1.1. Sprowadzanie macierzy do postaci Hessenberga
Macierz ![]() jest postaci Hessenberga
(,,prawie” trójkątną górną) jeśli wszystkie wyrazy
jest postaci Hessenberga
(,,prawie” trójkątną górną) jeśli wszystkie wyrazy ![]() dla
dla
![]() są zerami, tzn.
są zerami, tzn.
![A\,=\,\left[\begin{array}[]{ccccc}a_{{1,1}}&a_{{1,2}}&\cdots&a_{{1,n-1}}&a_{{1,n}}\\
a_{{2,1}}&a_{{2,2}}&\cdots&a_{{2,n-1}}&a_{{2,n}}\\
0&a_{{3,2}}&\cdots&a_{{3,n-1}}&a_{{3,n}}\\
\vdots&\vdots&&\vdots&\vdots\\
0&0&\cdots&a_{{n,n-1}}&a_{{n,n}}\end{array}\right].](wyklady/mo2/mi/mi359.png) |
Oczywiście, jeśli macierz jest hermitowska, ![]() , to postać Hessenberga
jest równoważna postaci trójdiagonalnej
, to postać Hessenberga
jest równoważna postaci trójdiagonalnej
![A\,=\,\left[\begin{array}[]{ccccc}c_{1}&b_{2}&0&\cdots&0\\
\overline{b}_{2}&c_{2}&b_{3}&\cdots&0\\
0&\overline{b}_{3}&c_{3}&\cdots&0\\
\vdots&\vdots&\vdots&&\vdots\\
0&0&\cdots&\cdots&c_{n}\end{array}\right].](wyklady/mo2/mi/mi282.png) |
(2.1) |
Aby daną macierz ![]() sprowadzić do postaci Hessenberga przez
podobieństwa ortogonalne (a więc nie zmieniając wartości
własnych), możemy zastosować znane nam odbicia Householdera.
Przypomnijmy, że dla dowolnego niezerowego wektora
sprowadzić do postaci Hessenberga przez
podobieństwa ortogonalne (a więc nie zmieniając wartości
własnych), możemy zastosować znane nam odbicia Householdera.
Przypomnijmy, że dla dowolnego niezerowego wektora ![]() istnieje macierz ortogonalna (odbicie Householdera)
istnieje macierz ortogonalna (odbicie Householdera)
![]() postaci
postaci ![]() ,
gdzie
,
gdzie ![]() , która przekształca
, która przekształca ![]() na kierunek
pierwszego wersora, tzn.
na kierunek
pierwszego wersora, tzn.
![]() ,
, ![]() .
(Odbicia Householdera zostały dokładnie przedstawione na wykładzie
Analiza Numeryczna I.)
.
(Odbicia Householdera zostały dokładnie przedstawione na wykładzie
Analiza Numeryczna I.)
Niech ![]() będzie dowolną macierzą.
Algorytm konstruuje najpierw odbicie
będzie dowolną macierzą.
Algorytm konstruuje najpierw odbicie ![]() dla wektora
dla wektora
![]() , a następnie biorąc macierz
, a następnie biorąc macierz
![\widehat{P}_{1}=\left[\begin{array}[]{cc}1&\vec{0}^{{\, T}}\\
\vec{0}&P_{1}\end{array}\right]\in\mathbb{C}^{{n,n}}](wyklady/mo2/mi/mi384.png) |
oblicza ![]() . łatwo zobaczyć, że
wtedy elementy
. łatwo zobaczyć, że
wtedy elementy ![]() dla
dla ![]() w macierzy
w macierzy ![]() są
równe zeru.
są
równe zeru.
Postępując indukcyjnie załóżmy, że dostaliśmy już macierz
![]() ,
, ![]() , w której elementy
, w której elementy
![]() dla
dla ![]() ,
, ![]() , są wyzerowane.
W kroku
, są wyzerowane.
W kroku ![]() -szym algorytm konstruuje odbicie
-szym algorytm konstruuje odbicie
![]() dla wektora
dla wektora
![]() , a następnie biorąc macierz
, a następnie biorąc macierz
oblicza ![]() .
Wtedy wszystkie elementy
.
Wtedy wszystkie elementy ![]() dla
dla ![]() ,
, ![]() ,
są zerami. Po
,
są zerami. Po ![]() krokach otrzymana macierz
krokach otrzymana macierz
![]() jest postaci Hessenberga.
jest postaci Hessenberga.
Jasne jest, że jeśli ![]() to opisany algorytm prowadzi do
macierzy trójdiagonalnej,
to opisany algorytm prowadzi do
macierzy trójdiagonalnej, ![]() .
(Obliczenia można wtedy w każdym kroku wykonywać jedynie
na głównej diagonali i pod nią.)
.
(Obliczenia można wtedy w każdym kroku wykonywać jedynie
na głównej diagonali i pod nią.)
Dodajmy jeszcze, że koszt sprowadzenia macierzy przez podobieństwa
ortogonalne do postaci Hessenberga/trójdiagonalnej jest proporcjonalny
do ![]() .
.
2.2. Metoda Hymana
Przy pomocy metody Hymana możemy w zręczny sposób obliczyć
wartości i pochodne wielomianu charakterystycznego ![]() dla
macierzy Hessenberga
dla
macierzy Hessenberga ![]() Bez zmniejszenia ogólności
będziemy zakładać, że wszystkie elementy
Bez zmniejszenia ogólności
będziemy zakładać, że wszystkie elementy ![]() . W przeciwnym
przypadku wyznacznik można obliczyć jako iloczyn wyznaczników macierzy
Hessenberga niższych rzędów.
. W przeciwnym
przypadku wyznacznik można obliczyć jako iloczyn wyznaczników macierzy
Hessenberga niższych rzędów.
Metoda Hymana polega na dodaniu do pierwszego wiersza macierzy ![]() wiersza
wiersza ![]() -tego pomnożonego przez pewien współczynnik
-tego pomnożonego przez pewien współczynnik ![]() ,
dla
,
dla ![]() tak, aby wyzerować elementy
tak, aby wyzerować elementy ![]() dla
dla ![]() .
Ponieważ
.
Ponieważ
![A-\lambda\, I\,=\,\left[\begin{array}[]{ccccc}a_{{1,1}}-\lambda&a_{{1,2}}&\cdots&a_{{1,n-1}}&a_{{1,n}}\\
a_{{2,1}}&a_{{2,2}}-\lambda&\cdots&a_{{2,n-1}}&a_{{2,n}}\\
0&a_{{3,2}}&\cdots&a_{{3,n-1}}&a_{{3,n}}\\
\vdots&\vdots&&\vdots&\vdots\\
0&0&\cdots&a_{{n,n-1}}&a_{{n,n}}-\lambda\end{array}\right],](wyklady/mo2/mi/mi253.png) |
mamy następujące równania na ![]() :
:
| (2.2) |
dla ![]() Stąd, definiując dodatkowo
Stąd, definiując dodatkowo ![]() , dostajemy
następujące równania rekurencyjne:
, dostajemy
następujące równania rekurencyjne:
Po opisanym przekształceniu macierzy ![]() zmieni się jedynie
jej pierwszy wiersz; wyrazy
zmieni się jedynie
jej pierwszy wiersz; wyrazy ![]() ,
, ![]() , zostaną wyzerowane,
a
, zostaną wyzerowane,
a ![]() zostanie przekształcony do
zostanie przekształcony do
Rozwijając wyznacznik względem (przekształconego) pierwszego wiersza otrzymujemy
a stąd zera wielomianu charakterystycznego są równe zerom wielomianu
Oczywiście, wartości ![]() można obliczać stosując wzory
rekurencyjne (2.2) przedłużając je o
można obliczać stosując wzory
rekurencyjne (2.2) przedłużając je o ![]() , przy dodatkowym
formalnym podstawieniu
, przy dodatkowym
formalnym podstawieniu ![]()
Aby móc zastowoać netodę Newtona (stycznych) do znalezienia zer wielomianu
![]() potrzebujemy również wiedzieć jak obliczać jego pochodne. To też
nie jest problem, bo rekurencyjne wzory na pochodne można uzyskać po prostu
różniczkując wzory (2.2). Dodajmy, że koszt obliczenia wartości
potrzebujemy również wiedzieć jak obliczać jego pochodne. To też
nie jest problem, bo rekurencyjne wzory na pochodne można uzyskać po prostu
różniczkując wzory (2.2). Dodajmy, że koszt obliczenia wartości
![]() i
i ![]() jest proporjonalny do
jest proporjonalny do ![]() ,
co jest istotnym zyskiem w porównaniu z kosztem
,
co jest istotnym zyskiem w porównaniu z kosztem ![]() obliczania wyznacznika
pełnej macierzy za pomocą faktoryzacji metodą eliminacji Gaussa.
obliczania wyznacznika
pełnej macierzy za pomocą faktoryzacji metodą eliminacji Gaussa.
Formuły na obliczanie wyznacznika ![]() i jego pochodnych
uproszczają się jeszcze bardziej gdy macierz
i jego pochodnych
uproszczają się jeszcze bardziej gdy macierz ![]() jest dodatkowo hermitowska,
czyli jest macierzą trójdiagonalną postaci (2.1). Wtedy, stosując
zwykłe rozumowanie rekurencyjne, łatwo się przekonać, że kolejne minory
główne (czyli wyznaczniki macierzy kątowych) spełniają zależności
jest dodatkowo hermitowska,
czyli jest macierzą trójdiagonalną postaci (2.1). Wtedy, stosując
zwykłe rozumowanie rekurencyjne, łatwo się przekonać, że kolejne minory
główne (czyli wyznaczniki macierzy kątowych) spełniają zależności
Różniczkując otrzymane wzory otrzymujemy formuły na pochodne kolejnych
minorów po ![]() . Wartości wielomianu
. Wartości wielomianu ![]() oraz jego pochodnych można więc obliczać kosztem liniowym w
oraz jego pochodnych można więc obliczać kosztem liniowym w ![]() .
.
Sprawę konkretnej implementacji metod iteracyjnych bisekcji i/lub Newtona
do wyznaczenia zer wielomianu ![]() tutaj pomijamy. Ograniczymy
się jedynie do stwierdzenia, że nie jest to rzecz całkiem trywialna.
tutaj pomijamy. Ograniczymy
się jedynie do stwierdzenia, że nie jest to rzecz całkiem trywialna.
2.3. Metoda potęgowa
2.3.1. Definicja metody
Metoda potęgowa zdefiniowana jest w następujący prosty sposób.
Rozpoczynając od dowolnego wektora ![]() o normie
o normie
![]() obliczamy kolejno dla
obliczamy kolejno dla ![]()
Równoważnie możemy napisać
Wektory ![]() stanowią kolejne przybliżenia wektora
własnego. Odpowiadającą mu wartość własną przybliżamy
wzorem
stanowią kolejne przybliżenia wektora
własnego. Odpowiadającą mu wartość własną przybliżamy
wzorem
2.3.2. Analiza zbieżności
Analizę metody potęgowej przeprowadzimy przy założeniu,
że macierz ![]() jest diagonalizowalna. Oznaczmy przez
jest diagonalizowalna. Oznaczmy przez ![]() ,
,
![]() , różne wartości własne macierzy
, różne wartości własne macierzy ![]() , a przez
, a przez
![]() odpowiadające im podprzestrzenie własne,
odpowiadające im podprzestrzenie własne,
| (2.3) |
Założymy, że ![]() jest dominującą wartością własną oraz
jest dominującą wartością własną oraz
Przedstawmy ![]() jednoznacznie w postaci
jednoznacznie w postaci
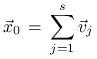 |
gdzie ![]() . Dla uproszczenia, będziemy
zakładać, że każda ze składowych
. Dla uproszczenia, będziemy
zakładać, że każda ze składowych
Podkreślmy, że nie jest to założenie ograniczające, bo
w przeciwnym przypadku składowe zerowe po prostu ignorujemy
w poniższej analizie zbieżności. Poza tym, jeśli wektor
początkowy jest wybrany losowo, to teoretyczne prawdopodobieństwo
takiego zdarzenia jest zerowe. Co więcej, nawet jeśli jedna ze
składowych znika to wskutek błędów zaokrągleń w procesie
obliczeniowym składowa ta w wektorze ![]() będzie
z pewnością niezerowa. (Mamy tu do czynienia z ciekawym
zjawiskiem, kiedy błędy zaokrągleń pomagają!)
będzie
z pewnością niezerowa. (Mamy tu do czynienia z ciekawym
zjawiskiem, kiedy błędy zaokrągleń pomagają!)
Prosty rachunek pokazuje, że
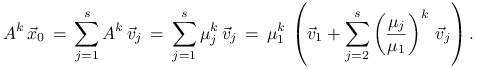 |
Ponieważ każdy z ilorazów ![]() to
to ![]() zbiega do wektora własnego
zbiega do wektora własnego ![]() , a
, a ![]() do dominującej wartości własnej
do dominującej wartości własnej ![]() . Przyjrzyjmy się
od czego zależy szybkość zbieżności.
. Przyjrzyjmy się
od czego zależy szybkość zbieżności.
Odległość ![]() wektora
wektora ![]() od podprzestrzeni
od podprzestrzeni ![]() można oszacować z góry przez
odległość
można oszacować z góry przez
odległość ![]() od
od ![]() , która z kolei
jest równa długości rzutu
, która z kolei
jest równa długości rzutu ![]() tego wektora na podprzestrzeń
ortogonalną do
tego wektora na podprzestrzeń
ortogonalną do ![]() ,
,
Oznaczając
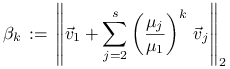 |
mamy ![]() oraz
oraz
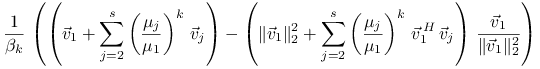 |
||||
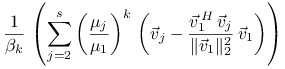 |
||||
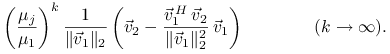 |
Biorąc normę i stosując nierówność trójkąta dostajemy
gdzie
Zbieżność jest więc liniowa z ilorazem ![]() .
.
Zobaczmy teraz jak bardzo ![]() różni się od
różni się od ![]() . Mamy
. Mamy
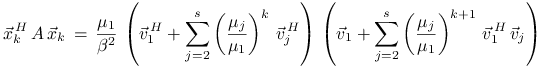 |
||||
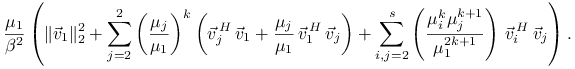 |
Stąd wynika, że błąd ![]() zależy od iloczynów skalarnych
zależy od iloczynów skalarnych
![]() oraz od stosunków
oraz od stosunków
Dokładniej, niech
albo ![]() jeśli powyższy zbiór jest pusty. Jeśli teraz
jeśli powyższy zbiór jest pusty. Jeśli teraz ![]() albo
mamy jednocześnie
albo
mamy jednocześnie ![]() i
i ![]() to
to
i zbieżność jest liniowa z ilorazem ![]() . Jeśli zaś
. Jeśli zaś ![]() i
i ![]() to
to
i zbieżność jest liniowa z ilorazem ![]() .
W szczególności, jeśli
.
W szczególności, jeśli ![]() to zbieżość jest
z ilorazem
to zbieżość jest
z ilorazem ![]() .
.
Dla macierzy rzeczywistych i symetrycznych możemy stosunkowo łatwo pokazać dokładne nierówności na błąd metody potęgowej.
Twierdzenie 2.1
Załóżmy, że macierz ![]() . Niech
. Niech ![]() będzie
kątem pomiędzy wektorem
będzie
kątem pomiędzy wektorem ![]() -tego przybliżenia
-tego przybliżenia ![]() otrzymanego
metodą potęgową i podprzestrzenią własną
otrzymanego
metodą potęgową i podprzestrzenią własną ![]() odpowiadającą dominującej wartości własnej
odpowiadającą dominującej wartości własnej ![]() . Wtedy
. Wtedy
oraz
Dowód
Ponieważ macierz jest symetryczna, podprzestrzenie własne ![]() zdefiniowane w (2.3) są parami ortogonalne. Dlatego
zdefiniowane w (2.3) są parami ortogonalne. Dlatego
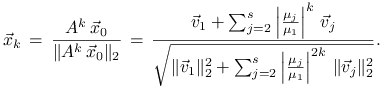 |
Tangens kąta ![]() jest równy stosunkowi długości składowej
wektora
jest równy stosunkowi długości składowej
wektora ![]() w podprzestrzeni
w podprzestrzeni
![]() do długości składowej tego wektora w podprzestrzeni
do długości składowej tego wektora w podprzestrzeni ![]() .
Mamy więc
.
Mamy więc
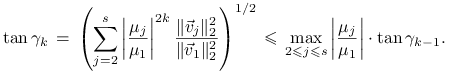 |
Aby pokazać pozostałą część twierdzenia, przedstawmy ![]() w postaci
w postaci
![]() , gdzie
, gdzie ![]() .
Wtedy
.
Wtedy ![]() oraz
oraz
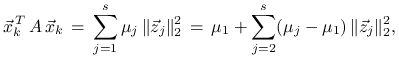 |
a stąd
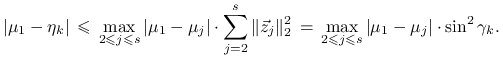 |
Przypomnijmy, że ![]() przy czym mamy asymptotyczną
równość gdy
przy czym mamy asymptotyczną
równość gdy ![]() . Ponieważ macierz
. Ponieważ macierz ![]() jest symetryczna to
mamy również
jest symetryczna to
mamy również ![]() . Z twierdzenia 2.1
wynika więc, że
. Z twierdzenia 2.1
wynika więc, że
Metoda potęgowa nie opłaca się gdy wymiar ![]() nie jest duży, albo
macierz
nie jest duży, albo
macierz ![]() jest pełna. Inaczej jest, gdy
jest pełna. Inaczej jest, gdy ![]() jest ,,wielkie”,
np. rzędu co najmniej kilkuset, a macierz
jest ,,wielkie”,
np. rzędu co najmniej kilkuset, a macierz ![]() jest rozrzedzona, tzn.
ma jedynie proporcjonalnie do
jest rozrzedzona, tzn.
ma jedynie proporcjonalnie do ![]() elementów niezerowych. Z taką
sytuacją mamy do czynienia, gdy np. macierz jest pięciodiagonalna.
Wtedy istotne dla metody mnożenie
elementów niezerowych. Z taką
sytuacją mamy do czynienia, gdy np. macierz jest pięciodiagonalna.
Wtedy istotne dla metody mnożenie ![]() można wykonać kosztem
proporcjonalnym do
można wykonać kosztem
proporcjonalnym do ![]() i poświęcając tyle samo pamięci
(wyrazy zerowe można zignorować).
i poświęcając tyle samo pamięci
(wyrazy zerowe można zignorować).
2.4. Odwrotna metoda potęgowa i deflacja
Odwrotna metoda potęgowa albo metoda Wielandta, polega na
zastosowaniu (prostej) metody potęgowej do macierzy ![]() .
Dokładniej, startując z przybliżenia początkowego
.
Dokładniej, startując z przybliżenia początkowego ![]() o jednostkowej
normie drugiej obliczamy kolejno dla
o jednostkowej
normie drugiej obliczamy kolejno dla ![]()
oraz ![]() .
.
Od razu nasuwają się dwie uwagi. Po pierwsze, iteracja odwrotna ma sens
tylko wtedy gdy parametr ![]() jest tak dobrany, że macierz
jest tak dobrany, że macierz ![]() jest nieosobliwa, co jest równoważne warunkowi
jest nieosobliwa, co jest równoważne warunkowi ![]() dla
wszystkich
dla
wszystkich ![]() . Po drugie, w realizacji numerycznej, dla znalezienia
wektora
. Po drugie, w realizacji numerycznej, dla znalezienia
wektora ![]() nie odwracamy macierzy
nie odwracamy macierzy ![]() , ale rozwiązujemy
układ równań
, ale rozwiązujemy
układ równań ![]() , co czyni metodę tak samo
kosztowną co iteracja prosta.
, co czyni metodę tak samo
kosztowną co iteracja prosta.
Analiza iteracji odwrotnych przebiega podobnie do analizy iteracji prostych
dla macierzy ![]() . Nietrudno zauważyć, że macierz ta ma
te same wektory własne co
. Nietrudno zauważyć, że macierz ta ma
te same wektory własne co ![]() , a jej wartości własne wynoszą
, a jej wartości własne wynoszą
(To wynika bezpośrednio z równości
![]() .)
Dlatego iteracje odwrotne zbiegają do wektora własnego odpowiadającego
wartości własnej
.)
Dlatego iteracje odwrotne zbiegają do wektora własnego odpowiadającego
wartości własnej ![]() takiej, że
takiej, że
przy czym szybkość zbieżności zależy teraz od wielkości
(a nie od ![]() , jak w iteracji prostej).
, jak w iteracji prostej).
Niewątpliwą zalety odwrotnej metody potęgowej jest to, że zbiega do
wartości własnej najbliższej ![]() , przy czym im
, przy czym im ![]() bliższe
bliższe
![]() tym lepiej. Metoda jest więc szczególnie efektywna w przypadku
gdy znamy dobre przybliżenia wartości własnych macierzy
tym lepiej. Metoda jest więc szczególnie efektywna w przypadku
gdy znamy dobre przybliżenia wartości własnych macierzy ![]() .
Niestety, taka informacja nie zawsze jest dana wprost.
.
Niestety, taka informacja nie zawsze jest dana wprost.
Pamiętając, że kolejne przybliżenia wartości własnej w metodzie potęgowej
są obliczane przy pomocy ilorazów Rayleigha, dobrym pomysłem na przesunięcie
wydaje się być wzięcie w ![]() -tym kroku iteracji odwrotnej
-tym kroku iteracji odwrotnej
Rzeczywiście. Niech ![]() będzie kątem pomiędzy
będzie kątem pomiędzy ![]() a podprzestrzenią własną
a podprzestrzenią własną ![]() . Zakładając, że
. Zakładając, że ![]() jest
dostatecznie blisko
jest
dostatecznie blisko ![]() oraz przyjmując
oraz przyjmując
![]() , na podstawie
twierdzenia 2.1 mamy
, na podstawie
twierdzenia 2.1 mamy
Zamiast zbieżności kwadratowej, jak w prostej metodzie potęgowej, dostaliśmy (asymptotycznie!) zbieżność sześcienną.
Metoda potęgowa, prosta lub odwrotna, pozwala wyznaczyć tylko jedną
wartość własną, powiedzmy ![]() , oraz odpowiadający jej wektor
własny. Naturalne jest teraz pytanie o to jak postępować, aby znaleźć
inne pary własne. Jednym ze sposobów jest zastosowanie deflacji.
, oraz odpowiadający jej wektor
własny. Naturalne jest teraz pytanie o to jak postępować, aby znaleźć
inne pary własne. Jednym ze sposobów jest zastosowanie deflacji.
Jeśli macierz jest hermitowska, ![]() , oraz znaleźliśmy wektor
własny
, oraz znaleźliśmy wektor
własny ![]() odpowiadający wartości własnej
odpowiadający wartości własnej ![]() , to
możemy ponowić proces metody potęgowej ograniczając go do podprzestrzeni
prostopadłej do
, to
możemy ponowić proces metody potęgowej ograniczając go do podprzestrzeni
prostopadłej do ![]() wymiaru
wymiaru ![]() . Osiągamy to startując z wektora
. Osiągamy to startując z wektora
![]() prostopadłego do
prostopadłego do ![]() , tzn.
, tzn.
gdzie ![]() jest wybrany losowo. Przy idealnej realizacji
procesu konstruowany ciąg
jest wybrany losowo. Przy idealnej realizacji
procesu konstruowany ciąg ![]() należałby do podprzestrzeni
prostopadłej do
należałby do podprzestrzeni
prostopadłej do ![]() . W obecności błędów zaokrągleń
należałoby to wymusić poprzez reortogonalizację,
. W obecności błędów zaokrągleń
należałoby to wymusić poprzez reortogonalizację,
wykonywaną np. co kilka kroków. Po znalezieniu drugiej pary własnej,
proces deflacji możemy kontynuować, ograniczając się do odpowiedniej
podprzestrzeni własnej wymiaru ![]() .
.




