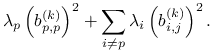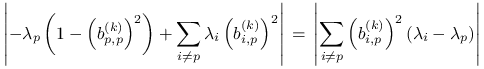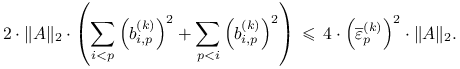Zagadnienia
3. Zagadnienie własne III
Metodę potęgową można traktować jako iteracje podprzestrzeni
jednowymiarowej startujące ze ![]() . Naturalnym
uogólnieniem tego procesu są iteracje podprzestrzeni o wyższych
wymiarach. Właśnie iteracje podprzestrzeni są punktem wyjścia
konstrukcji obecnie najpopularniejszego algorytmu QR, którego zadaniem
jest obliczenie jednocześnie wszystkich wartości własnych.
. Naturalnym
uogólnieniem tego procesu są iteracje podprzestrzeni o wyższych
wymiarach. Właśnie iteracje podprzestrzeni są punktem wyjścia
konstrukcji obecnie najpopularniejszego algorytmu QR, którego zadaniem
jest obliczenie jednocześnie wszystkich wartości własnych.
Chociaż metody prezentowane w tym rozdziale mogą być stosowane
w większej ogólności, dla uproszczenia będziemy zakładać, że
macierz ![]() jest nieosobliwa, rzeczywista i symetryczna,
tzn.
jest nieosobliwa, rzeczywista i symetryczna,
tzn. ![]() i
i ![]() . Przypomnijmy,
że wtedy istnieje baza ortonormalna
. Przypomnijmy,
że wtedy istnieje baza ortonormalna ![]() wektorów
własnych macierzy,
wektorów
własnych macierzy,
Będziemy również zakładać, że wartości własne są uporządkowane tak, że
3.1. Iteracje podprzestrzeni
3.1.1. Algorytm ogólny
Niech ![]() oraz
oraz ![]() będzie
podprzestrzenią o wymiarze
będzie
podprzestrzenią o wymiarze ![]() . Dla
. Dla ![]() rozpatrzmy
następujące iteracje:
rozpatrzmy
następujące iteracje:
Oczywiście, wobec nieosobliwości ![]() wszystkie podprzestrzenie
wszystkie podprzestrzenie ![]() mają też wymiar
mają też wymiar ![]() .
Pokażemy, że przy pewnych niekrępujących założeniach ciąg podprzestrzeni
.
Pokażemy, że przy pewnych niekrępujących założeniach ciąg podprzestrzeni
![]() zbiega do podprzestrzeni własnej
zbiega do podprzestrzeni własnej
przy czym przez ,,zbieżność” rozumiemy tu zbieżność do zera kąta pomiędzy tymi podprzestrzeniami.
Przypomnijmy, że kąt pomiędzy dwiema podprzestrzeniami
![]() definiujemy jako
definiujemy jako
(Jako ćwiczenie można wykazać, że jeśli
![]() to
to
![]() .)
.)
Twierdzenie 3.1
Niech
Jeśli ![]() to
to
Dowód
Niech ![]() będzie wektorem spełniającym
będzie wektorem spełniającym
![]() . Wtedy
. Wtedy
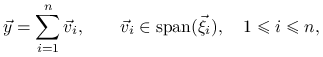 |
gdzie nie wszystkie ![]() dla
dla ![]() , są są zerowe, oraz
, są są zerowe, oraz
![]() . Stąd
. Stąd
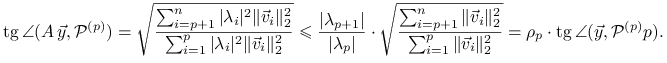 |
(3.1) |
Jeśli teraz ![]() dla
dla
![]() oraz
oraz ![]() to
z (3.1) wynika, że
to
z (3.1) wynika, że
co kończy dowód.
∎3.1.2. Iteracje ortogonalne
W praktyce, iteracje podprzestrzeni realizujemy reprezentując
kolejne ![]() przez ich bazy ortonormalne. Wtedy algorytm,
zwany w tym przypadku również iteracjami ortogonalnymi,
przybiera następującą postać.
Wybieramy macierz kolumnowo-ortogonalną
przez ich bazy ortonormalne. Wtedy algorytm,
zwany w tym przypadku również iteracjami ortogonalnymi,
przybiera następującą postać.
Wybieramy macierz kolumnowo-ortogonalną ![]() formatu
formatu ![]() jako
macierz startową, a następnie dla
jako
macierz startową, a następnie dla ![]() iterujemy:
iterujemy:
przy czym w drugiej linii następuje ortonormalizacja macierzy ![]() realizowana
poprzez rozkład tej macierzy na iloczyn macierzy kolumnowo-ortonormalnej
realizowana
poprzez rozkład tej macierzy na iloczyn macierzy kolumnowo-ortonormalnej ![]() formatu
formatu ![]() i macierzy trójkątnej górnej
i macierzy trójkątnej górnej ![]() formatu
formatu ![]() .
Dokonuje się tego znanym nam już algorytmem wykorzystującym odbicia Householdera.
.
Dokonuje się tego znanym nam już algorytmem wykorzystującym odbicia Householdera.
łatwo zauważyć, że jeśli przyjmiemy, iż wektory-kolumny macierzy ![]() tworzą bazę ortonormalną podprzestrzeni
tworzą bazę ortonormalną podprzestrzeni ![]() to w kolejnych krokach
wektory-kolumny
to w kolejnych krokach
wektory-kolumny ![]() tworzą bazę ortonormalną podprzestrzeni
tworzą bazę ortonormalną podprzestrzeni
![]() . Rzeczywiście, ponieważ
. Rzeczywiście, ponieważ ![]() to kolumny
to kolumny ![]() stanowią bazę
stanowią bazę ![]() . Kolumny te są z kolei liniową kombinacją
kolumn
. Kolumny te są z kolei liniową kombinacją
kolumn ![]() , czyli rozpinają tą samą podprzestrzeń co kolumny
, czyli rozpinają tą samą podprzestrzeń co kolumny ![]() .
.
Poczynimy teraz kluczową obserwację. Przypuśćmy, że wszystkie wartości
własne ![]() są parami różne. Gdybyśmy rozpoczynali iteracje
od macierzy
są parami różne. Gdybyśmy rozpoczynali iteracje
od macierzy ![]() składającej się jedynie z
składającej się jedynie z ![]() początkowych kolumn macierzy
początkowych kolumn macierzy ![]() , przy czym
, przy czym ![]() , to otrzymane
w procesie iteracyjnym macierze
, to otrzymane
w procesie iteracyjnym macierze ![]() i
i ![]() (formatu
(formatu
![]() i
i ![]() ) byłyby odpowiednio
,,okrojonymi” macierzami
) byłyby odpowiednio
,,okrojonymi” macierzami ![]() i
i ![]() . Stąd, jeśli wszystkie wartości własne
macierzy
. Stąd, jeśli wszystkie wartości własne
macierzy ![]() mają różne moduły, to dla każdego takiego
mają różne moduły, to dla każdego takiego ![]() podprzestrzeń
podprzestrzeń ![]() rozpięta na początkowych
rozpięta na początkowych
![]() wektorach macierzy
wektorach macierzy ![]() ,,zbiega” do podprzestrzeni własnej
,,zbiega” do podprzestrzeni własnej
![]() , przy czym
, przy czym
Z powyższej obserwacji wynika, że gdybyśmy realizowali iteracje
podprzestrzeni przyjmując ![]() i startując z macierzy identycznościowej
i startując z macierzy identycznościowej
![]() formatu
formatu ![]() to mielibyśmy zbieżność
to mielibyśmy zbieżność ![]() do podprzestrzeni własnych
do podprzestrzeni własnych ![]() dla wszystkich
dla wszystkich ![]() .
.
W przypadku gdy pracujemy na bazach ortogonalnych i startujemy z ![]() ,
zbieżność tą można wyrazić również w następujący sposób. Oznaczmy
,
zbieżność tą można wyrazić również w następujący sposób. Oznaczmy
Lemat 3.1
Niech ![]() będzie macierzą przejścia od bazy
będzie macierzą przejścia od bazy ![]() do
do ![]() ,
,
Dla ![]() , niech
, niech
![B_{k}=\left[\begin{array}[]{cc}B_{{1,1}}^{{(k)}}&B_{{1,2}}^{{(k)}}\\
B_{{2,1}}^{{(k)}}&B_{{2,2}}^{{(k)}}\end{array}\right],](wyklady/mo2/mi/mi517.png) |
gdzie ![]() jest podmacierzą formatu
jest podmacierzą formatu ![]() , a pozostałe
podmacierze odpowiednio formatów
, a pozostałe
podmacierze odpowiednio formatów ![]() ,
, ![]() ,
,
![]() . Jeśli
. Jeśli ![]() i
i ![]() to
to
Dowód
Niech ![]() ,
, ![]() , gdzie
, gdzie ![]() i
i ![]() są formatu
są formatu ![]() . Wtedy
. Wtedy
Mnożąc to równanie z lewej strony przez ![]() dostajemy
dostajemy
![]() . Stąd
. Stąd
Oznaczając ![]() zauważamy, że
zauważamy, że
![]() i
i ![]() . Stąd wektor
. Stąd wektor ![]() zawiera współczynniki
rzutu ortogonalnego
zawiera współczynniki
rzutu ortogonalnego ![]() na
na
![]() w bazie
w bazie ![]() . Z definicji normy drugiej
i twierdzenia 3.1 dostajemy więc
. Z definicji normy drugiej
i twierdzenia 3.1 dostajemy więc
Rozumując analogicznie i wykorzystując fakt, że
dostajemy taką samą nierówność dla ![]() .
.
Z lematu 3.1 wynika natychmiast, że jeśli moduły wartości
własnych macierzy ![]() są parami różne to wyrazy pozadiagonalne
są parami różne to wyrazy pozadiagonalne
![]() macierzy
macierzy ![]() zbiegają do zera, a ponieważ
zbiegają do zera, a ponieważ ![]() jest
ortogonalna, to
jest
ortogonalna, to ![]() zbiegają do jedynki. Algorytm (IO)
można więc uzupełnić o obliczanie w każdym kroku macierzy
zbiegają do jedynki. Algorytm (IO)
można więc uzupełnić o obliczanie w każdym kroku macierzy
która powinna zbiegać do
![]() .
Fakt ten, łącznie z analizą szybkości zbieżności, pokażemy
formalnie w następnym podrozdziale.
.
Fakt ten, łącznie z analizą szybkości zbieżności, pokażemy
formalnie w następnym podrozdziale.
3.2. Metoda QR
3.2.1. Wyprowadzenie metody
Załóżmy, że realizujemy algorytm iteracji ortogonalnych (IO) z macierzą
początkową ![]() . Wtedy
. Wtedy ![]() , skąd
, skąd
Oznaczając ![]() widzimy, że ostatnia równość to nic innego jak
rozkład ortogonalno-trójkątny macierzy
widzimy, że ostatnia równość to nic innego jak
rozkład ortogonalno-trójkątny macierzy ![]() ,
,
Prawdziwe są więc związki rekurencyjne
Zależności te prowadzą do ALGORYTMU QR, który oblicza
kolejne macierze ![]() i
i ![]() w następujący sposób.
w następujący sposób.
| (QR) |
3.2.2. QR a iteracje ortogonalne
Przypomnijmy, że w rozkładzie ortogonalno-trójkątnym macierz
ortogonalna jest wyznaczona jednoznacznie z dokładnością do znaków
jej wektorów-kolumn. Dlatego macierze ![]() (a tym samym także
(a tym samym także ![]() )
powstałe w wyniku realizacji algorytmów (IO) i (QR) nie muszą być
takie same. Algorytmy te są jednak równoważne w następującym sensie.
)
powstałe w wyniku realizacji algorytmów (IO) i (QR) nie muszą być
takie same. Algorytmy te są jednak równoważne w następującym sensie.
Lemat 3.2
Niech ![]() ,
, ![]() i
i ![]() ,
, ![]() będą macierzami
powstałymi w wyniku realizacji odpowiednio algorytmów (IO) i (QR). Wtedy
będą macierzami
powstałymi w wyniku realizacji odpowiednio algorytmów (IO) i (QR). Wtedy
gdzie ![]() są pewnymi macierzami diagonalnymi z elementami
są pewnymi macierzami diagonalnymi z elementami ![]() na głównej przekątnej.
na głównej przekątnej.
Dowód
Zastosujemy indukcję względem ![]() . Dla
. Dla ![]() mamy
mamy
![]() oraz
oraz ![]() .
Załóżmy, że lemat jest prawdziwy dla
.
Załóżmy, że lemat jest prawdziwy dla ![]() , tzn.
, tzn.
![]() . Wtedy, z jednej strony
. Wtedy, z jednej strony
a z drugiej strony
Mamy więc
przy czym równości te przedstawiają dwa rozkłady ortogonalno-trójkątne
tej samej macierzy ![]() . A jeśli tak, to czynniki
ortogonalne tych rozkładów różnią się jedynie znakami kolumn.
Równoważnie, istnieje macierz diagonalna
. A jeśli tak, to czynniki
ortogonalne tych rozkładów różnią się jedynie znakami kolumn.
Równoważnie, istnieje macierz diagonalna ![]() z elementami
z elementami ![]() na głównej
przekątnej taka, że
na głównej
przekątnej taka, że
Stąd
Dowód kończy następujący rachunek:
Zauważmy jeszcze, że jeśli przez ![]() i
i ![]() oznaczymy odpowiednio elementy macierzy
oznaczymy odpowiednio elementy macierzy ![]() i
i ![]() oraz
oraz
![]() z
z ![]() to
to
To oznacza, że dla ![]() elementy te różnią się jedynie znakiem,
a dla
elementy te różnią się jedynie znakiem,
a dla ![]() są sobie równe.
są sobie równe.
3.2.3. Analiza zbieżności
Jesteśmy już gotowi do przedstawienia twierdzeń o zbieżności metody QR.
Twierdzenie 3.2
Dla ![]() , niech
, niech ![]() i
i
![]() .
Niech dalej
.
Niech dalej
![A_{k}=\left[\begin{array}[]{cc}A_{{1,1}}^{{(k)}}&A_{{1,2}}^{{(k)}}\\
A_{{2,1}}^{{(k)}}&A_{{2,2}}^{{(k)}}\end{array}\right],\quad Q_{k}=\left[\begin{array}[]{cc}Q_{{1,1}}^{{(k)}}&Q_{{1,2}}^{{(k)}}\\
Q_{{2,1}}^{{(k)}}&Q_{{2,2}}^{{(k)}}\end{array}\right],\quad R_{k}=\left[\begin{array}[]{cc}R_{{1,1}}^{{(k)}}&R_{{1,2}}^{{(k)}}\\
0&R_{{2,2}}^{{(k)}}\end{array}\right],](wyklady/mo2/mi/mi425.png) |
gdzie podmacierze ![]() są
formatu
są
formatu ![]() , a pozostałe podmacierze formatów odpowiednio
, a pozostałe podmacierze formatów odpowiednio
![]() ,
, ![]() i
i ![]() . Wtedy,
przyjmując
. Wtedy,
przyjmując
mamy ![]() \tg oraz
\tg oraz
| (3.2) | |||||
| (3.3) | |||||
| (3.4) |
Dowód
Wobec wykazanej w lemacie \tg (teoretycznej) równoważności metody
QR i iteracji (IO), nierówność ![]() została
już udowodniona w twierdzeniu 3.1. Aby pokazać (3.3),
zapiszemy
została
już udowodniona w twierdzeniu 3.1. Aby pokazać (3.3),
zapiszemy ![]() w postaci
w postaci ![]() , gdzie
, gdzie ![]() i
i ![]() składają się odpowiednio z pierwszych
składają się odpowiednio z pierwszych ![]() i z ostatnich
i z ostatnich ![]() kolumn
macierzy
kolumn
macierzy ![]() . Wtedy
. Wtedy
gdzie ![]() . Pisząc
. Pisząc ![]() ,
podobnie jak dla
,
podobnie jak dla ![]() , mamy teraz
, mamy teraz
![V^{T}\, Z_{1}^{{(k)}}=\left[\begin{array}[]{cc}V_{1}^{T}\, Z_{1}^{{(k)}}\\
V_{2}^{T}\, Z_{1}^{{(k)}}\end{array}\right]=:\left[\begin{array}[]{cc}F\\
G\end{array}\right].](wyklady/mo2/mi/mi596.png) |
Ponieważ ![]() to
to ![]() , natomiast
, natomiast
![]() , jak pokazaliśmy w dowodzie
lematu 3.1.
, jak pokazaliśmy w dowodzie
lematu 3.1.
Pisząc z kolei
w analogiczny sposób pokazujemy, że
![]() i
i ![]() . Stąd mamy
. Stąd mamy
Dokładnie tak samo pokazujemy oszacowanie dla ![]() .
.
Aby pokazać (3.2) zauważmy, że wobec ![]() mamy też
mamy też
![]() . Ale
. Ale
co w połączeniu z (3.3) dowodzi (3.2).
W końcu, wobec ![]() mamy
mamy
Nierówność (3.4) wynika teraz z nierówności
![]() , (3.2), (3.3),
oraz
, (3.2), (3.3),
oraz ![]() .
.
Z twierdzenia 3.2 wynika, że elementy pozadiagonalne
macierzy ![]() zbiegają do zera liniowo, przy czym iloraz zbieżności
zależy od wartości
zbiegają do zera liniowo, przy czym iloraz zbieżności
zależy od wartości ![]() . Dokładniej,
dla danego elementu
. Dokładniej,
dla danego elementu ![]() macierzy
macierzy ![]() , gdzie
, gdzie ![]() ,
prawdziwe jest oszacowanie
,
prawdziwe jest oszacowanie
(gdzie skorzystaliśmy także z faktu, że moduł pojedynczego elementu macierzy jest nie większy od normy drugiej tej macierzy).
A jaka jest zbieżność elementów diagonalnych ![]() do wartości własnych
macierzy
do wartości własnych
macierzy ![]() ? Oznaczmy
? Oznaczmy
![\overline{\varepsilon}_{p}^{{(k)}}=\left\{\begin{array}[]{ll}\varepsilon _{1}^{{(k)}}&p=1,\\
\max\left(\varepsilon _{{p-1}}^{{(k)}},\varepsilon _{p}^{{(k)}}\right)&2\le p\le n-1,\\
\varepsilon _{{n-1}}^{{(k)}}&p=n.\end{array}\right.](wyklady/mo2/mi/mi593.png) |
Twierdzenie 3.3
Dla wszystkich ![]() mamy
mamy
Elementy diagonalne ![]() macierzy
macierzy ![]() zbiegają więc do
wartości własnych
zbiegają więc do
wartości własnych ![]() macierzy
macierzy ![]() co najmniej jak
co najmniej jak
![]() dla
dla ![]() ,
, ![]() dla
dla ![]() ,
oraz
,
oraz ![]() dla
dla ![]() .
.
3.3. QR z przesunięciami i deflacja
Tak jak w przypadku metody potęgowej, można spróbować przyspieszyć zbieżność
metody QR poprzez przesunięcie widma macierzy ![]() , czyli zastosowanie QR do macierzy
, czyli zastosowanie QR do macierzy
![]() . Oznaczmy przez
. Oznaczmy przez ![]() kolejne macierze powstające
w tym procesie. Z wcześniejszej analizy metody QR wynika, że jeśli
kolejne macierze powstające
w tym procesie. Z wcześniejszej analizy metody QR wynika, że jeśli
to wyraz ![]() w prawym dolnym rogu macierzy
w prawym dolnym rogu macierzy
![]() zbiega do
zbiega do ![]() i zbieżność jest tym lepsza
im
i zbieżność jest tym lepsza
im ![]() jest bliższe
jest bliższe ![]() . Dlatego ważne jest, aby
. Dlatego ważne jest, aby ![]() wybrać tak, aby dobrze aproksymowała jedną z wartości własnych macierzy
wybrać tak, aby dobrze aproksymowała jedną z wartości własnych macierzy ![]() .
Oczywiście, przesunięcie możnaby w każdym kroku wybierać w zależności
od aktualnie dostępnej informacji. Metoda wyglądałaby wtedy następująco:
.
Oczywiście, przesunięcie możnaby w każdym kroku wybierać w zależności
od aktualnie dostępnej informacji. Metoda wyglądałaby wtedy następująco:
| (QR-shift) |
Jasne, że
tzn. kolejne macierze ![]() są ortogonalnie podobne. Okazuje się, że
QR ma jeszcze jedną ważną własność.
Oznaczmy przez
są ortogonalnie podobne. Okazuje się, że
QR ma jeszcze jedną ważną własność.
Oznaczmy przez ![]() ostatnią kolumnę macierzy
ostatnią kolumnę macierzy ![]() , przez
, przez
![]() wyraz w prawym dolnym rogu macierzy trójkątnej górnej
wyraz w prawym dolnym rogu macierzy trójkątnej górnej
![]() , oraz przez
, oraz przez ![]() ostatni wersor. Wtedy dla każdego
ostatni wersor. Wtedy dla każdego ![]() mamy
mamy
czyli
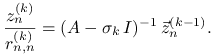 |
To zaś oznacza, że w kolejnych krokach iteracji QR z przesunięciami ![]() ostatnia kolumna macierzy
ostatnia kolumna macierzy ![]() jest taka sama jak wektor
jest taka sama jak wektor ![]() w odwrotnej
metodzie potęgowej z wektorem startowym
w odwrotnej
metodzie potęgowej z wektorem startowym ![]() i kolejnymi przesunięciami
i kolejnymi przesunięciami
![]() . A jeśli tak, to możemy wykorzystać wyniki rozdziału 2.4
i stwierdzić, że dobrym wyborem przesunięcia jest
. A jeśli tak, to możemy wykorzystać wyniki rozdziału 2.4
i stwierdzić, że dobrym wyborem przesunięcia jest
Przy tak dobranym ![]() dostajemy asymptotycznie zbieżność sześcienną
elementu
dostajemy asymptotycznie zbieżność sześcienną
elementu ![]() do
do ![]() .
.
Dla informacji podamy jeszcze, że możliwy jest też wybór
przesunięcia Wilkinsona, gdzie jako ![]() bierze się tą
wartość własną macierzy
bierze się tą
wartość własną macierzy ![]() ,
,
![\left[\begin{array}[]{ll}a_{{n-1,n-1}}^{{(k)}}&a_{{n-1,n}}^{{(k)}}\\
a_{{n,n-1}}^{{(k)}}&a_{{n,n}}^{{(k)}}\end{array}\right],](wyklady/mo2/mi/mi416.png) |
która jest najbliższa ![]() , a jeśli obie są jednakowo oddalone
od
, a jeśli obie są jednakowo oddalone
od ![]() to mniejszą z nich. Wtedy co prawda nie zwiększamy szybkości
zbieżności, ale za to metoda jest zawsze zbieżna.
to mniejszą z nich. Wtedy co prawda nie zwiększamy szybkości
zbieżności, ale za to metoda jest zawsze zbieżna.
Pozostałe wartości własne macierzy ![]() możemy obliczyć stosując deflację.
Mianowicie, gdy już jesteśmy dostatecznie blisko wartości własnej
możemy obliczyć stosując deflację.
Mianowicie, gdy już jesteśmy dostatecznie blisko wartości własnej ![]() (co zwykle osiąga się wykonując kilka kroków QR i sprawdza przez obliczenie
residuum
(co zwykle osiąga się wykonując kilka kroków QR i sprawdza przez obliczenie
residuum ![]() ) to uznajemy, że
wyrazy w ostatniej kolumnie i ostatnim wierszu macierzy
) to uznajemy, że
wyrazy w ostatniej kolumnie i ostatnim wierszu macierzy ![]() , poza wyrazem
, poza wyrazem
![]() , są zerowe i redukujemy problem do macierzy formatu
, są zerowe i redukujemy problem do macierzy formatu ![]() .
Oczywiście, ten ogólny przepis wymaga właściwej implementacji.
.
Oczywiście, ten ogólny przepis wymaga właściwej implementacji.