Zagadnienia
4. Zagadnienie własne IV
W tym rozdziale zajmiemy się jeszcze innymi nich dotychczas poznanymi metodami znajdowania wartości i wektorów własnych. Ponieważ duże znaczenie mają w nich obroty płaszczyzn, zaczniemy właśnie od definicji tych przekształceń, ich własności i pierwszych zastosowań.
4.1. Obroty Givensa
4.1.1. Definicja obrotu
Macierz obrotu o kąt ![]() w płaszczyźnie rozpiętej na
wersorach
w płaszczyźnie rozpiętej na
wersorach ![]() , gdze
, gdze ![]() , jest postaci
, jest postaci
![O_{{i,j}}=\left[\begin{array}[]{ccccccccccc}1\\
&\ddots\\
&&\cos\varphi&&\sin\varphi\\
&&&\ddots\\
&&-\sin\varphi&&\cos\varphi\\
&&&&&\ddots\\
&&&&&&1\end{array}\right].](wyklady/mo2/mi/mi808.png) |
Macierz ta różni się od jednostkowej jedynie wyrazami
![]() oraz
oraz ![]() .
łatwo sprawdzić, że
.
łatwo sprawdzić, że ![]() jest przekształceniem
ortogonalnym,
jest przekształceniem
ortogonalnym, ![]()
W obliczeniach numerycznych macierze obrotu służą najczęściej
do wyzerowania określonej współrzędnej danego wektora.
Rzeczywiście, obracając wektor ![]() w płaszczyźnie rozpiętej na
w płaszczyźnie rozpiętej na ![]() i
i ![]() zmieniamy
jedynie współrzędne
zmieniamy
jedynie współrzędne ![]() -tą i
-tą i ![]() -tą. Dokładniej,
-tą. Dokładniej,
![]() , gdzie
, gdzie
![b_{k}=\left\{\begin{array}[]{rl}a_{i}\cos\varphi+a_{j}\sin\varphi,&k=i,\\
-a_{i}\sin\varphi+a_{j}\cos\varphi,&k=j,\\
a_{k},&k\ne i,j.\end{array}\right.](wyklady/mo2/mi/mi856.png) |
Stąd, przyjmując
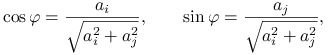 |
albo liczby do nich przeciwne, dostajemy ![]() albo
albo ![]() , oraz
, oraz ![]() . Z powyższych wzorów
wynika, że kąt obrotu
. Z powyższych wzorów
wynika, że kąt obrotu ![]() można zawsze
tak dobrać, aby
można zawsze
tak dobrać, aby ![]() .
.
Przekształcenia tak określone nazywamy obrotami Givensa.
Zauważmy, że stosując obroty Givensa kolejno
w płaszczyznach rozpiętych na wektorach
![]() i
i ![]() dla
dla ![]() możemy
przekształcić dany wektor
możemy
przekształcić dany wektor ![]() na kierunek pierwszego
wersora, tzn.
na kierunek pierwszego
wersora, tzn.
Takie operacje wymagają wykonania ![]() mnożeń/dodawań i
mnożeń/dodawań i ![]() pierwiastkowań. Przypomnijmy, że ten sam efekt można uzyskać
kosztem około
pierwiastkowań. Przypomnijmy, że ten sam efekt można uzyskać
kosztem około ![]() mnożeń/dodawań i jednego pierwiastka stosując
odbicia Householdera. Wydaje się więc, że obroty Givensa opłaca się
stosować jedynie wtedy, gdy wektor
mnożeń/dodawań i jednego pierwiastka stosując
odbicia Householdera. Wydaje się więc, że obroty Givensa opłaca się
stosować jedynie wtedy, gdy wektor ![]() ma niewiele (proporcjonalnie
do
ma niewiele (proporcjonalnie
do ![]() ) współrzędnych niezerowych. Nie jest to jednak do końca prawdą.
Istnieje bowiem pewna modyfikacja podanych wzorów autorstwa Gentlemana
pozwalająca istotnie zmniejszyć koszt, którą teraz zaprezentujemy.
) współrzędnych niezerowych. Nie jest to jednak do końca prawdą.
Istnieje bowiem pewna modyfikacja podanych wzorów autorstwa Gentlemana
pozwalająca istotnie zmniejszyć koszt, którą teraz zaprezentujemy.
4.1.2. Algorytm Gentlemana
Przypuśćmy, że chcemy zastosować serię obrotów Givensa ![]() dla
dla ![]() , gdzie
, gdzie ![]() -ty obrót jest wybrany tak, że
-ty obrót jest wybrany tak, że
![]() -ta współrzędna wektora
-ta współrzędna wektora
jest zerowa. Pomysł modyfikacji polega na przedstawieniu każdego z obrotów w postaci
gdzie ![]() , a
, a ![]() są pewnymi nieosobliwymi macierzami diagonalnymi
wybranymi tak, by mnożenie przez
są pewnymi nieosobliwymi macierzami diagonalnymi
wybranymi tak, by mnożenie przez ![]() było prostsze niż
mnożenie przez
było prostsze niż
mnożenie przez ![]() . Wtedy mamy
. Wtedy mamy
Macierze diagonalne ![]() ,
a tym samym i przekształcenia
,
a tym samym i przekształcenia ![]() , zdefiniujemy indukcyjnie
dla
, zdefiniujemy indukcyjnie
dla ![]() . Załóżmy, że zdefiniowaliśmy już
. Załóżmy, że zdefiniowaliśmy już
![]() . Niech
. Niech ![]() będzie obrotem
o kąt
będzie obrotem
o kąt ![]() oraz
oraz ![]() ,
, ![]() .
.
Dla uproszczenia zapisu podstawimy ![]() ,
,
![]() oraz
oraz
![]() ,
, ![]() . Dalej mamy
. Dalej mamy ![]() ,
,
![]() . Ponieważ
. Ponieważ
![]() to
to
![s_{{i,j}}\,=\,\frac{d_{j}}{\hat{d}_{i}}\, o_{{i,j}}\,=\,\left\{\begin{array}[]{rl}cd_{{p}}/\hat{d}_{{p}},&i=j=p,\\
cd_{{q}}/\hat{d}_{{q}},&i=j=q,\\
sd_{{q}}/\hat{d}_{{p}},&i=p,j=q,\\
-sd_{{p}}/\hat{d}_{{q}},&i=q,j=p,\\
d_{j}/\hat{d}_{i},&i=j\ne p,q,\\
0,&\mbox{wpp}.\end{array}\right.](wyklady/mo2/mi/mi824.png) |
Przypomnijmy, że obrót ![]() jest wybrany tak, że
jest wybrany tak, że
![]() . Zauważmy, że dla
. Zauważmy, że dla
mamy
Stąd warunek ![]() jest równoważny warunkowi
jest równoważny warunkowi
![]() , czyli
, czyli
Jeśli teraz ![]() to przyjmujemy
to przyjmujemy
![]() i
i ![]() . W przeciwnym przypadku,
uwzględniając równość
. W przeciwnym przypadku,
uwzględniając równość ![]() , dostajemy
, dostajemy
 |
Mamy teraz dwa przypadki.
(i) Jeśli ![]() to kładziemy
to kładziemy
![]() ,
, ![]() i
i ![]() dla
dla ![]() . Wtedy
. Wtedy ![]() dla
dla ![]() oraz
oraz
gdzie
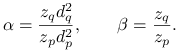 |
(ii) Jeśli ![]() to kładziemy
to kładziemy
![]() ,
, ![]() i
i ![]() dla
dla ![]() . Wtedy
. Wtedy ![]() dla
dla ![]() oraz
oraz
gdzie
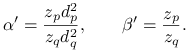 |
Macierz ![]() ma podobną strukturę jak
ma podobną strukturę jak ![]() .
Obecność dwóch jedynek pozwalaja jednak zaoszczędzić dwa mnożenia
przy operacji
.
Obecność dwóch jedynek pozwalaja jednak zaoszczędzić dwa mnożenia
przy operacji ![]() w porównaniu do
w porównaniu do ![]() .
Ponadto, co jest ważniejsze, obliczanie wielkości
.
Ponadto, co jest ważniejsze, obliczanie wielkości ![]() i
i ![]() (ew.
(ew. ![]() i
i ![]() ) definiujących
) definiujących ![]() nie wymaga
pierwiastkowania. Rzeczywiście, w kolejnych krokach procesu obliczeniowego
wystarczy pamiętać współczynniki
nie wymaga
pierwiastkowania. Rzeczywiście, w kolejnych krokach procesu obliczeniowego
wystarczy pamiętać współczynniki ![]() . Współczynniki te
wyliczane są rekurencyjnie zgodnie ze wzorami
. Współczynniki te
wyliczane są rekurencyjnie zgodnie ze wzorami ![]() dla
dla
![]() , a dla
, a dla ![]()
Zauważmy, jeszcze, że takie rozbicie na przypadki (i) i (ii) pozwala
nie tylko uniknąć dzielenia przez zero, ale również uniknąć
możliwego niedomiaru. Wielkość ![]() jeśli zachodzi (i) oraz
jeśli zachodzi (i) oraz ![]() jeśli zachodzi (ii) jest w przedziale
jeśli zachodzi (ii) jest w przedziale ![]() .
.
Możnaby się spytać gdzie jest zysk obliczeniowy. Na końcu procesu
dysponujemy bowiem jedynie macierzą ![]() i aby pomnożyć przez
i aby pomnożyć przez ![]() należy najpierw wykonać
należy najpierw wykonać ![]() pierwiastkowań. Nie jest to jednak zawsze prawdą.
pierwiastkowań. Nie jest to jednak zawsze prawdą.
Na przykład, jeśli chcemy przekształcić dany wektor ![]() na
kierunek wersora
na
kierunek wersora ![]() przy pomocy obrotów Givensa to po wykonaniu serii
przy pomocy obrotów Givensa to po wykonaniu serii
![]() przekształceń
przekształceń
jedynie pierwsza współrzędna otrzymanego wektora nie jest zerowa.
Mnożenie przez ![]() sprowadza się więc do operacji na jego pierwszej
współrzędnej, to zaś wymaga obliczenia tylko jednego pierwiastka kwadratowego.
sprowadza się więc do operacji na jego pierwszej
współrzędnej, to zaś wymaga obliczenia tylko jednego pierwiastka kwadratowego.
Podobnie, używając obrotów Givensa można kosztem porównywalnym do
algorytmu bazującego na odbiciach Householdera przekształcić daną
nieosobliwą macierz kwadratową ![]() do postaci trójkątnej górnej
(albo, równoważnie, znaleźć jej rozkład ortogonalno-trójkątny).
Rzeczywiście, dokonuje się tego wykonując najpierw na macierzy serię
do postaci trójkątnej górnej
(albo, równoważnie, znaleźć jej rozkład ortogonalno-trójkątny).
Rzeczywiście, dokonuje się tego wykonując najpierw na macierzy serię
![]() przekształceń
przekształceń
gdzie ![]() jest tak dobrana, aby wyzerować współrzędną
jest tak dobrana, aby wyzerować współrzędną ![]() aktualnej macierzy, a następnie mnożąc kolejne wiersze otrzymanej
macierzy trójkątnej górnej przez pierwiastki z kolejnych elementów
diagonalnych macierzy
aktualnej macierzy, a następnie mnożąc kolejne wiersze otrzymanej
macierzy trójkątnej górnej przez pierwiastki z kolejnych elementów
diagonalnych macierzy ![]() . Całość wymaga więc obliczenia
. Całość wymaga więc obliczenia ![]() pierwiastków kwadratowych, podobnie jak w algorytmie Householdera.
(Należy przy tym pamiętać, aby nie wykonywać niepotrzebnie operacji
na elementach zerowych!)
pierwiastków kwadratowych, podobnie jak w algorytmie Householdera.
(Należy przy tym pamiętać, aby nie wykonywać niepotrzebnie operacji
na elementach zerowych!)
4.2. Metoda Jacobiego
Metoda Jacobiego jest najstarszą z istniejących metod numerycznych znajdowania wartości własnych macierzy symetrycznych. Ma jednak nie tylko znaczenie historyczne. Chociaż jest stosunkowo wolno zbieżna to można ją stosować gdy chcemy obliczyć wartości własne z bardzo dobrą dokładnością w obecności błędów zaokrągleń.
Zakładamy, że ![]() jest macierzą symetryczną. Podobnie
jak w metodzie QR, metoda Jacobiego startuje z macierzy
jest macierzą symetryczną. Podobnie
jak w metodzie QR, metoda Jacobiego startuje z macierzy ![]() i
produkuje ciąg macierzy podobnych
i
produkuje ciąg macierzy podobnych ![]() dla
dla ![]() , który
zbiega do macierzy diagonalnej
, który
zbiega do macierzy diagonalnej
składającej się z wartości własnych ![]() . Różnica polega na tym, że
pojedyncze kroki metody wykonuje się używając obrotów Givensa,
. Różnica polega na tym, że
pojedyncze kroki metody wykonuje się używając obrotów Givensa,
Oznaczając ![]() mamy więc
mamy więc ![]() .
.
Jako miarę odchylenia od macierzy diagonalnej ![]() w naturalny
sposób przyjmiemy połowę sumy kwadratów elementów pozadiagonalnych, czyli
w naturalny
sposób przyjmiemy połowę sumy kwadratów elementów pozadiagonalnych, czyli
gdzie ![]() . Wielkość
. Wielkość ![]() dobrze charakteryzuje
również błąd przybliżenia wartości własnych macierzy
dobrze charakteryzuje
również błąd przybliżenia wartości własnych macierzy ![]() przez elementy
diagonalne macierzy
przez elementy
diagonalne macierzy ![]() . Rzeczywiście, niech
. Rzeczywiście, niech
i ![]() . Wtedy
. Wtedy
gdzie ![]() oraz
oraz
Wyrazy diagonalne macierzy ![]() są więc wartościami własnymi macierzy
są więc wartościami własnymi macierzy
![]() , którą możemy potraktować jako zaburzoną macierz
, którą możemy potraktować jako zaburzoną macierz ![]() . Korzystając
z twierdzenia Weyla 1.3 dostajemy, że istnieje takie uporządkowanie
. Korzystając
z twierdzenia Weyla 1.3 dostajemy, że istnieje takie uporządkowanie
![]() wartości własnych macierzy
wartości własnych macierzy ![]() , że
dla wszystkich
, że
dla wszystkich ![]() mamy
mamy
Stąd wniosek, że poszczególne obroty ![]() powinniśmy wybierać tak,
aby maksymalizować różnicę
powinniśmy wybierać tak,
aby maksymalizować różnicę ![]() . Aby odpowiedzieć na
pytanie który obrót osiąga ten cel, przeanalizujmy pojedynczy krok. Dla
prostoty zapisu oznaczymy
. Aby odpowiedzieć na
pytanie który obrót osiąga ten cel, przeanalizujmy pojedynczy krok. Dla
prostoty zapisu oznaczymy ![]() ,
, ![]() ,
, ![]() ,
,
![]() , gdzie
, gdzie ![]() jest obrotem o kąt
jest obrotem o kąt ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Zauważmy, że mnożenie z lewej strony przez obrót ![]() zmienia jedynie
wiersze
zmienia jedynie
wiersze ![]() -ty i
-ty i ![]() -ty macierzy, a mnożenie z prawej strony przez
-ty macierzy, a mnożenie z prawej strony przez ![]() zmienia kolumny
zmienia kolumny ![]() -tą i
-tą i ![]() -tą. Dlatego dla
-tą. Dlatego dla ![]() i
i ![]() wyrazy
wyrazy
![]() i
i ![]() są sobie równe. Jeśli zaś
są sobie równe. Jeśli zaś ![]() i
i ![]() to
to
a stąd
i podobnie ![]() .
Otrzymujemy
.
Otrzymujemy
Dla danych ![]() wielkości
wielkości ![]() i
i ![]() definiujące obrót należy więc
wybrać tak, aby
definiujące obrót należy więc
wybrać tak, aby
Jeśli ![]() to powyższą równość realizuje obrót zerowy.
Załóżmy więc, że
to powyższą równość realizuje obrót zerowy.
Załóżmy więc, że ![]() . Bezpośredni rachunek pokazuje,
że wtedy
. Bezpośredni rachunek pokazuje,
że wtedy
Stąd równość ![]() zachodzi wtedy gdy
zachodzi wtedy gdy
Jeśli podstawimy ![]() \tg to ostatnia równość jest
równoważna równaniu kwadratowemu
\tg to ostatnia równość jest
równoważna równaniu kwadratowemu
Rozwiązując otrzymujemy następujące wzory:
Zauważmy jeszcze, że taka postać rozwiązania pozwala obliczyć
![]() i
i ![]() z małym błędem względnym w arytmetyce maszyny cyfrowej.
z małym błędem względnym w arytmetyce maszyny cyfrowej.
Pozostaje do ustalenia jak wybierać kolejne ![]() .
W oryginalnej wersji algorytmu
.
W oryginalnej wersji algorytmu ![]() wybierane są tak, że
wybierane są tak, że
Ponieważ wtedy ![]() , gdzie
, gdzie ![]() to
to
| (4.1) |
Mamy więc zapewnioną zbieżność liniową, chociaż iloraz
zbieżności jest bliski jedynce dla dużych wymiarów ![]() .
Taki wybór jest jednak zbyt kosztowny, bo wymaga znalezienia
w każdym kroku elementu największego co do modułu wśród
.
Taki wybór jest jednak zbyt kosztowny, bo wymaga znalezienia
w każdym kroku elementu największego co do modułu wśród
![]() elementów. Dlatego stosowane są inne strategie. Na przykład,
elementów. Dlatego stosowane są inne strategie. Na przykład,
i dalej cyklicznie, aż do osiągnięcia żądanej dokładności.
W tym przypadku kłopot polega na tym, że obroty wykonuje się
również wtedy, gdy ![]() jest znacznie mniejsze od
jest znacznie mniejsze od
![]() , co nie jest opłacalne. Aby temu zapobiec, można
wprowadzić pewien próg
, co nie jest opłacalne. Aby temu zapobiec, można
wprowadzić pewien próg ![]() i nie wykonywać obrotów gdy
i nie wykonywać obrotów gdy
![]() . Na przykład, możemy wziąć
. Na przykład, możemy wziąć
![]() . Wtedy, po wykonaniu każdego kroku
spełniona jest nierówność (4.1).
. Wtedy, po wykonaniu każdego kroku
spełniona jest nierówność (4.1).
4.3. QR dla macierzy trójdiagonalnej
Metodę Jacobiego stosuje się do pełnej, rzeczywistej macierzy
symetrycznej. W tym podrozdziale zatrzymamy się na przypadku, gdzie
![]() jest dodatkowo trójdiagonalna,
jest dodatkowo trójdiagonalna,
![A=T=\left[\begin{array}[]{cccc}a_{1}&b_{1}&&\\
b_{1}&\ddots&\ddots&\\
&\ddots&\ddots&b_{{n-1}}\\
&&b_{{n-1}}&a_{n}\end{array}\right].](wyklady/mo2/mi/mi798.png) |
Przypomnijmy, że każdą macierz symetryczną można sprowadzić
do postaci trójdiagonalnej przez podobieństwa ortogonalne.
W rozdziale 2.1.1 pokazaliśmy jak to zrobić przy pomocy
odbić Householdera. Ale równie dobrze możemy użyć obrotów
Givensa. Rzeczywiście, najpierw wybieramy obroty ![]() dla
dla ![]() tak, aby mnożenie
tak, aby mnożenie
spowodowało wyzerowanie kolejno elementów
![]() . (Pamiętamy o algorytmie Gentlemana!)
Ponieważ mnożenie z prawej strony przez
. (Pamiętamy o algorytmie Gentlemana!)
Ponieważ mnożenie z prawej strony przez ![]() zmienia jedynie
kolumny
zmienia jedynie
kolumny ![]() -gą oraz
-gą oraz ![]() -tą to po operacji
-tą to po operacji
wyzerowane elementy w pierwszej kolumnie się nie zmienią. Dalej
postępujemy indukcyjnie dla kolejnych kolumn, od ![]() -giej do
-giej do
![]() -giej, i ostatecznie dostajemy macierz trójdiagonalną
-giej, i ostatecznie dostajemy macierz trójdiagonalną
![]() , gdzie
, gdzie
przy czym mnożenie z lewej przez ![]() zeruje element
zeruje element
![]() .
.
Oczywiście, wszystkie metody dla macierzy pełnej można stosować również dla macierzy trójdiagonalnej. Jednak ze względu na prostszą strukturę macierzy niektóre metody znacznie się upraszczają. Pokażemy to na przykładzie metody QR z rozdziału 3.2.
W oryginalnej metodzie QR (z przesunięciami lub bez) rozkład
ortogonalno-trójkątny macierzy ![]() dokonuje się przy pomocy
odbić Householdera. Dla macierzy trójdiagonalnej
dokonuje się przy pomocy
odbić Householdera. Dla macierzy trójdiagonalnej ![]() wygodnie jest
użyć do tego celu obrotów Givensa
wygodnie jest
użyć do tego celu obrotów Givensa ![]() zerujących
kolejno elementy
zerujących
kolejno elementy ![]() dla
dla ![]() . Wtedy
. Wtedy
jest macierzą trójkątną górną. Teraz istotne jest, że po wykonaniu drugiego kroku metody QR, czyli mnożenia
otrzymana macierz ![]() pozostaje trójdiagonalna. Rzeczywiście,
skoro
pozostaje trójdiagonalna. Rzeczywiście,
skoro ![]() jest trójkątna górna, a mnożenie z lewej strony
przez
jest trójkątna górna, a mnożenie z lewej strony
przez ![]() kombinuje jedynie wiersze
kombinuje jedynie wiersze ![]() -ty i
-ty i ![]() -szy
to
-szy
to ![]() jest macierzą górną Hessenberga, a ponieważ jest
również symetryczna, to jest trójdiagonalna.
jest macierzą górną Hessenberga, a ponieważ jest
również symetryczna, to jest trójdiagonalna.
Koszt jednego kroku metody QR dla symetrycznej macierzy
trójdiagonalnej ![]() jest więc proporcjonalny do
jest więc proporcjonalny do ![]() .
.
Mamy własność ogólniejszą. W procesie iteracyjnym metody QR
macierz trójdiagonalna pozostaje w każdym kroku trójdiagonalna
niezależnie od zastosowanego algorytmu rozkładu na iloczyn
ortogonalno-trójkątny. Wynika to w szczególności stąd, że,
jak pamiętamy, rozkład taki jest wyznaczony jednoznacznie
z dokładnością do macierzy diagonalnej z elementami ![]() .
(Jako ćwiczenie, można to pokazać bezpośrednio w przypadku
gdy rozkład dokonywany jest przy użyciu odbić Householdera.)
.
(Jako ćwiczenie, można to pokazać bezpośrednio w przypadku
gdy rozkład dokonywany jest przy użyciu odbić Householdera.)
Oczywiście wszystkie pozostałe fakty na temat metody QR pokazane wcześniej dla macierzy pełnych, w szczególności te dotyczące wyboru przesunięcia i szybkości zbieżności, pozostają w mocy gdy macierz jest trójdiagonalna.
4.4. Rozkład według wartości szczególnych (SVD)
Na końcu serii wykładów na temat zadania własnego zajmiemy się znajdowaniem wartości szczególnych danej macierzy, a to dlatego, że zadanie to i metody jego rozwiązania wiążą się ściśle z zadaniem i metodami znajdowania wartości własnych macierzy symetrycznych.
4.4.1. Twierdzenie o rozkładzie
Najpierw przypomnimy twierdzenie o rozkładzie według wartości
szczególnych, czyli SVD (ang. Singular Value Decomposition).
Będziemy zakładać, bez zmniejszenia ogólności, że liczba kolumn
macierzy ![]() nie przekracza liczby jej wierszy, co najczęściej
występuje w praktyce. W przeciwnym przypadku wystarczy zastosować
poniższe twierdzenie dla macierzy transponowanej
nie przekracza liczby jej wierszy, co najczęściej
występuje w praktyce. W przeciwnym przypadku wystarczy zastosować
poniższe twierdzenie dla macierzy transponowanej ![]() .
.
Twierdzenie 4.1
Dla dowolnej macierzy ![]() , gdzie
, gdzie ![]() , istnieją macierze
ortogonalne
, istnieją macierze
ortogonalne ![]() i
i ![]() takie, że
takie, że
gdzie ![]() jest macierzą diagonalną,
jest macierzą diagonalną,
![]() ,
a
,
a ![]() jest rzędem macierzy
jest rzędem macierzy ![]() .
.
Dowód
Ponieważ macierz ![]() jest symetryczna i nieujemnie określona to
istnieje baza ortonormalna
jest symetryczna i nieujemnie określona to
istnieje baza ortonormalna ![]() jej wektorów własnych,
a odpowiadające jej wartości własne są nieujemne
(patrz twierdzenia 1.1).
Oznaczmy te wartości własne odpowiednio przez
jej wektorów własnych,
a odpowiadające jej wartości własne są nieujemne
(patrz twierdzenia 1.1).
Oznaczmy te wartości własne odpowiednio przez ![]() ,
,
przy czym ![]() . Zauważmy, że
. Zauważmy, że
To oznacza, że wektory ![]() ,
, ![]() ,
tworzą układ ortonormalny i można go uzupełnić wektorami
,
tworzą układ ortonormalny i można go uzupełnić wektorami
![]() do bazy ortonormalnej w
do bazy ortonormalnej w ![]() .
.
Zdefiniujmy teraz macierze ortogonalne
Wtedy, oznaczając ![]() ,
mamy
,
mamy
albo, równoważnie, ![]() .
.
Wielkości ![]() ,
, ![]() , to właśnie wartości szczególne
macierzy
, to właśnie wartości szczególne
macierzy ![]() . Są one wyznaczone jednoznacznie. Rzeczywiście, jeśli mamy dwa
rozkłady,
. Są one wyznaczone jednoznacznie. Rzeczywiście, jeśli mamy dwa
rozkłady,
![]() , to
, to
Porównując wyrazy diagonalne po obu stronach powyższej równości
dostajemy ![]() dla wszsytkich
dla wszsytkich ![]() .
.
Zanotujmy jeszcze, że mając rozkład SVD można np. łatwo rozwiązać liniowe
zadanie najmniejszych kwadratów, tzn. znaleźć wektor ![]() minimalizujący
minimalizujący
![]() po wszystkich
po wszystkich ![]() . (Jeśli istnieje wiele
takich wektorów to bierzemy ten o najmniejszej normie.) Mamy bowiem
. (Jeśli istnieje wiele
takich wektorów to bierzemy ten o najmniejszej normie.) Mamy bowiem
![]() ,
, ![]() . Stąd
. Stąd ![]() , gdzie
, gdzie
4.4.2. Dlaczego nie pomnożyć  ?
?
Z dowodu twierdzenia 4.1 wynika, że ![]() są wartościami własnymi macierzy symetrycznej i nieujemnie określonej
są wartościami własnymi macierzy symetrycznej i nieujemnie określonej ![]() ,
a kolumny macierzy ortogonalnej
,
a kolumny macierzy ortogonalnej ![]() tworzą odpowiednio bazę ortonormalną
w
tworzą odpowiednio bazę ortonormalną
w ![]() wektorów własnych tej macierzy. Podobnie,
wektorów własnych tej macierzy. Podobnie,
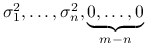 są wartościami własnymi
są wartościami własnymi ![]() , a kolumny
, a kolumny ![]() tworzą bazę ortonormalną
w
tworzą bazę ortonormalną
w ![]() wektorów własnych. Wydaje się więc, że wartości szczególne
(i w razie potrzeby cały rozkład SVD) można łatwo wyznaczyć wykonując
najpierw mnożenie
wektorów własnych. Wydaje się więc, że wartości szczególne
(i w razie potrzeby cały rozkład SVD) można łatwo wyznaczyć wykonując
najpierw mnożenie ![]() lub
lub ![]() , a następnie aplikując
do macierzy
, a następnie aplikując
do macierzy ![]() jedną z rozpatrzonych wcześniej metod dla zadania własnego.
Należy jednak przestrzec przed takim mechanicznym działaniem.
jedną z rozpatrzonych wcześniej metod dla zadania własnego.
Należy jednak przestrzec przed takim mechanicznym działaniem.
Przykład 4.1
Niech ![]() Dla ,,małych”
Dla ,,małych” ![]() wartości szczególne tej macierzy są bliskie
wartości szczególne tej macierzy są bliskie
![]() i
i ![]() . Jeśli
. Jeśli ![]() jest na tyle małe, że
jest na tyle małe, że
![]() jest w arytmetyce fl reprezentowane przez
jest w arytmetyce fl reprezentowane przez ![]() to macierz
to macierz
![]() jest reprezentowana przez macierz
jest reprezentowana przez macierz
![]() ,
która jest już osobliwa - jej druga wartość szczególna jest zerowa.
,
która jest już osobliwa - jej druga wartość szczególna jest zerowa.
Z uwagi na możliwą zmianę rzędu macierzy, jak w przytoczonym przykładzie,
stosuje się nieco zmodyfikowane algorytmy znajdowania wartości własnych,
które unikają jawnych mnożeń ![]() lub
lub ![]() . Pokażemy to najpierw,
nie wdając się w szczegóły, na przykładzie metody Jacobiego
z rozdziału 4.2.
. Pokażemy to najpierw,
nie wdając się w szczegóły, na przykładzie metody Jacobiego
z rozdziału 4.2.
Przypomnijmy, że metoda Jacobiego zastosowana bezpośrednio do macierzy
![]() konstruuje ciąg macierzy podobnych
konstruuje ciąg macierzy podobnych
![]() , gdzie
, gdzie
![]() , a
, a ![]() jest tak
dobranym obrotem Givensa, aby wyzerować element
jest tak
dobranym obrotem Givensa, aby wyzerować element ![]() i jednocześnie, wobec
symetrii, także
i jednocześnie, wobec
symetrii, także ![]() . Oznaczmy
. Oznaczmy ![]() i
i ![]() dla
dla
![]() . Wtedy
. Wtedy ![]() . Pomysł polega na tym, aby zamiast obliczać
jawnie
. Pomysł polega na tym, aby zamiast obliczać
jawnie ![]() , w kolejnych krokach
obliczać i pamiętać jedynie
, w kolejnych krokach
obliczać i pamiętać jedynie ![]() . Jest to możliwe, bowiem
wyznaczenie rotacji
. Jest to możliwe, bowiem
wyznaczenie rotacji ![]() wymaga jedynie znajomości elementów
wymaga jedynie znajomości elementów
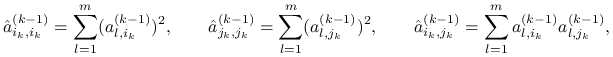 |
które można obliczyć korzystając z powyższych wzorów.
4.4.3. SVD dla macierzy dwudiagonalnych
W tym podrozdziale pokażemy algorytm, który można traktować jako wariant
metody QR zastosowanej do macierzy ![]() . Zanim jednak przejdziemy do samego
algorytmu, poczynimy kilka pomocniczych uwag teoretycznych.
. Zanim jednak przejdziemy do samego
algorytmu, poczynimy kilka pomocniczych uwag teoretycznych.
Niech ![]() będzie macierzą symetryczną i dodanio okteśloną,
będzie macierzą symetryczną i dodanio okteśloną, ![]() .
Rozpatrzmy proces iteracyjny, nazwijmy go LR, który startuje z macierzy
.
Rozpatrzmy proces iteracyjny, nazwijmy go LR, który startuje z macierzy ![]() i w kolejnych krokach
i w kolejnych krokach ![]()
(i) wybiera przesunięcie
 , mniejsze od najmniejszej wartości
własnej
, mniejsze od najmniejszej wartości
własnej  (np.
(np. 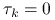 ),
),(ii) dokonuje rozkładu Banachiewicza-Cholesky'ego
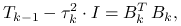
gdzie
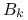 jest macierzą trójkątną górną
z dodatnimi elementami na głównej przekątnej,
jest macierzą trójkątną górną
z dodatnimi elementami na głównej przekątnej,
(iii) produkuje
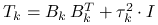 .
.
(Przypomnijmy, że rozkładu Banachiewicza-Cholesky'ego dokonujemy zmodyfikowanym
algorytmem eliminacji Gaussa.) Oczywiście, macierze ![]() są do siebie podobne, bo
są do siebie podobne, bo
Zachodzi ciekawsza własność.
Lemat 4.1
Dwa kroki iteracji LR z tym samym przesunięciem ![]() są równoważne jednemu
krokowi iteracji QR z przesunięciem
są równoważne jednemu
krokowi iteracji QR z przesunięciem ![]() .
.
Dowód
Bez zmniejszenia ogólności przyjmijmy, że ![]() i
i ![]() . Z jednej
strony, z rozkładu QR mamy
. Z jednej
strony, z rozkładu QR mamy ![]() , gdzie
elementy na głównej przekątnej macierzy
, gdzie
elementy na głównej przekątnej macierzy ![]() są dodatnie, a z drugiej z rozkładu LR
są dodatnie, a z drugiej z rozkładu LR
Wobec jednoznaczności rozkładu Banachiewicza-Cholesky'ego mamy więc ![]() .
Stąd macierz powstała w wyniku jednego kroku iteracji QR wynosi
.
Stąd macierz powstała w wyniku jednego kroku iteracji QR wynosi
jak w tezie lematu.
∎Powyższy lemat pokazuje, że rozważania teoretyczne dotyczące iteracji QR można przenieść na iteracje LR. Dlatego dalej nie będziemy się już zajmować analizą teoretyczną LR, a przejdziemy do opisu algorytmu te iteracje wykorzystującego.
Zakładamy, że ![]() jest kolumnowo regularna, czyli
jest kolumnowo regularna, czyli ![]() ,
oraz dwudiagonalna. Dokładniej,
,
oraz dwudiagonalna. Dokładniej,
![]() dla
dla ![]() i dla
i dla ![]() ,
,
![A=\left[\begin{array}[]{cccc}a_{1}&b_{1}&&\\
&a_{2}&\ddots&\\
&&\ddots&b_{{n-1}}\\
&&&a_{n}\\
&&&\\
&&&\end{array}\right].](wyklady/mo2/mi/mi915.png) |
Oczywiście, wobec kolumnowej regularności macierzy mamy ![]() .
Założenie o dwudiagonalności wydaje się mocno ograniczające. W istocie jednak
tak nie jest, bo każdą macierz można sprowadzić do takiej postaci nie zmieniając
jej wartości szczególnych i kontrolując odpowiednie wektory własne, co
pokażemy na samym końcu.
.
Założenie o dwudiagonalności wydaje się mocno ograniczające. W istocie jednak
tak nie jest, bo każdą macierz można sprowadzić do takiej postaci nie zmieniając
jej wartości szczególnych i kontrolując odpowiednie wektory własne, co
pokażemy na samym końcu.
Algorytm działa podobnie jak iteracje LR z przesunięciami, ale zamiast tworzyć
jawnie macierze ![]() , podobne do
, podobne do ![]() , pracuje bezpośrednio na macierzach
, pracuje bezpośrednio na macierzach ![]() .
Przyjmujemy
.
Przyjmujemy ![]() , gdzie
, gdzie ![]() jest macierzą diagonalną z elementami
na głównej przekątnej
jest macierzą diagonalną z elementami
na głównej przekątnej ![]() ,
, ![]() . Wtedy
. Wtedy ![]() jest macierzą dwudiagonalną z dodatnimi elementami na głównej przekątnej oraz
jest macierzą dwudiagonalną z dodatnimi elementami na głównej przekątnej oraz
jest macierzą trójdiagonalną. Zobaczmy teraz jak mając macierz dwudiagonalną
![]() możemy skonstruować
możemy skonstruować ![]() . Ponieważ
. Ponieważ ![]() jest trójdiagonalna to
jest trójdiagonalna to
![]() musi być dwudiagonalna. (W szczególności, wyniknie to również
z dalszych rachunków.) Dla uproszczenia zapisu, oznaczmy elementy przekątniowe
macierzy
musi być dwudiagonalna. (W szczególności, wyniknie to również
z dalszych rachunków.) Dla uproszczenia zapisu, oznaczmy elementy przekątniowe
macierzy ![]() i
i ![]() odpowiednio przez
odpowiednio przez ![]() i
i ![]() ,
, ![]() ,
a elementy nad główną przekątną przez
,
a elementy nad główną przekątną przez ![]() i
i ![]() ,
, ![]() .
Przyjmijmy dodatkowo
.
Przyjmijmy dodatkowo ![]() . Macierze
. Macierze ![]() i
i ![]() związane są równaniem
związane są równaniem
Porównując wyrazy przekątniowe po obu stronach tej równości otrzymujemy
a porównując wyrazy nad przekątną
Stąd, podstawiając ![]() , mamy następujące wzory
na
, mamy następujące wzory
na ![]() i
i ![]() . Dla
. Dla ![]() obliczamy
obliczamy
i na końcu ![]() .
.
Ponieważ obliczanie pierwiastków jest stosunkowo kosztowne, wzory te
opłaca się zmodyfikować tak, aby nie obliczać pierwiastków w każdej
iteracji, a jedynie na końcu całego procesu iteracyjnego. Można to
osiągnąć pracując na kwadratach ![]() i
i ![]() . Rzeczywiście, wprowadzając
zmienne
. Rzeczywiście, wprowadzając
zmienne ![]() i
i ![]() , otrzymujemy następującą procedurę dla
jednego kroku iteracyjnego:
, otrzymujemy następującą procedurę dla
jednego kroku iteracyjnego:
| . | begin | ||
| . | . | for |
|
| . | . | begin | |
| . | . | . | |
| . | . | . | |
| . | . | end; | |
| . | . | ||
| . | end; |
A co jeśli ![]() nie jest dwudiagonalna? Wtedy trzeba ją wstępnie
przekształcić do postaci dwudiagonalnej nie zmieniając wartości szczególnych.
W tym celu możemy użyć np. odbić Householdera. Najpierw zerujemy wyrazy
w pierwszej kolumnie, oprócz wyrazu diagonalnego, poprzez pomnożenie macierzy
nie jest dwudiagonalna? Wtedy trzeba ją wstępnie
przekształcić do postaci dwudiagonalnej nie zmieniając wartości szczególnych.
W tym celu możemy użyć np. odbić Householdera. Najpierw zerujemy wyrazy
w pierwszej kolumnie, oprócz wyrazu diagonalnego, poprzez pomnożenie macierzy
![]() z lewej strony przez odbicie
z lewej strony przez odbicie ![]() przekształcające pierwszą
kolumnę
przekształcające pierwszą
kolumnę ![]() na kierunek
na kierunek ![]() . Oznaczmy
. Oznaczmy ![]() .
Następnie wybieramy odbicie
.
Następnie wybieramy odbicie ![]() tak, aby przekształcało
wektor
tak, aby przekształcało
wektor ![]() na kierunek
na kierunek ![]() i mnożymy
i mnożymy ![]() z prawej przez
z prawej przez
![H^{T}_{{R,1}}=\left[\begin{array}[]{cc}1&\vec{0}^{T}\\
\vec{0}&\tilde{H}^{T}_{{R,1}}\end{array}\right]\in\mathbb{R}^{{n,n}}](wyklady/mo2/mi/mi878.png) . Ponieważ to mnożenie nie zmienia pierwszej
kolumny
. Ponieważ to mnożenie nie zmienia pierwszej
kolumny ![]() , w powstałej macierzy
, w powstałej macierzy
![]() elementy w pierwszej kolumnie i w pierwszym wierszu,
poza
elementy w pierwszej kolumnie i w pierwszym wierszu,
poza ![]() i
i ![]() , są wyzerowane. Dalej postępujemy indukcyjnie zerując
na przemian odpowiednie elementy w kolumnach i wierszach. Ostatecznie, po
, są wyzerowane. Dalej postępujemy indukcyjnie zerując
na przemian odpowiednie elementy w kolumnach i wierszach. Ostatecznie, po
![]() krokach otrzymujemy macierz
krokach otrzymujemy macierz
która jest już dwudiagonalna. Jeśli teraz ![]() to
to
![]() , a więc
, a więc ![]() i
i ![]() mają te same
wartości szczególne. Ponadto,
mają te same
wartości szczególne. Ponadto,
Zanotujmy jeszcze, że dowolną macierz można sprowadzić w podobny sposób
do postaci dwudiagonalnej przy pomocy obrotów Givensa. Zarówno w przypadku
zastosowania obrotów Givensa jak i odbić Householdera koszt jest
proporcjonalny do ![]() .
.




